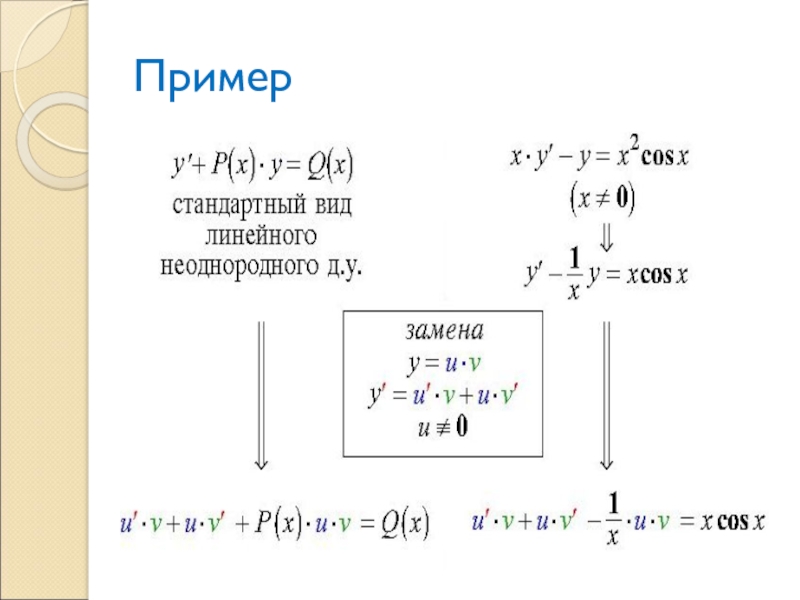
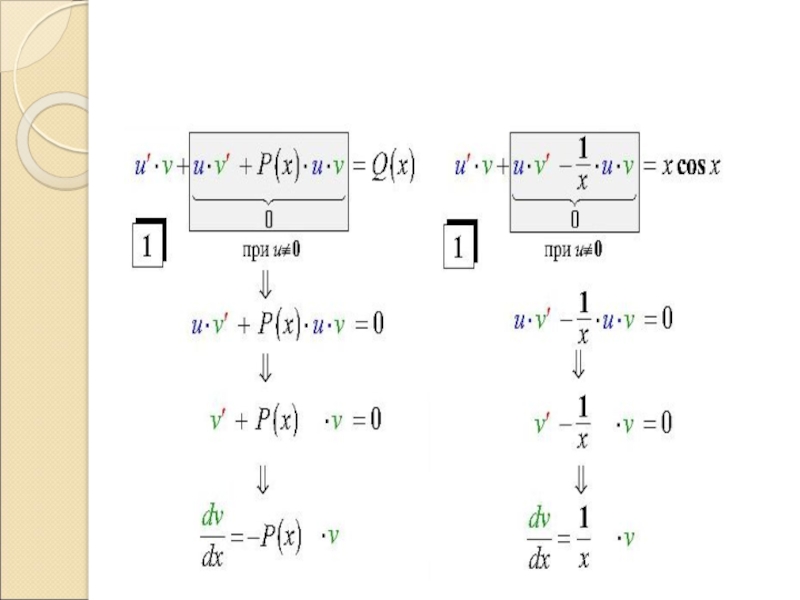
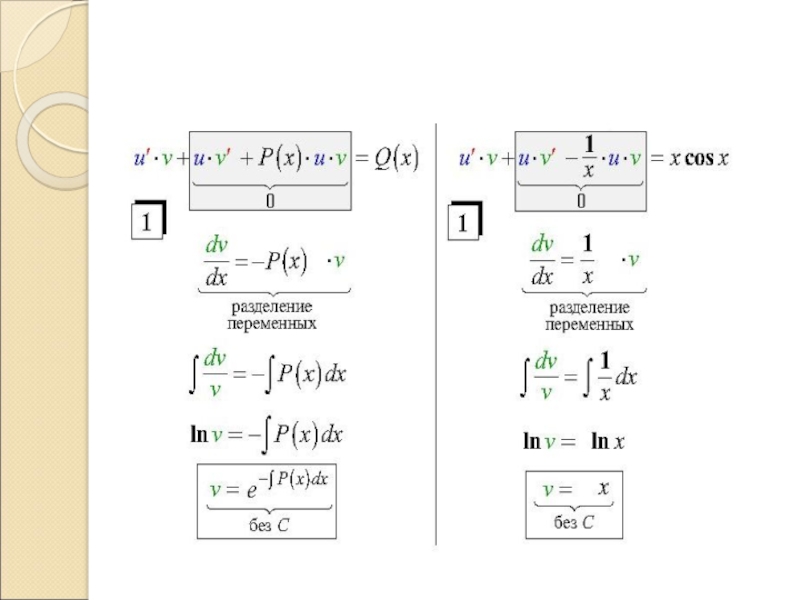
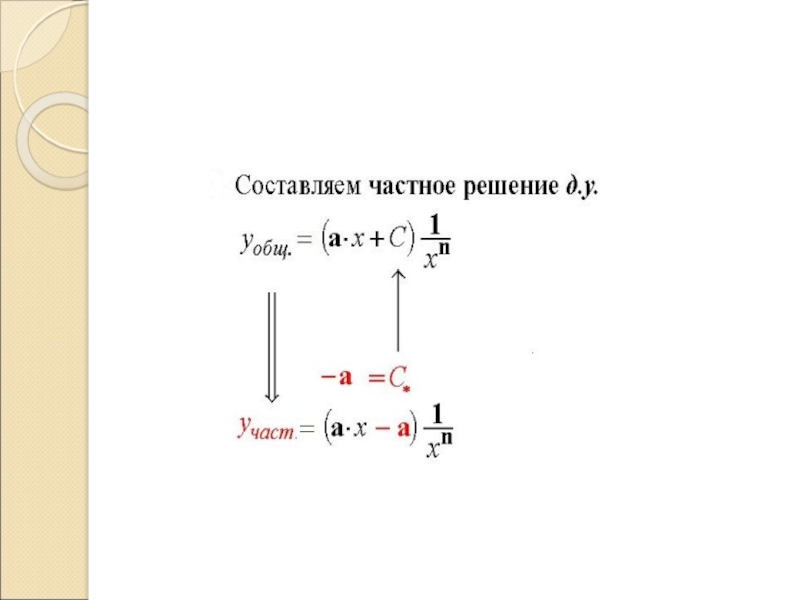
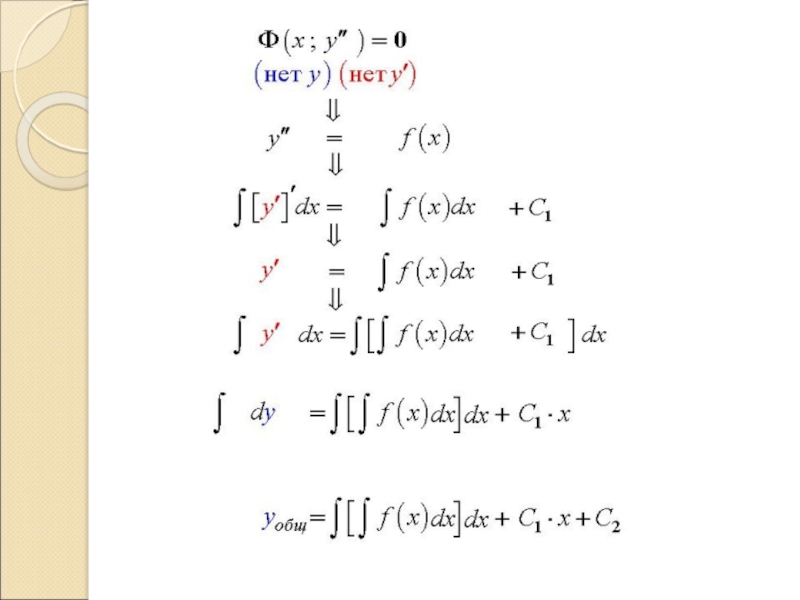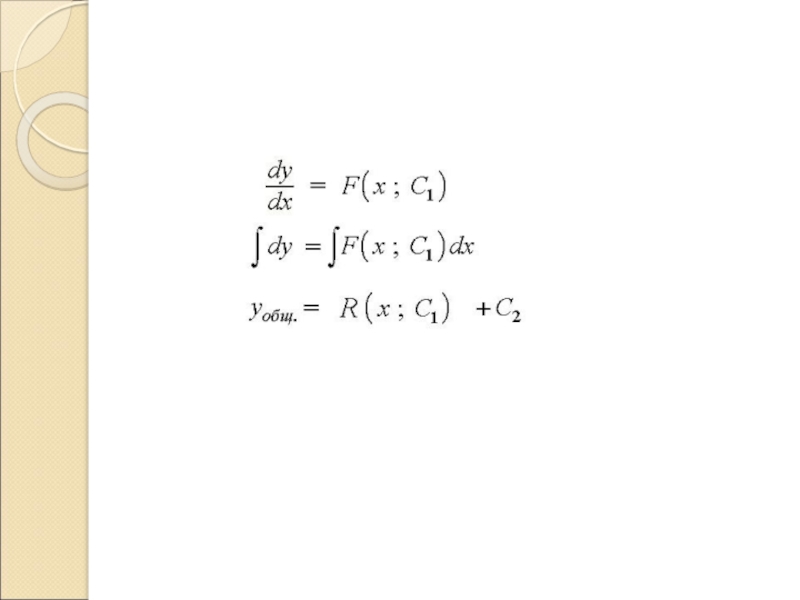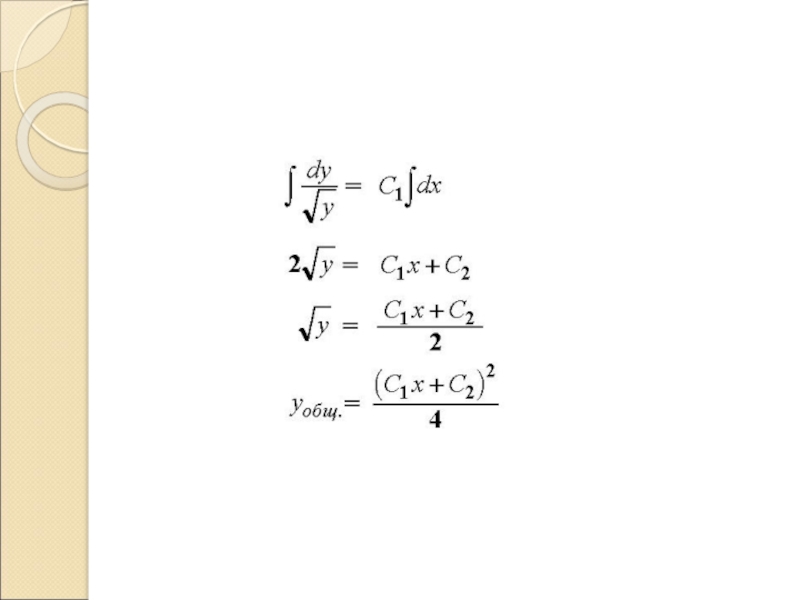Слайд 1Лекция
Линейные дифференциальные уравнения 1- го порядка
Слайд 2 Линейные уравнения первого порядка
Определение Линейное дифференциальное уравнение первого
порядка - ДУ 1-го порядка, линейное относительно неизвестной функции y
и ее производной y .
В общем случае линейное уравнение 1-го порядка можно записать в виде
y + p(x) y = f(x) , где p(x) , f(x) – заданные непрерывные функции.
Определение Если f(x) ≡ 0 , то линейное уравнение
y + p(x) y = 0
называется однородным.
В противном случае уравнение называется неоднородным.
Слайд 3Линейное однородное уравнение
y + p(x) y = 0
является уравнением с разделяющимися переменными.
Его общее решение:
Слайд 15Метод вариации постоянной
(метод Лагранжа)
y + p(x) y = f(x)
1)Интегрируем однородное уравнение
y + p(x) y = 0,
Соответствующее данному неоднородному уравнению.
Его общее решение имеет вид :
2) Полагаем, что
решение неоднородного уравнения
Функцию C(x) найдем, подставив y и y в исходное неоднородное уравнение .
Слайд 16Получим:
Таким образом,
общее решение линейного неоднородного уравнения имеет вид:
Замечания.
Раскроем скобки
первое слагаемое– общее решение линейного однородного
уравнения,
второе – частное решение линейного неоднородного уравнения (получается из общего решения при C = 0).
Слайд 17Уравнения в полных дифференциалах
Определение Уравнение M(x , y)dx + N(x , y)dy = 0
называется уравнением в полных дифференциалах,
если его левая часть является полным дифференциалом некоторой функции u(x , y) ,
т.е. если
M(x , y)dx + N(x , y)dy = du(x , y) .
Общий интеграл уравнения в полных дифференциалах имеет вид u(x , y) = C .
Задачи:
1) научиться определять, когда выражение
M(x , y)dx + N(x , y)dy
является полным дифференциалом;
2) научиться находить функцию u(x , y), зная ее полный дифференциал.
Слайд 18ТЕОРЕМА
Пусть функции M(x , y) , N(x , y) определены и непрерывны в
области D и имеют в ней непрерывные частные производные
Для
того чтобы выражение M(x , y)dx + N(x , y)dy
представляло собой полный дифференциал некоторой функции u(x , y) , необходимо и достаточно, чтобы во всех точках области D выполнялось условие
Слайд 19Способы нахождения функции u(x , y):
1) используя одну из следующих формул:
где (x0 ,y0)
– любая точка области D непрерывности функций M(x , y), N(x , y).
Слайд 20 Метод интегрируемых комбинаций.
Суть метода интегрируемых комбинаций: выделить в
M(x , y)dx + N(x , y)dy
выражения, являющиеся дифференциалами известных функций («интегрируемые комбинации») и привести
его таким образом к виду du(x , y) .
ПРИМЕРЫ интегрируемых комбинаций:
Слайд 21Интегрирующий множитель
Определение Функция m(x,y) называется интегрирующим множителем
уравнения
M(x , y)dx + N(x , y)dy = 0,
если после его умножения на m(x,y)
левая часть уравнения становится полным дифференциалом некоторой функции.
Пусть функции M(x , y) , N(x , y) определены и непрерывны в области D плоскости xOy и имеют в ней непрерывные частные производные
Слайд 22ТЕОРЕМА (о существовании интегрирующего множителя вида m(x) или m(y)).
Пусть
1) Если
= (x), то уравнение имеет интегрирующий множитель m(x), который является решением
уравнения
2) Если = (y), то уравнение имеет интегрирующий множитель m(y), который является решением уравнения
Слайд 23Уравнение Бернулли
Определение Уравнение вида
где
.
- любое вещественное число, называется
уравнением Бернулли
Замечание Будем считать,
так как в этих случаях уравнение
Бернулли вырождается в линейное
отлично от нуля и единицы,
Слайд 24Уравнение Бернулли всегда может быть сведено к линейному уравнению
заменой
деля
уравнение на
Замечание Особым решением
может быть лишь при
Если
частное решение,
особое решение.
Слайд 252) Решив получившееся после замены линейное уравнение методом Бернулли, получим:
z = u(x) v(x) ,
Таким образом,
решение уравнения Бернулли можно сразу искать в виде произведения двух
функций методом Бернулли, не приводя предварительно к линейному уравнению.
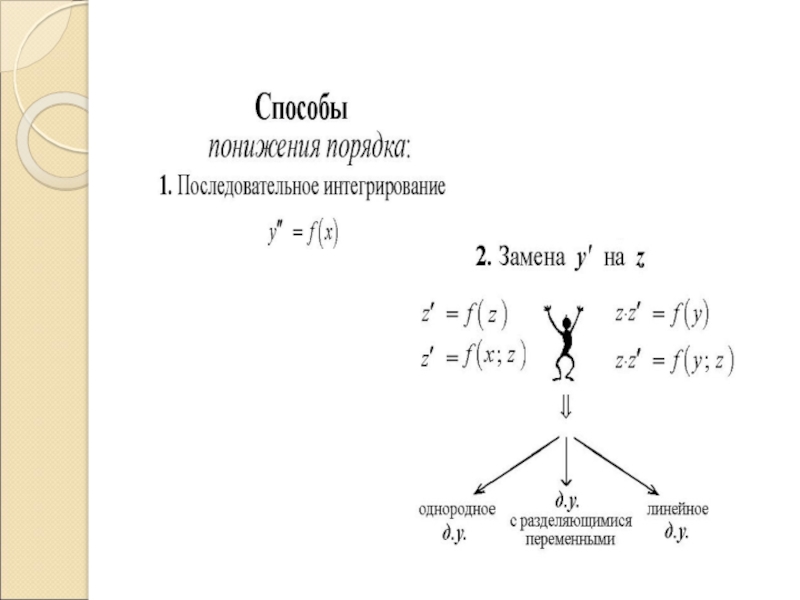
Слайд 26Дифференциальные уравнения высшего порядка
Определение Сведение уравнение более высокого порядка к
уравнению порядком ниже называется понижением порядка.
Рассмотрим некоторые случаи, в
которых данное дифференциальное уравнений высшего порядка может быть упрощено понижением его порядка.
Слайд 27Определение Дифференциальными уравнениями высшего порядка называют уравнения порядка выше первого.
В общем случае ДУ высшего порядка имеет вид
F(x, y , y , y , y , … , y(n)) = 0 ,
где n > 1 .
Замечание Функция
F может и не зависеть от некоторых из аргументов x, y , y , … , y(n–1) .
Определение ДУ высшего порядка, которое можно записать в виде:
y(n) = f(x, y , y , y , … , y(n–1)) ,
называют уравнением, разрешенным относительно старшей производной.
Слайд 28Дифференциальные уравнения 1-го порядка, не разрешенные относительно производной
ДУ 1-го
порядка, разрешенное относительно производной – уравнение, которое можно записать в
виде
y = f(x,y).
В общем случае ДУ 1-го порядка имеет вид:
F(x, y, y ) = 0 .
Если из уравнения F(x, y, y ) = 0 нельзя выразить y , то уравнение называют не разрешенным относительно производной.
Слайд 29 Уравнения, разрешаемые относительно y неоднозначно
Пусть F(x, y, y ) = 0 таково, что
его можно разрешить относительно y неоднозначно.
Т.е. уравнение F(x, y, y ) = 0 эквивалентно
k различным уравнениям
y = f1(x,y) , y = f2(x,y) ,
y = f3(x,y) , … , y = fk(x,y) .
Предположим, что для каждого из уравнений найден общий интеграл:
Φ1(x , y , C) = 0 , Φ2(x , y , C) = 0 , ….,
Φk(x , y , C) = 0 .
Совокупность общих интегралов называется общим интегралом уравнения разрешаемого относительно y неоднозначно.
Слайд 30Замечания
Если уравнение
F(x, y, y ) = 0
разрешается относительно y неоднозначно, то через каждую
точку M0(x0 ,y0) области, будет проходить в общем случае k интегральных
кривых.
Однако условие единственности для этой точки будет считаться нарушенным только в том случае, когда хотя бы две кривые в точке M0 будут иметь общую касательную.
Слайд 31ПРИМЕР Найти общий интеграл уравнения
(y )2 – 4 x2 = 0.
Найти
решение, удовлетворяющее условию
а) y(1) = 1 , б) y(0) = 0 .
Слайд 32ДУ порядка n имеет множество решений (интегралов).
Чтобы выбрать одно
из них, задают n условий, которым должно удовлетворять искомое решение.
Обычно, задают значение искомой функции и всех ее производных до порядка n – 1 включительно при некотором значении аргумента x = x0 :
y(x0)=y0 ,y (x0) =y01,y (x0)= y02 ,
…, y(n–1)(x0)=y0n–1 .
Совокупность этих условий называется начальными условиями для дифференциального уравнения n-го порядка.
Определение Нахождение решения уравнения, удовлетворяющего заданным начальным условиям , называется решением задачи Коши для этого уравнения.
Слайд 33Замечание Единственность решения задачи Коши для уравнения n-го порядка (n > 1)
НЕ ОЗНАЧАЕТ, что через данную точку M0(x0 ,y0) плоскости xOy проходит
одна интегральная кривая y = (x).
Кривых через точку M0 проходит множество, а единственность означает, что они различаются набором значений y (x0) , y (x0) , …, y(n–1)(x0) .
Из теоремы 1
1) ДУ имеет множество решений.
2) Совокупность решений зависит от n произвольных постоянных.
Слайд 34ОПРЕДЕЛЕНИЕ. Общим решением дифференциального уравнения
y(n) = f(x, y, y , y , … , y(n–1))
в
области D существования и единственности решения задачи Коши называется функция
y = (x , C1 , C2 , … , Cn) ,
зависящая от x и n произвольных постоянных C1 , C2 , … , Cn , которая удовлетворяет следующим двум условиям:
1) при любых допустимых значениях C1 , C2 , … , Cn она удовлетворяет уравнению
2) каковы бы ни были начальные условия
y(x0) = y0, y (x0) = y01, y (x0) = y02, … , y(n–1)(x0) = y0n– (где (x0,y0,y01,y02,…,y0n–1)D), можно найти единственный набор значений C1 = C01 , C2 = C02 , … , Cn = C0n такой, что функция y = (x , C01 , C02 , … , C0n) удовлетворяет заданным начальным условиям.
Слайд 36Уравнение Φ(x , y , C1 , C2 , … , Cn) = 0 , задающее общее решение в неявном виде, называется общим
интегралом уравнения.
С геометрической точки зрения общее решение (общий интеграл) дифференциального
уравнения представляет собой семейство интегральных кривых, зависящих от n параметров.
Решение , в каждой точке которого выполняется условие единственности, называется частным.
Любое решение , получающееся из общего решения (интеграла) при конкретных значениях постоянных Ci (включая Ci = ), является частным.
Решение , в каждой точке которого нарушено условие единственности, называется особым.
Особое решение, не входит в общее решение дифференциального уравнения.
Слайд 37ТЕОРЕМА (Коши).
Пусть для уравнения
y(n) = f(x, y , y , y , … , y(n–1))
выполняются два условия:
1)
функция f(x, y , y , y , … , y(n–1)) непрерывна как функция (n + 1)-ой переменной x, y , y , y , … , y(n–1)
2)
функция f(x, y , y , y , … , y(n–1)) имеет в этой области D ограниченные частные производные по переменным y , y , y , … , y(n–1) .
Тогда для любой точки (x0 ,y0 ,y01 ,y02 , … , y0n–1)D существует, и притом единственное, решение y = (x), определенное в некотором интервале, содержащем точку x0 , и удовлетворяющее начальным условиям
(x0) = y0 , (x0) = y01 ,
(x0) = y02 , … , (n–)(x0) = y0n–1 .
Слайд 38Дифференциальные уравнения
2 порядка
Слайд 41Дифференциальные уравнения n-го порядка
- легко интегрируется в квадратурах.
Решение уравнения
находится кратным интегрированием.
интегрируя , получим
Простейшее дифференциальное уравнение n-го порядка –
уравнение вида
общее решение
Слайд 42Пример
Найти общее решение уравнения
и частное решение, удовлетворяющее краевым условиям:
Решение
общее решение
частное решение
Слайд 43Дифференциальные уравнения ,
допускающие понижение порядка
Уравнения, не содержащие искомой функции
Функция
- общее решение,
особых решений нет.
Слайд 50Уравнения, не содержащие независимой переменной
Обратимся к перевернутому уравнению
Разделим
на
, интегрируя, получим
общее решение
Рассмотрим
Если оно имеет
решение вида
то прямая
решение, частное или особое
Слайд 52Уравнения, не содержащие искомой функции
Пусть ДУ имеет вид
F(x, y ) = 0 ,
Возможны 2 случая:
1)
разрешимо относительно y неоднозначно;
2)неразрешимо относительно y , но допускает параметрическое представление,
т.е. может быть заменено двумя урав
нениями вида
x = (t) , y = (t) .
Тогда решения уравнения могут быть найдены в параметрическом виде.
Имеем: dy = y dx , x = (t) dx = dt ,
dy = (t) dt ,
Слайд 53Таким образом, интегральные кривые уравнения имеют параметрические уравнения:
Замечания
1) Общий
интеграл уравнения получается исключением параметра t из системы (если это
возможно).
2) Если уравнение можно разрешить относительно x, т.е. записать в виде x = (y ) , то в качестве параметра удобно брать t = y .
Тогда общий интеграл уравнения
Слайд 56 Уравнения, содержащее только производную
Пусть ДУ имеет вид
F(y ) = 0 .
Тогда y не должна зависеть от x
и y, т.е. быть постоянной.
Пусть y = ki удовлетворяет уравнению F(y ) = 0.
Тогда y = ki x + C ,
Общий интеграл уравнения будет иметь вид
Слайд 59 Уравнение Лагранжа
Уравнение
F(x, y, y ) = 0
называется уравнением Лагранжа, если оно
является линейным относительно x и y, т.е. имеет вид: F1(y ) x + F2(y ) y = G(y ) .
Так как
F2(y ) 0 (иначе это будет неполное уравнение), то уравнение Лагранжа можно записать в виде
y = x (y ) + (y ) . Общее решение уравнения Лагранжа можно найти в параметрическом виде.
Если (y ) ≢ y , то общее решение уравнения будет иметь вид:
Слайд 60 Уравнение Клеро
Пусть в уравнении Лагранжа (y ) ≡ y .
В этом
случае, уравнение называют уравнением Клеро.
Уравнение F(x, y, y ) = 0 называется уравнением Клеро,
если оно может быть записано в виде
y = x y + (y ) .
Общее решение уравнения Клеро имеет вид:
y = x C + (C) .
Кроме того, если (t) const , то уравнение Клеро имеет особое решение