Слайд 1Лекция 2. Линейное программирование
Денисова С.Т.
Старший преподаватель
кафедры ММиМЭ
Слайд 2План:
1 Пример задачи линейное программирования
2 Графический способ решения задачи ЛП.
3
Виды задач линейное программирования. Свойства задачи ЛП.
4 Симплексный метод решения
задачи ЛП. Пример решения симплексным методом.
5 Метод искусственного базиса. Вспомогательная задача
Слайд 3Задача ЛП
Для изготовления 2-х видов продукции P1 и P2 используется
3 вида ресурсов R1, R2, R3. Запасы ресурсов, нормы их
использования и прибыль от реализации единицы продукции приведены в таблице. Найти план производства продукции, которой бы при заданных условиях обеспечивал наибольшую прибыль.
Слайд 4Экономико-математическая модель:
X1- количество продукции вида P1
X2- количество продукции вида
P2
f(x1 ,x2)=15 x1 + 12 x2 max
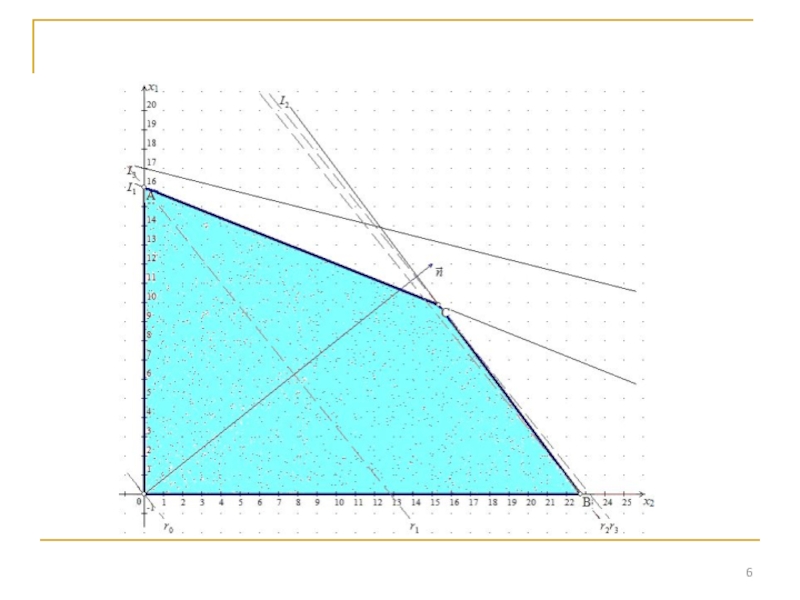
Слайд 5Решение задачи ЛП графическим способом:
Строим многоугольник решений системы ограничений.
L1)
2x1+5x2=80; x2= 16 - 0,4x1; построим прямую по точкам
(0;16), (5;14)
x2= 16 - 0,4x1 - граница множества 2x1+5x2≤80
L2) 4x1+3x2=90; x2= 30 – 4/3 x1; (15;10), (18;22)
L3) x1+4x2=68; x2= 17 –1/4 x1; (0;17), (8;15)
Найдём координаты точки С – точки пересечения 1 и 2 прямой: 16 - 0,4x1= 30 – 4/3 x1 ; -2/5 x1+ 4/3 x1 =30-16
14/15 x1 = 14; x1 = 15; x2= 16-2/5*15=10; C(15;10)
Вектор целевой функции n=(15;12);
Линия уровня f(x1 , x2 )=0 перпендикулярна вектору n
Слайд 7Ответ: Точка max – точка С(15;12); fmax=369.
Для решения симплексным
методом приведём симметричную задачу к каноническому виду, добавив в ограничения
дополнительные переменные:
Слайд 8
ЗЛП и способы её решения
F=c1x1+c2x2+…+cnxn+c0→min(max). При этом переменные должны удовлетворять
ограничениям:
а11х1+ а12х2+…+а1nхn≤b1
…………………………
аm1х1+ аm2х2+…+amnxn≤bm
аm+11х1+ аm+12х2+…+аm+1nхn≥bm+1
…………………………
аk1х1+ аk2х2+…+аknхn≥bk
аk1+1х1+ аk+12х2+…+аk+1nхn=bk+1
………………………….
аp1х1+аp2х2+…+аpnхn=bp
x1,x2,…,хn ≥0.
Слайд 9Виды задач ЛП: 1)Общая задача ЛП:
Слайд 10Формы записи основной (канонического вида) задачи:
Mатричная С=(c1,c2…cn,c0).
F=CX→ max
AX=B, X≥0
Векторная форма записи:
F=CX→ max
A1x1+A2x2+…+Anxn=B, Х≥0. С=(с1,с2,.. cn); XT=(x1,x2,.xn)
Слайд 11Свойства задачи ЛП
Определение. Множество точек D – точек n-мерного евклидова
пространства будем называть выпуклым, если оно вместе с любыми своими
двумя точками содержит их произвольную линейную комбинацию.
Точка Х является выпуклой линейной комбинацией точек Х1=(x11, x21, … xn1)D, Х2=(x12, x22, … xn2)D , для любого >0,
X= α1X1+(1-α)X2 D
1. Допустимая область ЗЛП выпукла, если она не пуста.
2. Если допустимая область имеет вершины и ЗЛП имеет решение, то оно достигается по крайней мере в одной из вершин.
3. Множество решений ЗЛП выпукло.
Слайд 12Свойства задачи ЛП
4. Если допустимая область ограничена, то ЗЛП имеет
оптимальное решение.
5.Необходимым и достаточным условием существования решения ЗЛП на максимум
(минимум) является ограниченность целевой функции сверху (снизу) в допустимой области.
Множество всех допустимых решений ЗЛП является выпуклым, которое будем называть многогранником решений.
Слайд 13Свойства задачи ЛП
6.Если ЗЛП имеет оптимальное решение, то линейная функция
F принимает максимальное (минимальное) значение в одной из угловых точек
многогранника решений. Если линейная функция принимает максимальное значение более чем в одной угловой точке, то она принимает его в произвольной точке, являющейся выпуклой линейной комбинацией этих точек.
Слайд 14Симплексный метод решения задачи ЛП
Для использования симплексного метода ЗЛП должна
быть приведена к каноническому виду. Для реализации симплексного метода необходимо
освоить 3 основных элемента:
способ определения какого – либо первоначального допустимого решения
правило перехода к лучшему решению
критерий проверки оптимальности найденного решения.
Пусть имеется задача ЛП:
Слайд 15Канонический вид задачи ЛП:
F(x1 , x2 ,.., xn)=c1 x1+ c2
x2+..+ cn xn max
Слайд 16Определения:
Ненулевое допустимое решение
называется опорным, если векторы Aj, соответствующие отличным
от 0 координатам вектора x, линейно независимы.
Ненулевое опорное решение называют
невырожденным, если оно имеет ровно m положительных координат.
Если число положительных координат меньше m, то оно называется вырожденным.
Упорядоченный набор из m линейно независимых координат векторов Aj , соответствующих положительным координатам опорного решения называют базисом.
Слайд 17Критерий оптимальности
Вектор
тогда и только тогда является опорным решением задачи, когда
точка X является вершиной допустимого множества.
Используя разложение Aj по базису
сформулировали следующий критерий:
Если для данного базиса Aj1, Aj2, …. Ajm все оценки j ,
(j=ci aij – cj ) неотрицательны, то опорное решение Xоп
является оптимальной точкой задачи.
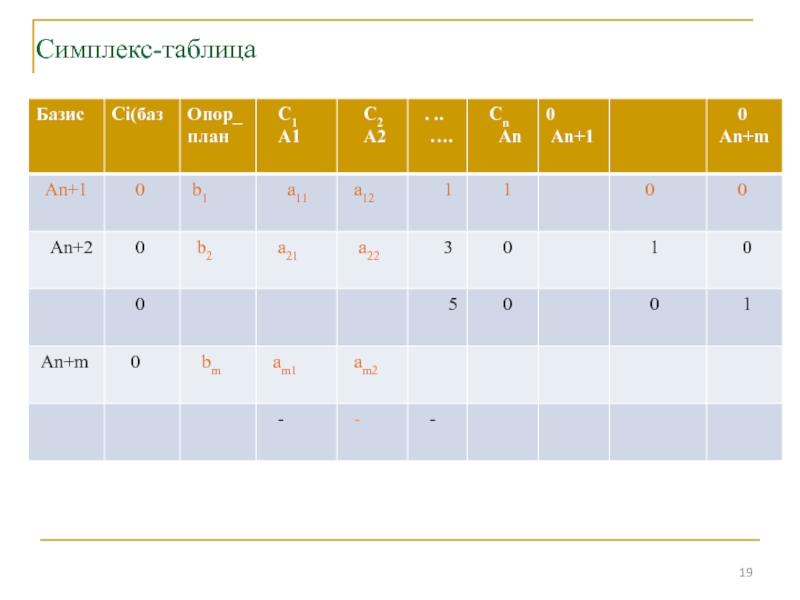
Слайд 18Алгоритм симплекс-метода:
Пусть задача ЛП имеет непустое допустимое множество с вершинами.
Тогда
1) Тем или иным способом находим какую-нибудь вершину допустимого мн-ва
и определяем не является ли она оптимальной. Если оптимальна, то задача решена. Если нет, то
2) Используя определённые правила проверяем нельзя ли утверждать, что задача не имеет оптимального решения. Если можно утверждать, то задача не имеет решения. Если нельзя, то
3) По определённому правилу ищем новую лучшую вершину и переходим к пункту 1.
Слайд 20Алгоритм симплекс-метода:
Вычисляют (j=ci aij – cj ). Выбирают из отрицательных
j
наименьшее, например к. к–й столбец - разрешающий.
Наименьшее положительное симплексное
отношение определяет разрешающую строку: min bi / aik )= bs / ask . Строка s – разрешающая.
На пересечении разрешающего столбца и разрешающей строки – разрешающий элемент, который показывает какой вектор выводится из базиса, какой вектор вводится в базис.
Слайд 21Алгоритм симплекс-метода:
В новой симплекс-таблице элементы разрешающей строки вычисляют делением на
разрешающий элемент, остальные элементы – по правилу прямоугольника:
Из произведения элементов
главной диагонали (разрешающий элемент соединяют с искомым) вычитают произведение элементов побочной диагонали и делят на разрешающий элемент.
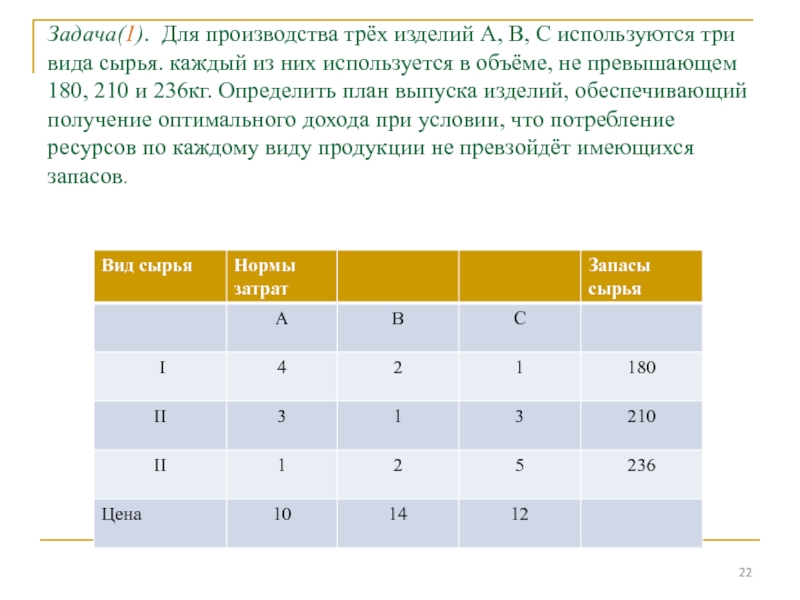
Слайд 22Задача(1). Для производства трёх изделий А, В, С используются три
вида сырья. каждый из них используется в объёме, не превышающем
180, 210 и 236кг. Определить план выпуска изделий, обеспечивающий получение оптимального дохода при условии, что потребление ресурсов по каждому виду продукции не превзойдёт имеющихся запасов.
Слайд 23Экономико-математическая модель задачи:
F= 10x1+14x2+12x3→max
При ограничениях:
4х1+2х2+х3≤180
3х1+х2+3х3≤210
х1+2х2+5х3≤236
условие неотрицательности переменных
x1≥0, x2≥0, х3≥0.
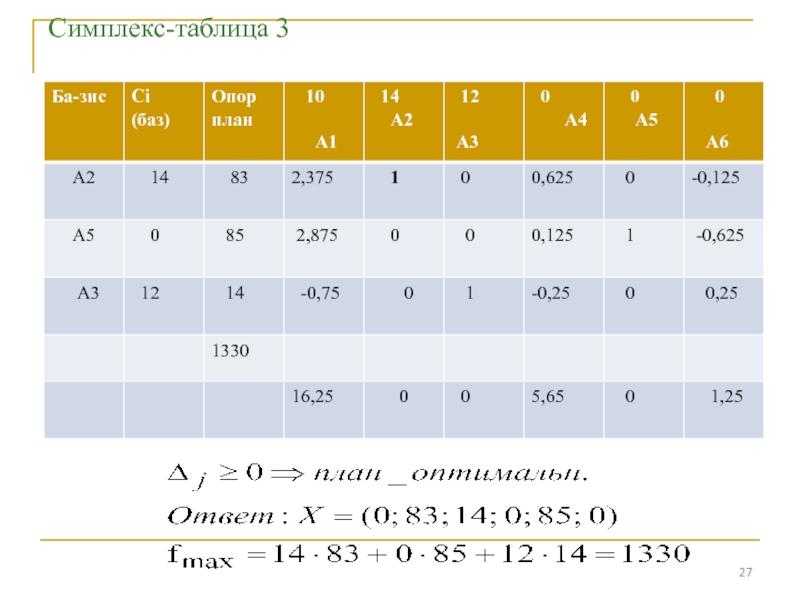
Слайд 24Каноническая форма задачи:
F= 10x1+14x2+12x3 +0x4 + 0x5 + 0x6 →max
При ограничениях:
4х1+2х2+х3+ x4 = 180
3х1+х2+3х3 + x5 = 210
х1+2х2+5х3 + x6 = 236
условие неотрицательности переменных
x1≥0, x2≥0, х3≥0, x4≥0, x5≥0, х6≥0.
Слайд 28Метод искусственного базиса:
F= 0,4x1+0,3x2 → min
При ограничениях:
х1+х2≥50
х1≤35
х2 ≥ 15
x1≥0, x2≥0.
Канонический вид задачи:
F1= -0,4x1-0,3x2 → max
При ограничениях:
х1+х2 – х3 =50
х1 + х4 = 35
х2 – х5 = 15
x1≥0,…, x5≥0.
Слайд 29Вспомогательная задача:
F2= -x6 - x7 → max
При ограничениях:
х1+х2 – х3 + х6 = 50
х1 + х4 = 35
х2 – х5 + х7 = 15
x1≥0,…, x7 ≥0.
Решаем симплексным методом до тех пор, пока векторы для искусственных переменных х6 и х7 не
выведутся из базиса. Коэффициенты Cj записываем из канонического вида задачи и решаем симплексным методом.
Если какой-либо вектор для искусственной переменной не выводится из базиса, то задача не имеет решения.