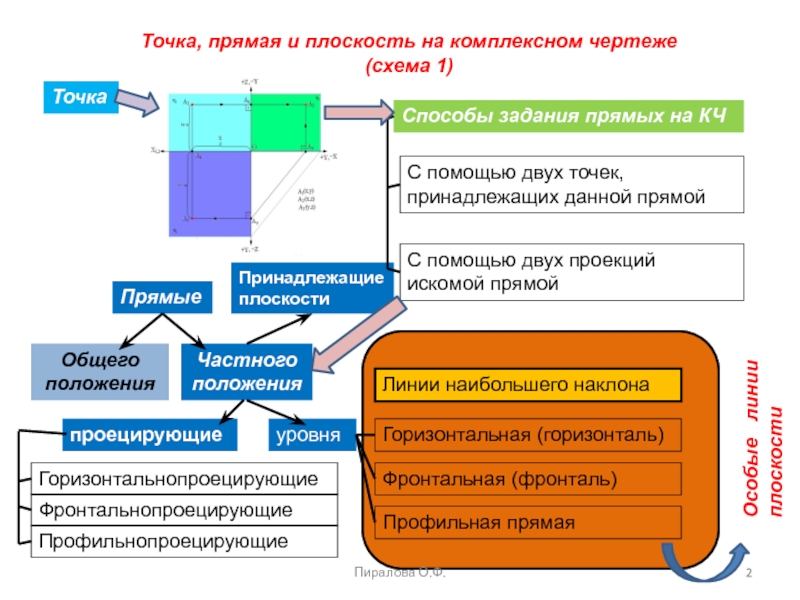
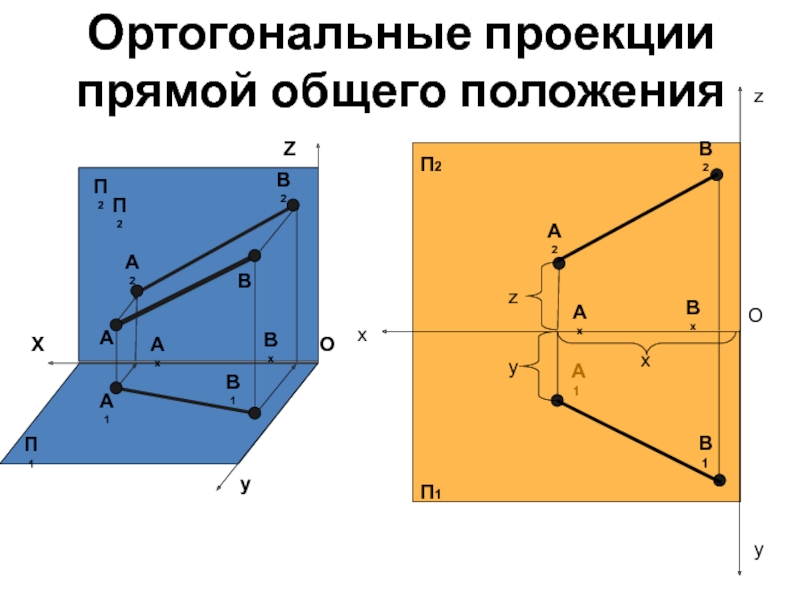
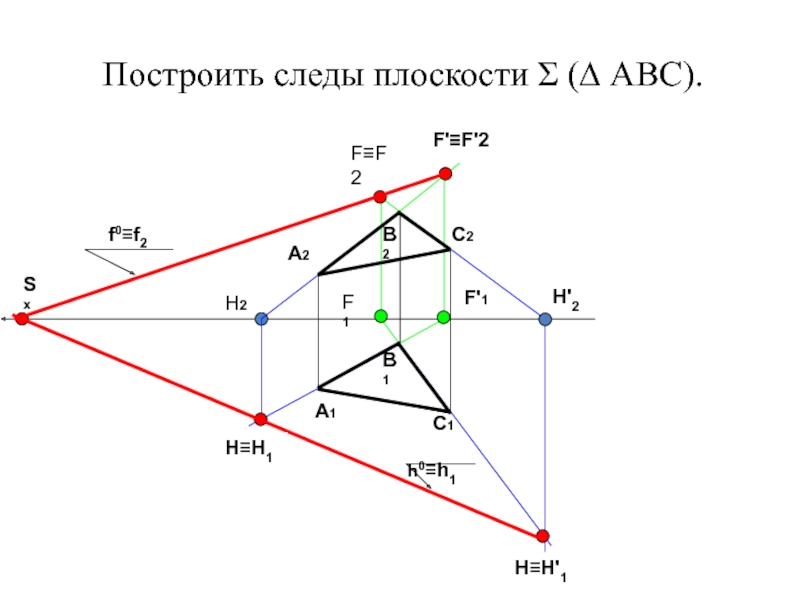
положения
Частного положения
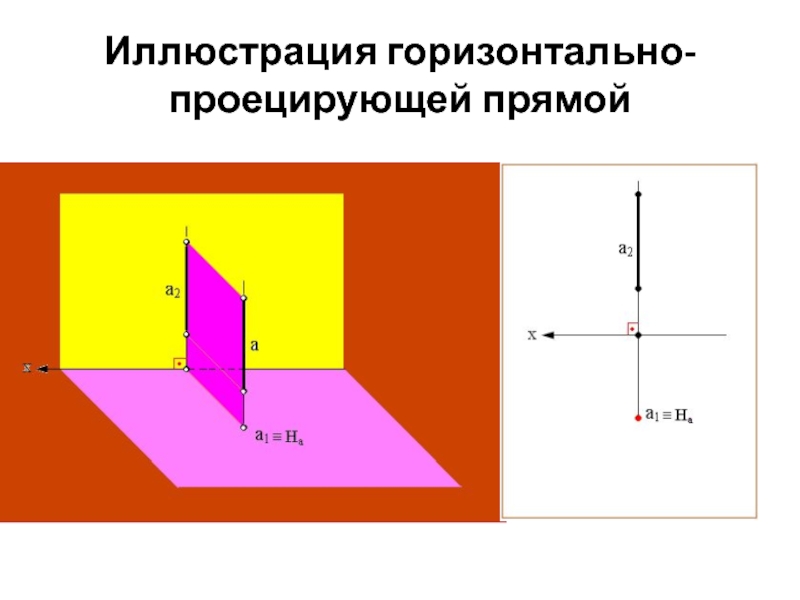
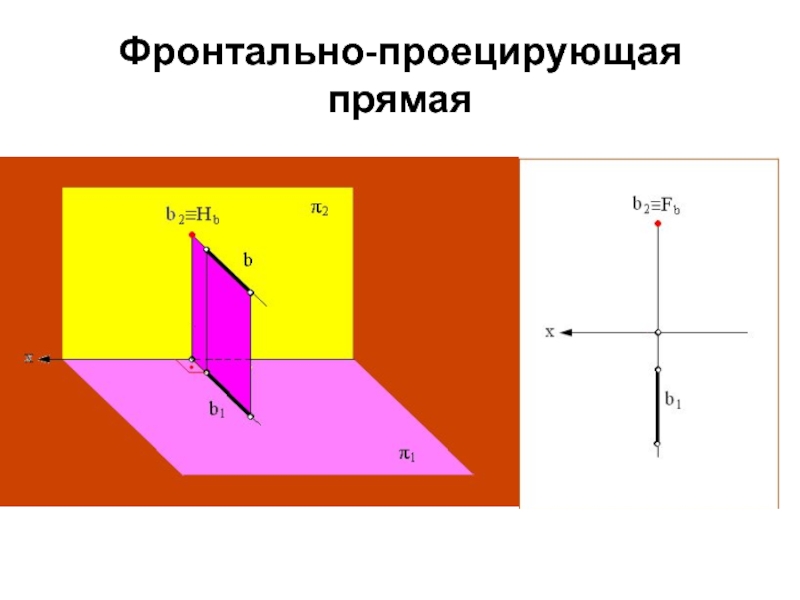
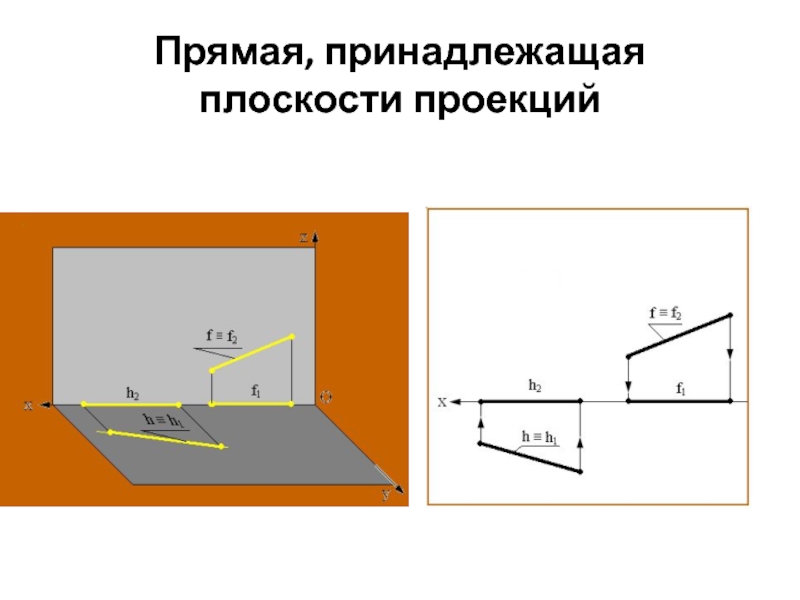
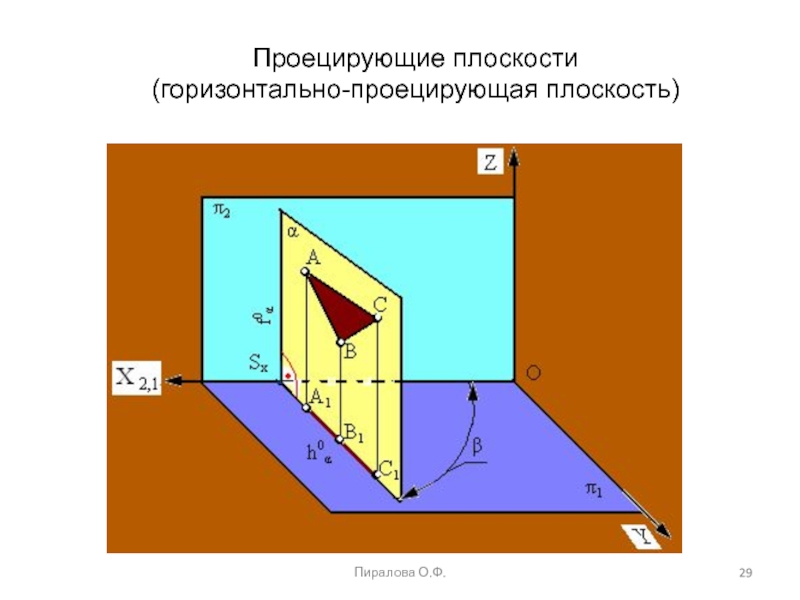
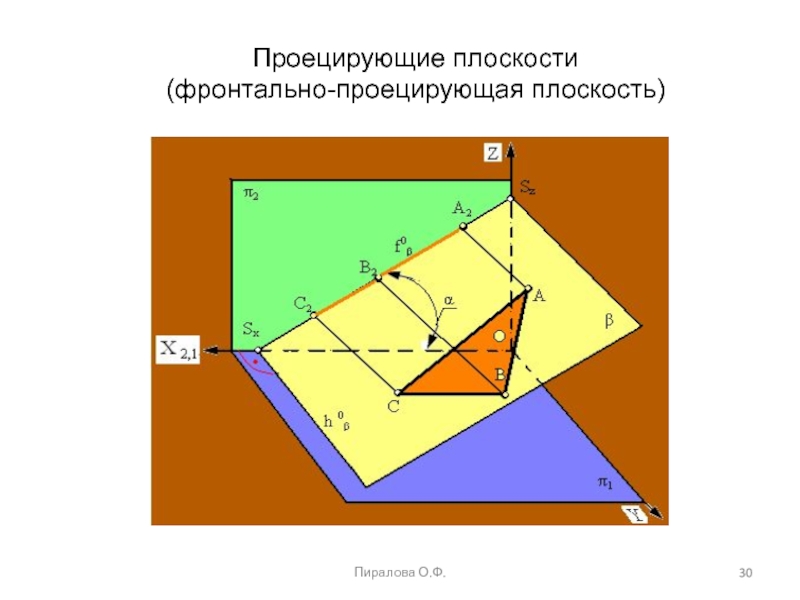
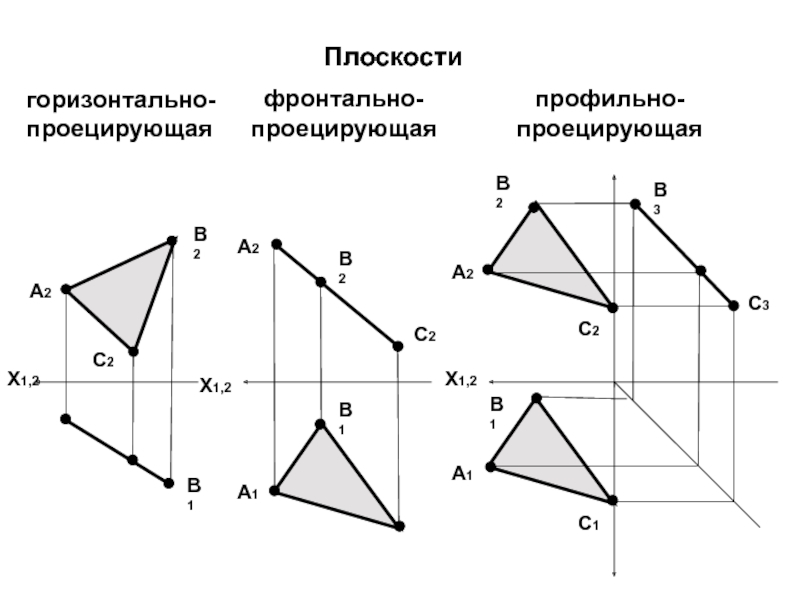
проецирующие
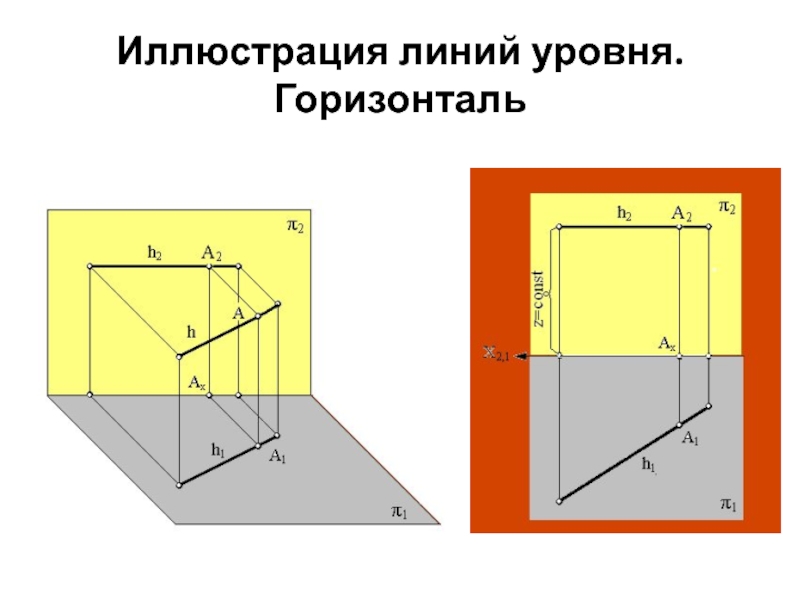
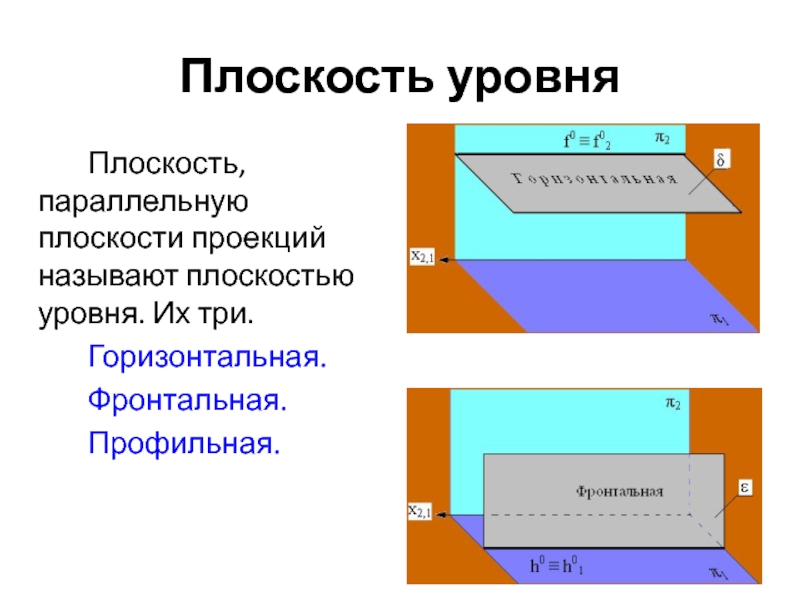
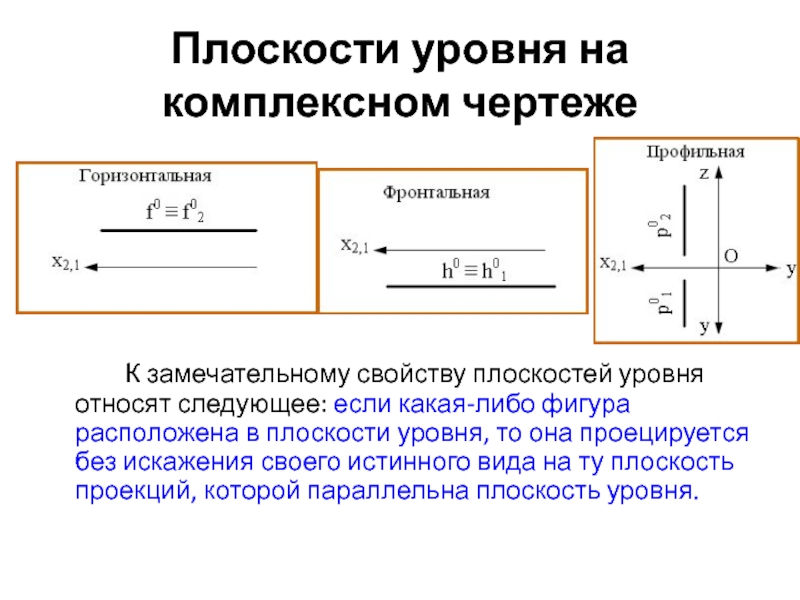
уровня
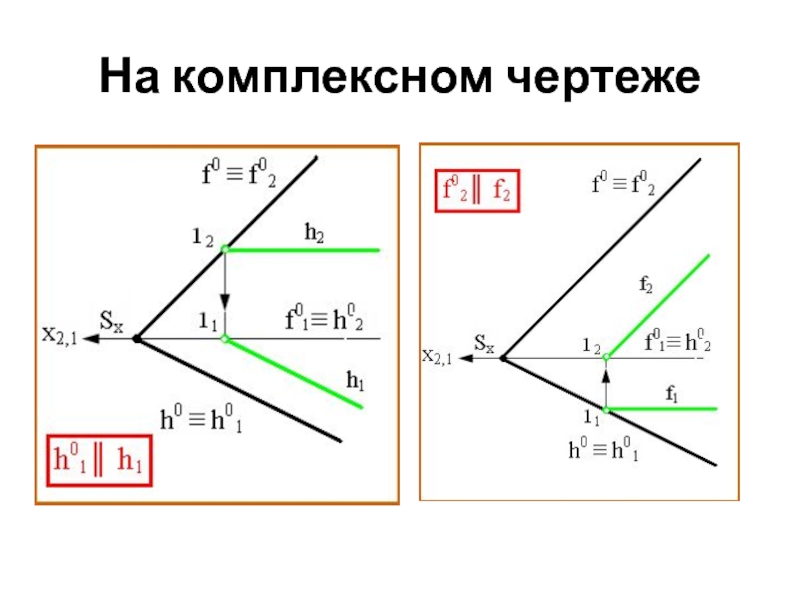
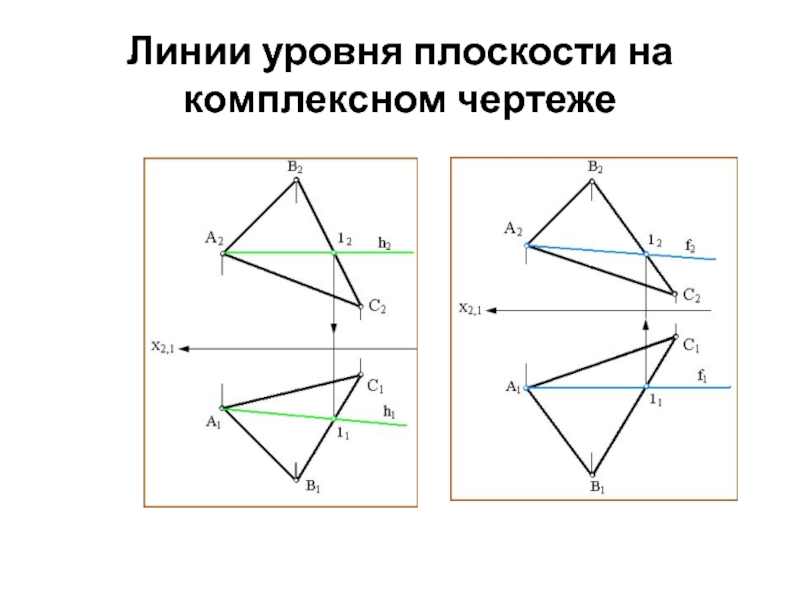
Горизонтальная (горизонталь)
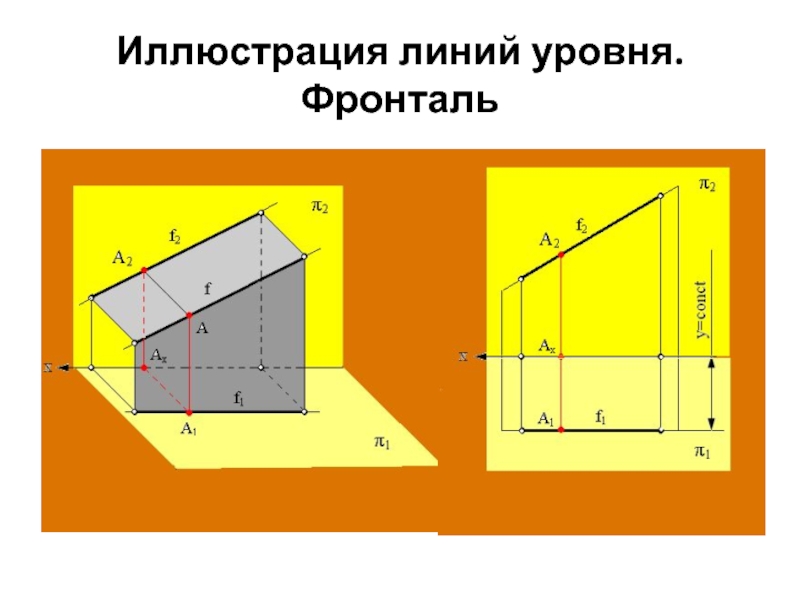
Фронтальная (фронталь)
Профильная прямая
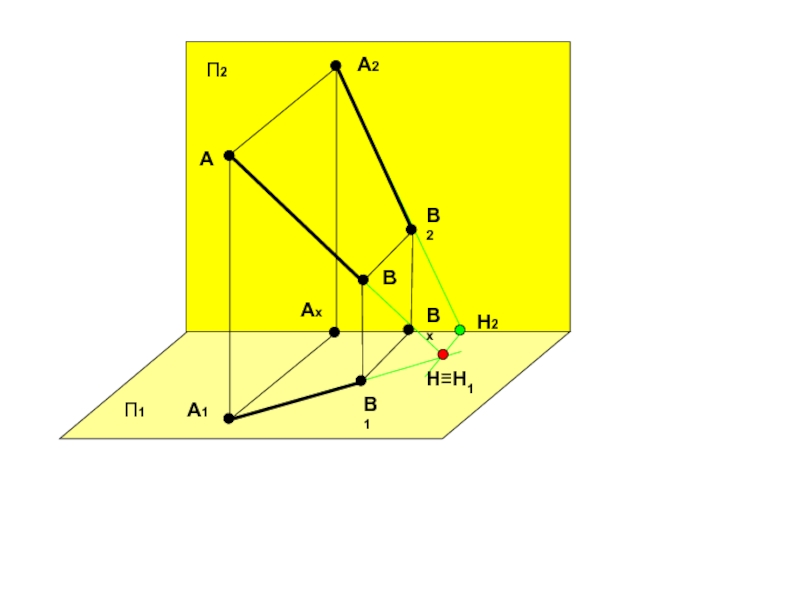
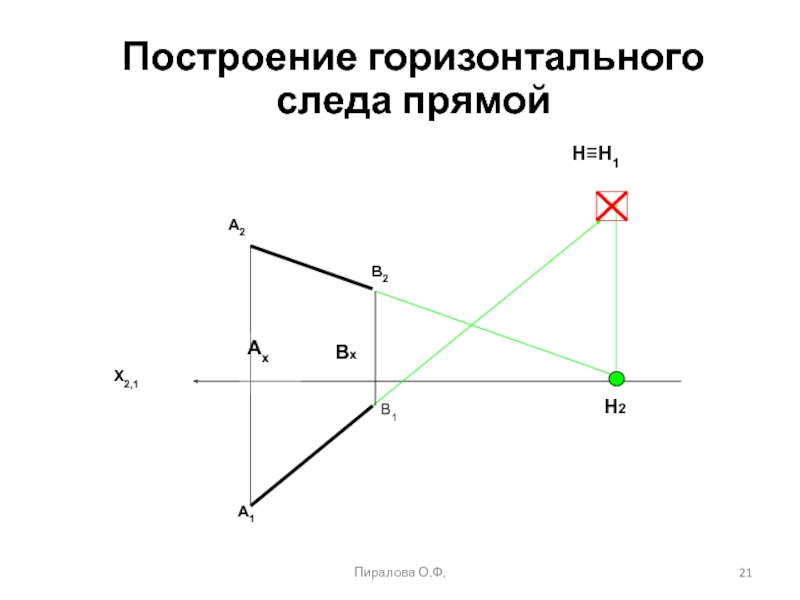
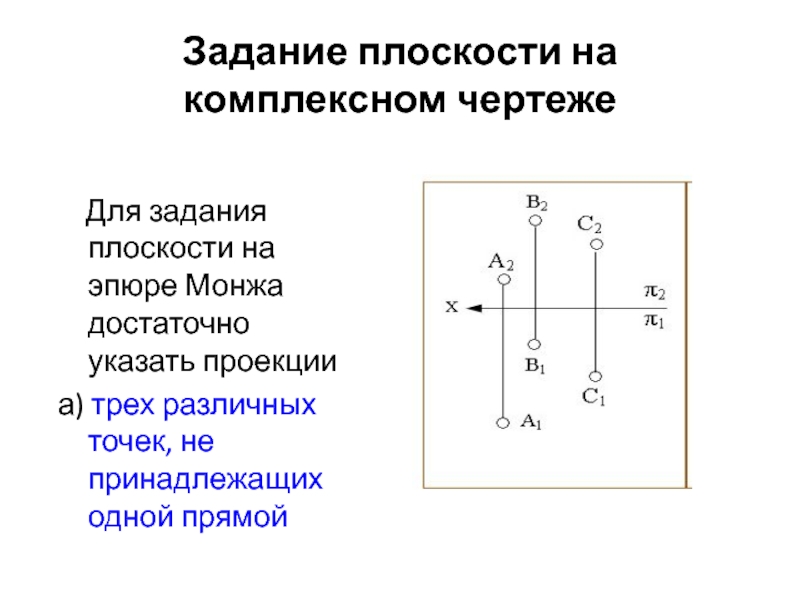
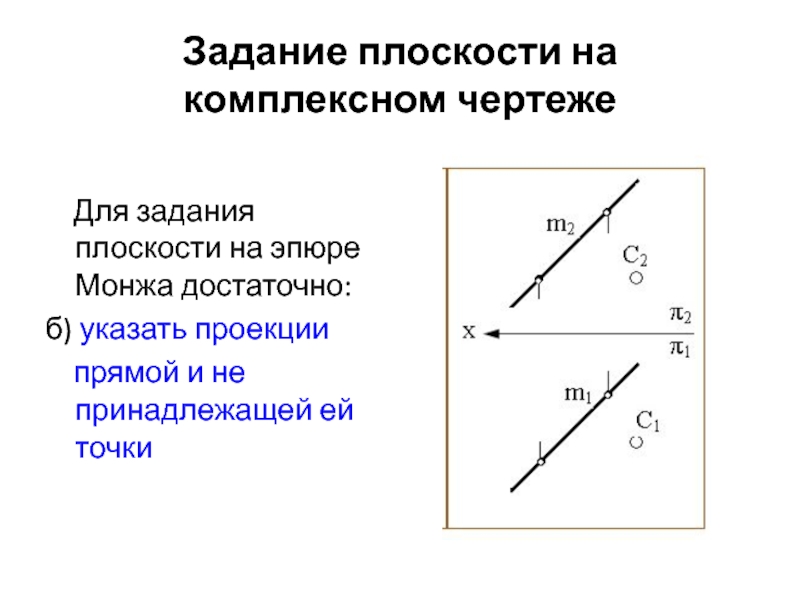
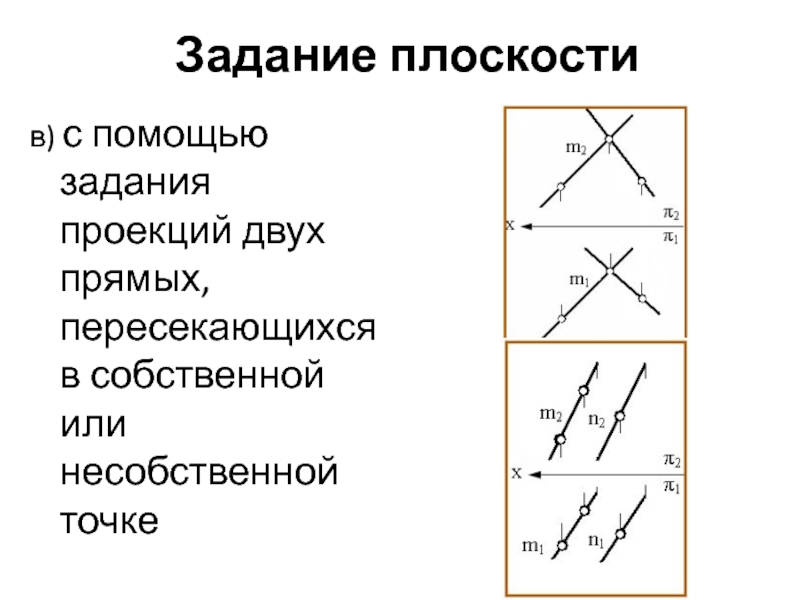
Способы задания прямых на КЧ
С помощью
двух точек, принадлежащих данной прямойС помощью двух проекций искомой прямой
Пиралова О.Ф.
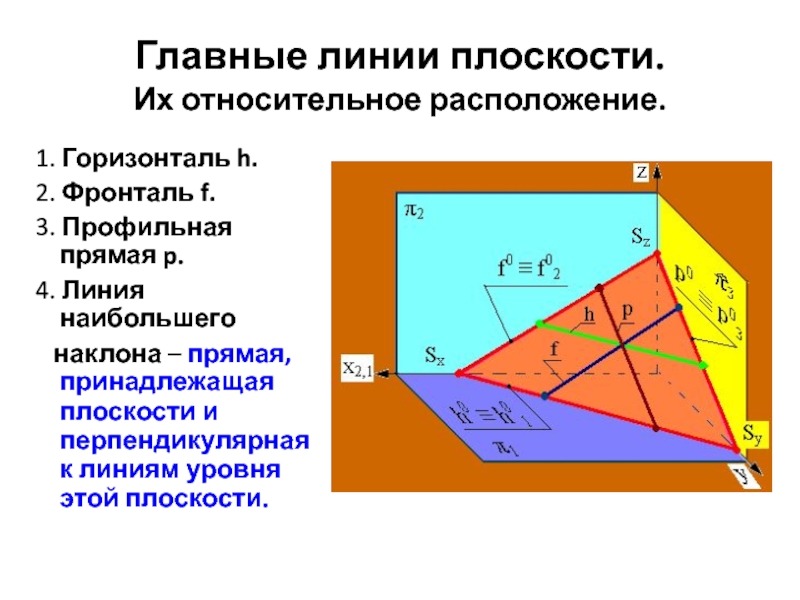
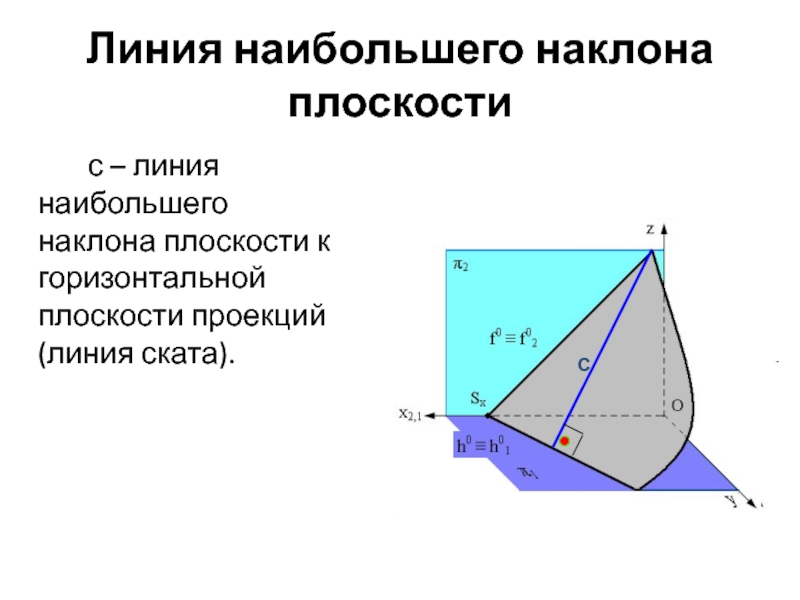
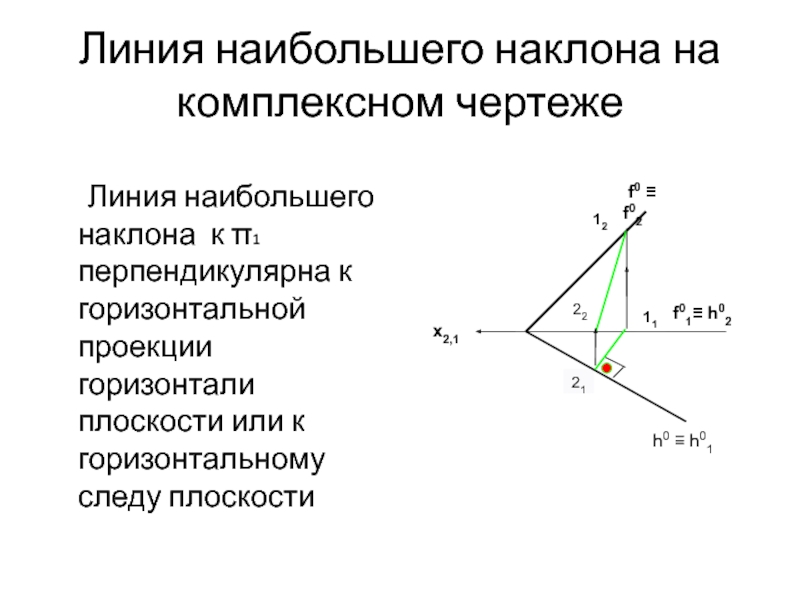
Линии наибольшего наклона
Особые линии плоскости