Слайд 1Лекция 2
Биореология
Гидродинамика. Биофизика мышечных сокращений.
Слайд 2Реология
– учение о деформации и текучести вещества.
(rheos – течение, поток)
Идеальная
жидкость – жидкость, плотность которой не зависит от давления и
постоянна в любой пространственной области, а вязкость (внутреннее трение) отсутствует.
При движении идеальной жидкости не происходит превращения механической энергии в тепловую, то есть механическая энергия жидкости сохраняется.
Слайд 3
Закон Бернулли является следствием закона
сохранения энергии для стационарного потока идеальной несжимаемой жидкости:
ρ— плотность жидкости,
- скорость потока,
h - высота,
p – давление,
g - ускорение свободного падения
Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости (динамического давления) статическое давление падает.
Даниил БЕРНУЛЛИ
(1700–1782)
Для горизонтальной трубы h = 0 и уравнение Бернулли принимает вид:
Слайд 4
Внутреннее трение (вязкость жидкости). Уравнение
Ньютона
Вязкость (внутреннее трение) – это свойство текучих тел
(жидкостей
и газов)
оказывать сопротивление перемещению одной их части относительно другой.
Основной закон вязкого течения был установлен Ньютоном (1713)
Течение жидкости по трубе
Слайд 5-уравнение Ньютона
Формулировка: сила внутреннего трения F между слоями движущейся жидкости
прямо пропорциональна скорости сдвига , площади поверхности
соприкасающихся слоев S. Коэффициентом пропорциональности является коэффициент вязкости η.
Река
v+dv
v
dx
Между слоями существует градиент скорости = скорость сдвига:
=
Слайд 6-напряжение сдвига
В реологических характеристиках
уравнение Ньютона имеет вид:
Напряжение сдвига прямо
пропорционально скорости сдвига.
η – коэффициент динамической вязкости
[Па]
СИ:
[Па•с] = паскаль•секунда
СГС: [П] = пуаз 1 Па•с = 10 П 1мПа•с = 1сП
Слайд 7Вязкость зависит от
температуры
Природы жидкости
Формы молекул
Кинематическая вязкость
[Ст] = стокс
Текучесть-
величина обратная
вязкости
t
η
Для жидкостей
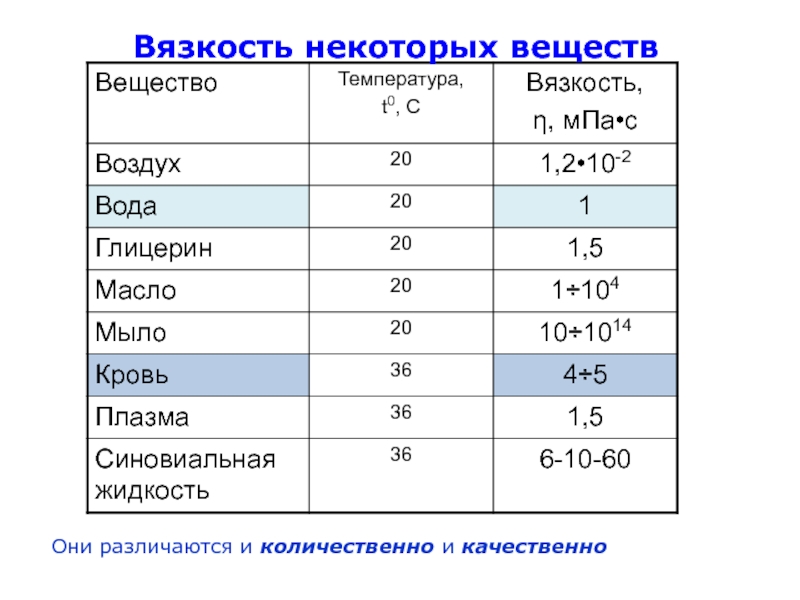
Слайд 8Вязкость некоторых веществ
Они различаются и количественно и качественно
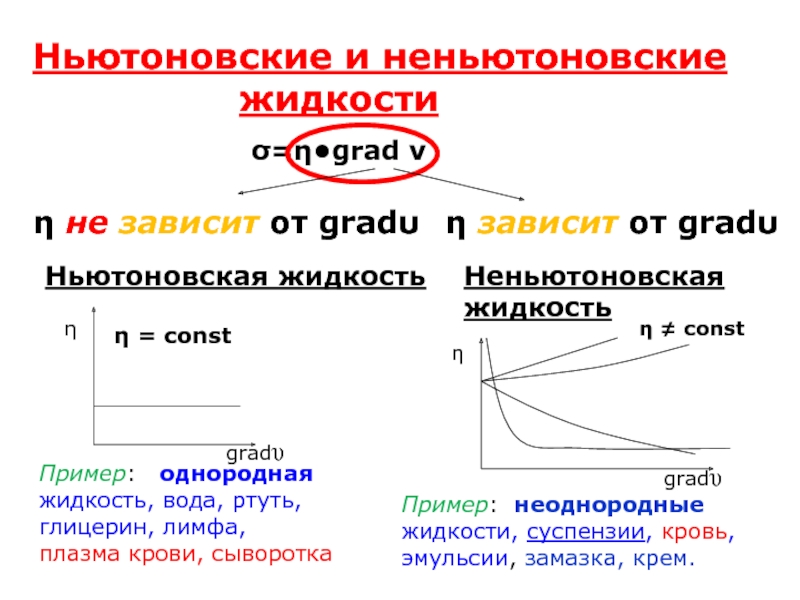
Слайд 9
Ньютоновские и неньютоновские
жидкости
Ньютоновская жидкость
σ=η•grad ν
Неньютоновская жидкость
η = const
gradυ
η не зависит
от gradυ
η
η зависит от gradυ
Пример: однородная жидкость, вода, ртуть, глицерин, лимфа,
плазма крови, сыворотка
η ≠ const
gradυ
η
Пример: неоднородные жидкости, суспензии, кровь, эмульсии, замазка, крем.
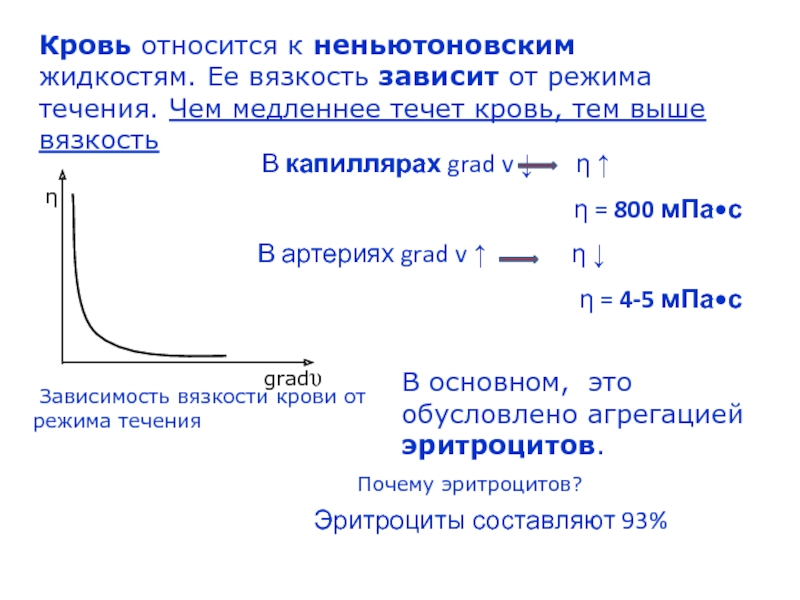
Слайд 10Кровь относится к неньютоновским жидкостям. Ее вязкость зависит от режима
течения. Чем медленнее течет кровь, тем выше вязкость
η
gradυ
Зависимость вязкости
крови от режима течения
В основном, это обусловлено агрегацией эритроцитов.
Почему эритроцитов?
Эритроциты составляют 93%
В капиллярах grad v ↓ η ↑
η = 800 мПа•с
В артериях grad v ↑ η ↓
η = 4-5 мПа•с
Слайд 11При низких скоростях сдвига (в неподвижной крови) эритроциты образуют «монетные
столбики» - клеточные агрегаты.
При высоких скоростях сдвига вязкость крови
определяется
1) Концентрацией эритроцитов
2 ) Их физическими свойствами.
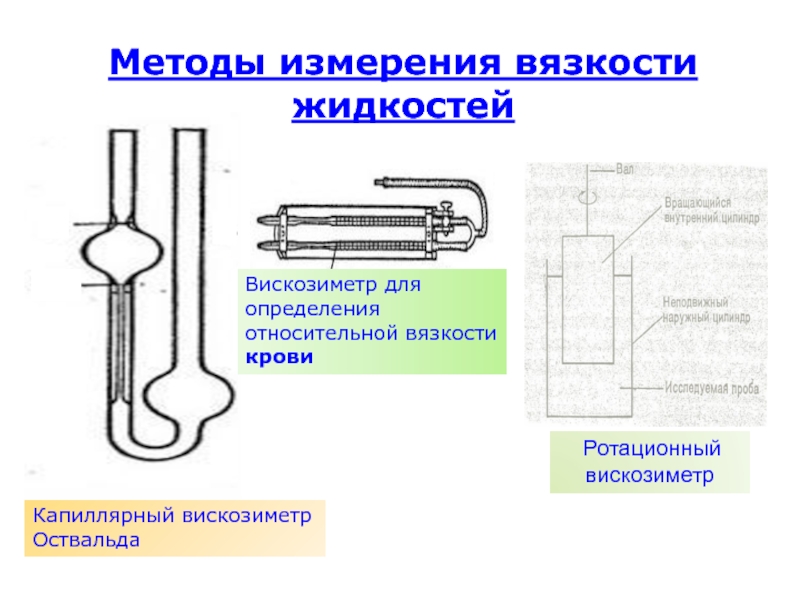
Слайд 12Методы измерения вязкости жидкостей
Капиллярный вискозиметр Оствальда
Ротационный вискозиметр
Вискозиметр для
определения относительной вязкости крови
Слайд 13
Вискозиметр VT550 - высокоточная модель с широким
диапазоном измерения, ручной или автоматический режим
под управлением компьютера.
Ротационный вискозиметр
Rheotest RV2.1
Наиболее простая модель ротационного вискозиметра,
Устройство работает без применения персонального компьютера, имеет аналоговый дисплей и выход на самописец.
Экспресс-анализатор-вискозиметр ротационный
Слайд 14Ламинарное и турбулентное течение
Ламинарное течение- это слоистое течение.
слои жидкости движутся
параллельно, не смешиваясь между собой
Турбулентное течение – это вихревое
течение- жидкости сопровождающееся перемешиванием слоев, обусловленным образованием вихрей. Скорость частиц непрерывно меняется.
Слайд 15
Характер течения жидкости определяется числом Рейнольдса
РЕЙНОЛЬДС, ОСБОРН
(1842–1912),
английский инженер и физик.
В 1883 Рейнольдс установил, что ламинарное течение
переходит в турбулентное, когда введенное им число Рейнольдса превышает критическое значение.
Величина безразмерная
Если Re < Reкр => Ламинарное течение
Если Re > Reкр = > Турбулентное течение
Слайд 16 Ламинарное течение вязкой жидкости в цилиндрических трубах
Наибольшая скорость у
частиц вдоль оси трубы. Профиль скорости параболический.
Примерное распределение скорости частиц
жидкости в продольном сечении глицерина
Слайд 17Пуазейль
Формула Пуазейля
Пуазейль Жан Мари французский
врач + физик+ физиолог
(1799-1869)
Преподавал медицинскую физику
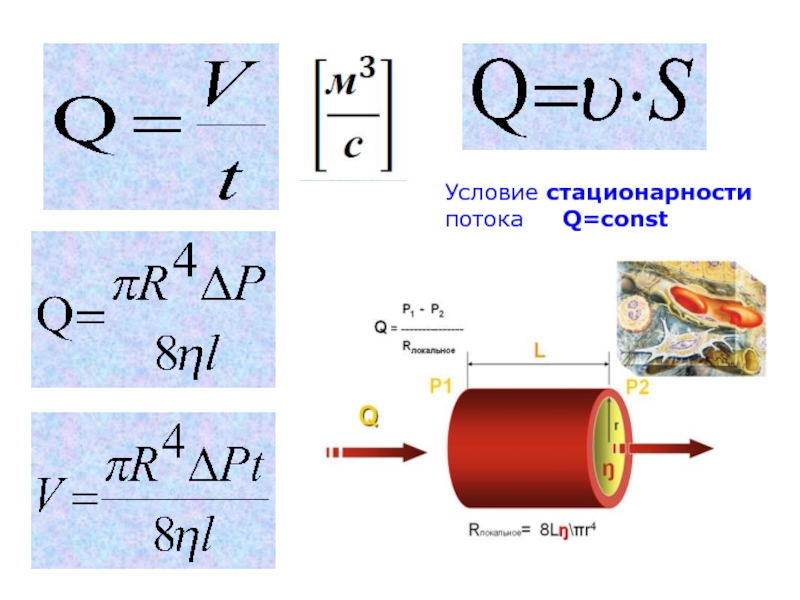
Формулировка: Объём жидкости Q,
протекающей по горизонтальной трубе небольшого сечения за единицу времени, прямо пропорционален радиусу трубы R в четвёртой степени, разности давлений ∆P на концах трубы, обратно пропорционален коэффициенту вязкости η и длине трубы ι. Коэффициентом пропорциональности является π/8 (получен эмпирически).
Слайд 18Условие стационарности
потока Q=const
Слайд 19Гидравлическое сопротивление
=>
Основное уравнение
гемодинамики
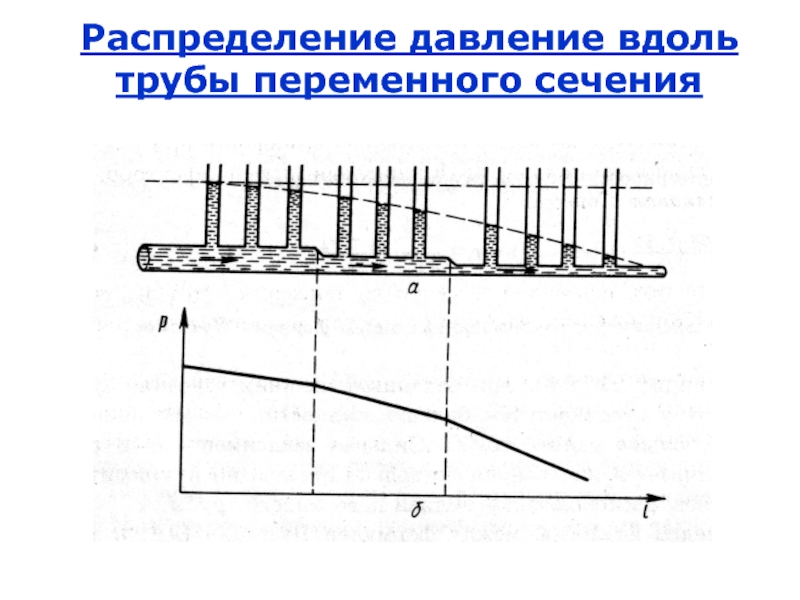
Слайд 20Распределение давление вдоль трубы переменного сечения
Слайд 21
ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫЕ ТРУБЫ РАЗЛИЧНОГО СЕЧЕНИЯ
Сужение
трубы
Скорость потока возрастает
Сопротивление увеличивается
↑
↓S٠υ↑=const
↑∆P=Q٠x↑
Перепад давлений увеличивается
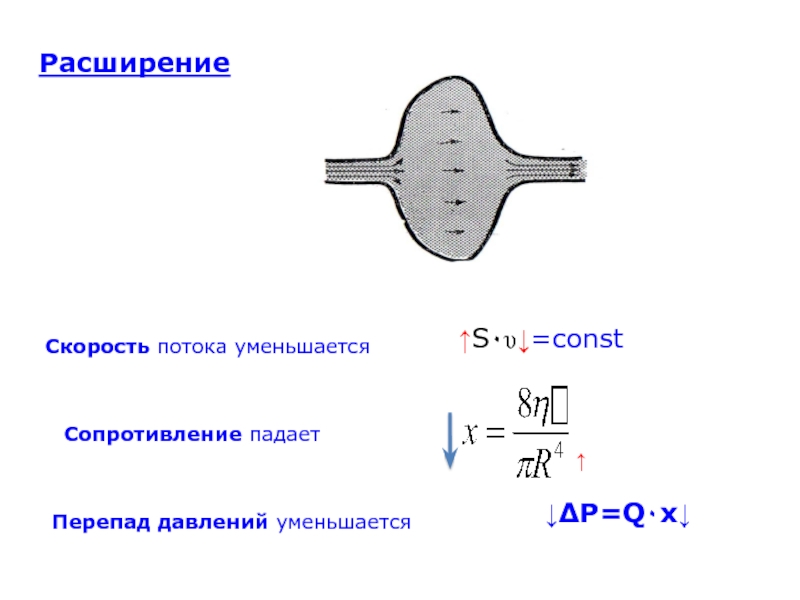
Слайд 22Расширение
Скорость потока уменьшается
Сопротивление падает
Перепад давлений уменьшается
↑S٠υ↓=const
↑
↓∆P=Q٠x↓
Слайд 23Особенности движения пульсирующего потока жидкости по трубам с эластичными стенками.
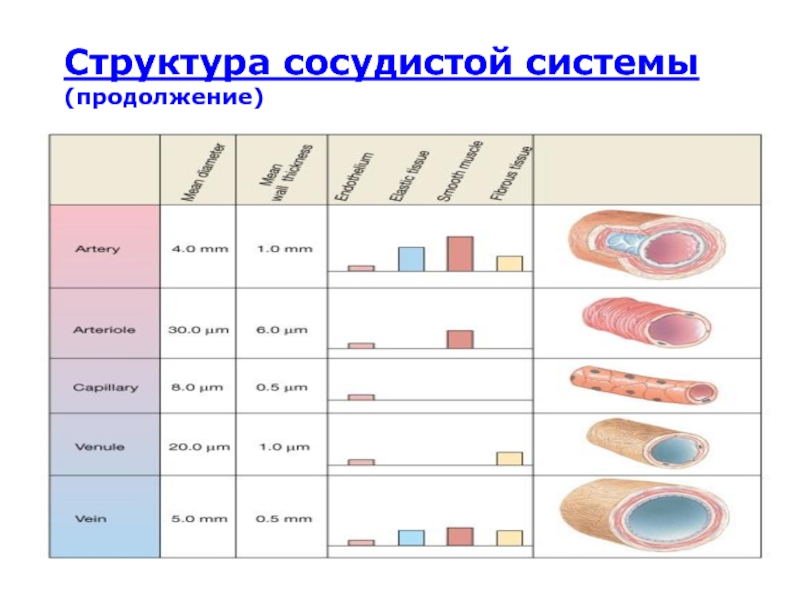
Слайд 24Структура сосудистой системы (продолжение)
Слайд 25Пульсовая волна - это волна деформации стенок артерии.
Пульсовая волна –
это распространяющаяся по аорте и артериям волна повышенного давления, вызванная
выбросом крови из левого желудочка в аорту в период систолы.
Причина: упругость аортальной стенки
Слайд 26СРПВ –количественный показатель упругих свойств артерии.
Формула Моенса- Кортевега
Скорость распространения
пульсовой волны v
Е –модуль Юнга
h- толщина стенки
d –диаметр сосуда
ρ –
плотность крови
В норме 5-10 м/с.
Что происходит с СРПВ с возрастом?
Она увеличивается
Слайд 27Распределение скоростей и давлений крови в различных отделах ССС
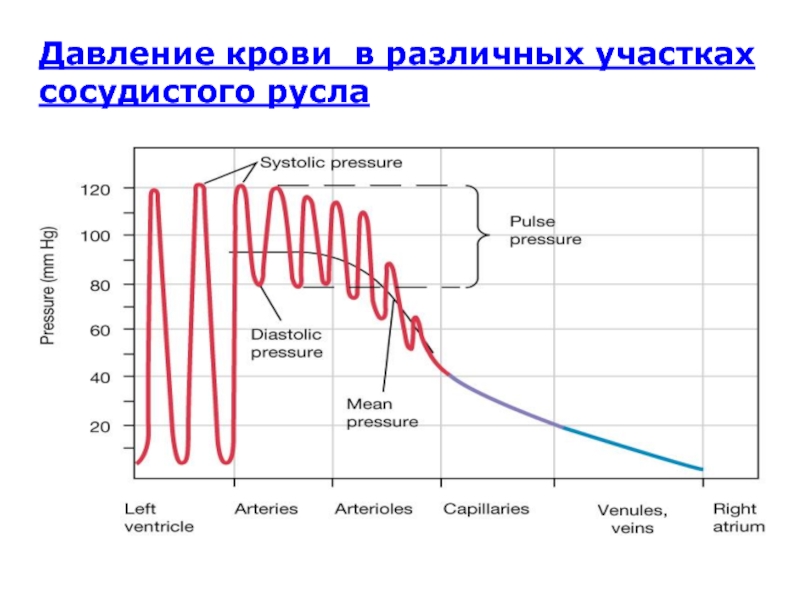
Давление крови
в артериях колеблется от максимального во время сокращения сердца (систолы)
до минимального во время расслабления (диастолы).
Поэтому артериальное давление (АД) определяют как максимальное/минимальное значения (систолическое/диастолическое).
АД в норме для здоровых взрослых людей
120/80 мм рт.ст.
16/11 кПа
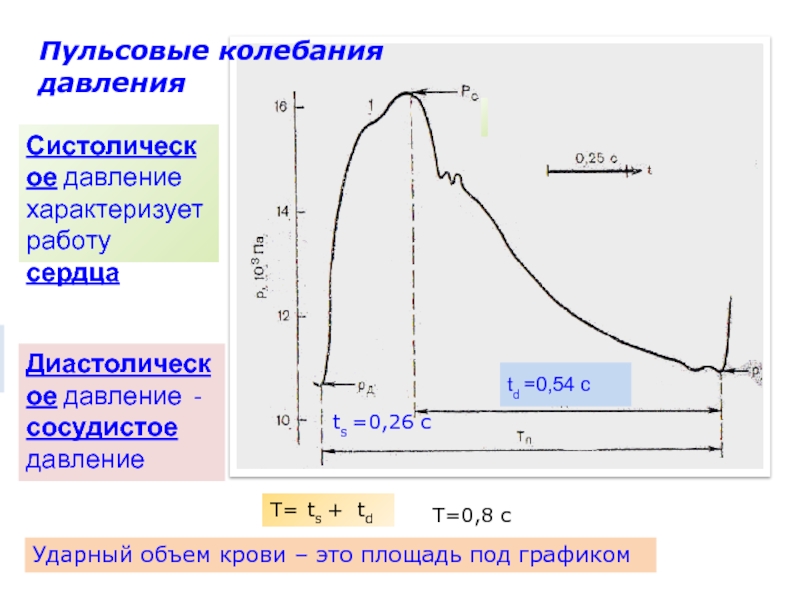
Слайд 28Систолическое давление характеризует работу сердца
Диастолическое давление -сосудистое давление
ts =0,26 с
td
=0,54 с
T=
ts +
td
T=0,8 с
Ударный объем крови – это площадь под
графиком
Пульсовые колебания давления
Слайд 29Давление крови в различных участках сосудистого русла
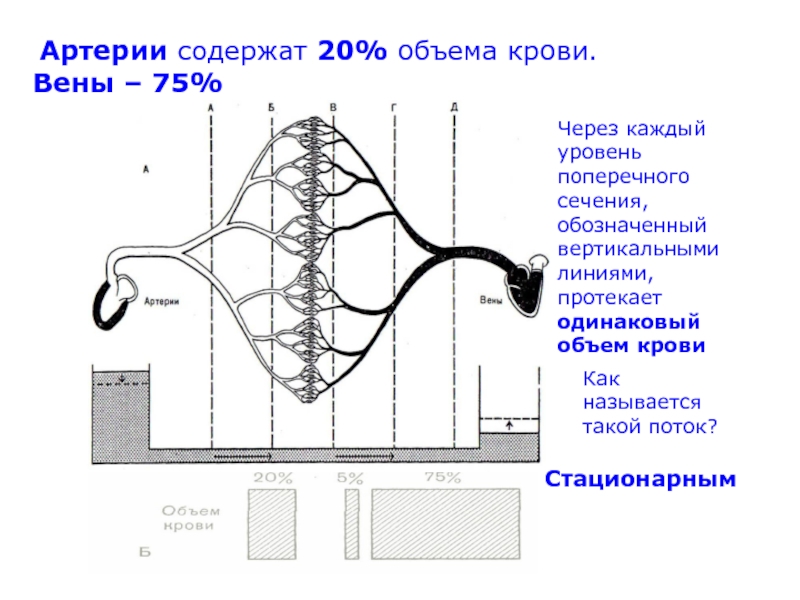
Слайд 30 Артерии содержат 20% объема крови.
Вены – 75%
Через каждый
уровень поперечного сечения, обозначенный вертикальными линиями, протекает одинаковый объем крови
Как
называется такой поток?
Стационарным
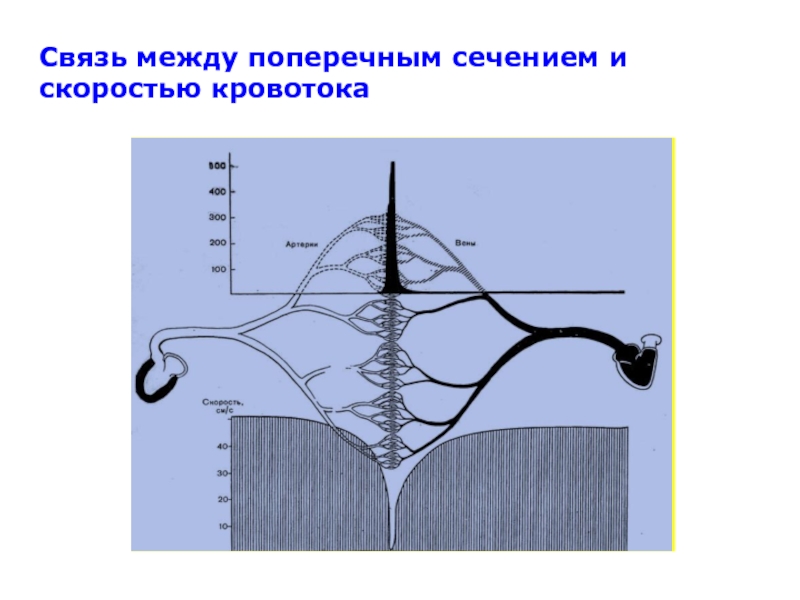
Слайд 31Скорость течения крови также значительно различается в разных отделах кровеносной
системы. Она определяется уравнением неразрывности струи.
НАПРИМЕР:
Площадь поперечного сечения аорты в
600 раз меньше, чем капилляров. Поэтому в капиллярах скорость кровотока низкая.
Vаорт. =0,5 м/с
Vкапил.= 0,5 мм/с
Слайд 32Связь между поперечным сечением и скоростью кровотока
Слайд 33Физические основы клинического метода измерения давления крови. Прибор для измерения
давления крови
Основан на измерении внешнего давления, необходимого, чтобы пережать артерию.
СФИГМОМАНОМЕТР=
=
Манжета +груша + манометр
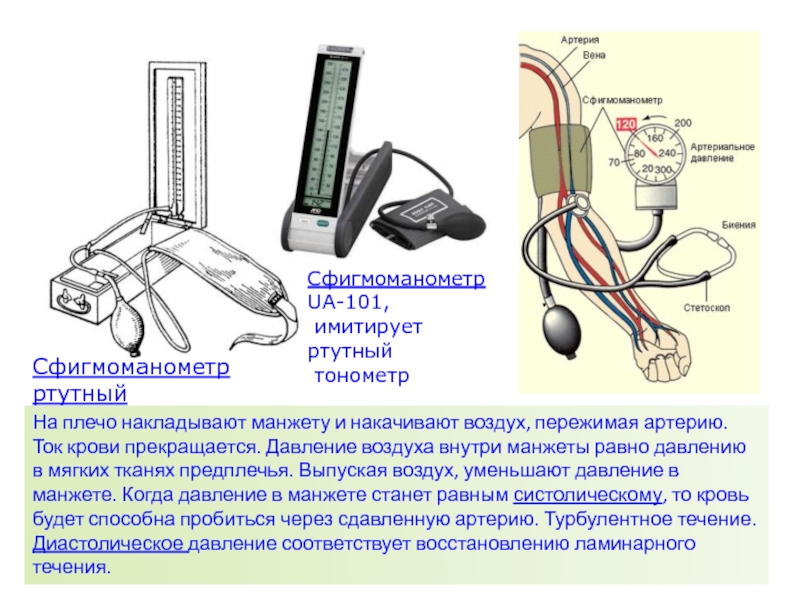
Слайд 34Сфигмоманометр
ртутный
Сфигмоманометр
UA-101,
имитирует ртутный
тонометр
На плечо накладывают манжету и
накачивают воздух, пережимая артерию. Ток крови прекращается. Давление воздуха внутри
манжеты равно давлению в мягких тканях предплечья. Выпуская воздух, уменьшают давление в манжете. Когда давление в манжете станет равным систолическому, то кровь будет способна пробиться через сдавленную артерию. Турбулентное течение. Диастолическое давление соответствует восстановлению ламинарного течения.
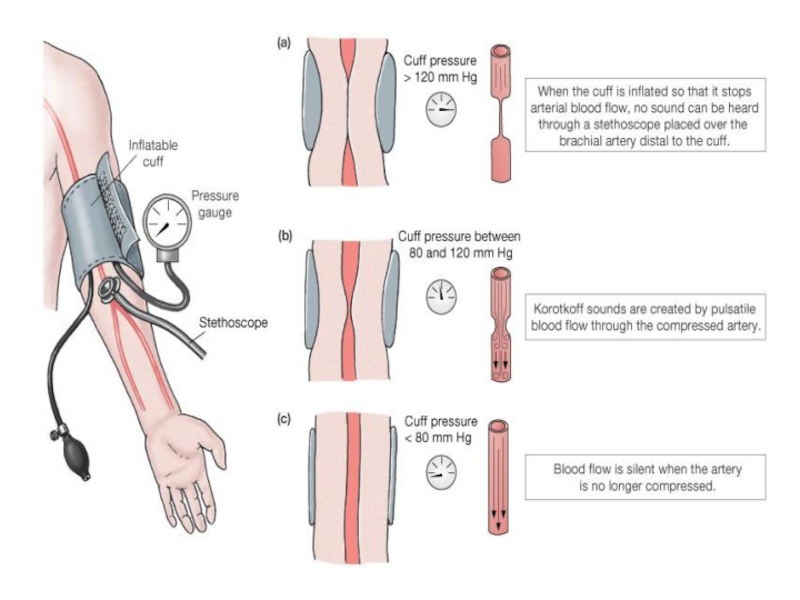
Слайд 35Метод Короткова
по измерению АД
105-ЛЕТИЕ НАУЧНОГО ОТКРЫТИЯ ХИРУРГА ВОЕННО-МЕДИЦИНСКОЙ АКАДЕМИИ
Н.С.КОРОТКОВА, СДЕЛАВШЕГО ЭПОХУ В РАЗВИТИИ МИРОВОЙ МЕДИЦИНЫ
В созвездии имен великих
медиков, заслуживших благодарность всего человечества за свои открытия в медицине, нашло свое место имя русского врача Николая Сергеевича Короткова.
8 ноября 1905 года Н.С. Коротков (ему был 31 год) в своем докладе на «Научном Совещании Клинического военного госпиталя Военно-медицинской академии» сообщил об открытом им звуковом методе бескровного определения максимального и минимального артериального давления (АД) у человека
Слайд 36
Измерение артериального давления методом Короткова (аускультативный метод)
Основан на возникновении
турбулентного течения, когда давление в манжете станет равным систолическому давлению.
Слайд 38Мышечные сокращения
Мышца – это биологическая система, способная преобразовывать химическую энергию
(АТФ)
в тепловую и механическую.
КПД мышцы = 45-80%.
Если
бы мышца работала как тепловая машина, то ее температура была 2150 С !
Если учесть, что процессы синтеза АТФ имеют КПД ≈ 50%, то полная эффективность превращения энергии питательных веществ в механическую энергию ≈ 20 %.
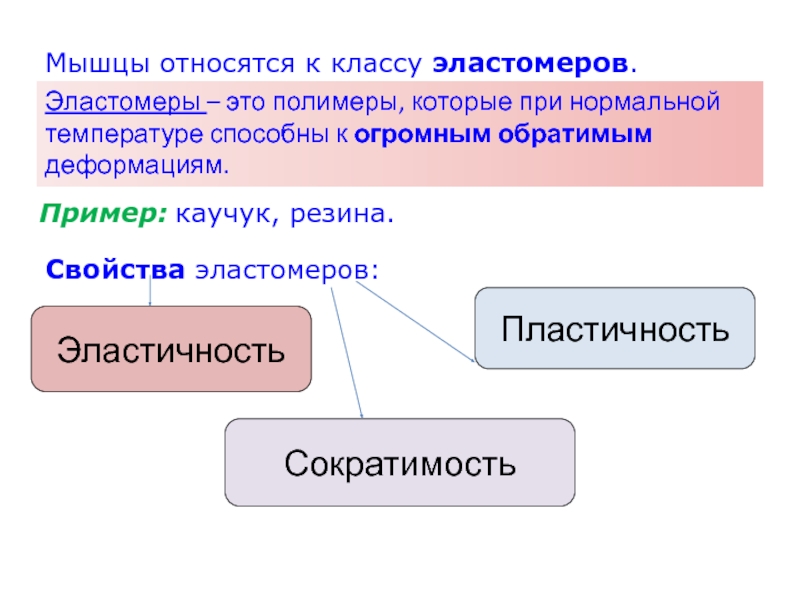
Слайд 39Мышцы относятся к классу эластомеров.
Эластомеры – это полимеры, которые при
нормальной температуре способны к огромным обратимым деформациям.
Пример: каучук, резина.
Свойства эластомеров:
Эластичность
Пластичность
Сократимость
Слайд 40Мышцы содержат
эластин +
коллаген
Придает армирующие свойства
Какова роль коллагена?
Придает армирующие свойства
Мышца
– это вязкоупругий элемент.
актин & миозин - сократительные белки
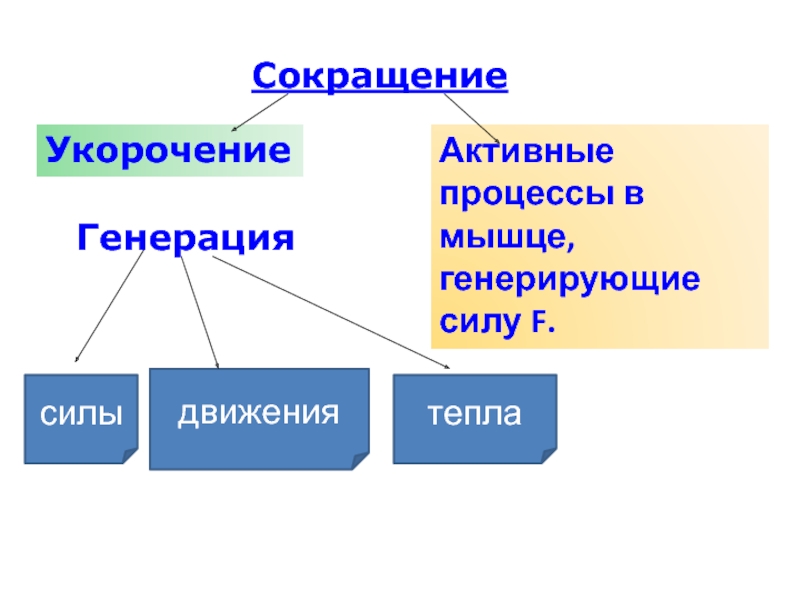
Слайд 41Сокращение
Укорочение
Генерация
Активные процессы в мышце, генерирующие силу F.
силы
движения
тепла
Слайд 42
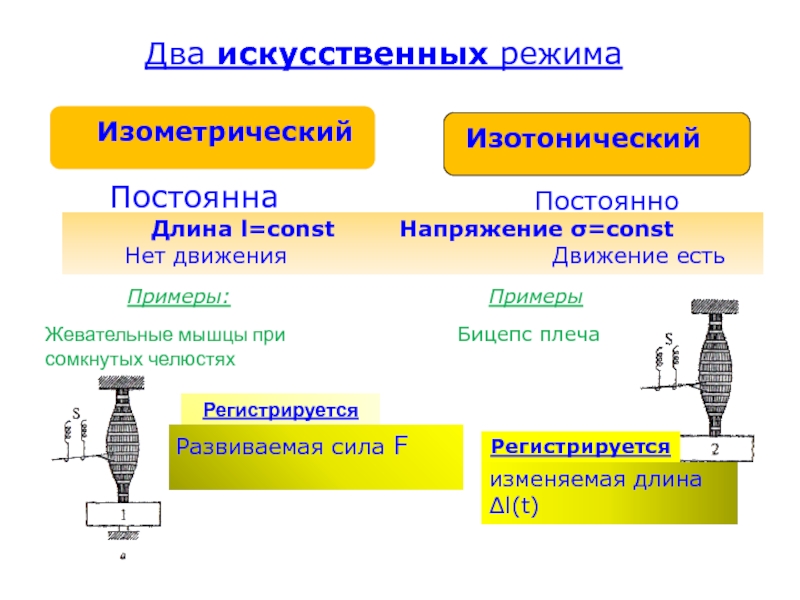
Два искусственных режима
Изометрический
Изотонический
Постоянна
Длина l=const Напряжение σ=const
Нет движения
Движение есть
Примеры:
Жевательные мышцы при
сомкнутых челюстях
Регистрируется
Развиваемая сила F
Постоянно
Примеры
Бицепс плеча
Регистрируется
изменяемая длина ∆l(t)
Слайд 43Уравнения Хилла
I уравнение Хилла
qx – предельное значение
выделившейся теплоты
x – укорочение.
Нобелевская
премия в 36 лет
II уравнение Хилла
P – нагрузка
v – скорость сокращения
P0 – максимальная нагрузка
Уравнения Хилла для изотонического режима
Хилл Арчибальд
Англ. Физиолог
1886-1977
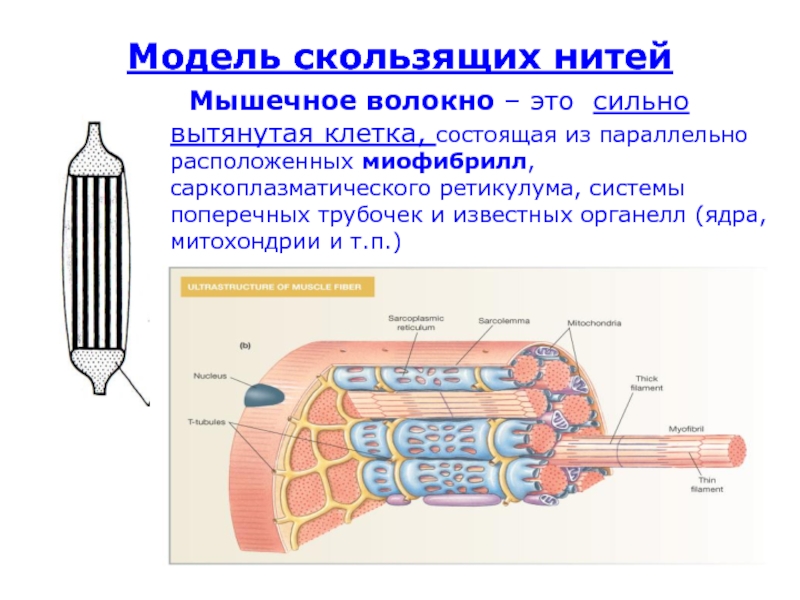
Слайд 44Модель скользящих нитей
Мышечное волокно – это сильно вытянутая клетка,
состоящая из параллельно расположенных миофибрилл, саркоплазматического ретикулума, системы поперечных трубочек
и известных органелл (ядра, митохондрии и т.п.)
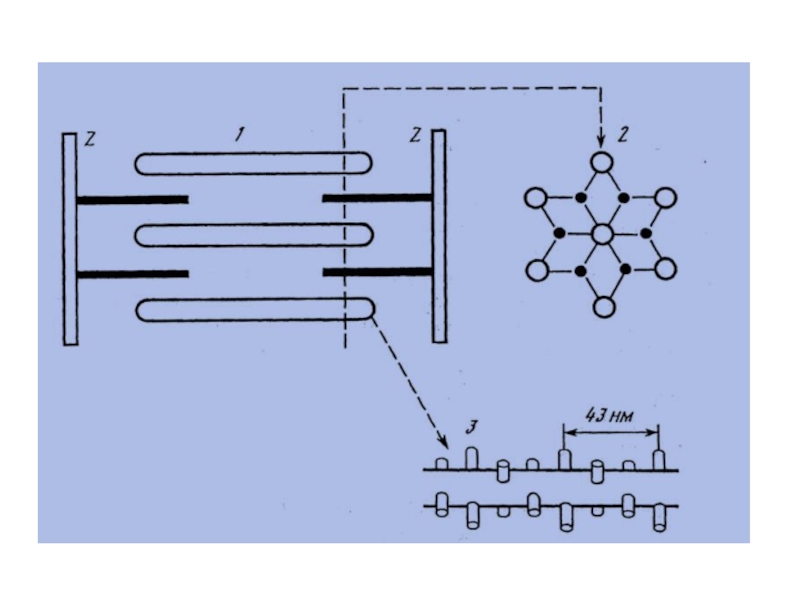
Слайд 45Миофибриллы состоят из саркомеров – элементарных сократительных единиц
Саркомер
Ультраструктура миофибриллы:
Саркомер –элементарная
сократительная единица мышечной клетки. Его длина 3,5 мкм.
Содержит параллельные
нити двух типов: толстые нити и тонкие нити.
Толстые нити состоят из миозина - очень длинный белок.
Тонкая нить состоит из актина, прикрепленного одним концом к Z – диску.
Слайд 47
Модель скользящих нитей
При умеренной деформации длина миозиновых и актиновых
нитей постоянна, а длина саркомера уменьшается, так как нити скользят
друг относительно друга при помощи поперечных мостиков.
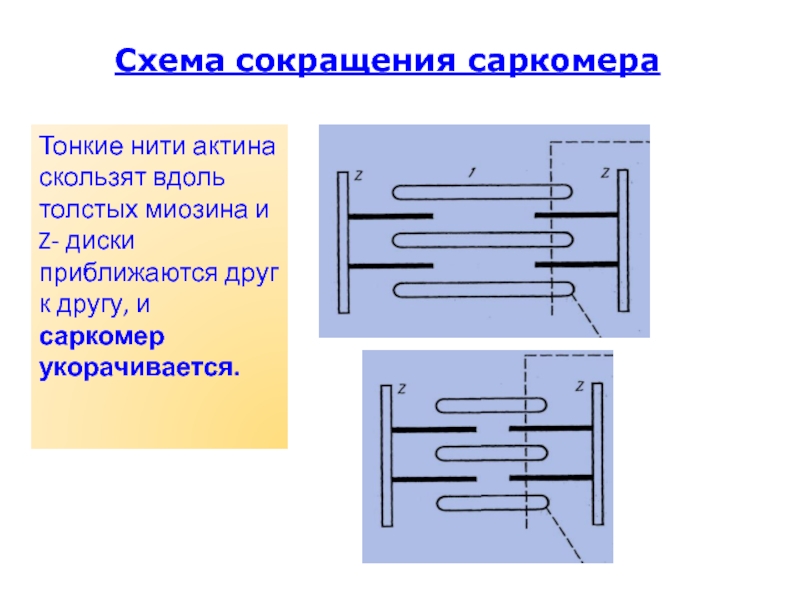
Слайд 48Схема сокращения саркомера
Тонкие нити актина скользят вдоль толстых
миозина и Z- диски приближаются друг к другу, и саркомер
укорачивается.
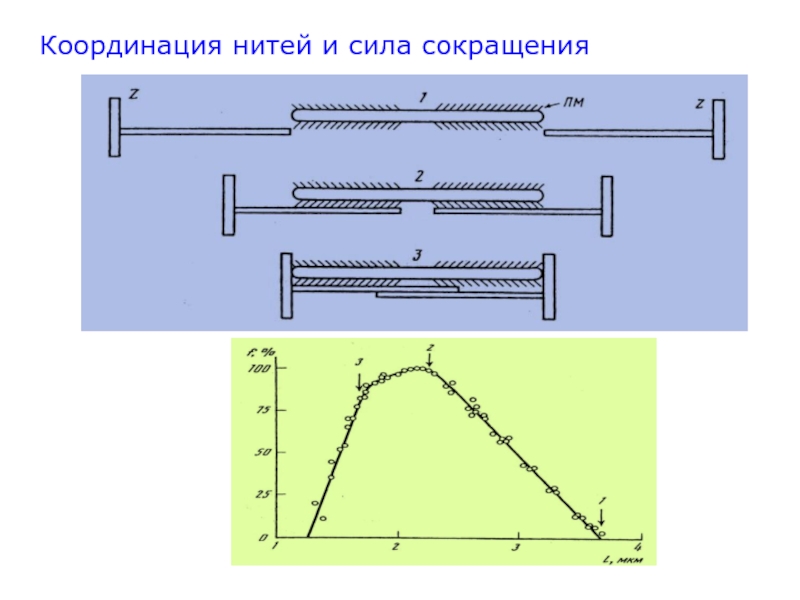
Слайд 49Координация нитей и сила сокращения
Слайд 50
Гидролиз АТФ и энергетика сокращения
АТФ – непосредственный источник
энергии
для сокращения
Без АТФ поперечные мостики лишены энергии и актиновые
нити не могут скользить вдоль миозиновых, сокращения мышцы не происходит.
При активизации мышцы происходит усиленный гидролиз АТФ и энергетический обмен возрастает в 100-1000 раз по сравнению с покоем.
Запасы АТФ в мышцах ничтожны (их хватает на 2-3 секунды работы). Поэтому должен происходить постоянный ресинтез АТФ с той же скоростью, с какой он расходуется.
В качестве источников энергии при этом используются углеводы, жиры и белки.
При гидролизе АТФ выделяется 10 ккал/кг свободной энергии
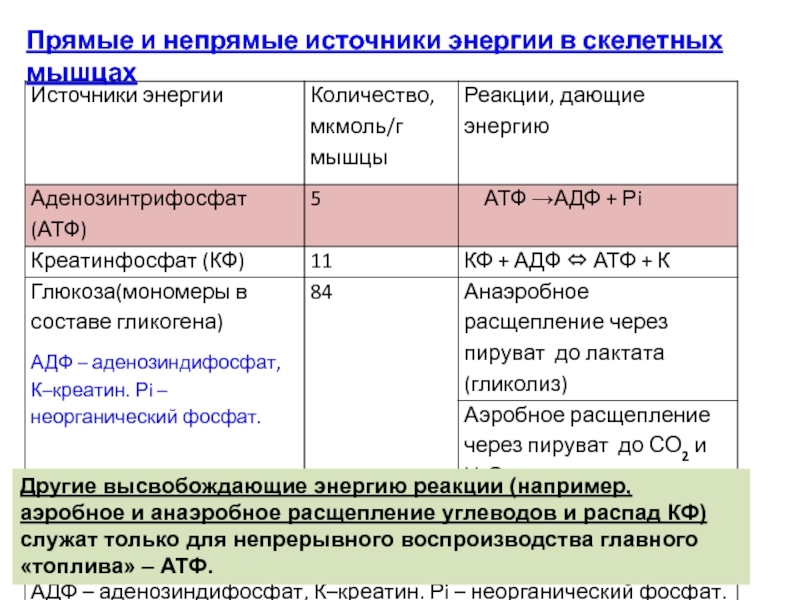
Слайд 51
Прямые и непрямые источники энергии в скелетных мышцах
Другие
высвобождающие энергию реакции (например, аэробное и анаэробное расщепление углеводов и
распад КФ) служат только для непрерывного воспроизводства главного «топлива» – АТФ.
Слайд 52
Электромеханическое
сопряжение в мышцах
- это цикл последовательных процессов,
начинающийся с возникновения ПД на клеточной мембране и заканчивающийся сократительным
ответом мышцы.
Слайд 53
Способность актомиозинового комплекса к сокращению зависит от присутствия в
среде ионов Са2+
Наличие ионов Са2+ => расщепление АТФ =>
сокращение миофибрилл
Удаление ионов Са2+ => поступление АТФ => расслабление миофибрилл
Поступление и удаление ионов Са2+ осуществляет система активного транспорта - Са2+ - насос.
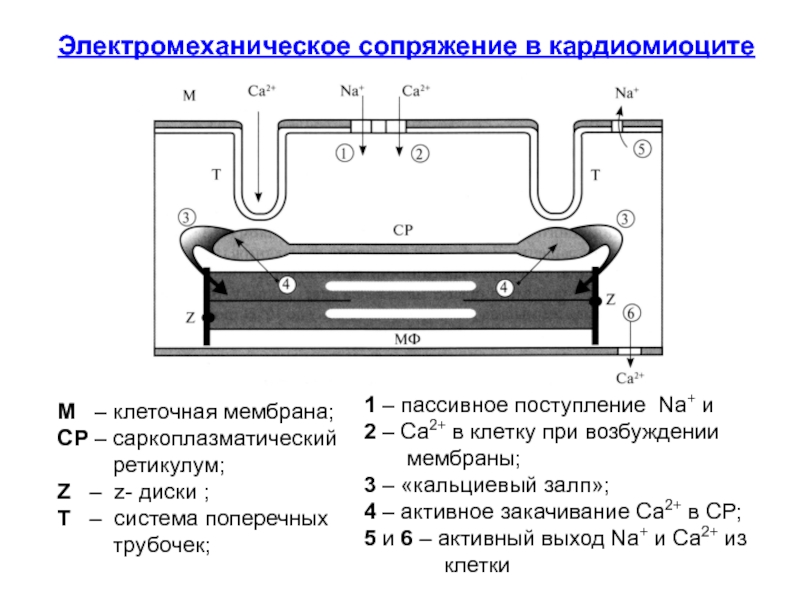
Слайд 54Электромеханическое сопряжение в кардиомиоците
М – клеточная мембрана;
СР – саркоплазматический
ретикулум;
Z – z- диски ;
Т
– система поперечных
трубочек;
1 – пассивное поступление Na+ и
2 – Ca2+ в клетку при возбуждении
мембраны;
3 – «кальциевый залп»;
4 – активное закачивание Ca2+ в СР;
5 и 6 – активный выход Na+ и Ca2+ из
клетки






![Лекция 2
Биореология
Гидродинамика. Биофизика мышечных сокращений Вязкость зависит от температурыПрироды жидкостиФормы молекулКинематическая вязкость[Ст] = стоксТекучесть-величина обратная вязкостиt ηДля жидкостей Вязкость зависит от температурыПрироды жидкостиФормы молекулКинематическая вязкость[Ст] = стоксТекучесть-величина обратная вязкостиt ηДля жидкостей](/img/thumbs/2dad6f838e795f459f996c9261f8e5fd-800x.jpg)