Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 2 НЕСТРОГОЕ ОПРЕДЕЛЕНИЕ АЛГОРИТМА. СВОЙСТВА АЛГОРИТМОВ
Содержание
- 1. Лекция 2 НЕСТРОГОЕ ОПРЕДЕЛЕНИЕ АЛГОРИТМА. СВОЙСТВА АЛГОРИТМОВ
- 2. Алгоритмодно из фундаментальных понятий информатикиПредмет теории алгоритмов
- 3. Алгоритм Евклида
- 4. нестрогое определениеалгоритм – точно определенная последовательность действий,
- 5. Cуществует несколько подходов к определению понятия алгоритма
- 6. Первый подход (Колмогоров)Алгоритм - это предписание,
- 7. Американский ученый Д. Кнут1. Конечность. Алгоритм должен
- 8. По определению А.П. Ершоваалгоритм - это понятное
- 9. Свойства алгоритма по Ершову: Дискретность. Точность. Понятность. Результативность. Массовость.
- 10. Второй подход (А.Черч, Д.Гильберт, П.С.Новиков) Эти ученые
- 11. Третий подход представляют А. Тьюринг и Э.Л.
- 12. ОпределениеАлгоритм - понятное и точное предписание исполнителю совершить последовательность действий, направленных на достижение поставленной цели
- 13. Исполнитель алгоритма– субъект или устройство, способные правильно
- 14. Способы представления алгоритмаГрафическийСловесныйНа алгоритмическом языке (или языке программирования).
- 15. Графический способБлок-схема - это ориентированный граф, указывающий
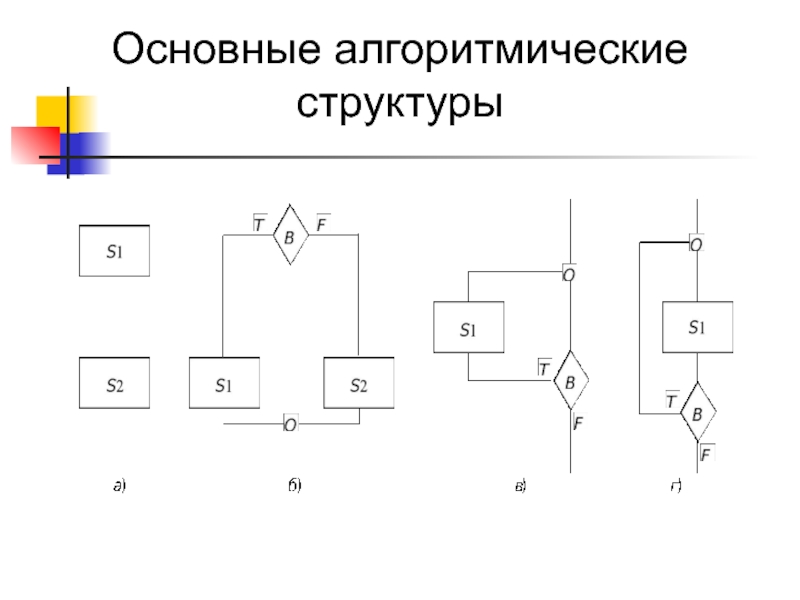
- 16. Основные алгоритмические структуры
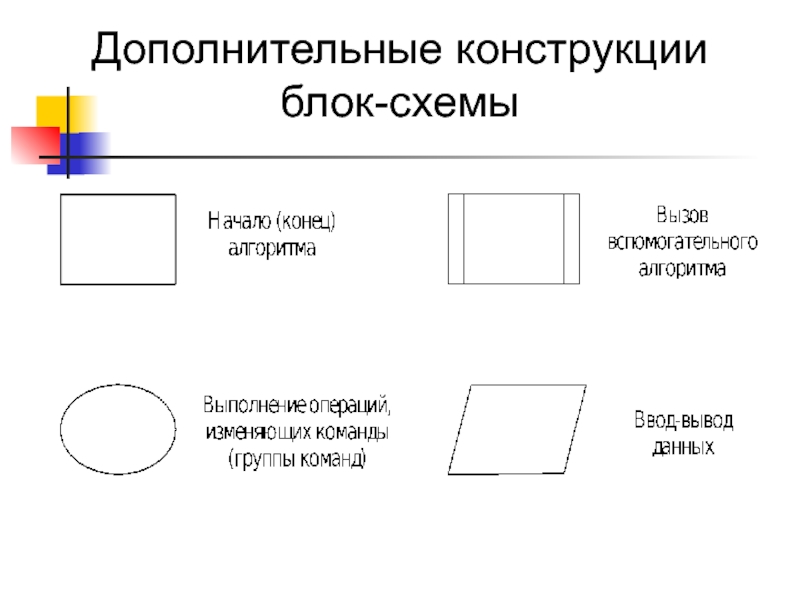
- 17. Дополнительные конструкции блок-схемы
- 18. Структурный подходУправляющие структурыСуперпозицияМетод нисходящего проектирования(метод детализации)
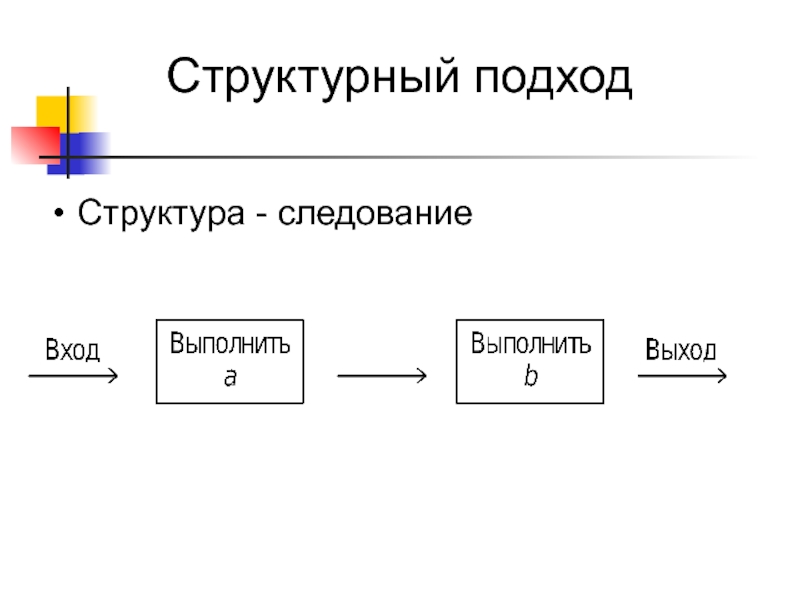
- 19. Структурный подходСтруктура - следование
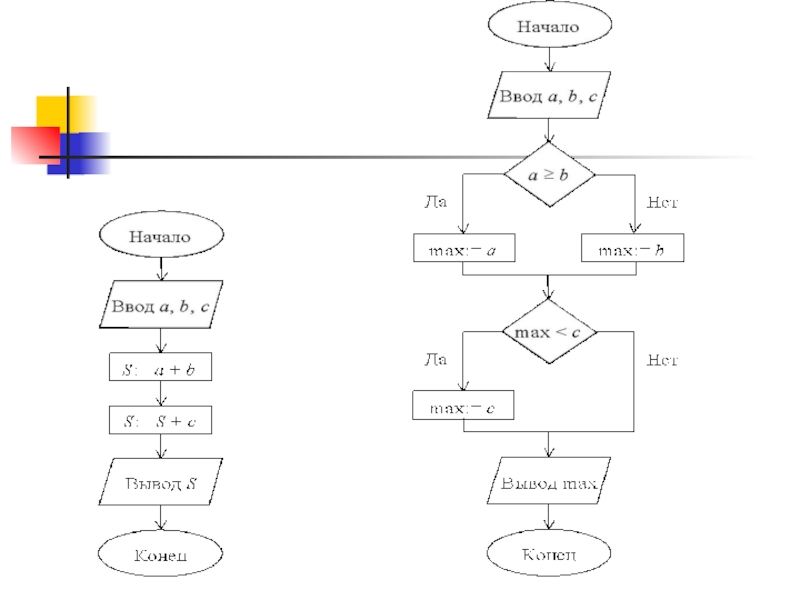
- 20. Структура - ветвление
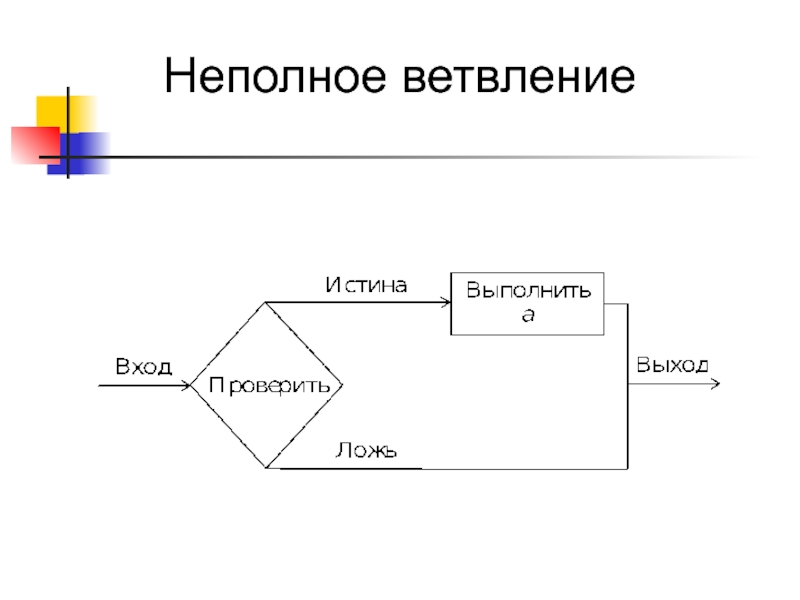
- 21. Неполное ветвление
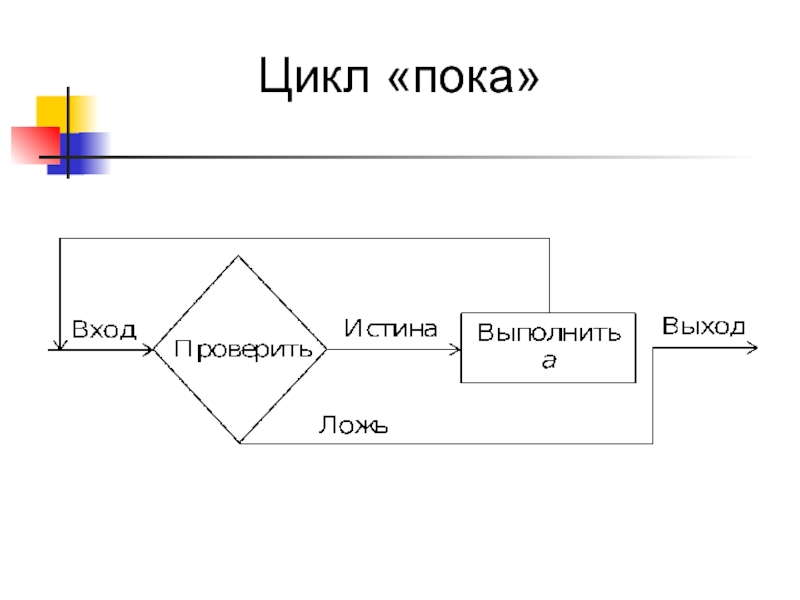
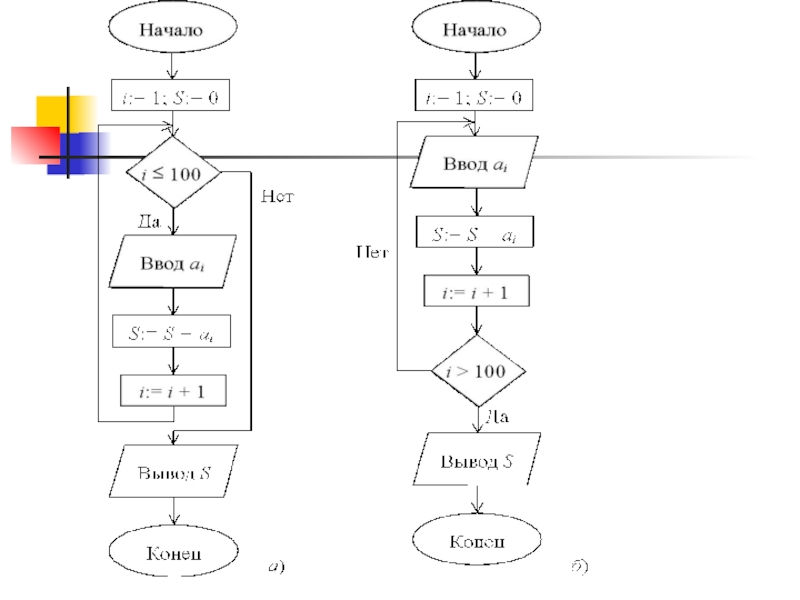
- 22. Цикл «пока»
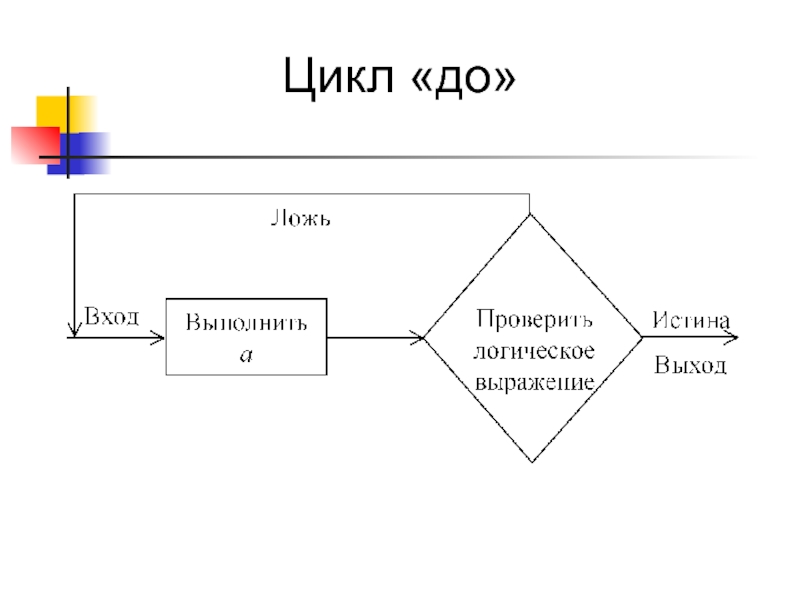
- 23. Цикл «до»
- 24. Структурная теоремаЛюбую схему алгоритма можно представить в
- 25. Слайд 25
- 26. Слайд 26
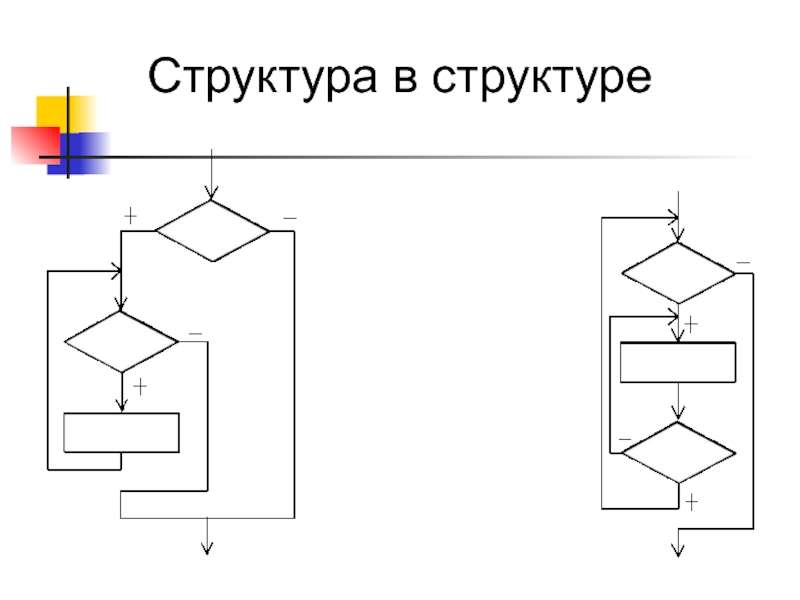
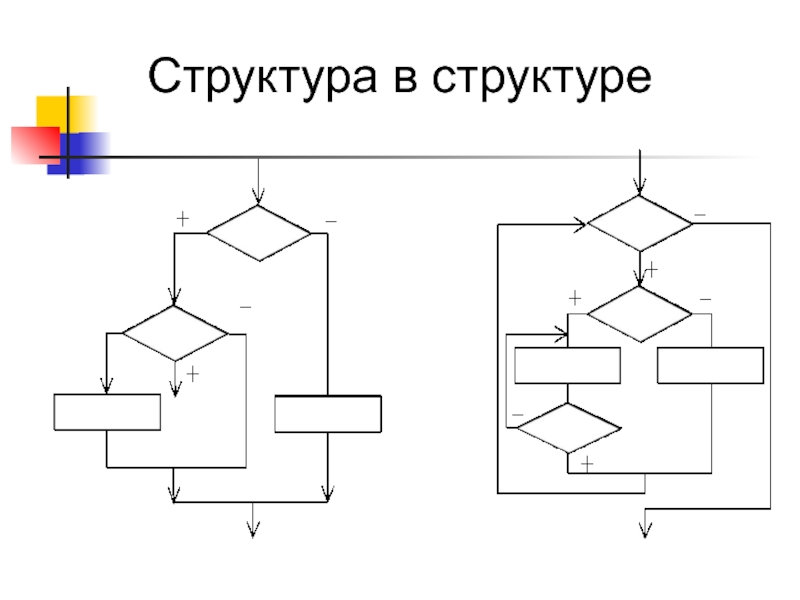
- 27. Структура в структуре
- 28. Структура в структуре
- 29. Сложность алгоритмов
- 30. Критерии эффективности алгоритмаобъем памяти компьютера для размещения
- 31. Временная сложность«эффективным» понимается алгоритм, обеспечивающий наиболее быстрое получение результата,
- 32. МетодологияВремя работы алгоритма удобно выражать в виде
- 33. Опр.Временная сложность алгоритма - это функция, которая
- 34. Опр.Полиномиальным называется алгоритм, временная сложность которого выражается
- 35. Оценка времени
- 36. Алгоритм оценки
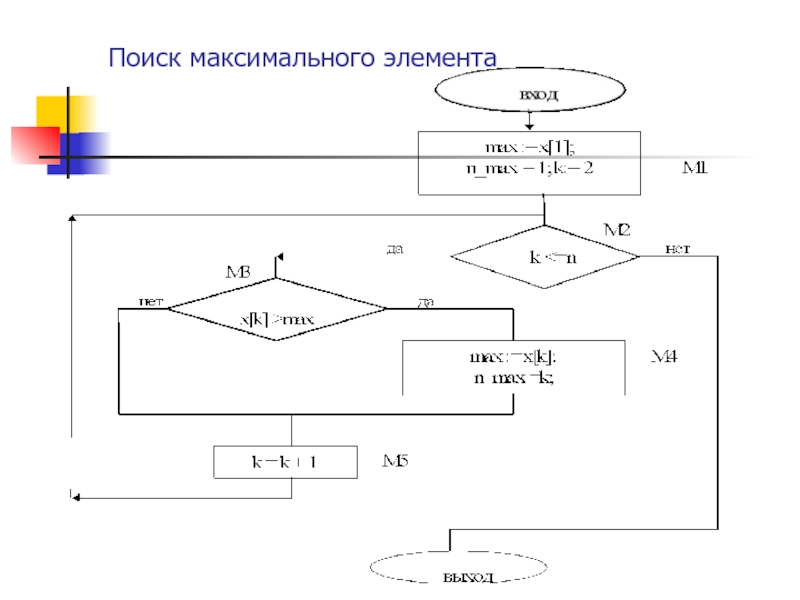
- 37. Поиск максимального элемента
- 38. Подсчет кол-ва операцийМ1=1, М2=n, M3=n-1M4=А (Амин=0, Амакс=n-1)M5=n-1
- 39. ПримерыРешение системы линейных уравненийСортировка массивовРешение задачи Коши
- 40. Рекурсивные алгоритмыПримеры рекурсийF(n) = F(n-1) или наоборот
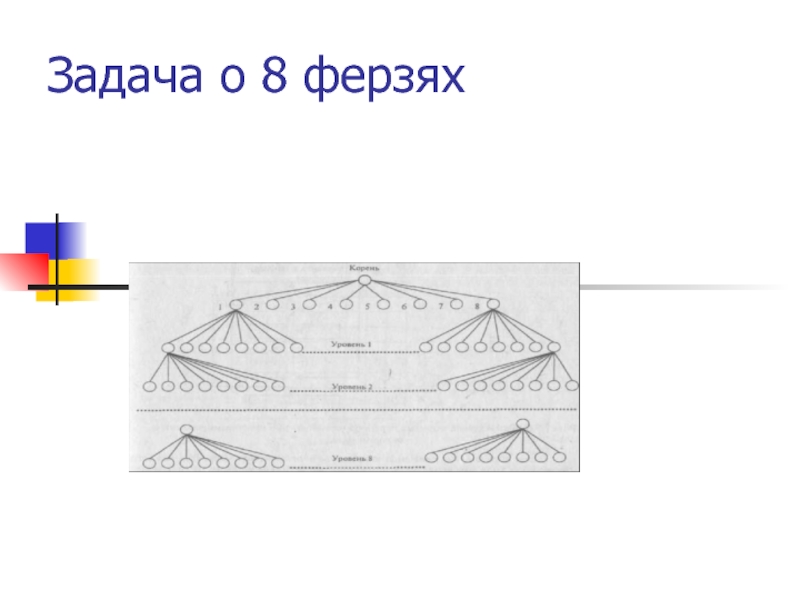
- 41. Задача о 8 ферзях
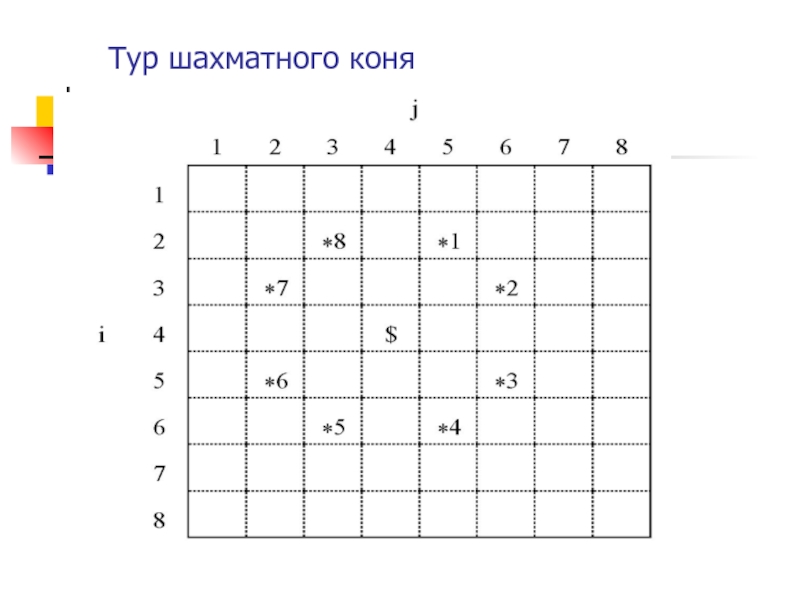
- 42. ЗадачиТур шахматного коняРешение физических задач
- 43. Тур шахматного коня
- 44. Контрольные вопросы1. Чем определяются свойства алгоритмов «дискретность», «определенность»,
- 45. Скачать презентанцию
Алгоритмодно из фундаментальных понятий информатикиПредмет теории алгоритмов - общие подходы к решению проблем обработки дискретной информации
Слайды и текст этой презентации
Слайд 2Алгоритм
одно из фундаментальных понятий информатики
Предмет теории алгоритмов - общие подходы
к решению проблем обработки дискретной информации
Слайд 3Алгоритм Евклида
НОД(n, m)
1. r=m mod n (остаток от
деления)2. Замена m:=n, n:= r
3. Если n<>0, то переход на п.1
(иначе) остановка: ответ : m
Слайд 4нестрогое определение
алгоритм – точно определенная последовательность действий, обеспечивающая решение задач
определенного класса для указанного класса исходных данных.
Слайд 6
Первый подход (Колмогоров)
Алгоритм - это предписание, обладающее следующими свойствами:
Дискретность алгоритма
Детерминированность.
Элементарность шагов
Направленность.
Массовость.
Слайд 7Американский ученый Д. Кнут
1. Конечность. Алгоритм должен заканчиваться через конечное
число шагов.
2. Определенность. Каждый шаг алгоритма должен быть точно определен.
3.
Ввод. Алгоритм имеет некоторое число входных данных.4. Выход. Алгоритм имеет одну или несколько выходных величин.
Эффективность. Все шаги алгоритма должны быть достаточно просты, чтобы их можно было выполнить за конечный отрезок времени
Слайд 8По определению А.П. Ершова
алгоритм - это понятное и точное предписание
исполнителю совершить последовательность действий, направленных на достижение поставленной цели или
на решение поставленной задачи.Слайд 9Свойства алгоритма по Ершову:
Дискретность.
Точность.
Понятность.
Результативность.
Массовость.
Слайд 10Второй подход (А.Черч, Д.Гильберт, П.С.Новиков)
Эти ученые определили алгоритм
через класс вычислимых (общерекурсивных) функций. Они все проблемы разделили на
алгоритмически разрешимые и неразрешимые.Слайд 11Третий подход представляют А. Тьюринг и Э.Л. Пост
Ими были
описаны машины, с помощью которых можно было реализовать любой алгоритм.
Слайд 12Определение
Алгоритм - понятное и точное предписание исполнителю совершить последовательность действий,
направленных на достижение поставленной цели
Слайд 13Исполнитель алгоритма
– субъект или устройство, способные правильно воспринимать описание алгоритма
и выполнять содержащиеся в нем действия.
Совокупность допустимых команд образует систему
команд исполнителя (СКИ )Слайд 14Способы представления алгоритма
Графический
Словесный
На алгоритмическом языке (или языке программирования).
Слайд 15Графический способ
Блок-схема - это ориентированный граф, указывающий порядок исполнения команд
алгоритма; вершины такого графа могут быть одного из трех типов
Слайд 18Структурный подход
Управляющие структуры
Суперпозиция
Метод нисходящего проектирования
(метод детализации)
Слайд 24Структурная теорема
Любую схему алгоритма можно представить в виде композиции вложенных
блоков begin и end, условных операторов if, then, else, циклов
с предусловием (while) и может быть дополнительных логических переменныхСлайд 30Критерии эффективности алгоритма
объем памяти компьютера для размещения данных и программы
время
центрального процессора по обработке этих данных
Слайд 31Временная сложность
«эффективным» понимается алгоритм, обеспечивающий наиболее быстрое получение результата,
Слайд 32Методология
Время работы алгоритма удобно выражать в виде функции от одной
переменной, характеризующей «размер» конкретной задачи, т.е. объем входных данных, необходимых
для ее решенияСлайд 33Опр.
Временная сложность алгоритма - это функция, которая каждой входной длине
слова ставит в соответствие максимальное время, затрачиваемое алгоритмом на ее
решение.Слайд 34Опр.
Полиномиальным называется алгоритм, временная сложность которого выражается некоторой полиномиальной функцией
размера задачи.
Алгоритмы, временная сложность которых не поддается подобной оценке, называются
экспоненциальными.Слайд 40Рекурсивные алгоритмы
Примеры рекурсий
F(n) = F(n-1) или наоборот F(n)=F(n+1)
n! = n*(n-1)!
|Нод(a,a-b),
если a>bНод(a,b)= |Нод(a-b, b), если b>a
| a, если a=b
Слайд 44Контрольные вопросы
1. Чем определяются свойства алгоритмов «дискретность», «определенность», «понятность», «результативность», «массовость»?
2. Кто (что) может быть исполнителем алгоритма?
3. Какова причина в
необходимости формализации понятия «алгоритм»?4. Каковы возможные подходы к определению понятия алгоритм?