Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 3
Содержание
- 1. Лекция 3
- 2. нестрогое определениеалгоритм – точно определенная последовательность действий,
- 3. Формализация понятия алгоритмСуществует большое количество задач, вызывающих
- 4. Главной цельюформализации понятия алгоритма является решение проблемы
- 5. Второй целью– является определение элементарного шага алгоритма
- 6. Третьей цельюстрогого определения понятия «алгоритм» является выбор
- 7. два класса задач1. вычисление значений функций2. распознавание принадлежности объекта заданному множеству
- 8. определениеФункция называется вычислимой, если существует алгоритм, вычисляющий ее значение.
- 9. определениеМножество называется разрешимым, если имеется алгоритм, позволяющий
- 10. Второй подход (А.Черч, Д.Гильберт, П.С.Новиков) Эти ученые
- 11. Третий подход представляют А. Тьюринг и Э.Л.
- 12. Тезис Черча-ТьюрингаЛюбое разумное определение алгоритма, которое может
- 13. Контрольные вопросы1. Зачем нужны булевы функции?2. Почему можно
- 14. Проблема А – множество элементов информацииВ – другое множествоФ – функция преобразования
- 15. Функция преобразованияD1D2FABФ
- 16. Ф = D1*F*D2Нужно строить три функциональных преобразователяПример(a1,
- 17. Определение Обозн.: (0,1)n = (x1,x2,…,xn) – вектор
- 18. Функции от одной переменнойF: X ->Y,
- 19. Функции от двух переменных (16 шт)
- 20. Теорема 1 Любая двоичная функция может быть
- 21. ОпределениеФункционально полным набором (базисом) будем называть такое
- 22. Определение Представление булевой функции в форме дизъюнкции:
- 23. Конъюктивная нормальная функция. Совершенная форма КНФОпределяются аналогично ДНФ и СДНФ (симметрично).
- 24. Теорема 2 Представление булевых функций
- 25. Формы представления булевских функцийТабличная (таблица истинности)аналитическая записьсемантическое деревобинарная диаграмма решения
- 26. РеализацияФизические устройства дискретного отображения 0 и 1 -- это ключ-реле (переключатели)
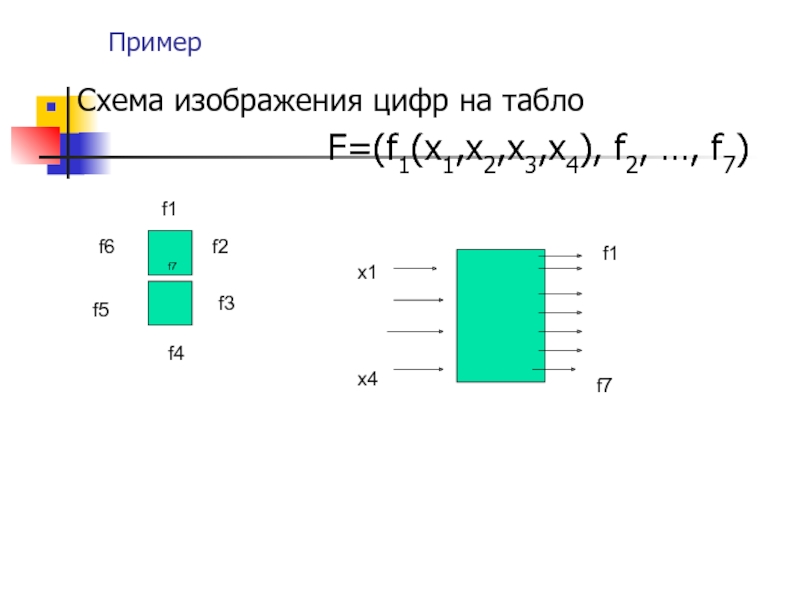
- 27. ПримерСхема изображения цифр на табло
- 28. МинимизацияМетод КвайнаФункция представляется в СДНФ и к
- 29. Пороговая логика Пример формального нейронаY=1, если ∑ xi*wi ≥ P, где P – пороговое значение,иначе У=0x1x2w1w2y
- 30. ВыводОбработку дискретной информации можно свести к построению
- 31. Скачать презентанцию
нестрогое определениеалгоритм – точно определенная последовательность действий, обеспечивающая решение задач определенного класса для указанного класса исходных данных.
Слайды и текст этой презентации
Слайд 2нестрогое определение
алгоритм – точно определенная последовательность действий, обеспечивающая решение задач
определенного класса для указанного класса исходных данных.
Слайд 3Формализация понятия алгоритм
Существует большое количество задач, вызывающих трудности создания алгоритма
их решения или требующих значительного упрощения процедур их решения или
расширения области применения известных алгоритмов и др. Существование таких задач требует формализовать понятие алгоритма. При этом выделяют 2 проблемы:возможно более строгое определение алгоритма, его свойства;
изучение теоретических моделей алгоритмов и исследование проблемы алгоритмической разрешимости.
Слайд 4Главной целью
формализации понятия алгоритма является решение проблемы алгоритмической разрешимости различных
математических задач, т.е. получение ответа на вопрос, существует ли алгоритм
решения указанного класса задач.
Слайд 6Третьей целью
строгого определения понятия «алгоритм» является выбор наиболее эффективного алгоритма
из нескольких возможных с теоретической и практической точек зрения
Слайд 7два класса задач
1. вычисление значений функций
2. распознавание принадлежности объекта заданному
множеству
Слайд 9определение
Множество называется разрешимым, если имеется алгоритм, позволяющий для любого объекта
определить, принадлежит он данному множеству или нет.
Слайд 10Второй подход (А.Черч, Д.Гильберт, П.С.Новиков)
Эти ученые определили алгоритм
через класс вычислимых (общерекурсивных) функций. Они все проблемы разделили на
алгоритмически разрешимые и неразрешимые.
Слайд 11Третий подход представляют А. Тьюринг и Э.Л. Пост
Ими были
описаны машины, с помощью которых можно было реализовать любой алгоритм.
Слайд 12Тезис Черча-Тьюринга
Любое разумное определение алгоритма, которое может быть предложено в
будущем, окажется эквивалентным уже известным определениям.
Слайд 13Контрольные вопросы
1. Зачем нужны булевы функции?
2. Почему можно автоматизировать процесс обработки
информации?
3. Какова причина в необходимости формализации понятия «алгоритм»?
4. Каковы возможные
подходы к определению понятия алгоритм? 
Слайд 16Ф = D1*F*D2
Нужно строить три функциональных преобразователя
Пример
(a1, а2,
а3, а4, а5 )
(в1, в2, в3)001, 010, 011, 100, 101 -> 01, 11, 00
Слайд 17Определение
Обозн.:
(0,1)n = (x1,x2,…,xn) – вектор из двоичных цифр
Функция f
: (0,1)n -> (0,1), сопоставляющая двоичным векторам двоичное число, называется
двоичной (или булевой) функцией.Основная задача – построение сложной булевой функции на основе простейших.
Слайд 18Функции от одной переменной
F: X ->Y, X = (0,1),
Y = (0,1)
f1(x) = 0
f2(x) = 1
f3(x) = x
f4(x)
= ¬x(две константы, тождественная и функция отрицания)
Слайд 19Функции от двух переменных (16 шт)
F: X*Y -> Z , X,Y,Z
= (0,1)f(x,y)= x^y; xvy; x =>y; xy; x+y; x↓y; x|y
конъюнкция, дизъюнкция, импликация (следование), эквивалентности, сложение по модулю 2 (ХОR), стрелка Пирса (НЕ-ИЛИ), штрих Шеффера (НЕ-И).
Слайд 20Теорема 1
Любая двоичная функция может быть представлена как суперпозиция трех
функций И, ИЛИ, НЕ.
(наз. Сложная функция или логическая формула)
Слайд 21Определение
Функционально полным набором (базисом) будем называть такое множество функций, суперпозицией
которых могут быть представлены любые булевы функции.
И, ИЛИ, НЕ –
являются базисом.
Слайд 22Определение
Представление булевой функции в форме дизъюнкции: F(x1,x2,…,xn) = K1 v
K2v ..v Kn , где каждый терм Кi представляет конъюнкцию
двоичных переменных, с отрицанием или без них, наз. дизъюнктивной нормальной функциейЕсли каждый конъюнкт содержит по одной из всех переменных (с отрицанием или без), то форма представления функции называется совершенной.
F(p,q,r) = ¬p¬q¬r v ¬pq¬r v p¬q¬r v pqr
Слайд 23Конъюктивная нормальная функция. Совершенная форма КНФ
Определяются аналогично ДНФ и СДНФ
(симметрично).
Слайд 24Теорема 2
Представление булевых функций в СДНФ, СКНФ
единственно.
Следствие
Всякая аналитическая запись функции может быть преобразована в
СДНФ или СКНФ.Алгоритм
Устраняем все операции, кроме И, ИЛИ, НЕ (свойства функций)
Преобразуем к одиночным отрицаниям (свойства функций).
Преобразуем к нормальной форме (свойства функции)
Слайд 25Формы представления булевских функций
Табличная (таблица истинности)
аналитическая запись
семантическое дерево
бинарная диаграмма решения
Слайд 26Реализация
Физические устройства дискретного отображения 0 и 1 -- это ключ-реле
(переключатели)
Слайд 28Минимизация
Метод Квайна
Функция представляется в СДНФ и к ней применяются все
возможные операции склеивания, а затем поглощения многократно.
Карта Карно
Двумерная табличная форма
с определенными манипуляциями.
Слайд 29Пороговая логика
Пример формального нейрона
Y=1, если ∑ xi*wi ≥ P, где
P – пороговое значение,
иначе У=0
x1
x2
w1
w2
y
Слайд 30Вывод
Обработку дискретной информации можно свести к построению булевой функции.
Вычисление любой
булевой функции можно автоматизировать.
Обработку дискретной информации можно автоматизировать на основе
алгоритма.
