Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 3. Ортогональные проекции плоскости
Содержание
- 1. Лекция 3. Ортогональные проекции плоскости
- 2. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ
- 3. СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ
- 4. Графические способы задания плоскости
- 5. Графические способы задания плоскости
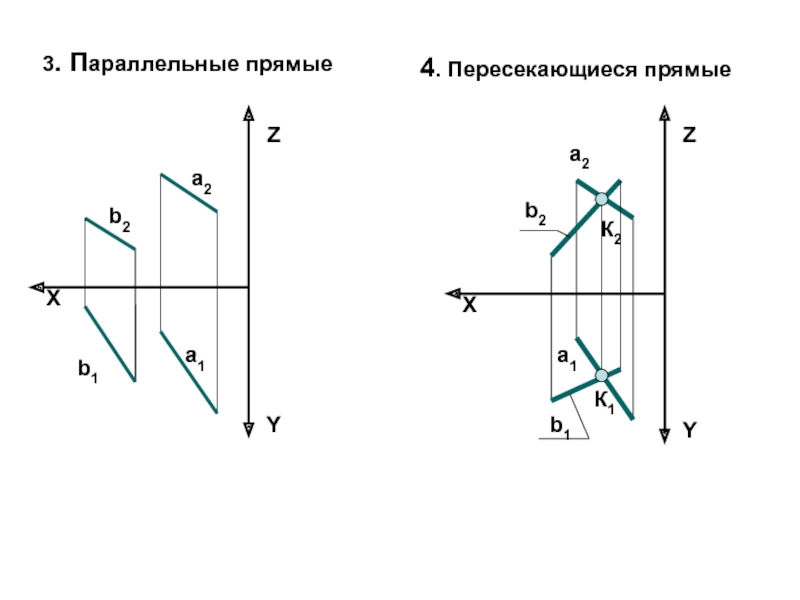
- 6. XZYа2а1b2b1XZYa2a1b2b13. Параллельные прямые4. Пересекающиеся прямыеК1К2
- 7. XZYА2А1В1C2C1В25. Плоская фигура
- 8. YZXaп1aП3aП2axayaz6. Следы плоскости – линии пересечения данной
- 9. ZXYYaП2aп1aП3axayazZXaп1aП3aП2axayazaayYxαyαZα
- 10. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ1. Относительно
- 11. ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ 1. Плоскости уровня –
- 12. ZXYYbп1bП3byYZXbп1bП3bybyФронтальная плоскость уровня b I| П2А1В1С1С2В2А2bΔАВС; IABCI=IA2B2C2IА3≡С3В3
- 13. ZXYYgП2gп1gxZXgп1gП2gxgПрофильная плоскость уровня П3Y
- 14. Особенности чертежа плоскостей уровняФигуры принадлежащие плоскостям уровня
- 15. 2. Проецирующие плоскости - это плоскости перпендикулярные плоскостям проекцийГоризонтально проецирующая плоскость ┴П1XYYaП2aП3ZXaп1aП2axaxZaп1aП3aYayyayayА1В1С1А2В2С2ΔАВС
- 16. Фронтально проецирующая плоскость ┴ П2ZXYYП2п1xYZXП2zП3П1П3zxА2В2С2А1В1С1fΔАВС
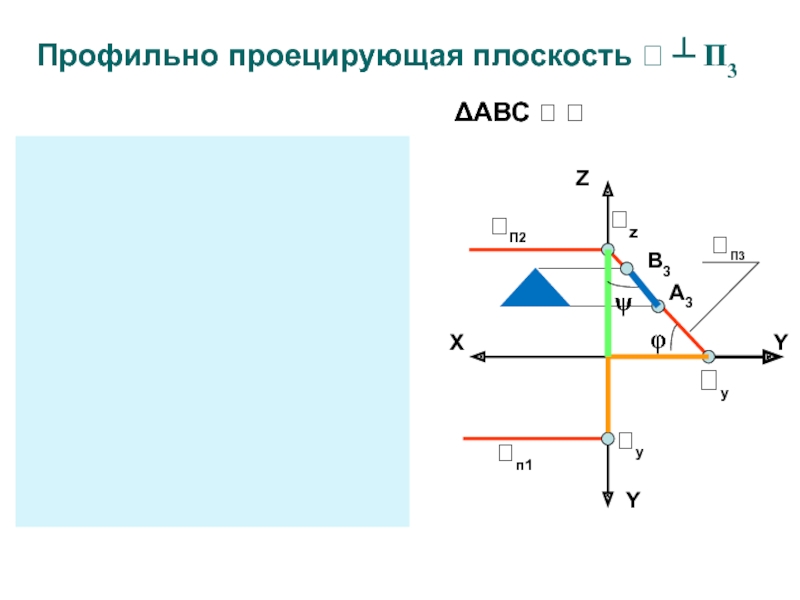
- 17. Профильно проецирующая плоскость ┴ П3ZXYYП2п1YZXп1П2П3П3zyzyyА3В3φψΔАВС
- 18. Фигуры принадлежащие проецирующим плоскостям на перпендикулярную плоскость
- 19. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯПлоскость общего положения
- 20. ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ ПЛОСКОСТИТочка принадлежит плоскости,
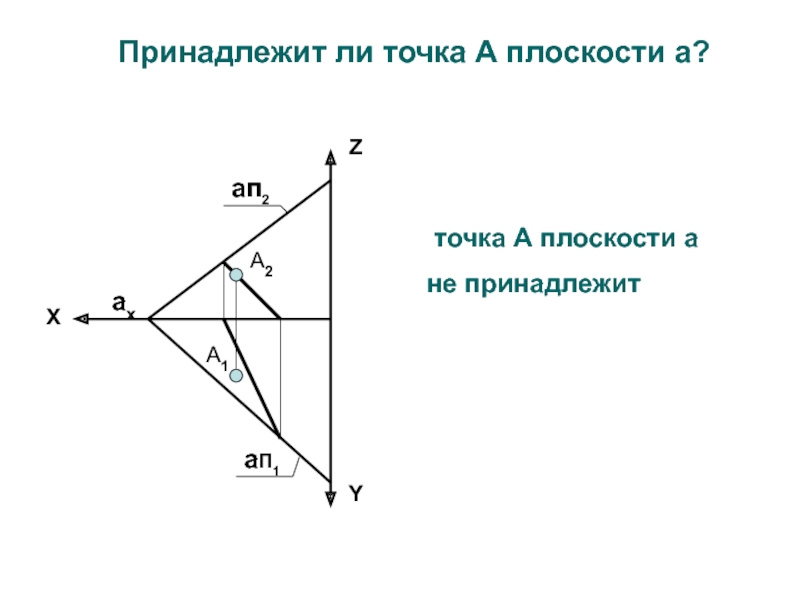
- 21. Принадлежит ли точка А плоскости a? А2А1aп2aП1axYZX точка А плоскости a не принадлежит
- 22. ОСОБЫЕ ЛИНИИ ПЛОСКОСТИЛИНИИ УРОВНЯ ПЛОСКОСТИ – линии
- 23. ZXaп1aП3aП2axayazaЛИНИИ УРОВНЯ ПЛОСКОСТИГоризонталь плоскостиY Горизонталь h парал-лельна горизонтальной плоскости проекций и принадлежит плоскости a
- 24. AН(h) горизонталь плоскости a;
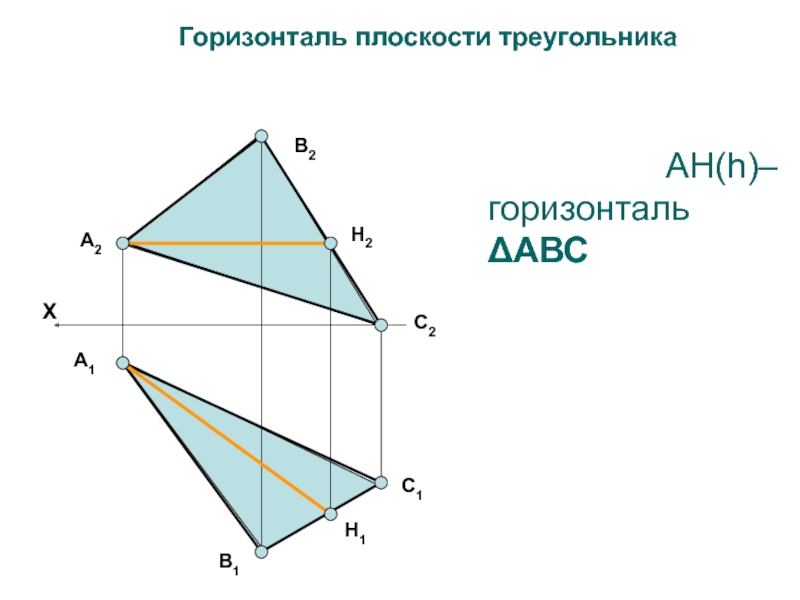
- 25. AH(h)– горизонталь ΔАВСГоризонталь плоскости треугольникаА2В2С2H2В1С1А1H1X
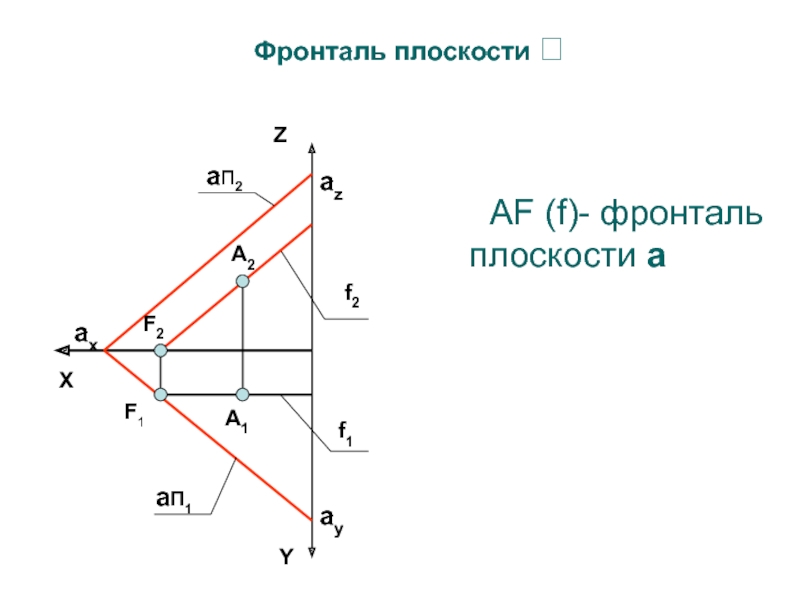
- 26. АF (f)- фронталь плоскости aФронталь плоскости aп2aП1YZaxА2А1f2f1F2F1Xazay
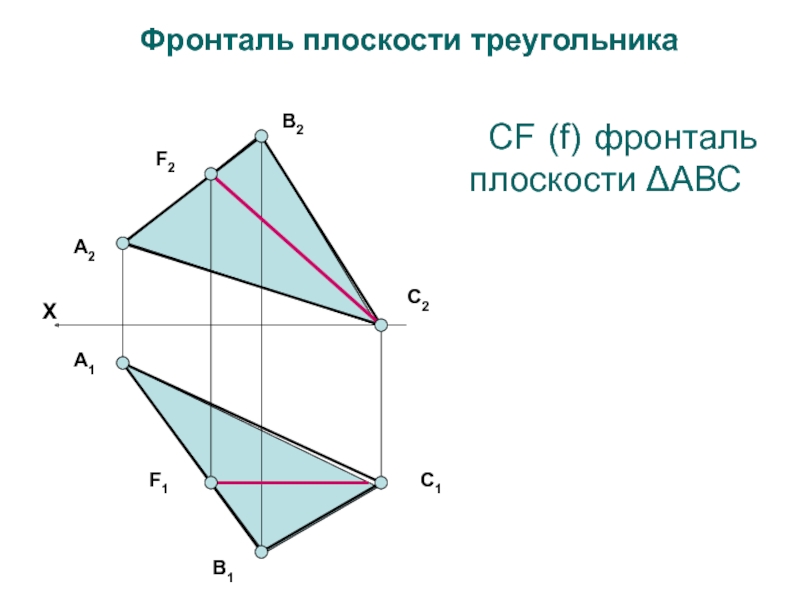
- 27. А2F2В2С2В1С1А1F1Фронталь плоскости треугольника СF (f) фронталь плоскости ΔАВСX
- 28. ZXaп1aП3aП2axayaza2. ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИК ПЛОСКОСТЯМ ПРОЕКЦИЙЛиния
- 29. 1. А1D1 ┴ А1H1 II П1.2. А1D1 ┴ αп1Линия скатаaп2aП1YXaxА2А1h2h1H2H1ayazD1D2
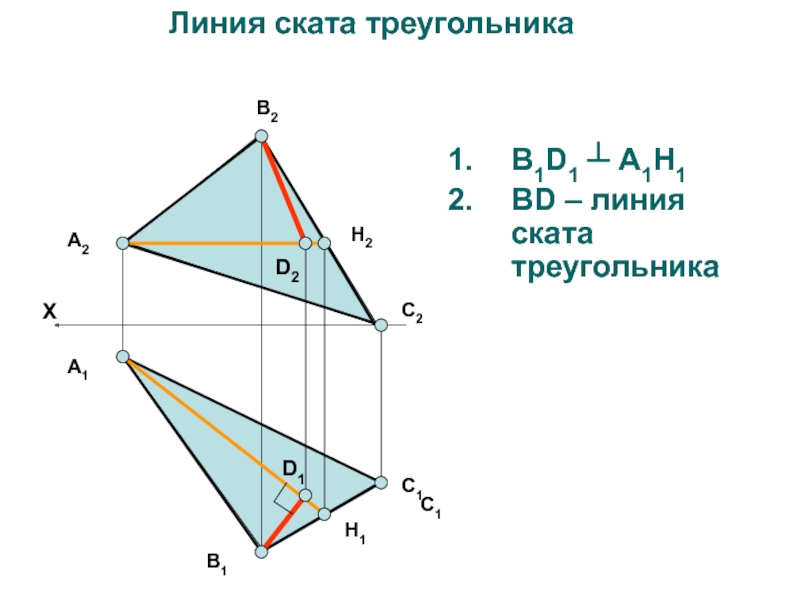
- 30. В1D1 ┴ А1H1ВD – линия ската треугольникаА2В2С2H2В1С1А1H1XЛиния ската треугольника D1D2С1
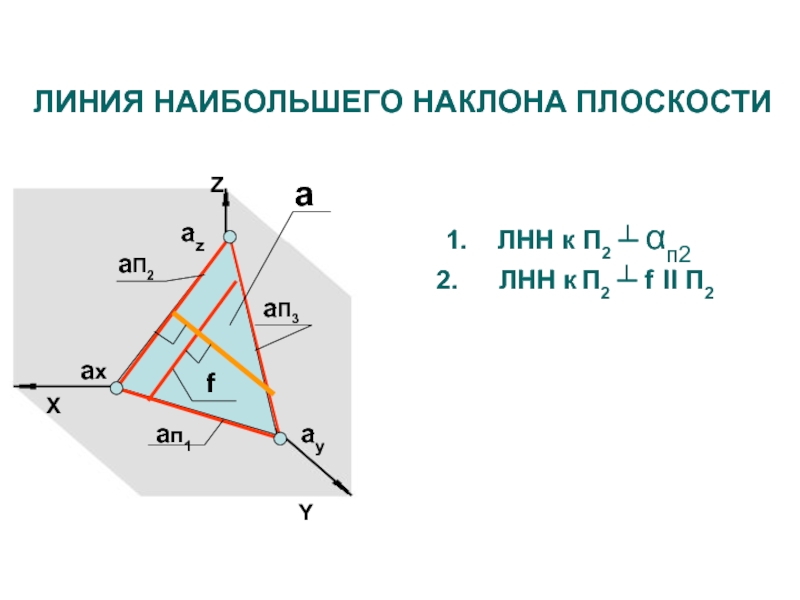
- 31. ZXaп1aП3aП2axayazaЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ1. ЛНН к П2 ┴ αп2ЛНН к П2 ┴ f II П2Yf
- 32. АЕ – ЛНН к П2
- 33. А2F2В2А1F1ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА плоскости ΔАВС к фронтальной
- 34. НОРМАЛЬ ПЛОСКОСТИ Нормаль плоскости n – линия перпендикулярная заданной плоскостиZXaп1aП3aП2axayazYan
- 35. Проекции нормали перпендикулярны про-екциям линий уровня плоскости
- 36. А2В2А1XВ1С1С2Через точку D провести перпендикуляр к плоскости
- 37. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ПЛОСКОСТЕЙ
- 38. ПАРАЛЛЕЛЬНЫЕ ПРЯМАЯ И ПЛОСКОСТЬ, ПЛОСКОСТИ
- 39. ПРЯМАЯ ПАРАЛЛЕЛЬНА ПЛОСКОСТИ, ЕСЛИ ОНА ПАРАЛЛЕЛЬНА ЛЮБОЙ
- 40. Через точку D провести прямую a параллельную Δ АВС и плоскость α(a∩b) параллельную Δ АВС
- 41. XYZA2B2A1C2C1B1a1a2D2D1a2 II B2C2a1 II B1C1a II BCa
- 42. Построить следы плоскости β, параллельной α и
- 43. ПРЯМАЯ ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ, ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИПРЯМАЯ ПЕРПЕНДИКУЛЯРНА
- 44. ЗадачаПостроить проекции нормали плоскости a, проходящей через точку С плоскости
- 45. C ααП1OXαп2 С2С1А2А1D1D2n1n2
- 46. Через точку D провести перпендикуляр к плоскости
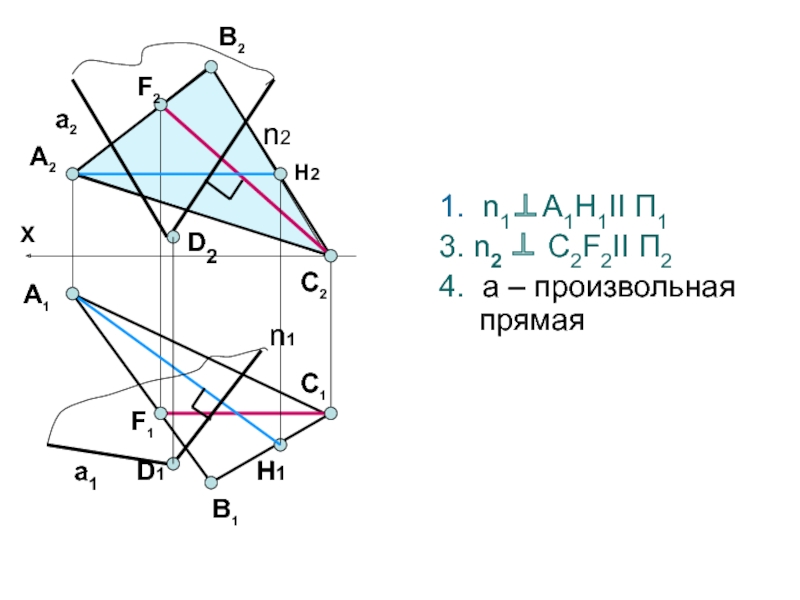
- 47. 1. n1А1Н1II П13. n2 С2F2II П24. а – произвольная прямаяА2F2В2А1F1XH2H1С1С2n2n1В1D2D1a2a1
- 48. ПЕРЕСЕКАЮЩИЕСЯ ПРЯМАЯ И ПЛОСКОСТЬ ПРЯМАЯ И ПЛОСКОСТЬ ПЕРЕСЕКАЮТСЯ, ЕСЛИ У НИХ ЕСТЬ ОДНА ОБЩАЯ ТОЧКА
- 49. Точка пересечения прямой и плоскости частного положения определяется на пересечении следа плоскости и проекции прямойXOa1а2п1п2К1К2XOa1а2п1п2К1К2
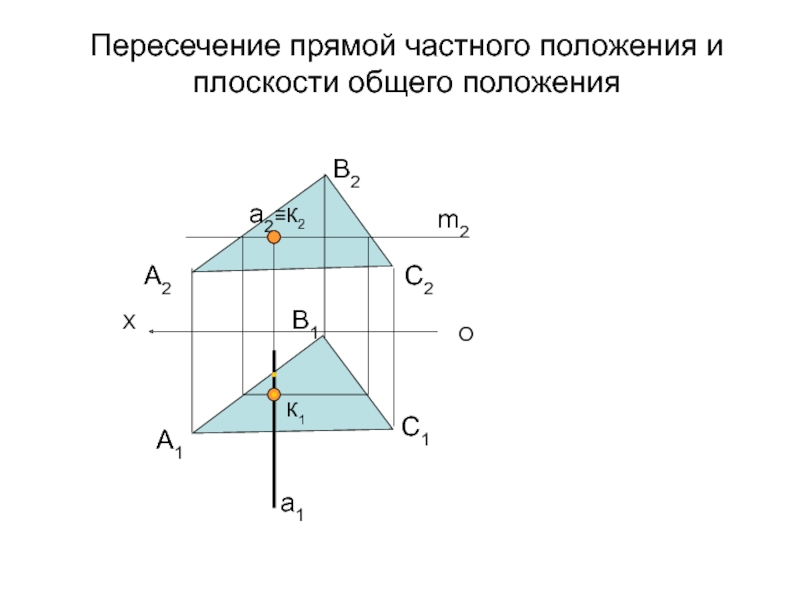
- 50. Пересечение прямой частного положения и плоскости общего положенияОXА2В2С2А1В1С1a1a2m2К1≡К2
- 51. Пересечение прямой общего положения и плоскости общего
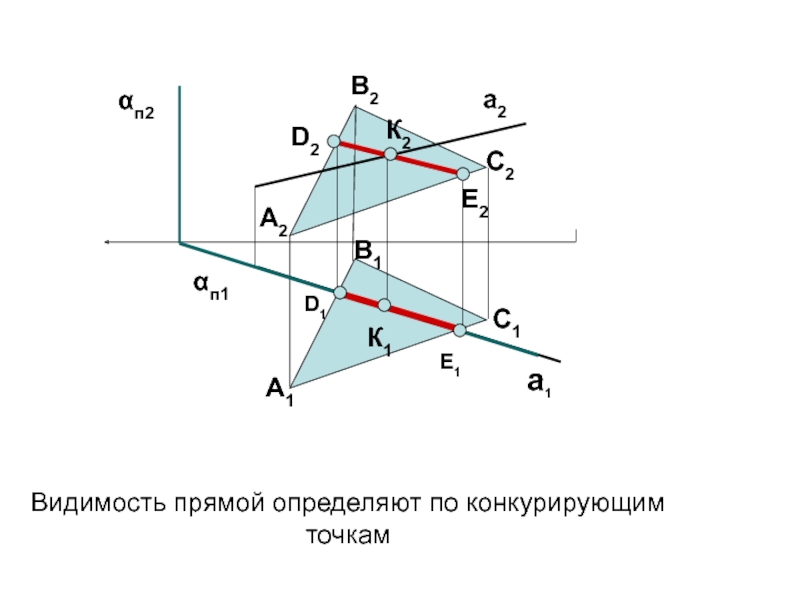
- 52. αп1C1Е2A2С2B2A1B1D1E1a1a2D2αп2К2К1Видимость прямой определяют по конкурирующим точкам
- 53. Видимость прямых определяют по конкурирующим точкам -которые
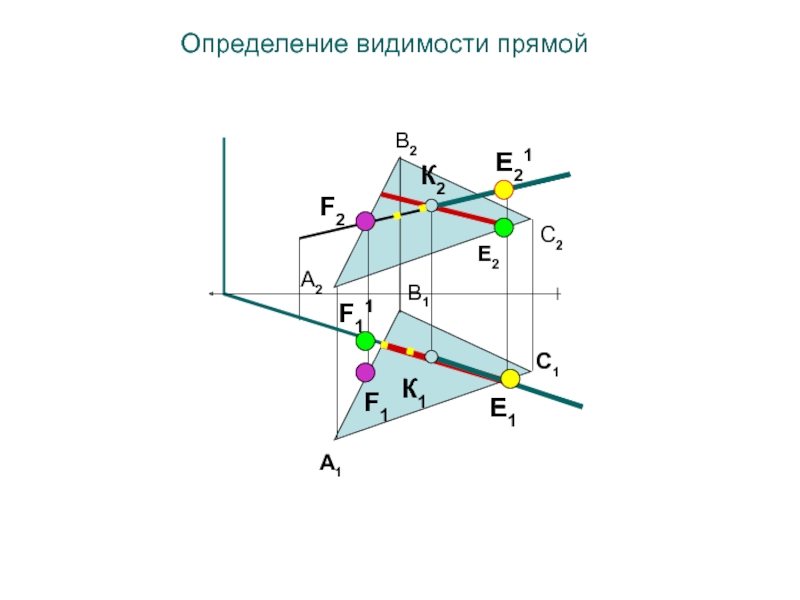
- 54. Определение видимости прямойЕ2F11E1F2Е21F1C1A2С2B2A1B1К1К2
- 55. ПЕРЕСЕКАЮЩИЕСЯ ПЛОСКОСТИ
- 56. 1. ПЛОСКОСТИ ПЕРЕСЕКАЮТСЯ, ЕСЛИ У НИХ ЕСТЬ
- 57. Линия пересечения фронтально-проецирующей плоскости и плоскости общего
- 58. Для построения линии пересечения плоскостей достаточно определить две общие точки заданных плоскостейПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ
- 59. ЗадачаПостроить линию пересечения треугольников ΔABC
- 60. Слайд 60
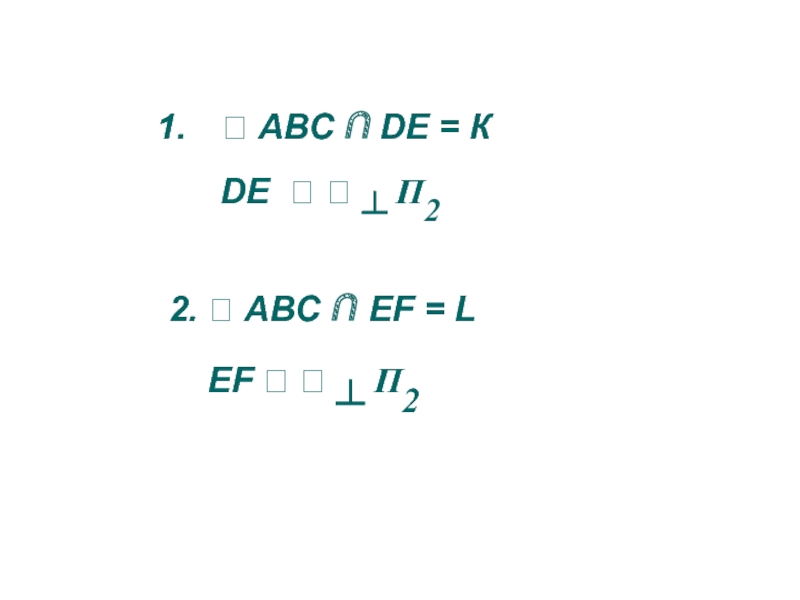
- 61. АВС ∩ DE = К
- 62. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯАВС ∩ α =
- 63. ОПРЕДЕЛЕНИЕ ВИДИМОСТИ СТОРОН ТРЕУГОЛЬНИКАВидимость определяем по конкурирующим
- 64. Слайд 64
- 65. Слайд 65
- 66. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 3. Ортогональные проекции плоскости
Способы задания плоскости
Плоскости общего и частного
положений
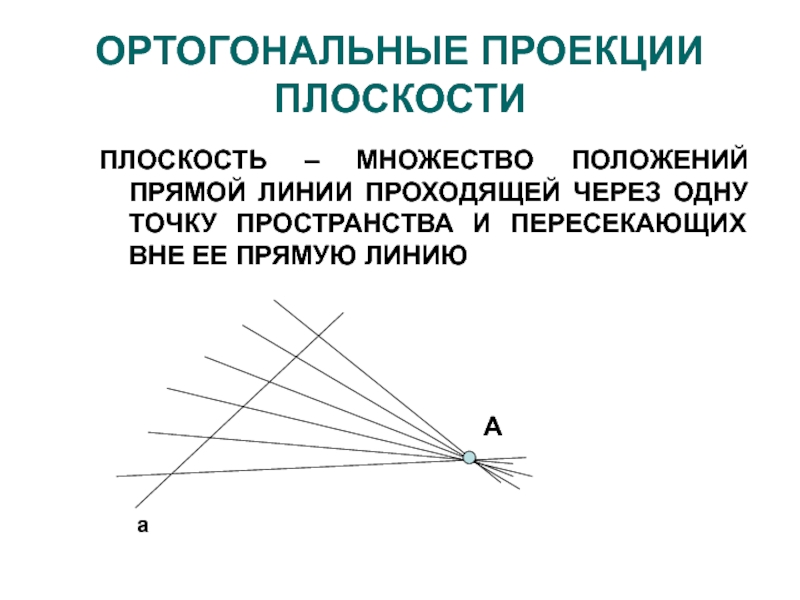
Слайд 2ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ
ПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ ЛИНИИ ПРОХОДЯЩЕЙ ЧЕРЕЗ
ОДНУ ТОЧКУ ПРОСТРАНСТВА И ПЕРЕСЕКАЮЩИХ ВНЕ ЕЕ ПРЯМУЮ ЛИНИЮ
A
a
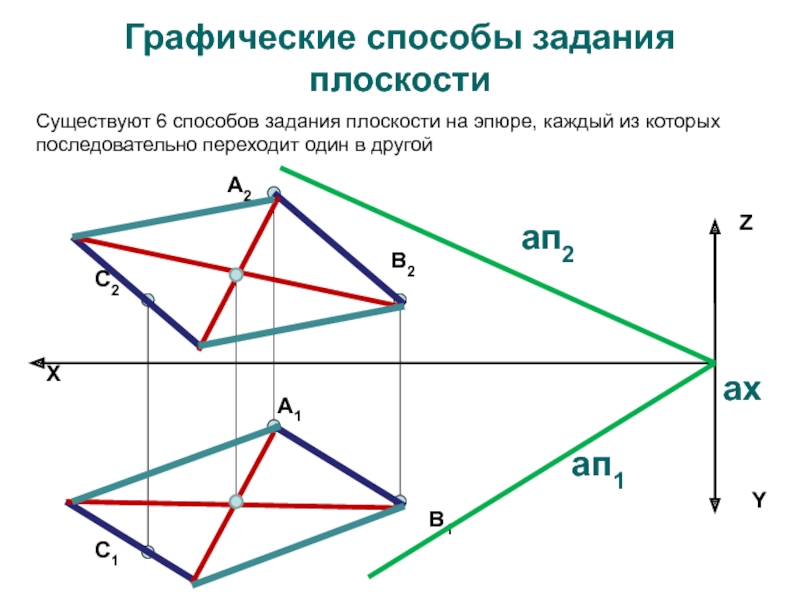
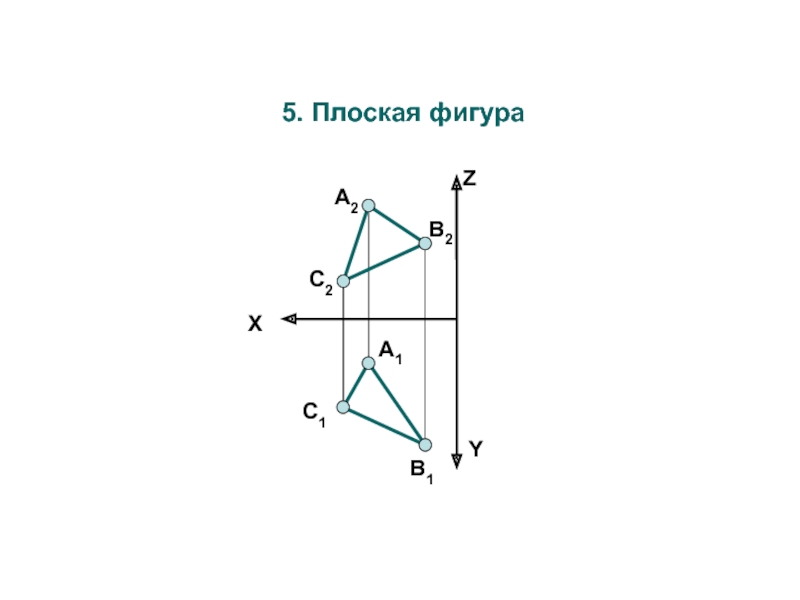
Слайд 4 Графические способы задания плоскости
X
Z
Y
А2
А1
В1
C2
C1
В2
Существуют 6 способов задания плоскости на эпюре, каждый из которых
последовательно переходит один в другойax
aп2
aп1
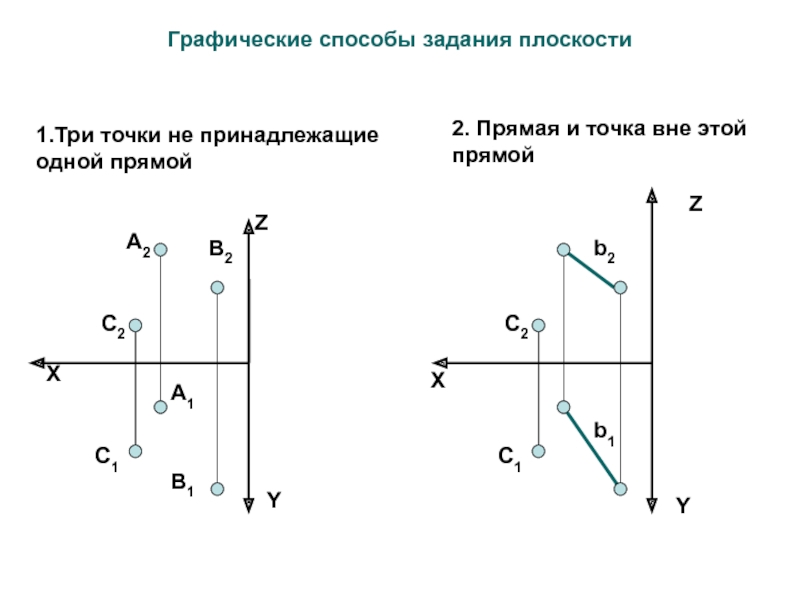
Слайд 5 Графические способы задания плоскости
X
Z
Y
А2
А1
В1
C2
C1
В2
X
Y
b1
C2
C1
b2
1.Три точки не принадлежащие одной прямой
2. Прямая и точка вне
этой прямойZ
Слайд 8Y
Z
X
aп1
aП3
aП2
ax
ay
az
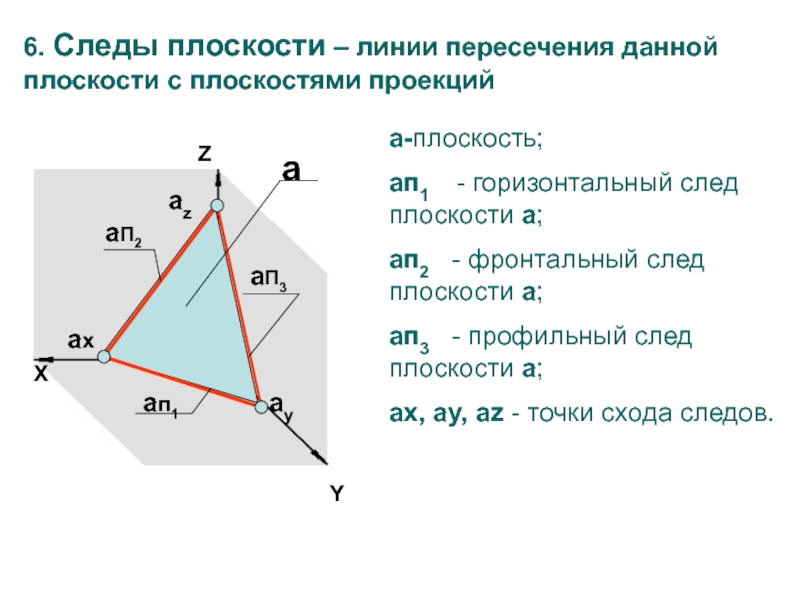
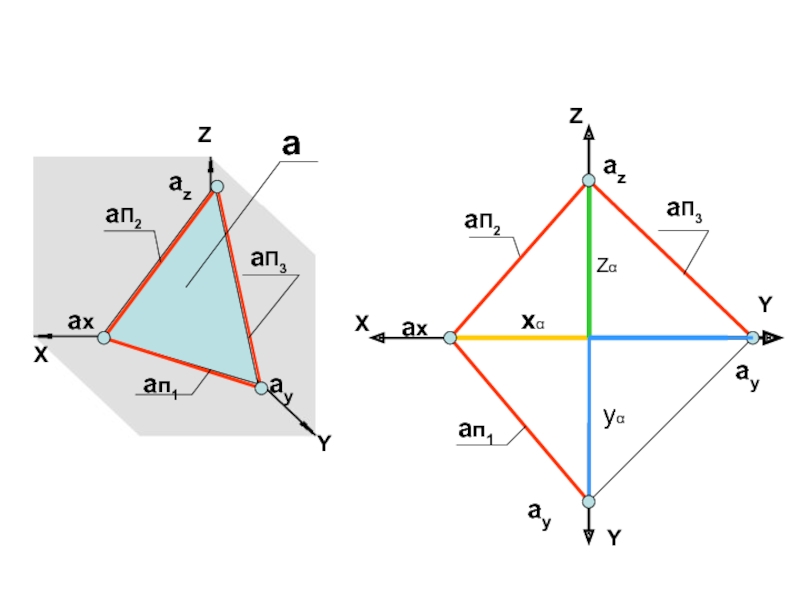
6. Следы плоскости – линии пересечения данной плоскости с плоскостями
проекций
a
a-плоскость;
aп1 - горизонтальный след плоскости a;
aп2 -
фронтальный след плоскости a;aп3 - профильный след плоскости a;
ax, ay, az - точки схода следов.
Слайд 10ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
1. Относительно плоскостей проекций плоскости разделяют:
• плоскости частного положения
• плоскости общего положения
2. Плоскости частного положения разделяют:
плоскости параллельные плоскостям проекций – плоскости уровня
плоскости перпендикулярные плоскостям проекций – плоскости проецирующие
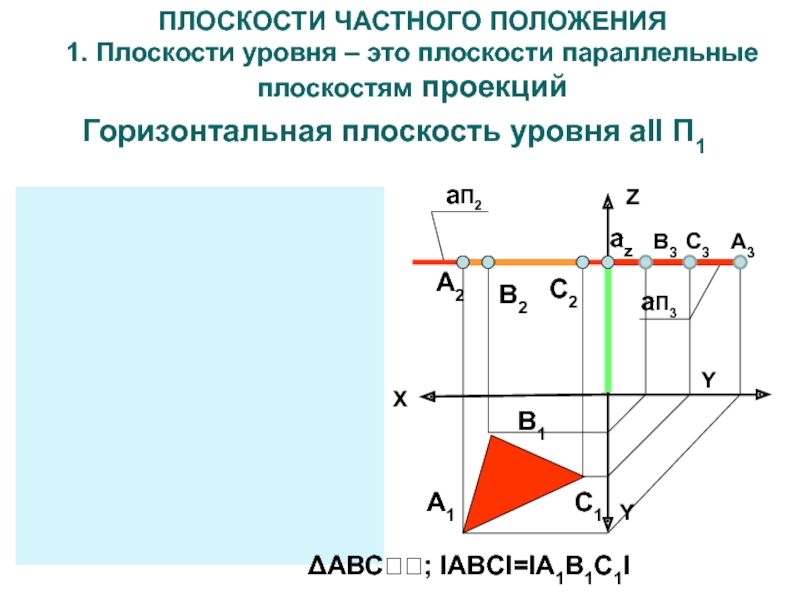
Слайд 11ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ 1. Плоскости уровня – это плоскости параллельные плоскостям
проекций
Горизонтальная плоскость уровня aII П1
Z
X
Y
Y
aП2
aП3
az
Y
Z
X
aП3
aП2
az
a
А1
В1
С1
А2
В2
С2
А1
С1
В1
А2
В2
С2
ΔАВС; IABCI=IA1B1C1I
В3 С3 А3
Слайд 12Z
X
Y
Y
bп1
bП3
by
Y
Z
X
bп1
bП3
by
by
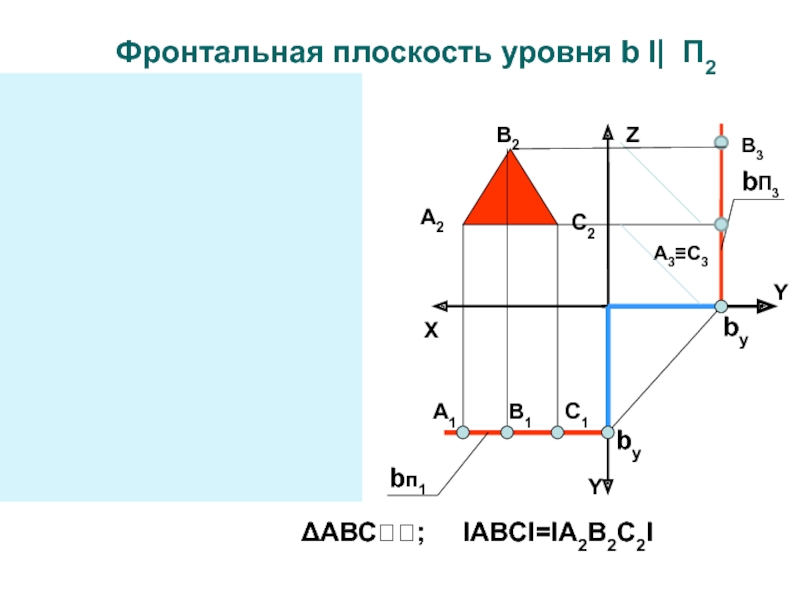
Фронтальная плоскость уровня b I| П2
А1
В1
С1
С2
В2
А2
b
ΔАВС; IABCI=IA2B2C2I
А3≡С3
В3
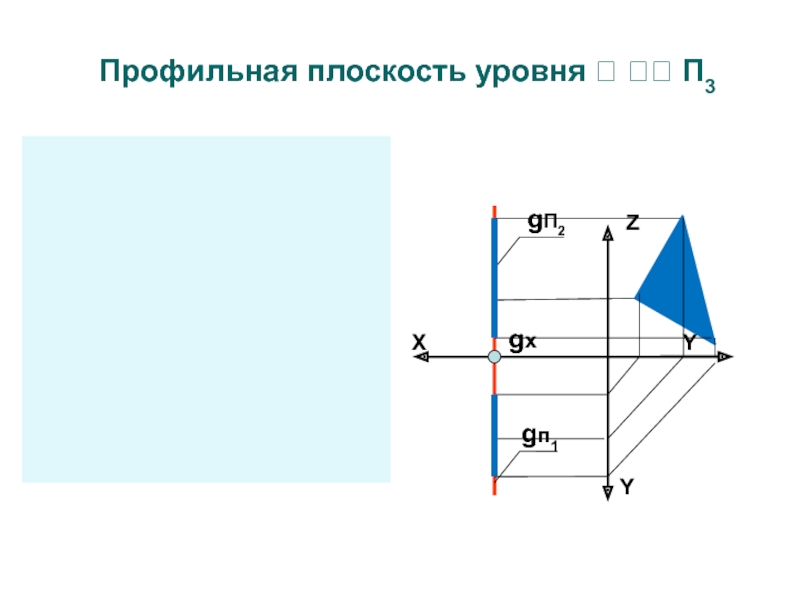
Слайд 14Особенности чертежа плоскостей уровня
Фигуры принадлежащие плоскостям уровня проецируются в натуральную
величину на параллельную плоскость проекций
На другие плоскости проекций фигуры принадлежащие
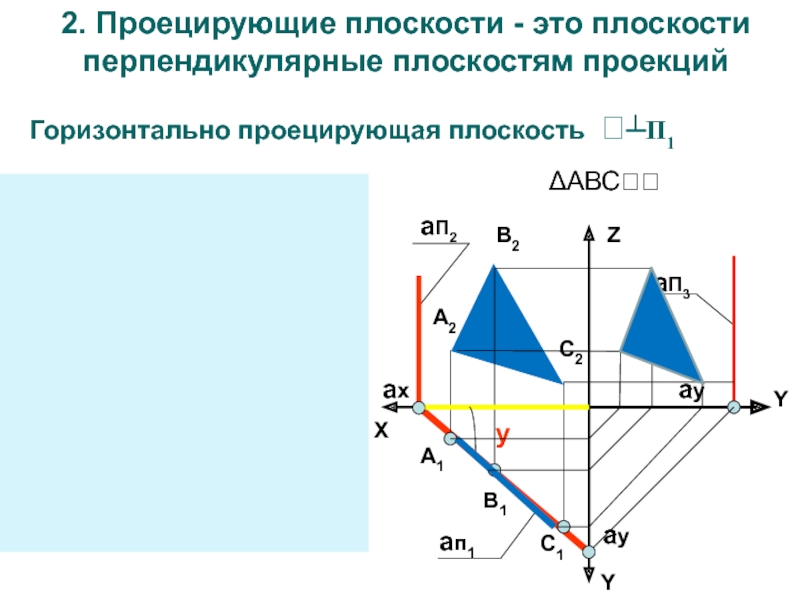
плоскостям уровня проецируются в прямую линиюСлайд 152. Проецирующие плоскости - это плоскости перпендикулярные плоскостям проекций
Горизонтально проецирующая
плоскость ┴П1
X
Y
Y
aП2
aП3
Z
X
aп1
aП2
ax
ax
Z
aп1
aП3
a
Y
ay
y
ay
ay
А1
В1
С1
А2
В2
С2
ΔАВС
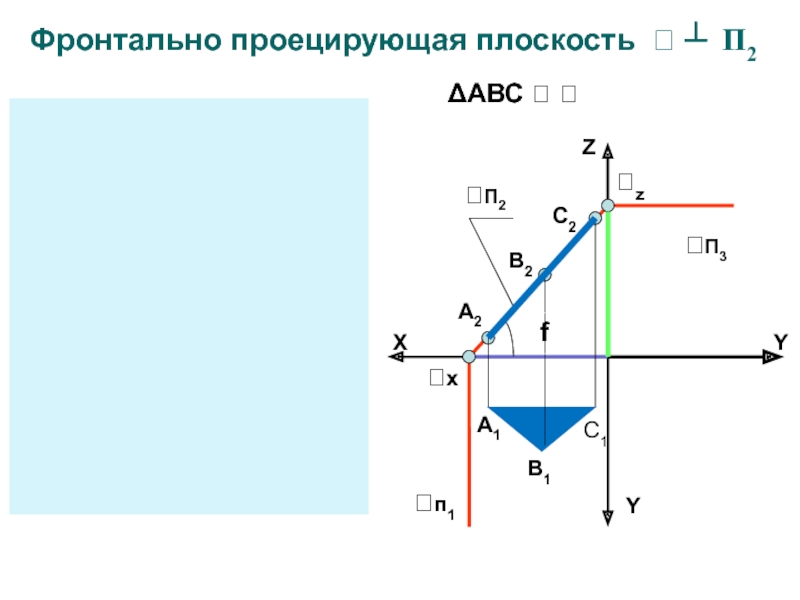
Слайд 16Фронтально проецирующая плоскость ┴ П2
Z
X
Y
Y
П2
п1
x
Y
Z
X
П2
z
П3
П1
П3
z
x
А2
В2
С2
А1
В1
С1
f
ΔАВС
Слайд 18Фигуры принадлежащие проецирующим плоскостям на перпендикулярную плоскость проекций проецируются в
прямую линию (вырожденная проекция)
Угол наклона между вырожденной проекцией и осями
координат равен углу между заданной плоскостью и плоскостью проекцийОсобенности чертежа проецирующих плоскостей
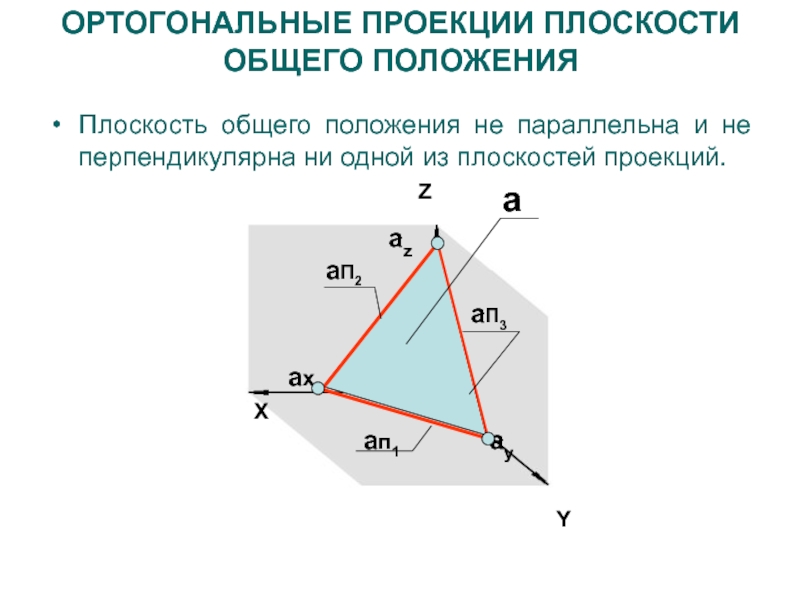
Слайд 19ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
Плоскость общего положения не параллельна и
не перпендикулярна ни одной из плоскостей проекций.
Y
Z
X
aп1
aП3
aП2
ax
ay
az
a
Слайд 20ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ
ПЛОСКОСТИ
Точка принадлежит плоскости, если она принадлежит
прямой в этой плоскости
Прямая принадлежит плоскости если она проходит:
а) через
две точки этой плоскостиб) через точку плоскости параллельно какой-либо прямой этой плоскости
Слайд 22ОСОБЫЕ ЛИНИИ ПЛОСКОСТИ
ЛИНИИ УРОВНЯ ПЛОСКОСТИ – линии параллельные плоскостям проекций
и принадлежащие данной плоскости;
ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА (ЛНН) ПЛОСКОСТИ – определяют
угол наклона данной плоскости к одной из плоскостей проекций. ЛНН перпендикулярны линиям уровня:
горизонтали на плоскости П1;
фронтали на плоскости П2.
Слайд 23Z
X
aп1
aП3
aП2
ax
ay
az
a
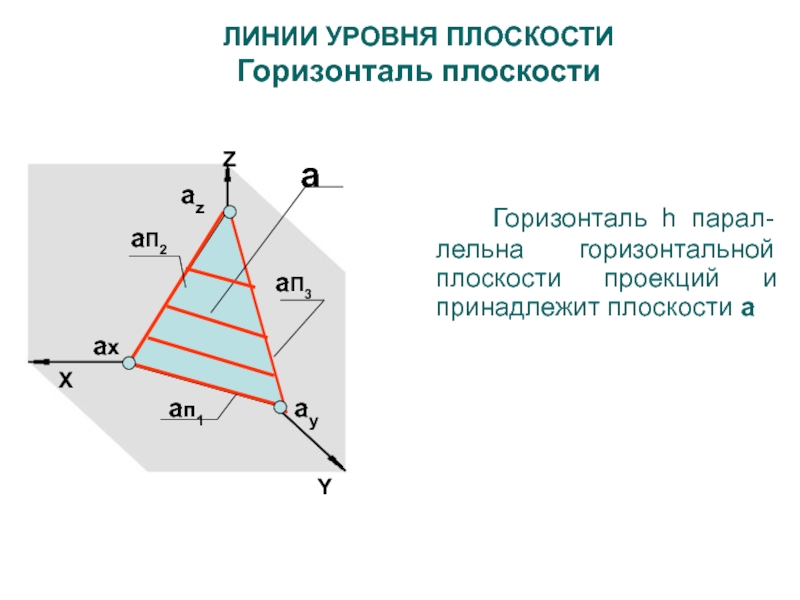
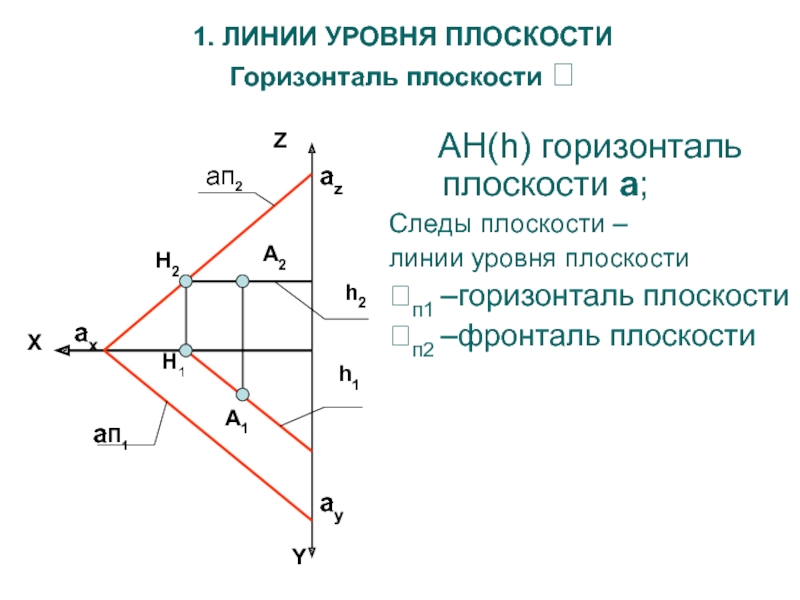
ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Горизонталь плоскости
Y
Горизонталь h парал-лельна горизонтальной
плоскости проекций и принадлежит плоскости a
Слайд 24 AН(h) горизонталь плоскости a;
Следы плоскости –
линии уровня плоскости
п1 –горизонталь плоскости
п2 –фронталь плоскости
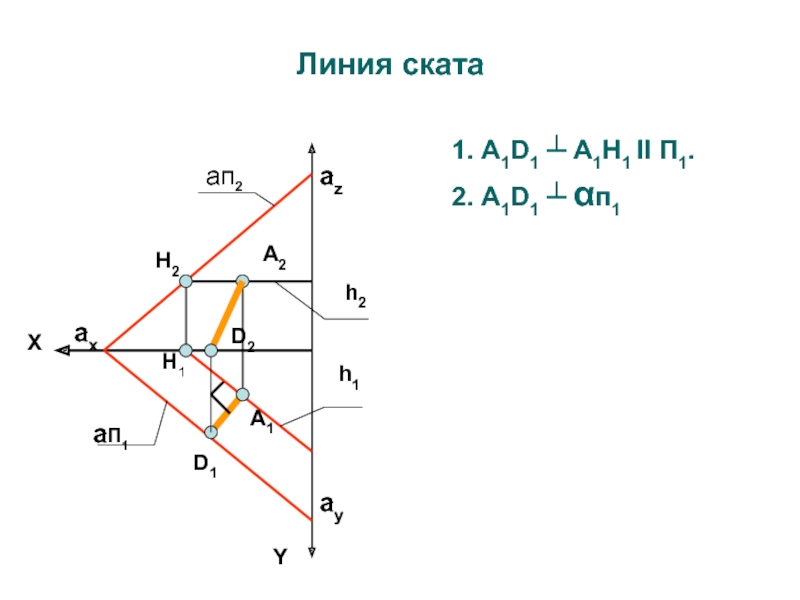
1. ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Горизонталь
плоскости aп2
aП1
Y
Z
X
ax
А2
А1
h2
h1
Н2
Н1
ay
az
Слайд 28Z
X
aп1
aП3
aП2
ax
ay
az
a
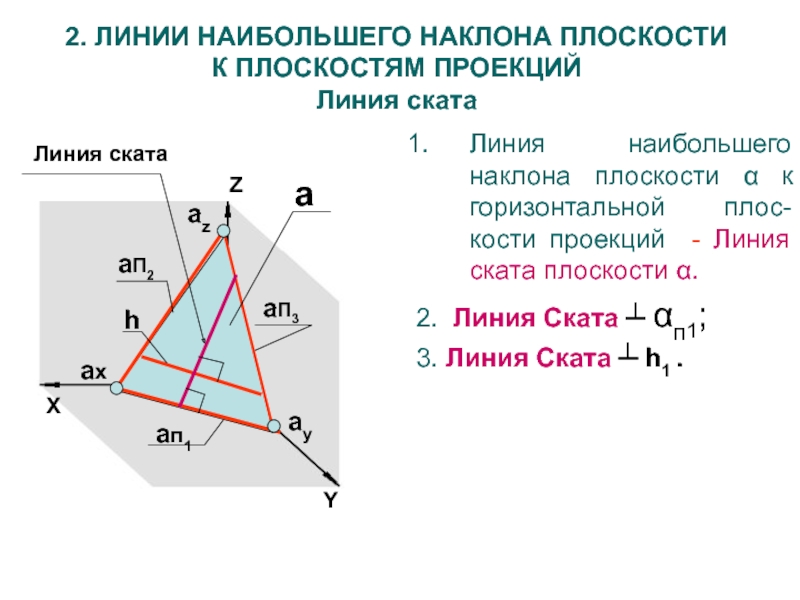
2. ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
К ПЛОСКОСТЯМ ПРОЕКЦИЙ
Линия ската
Линия наибольшего наклона
плоскости α к горизонтальной плос-кости проекций - Линия ската плоскости
α.2. Линия Ската ┴ αп1;
3. Линия Ската ┴ h1 .
h
Y
Линия ската
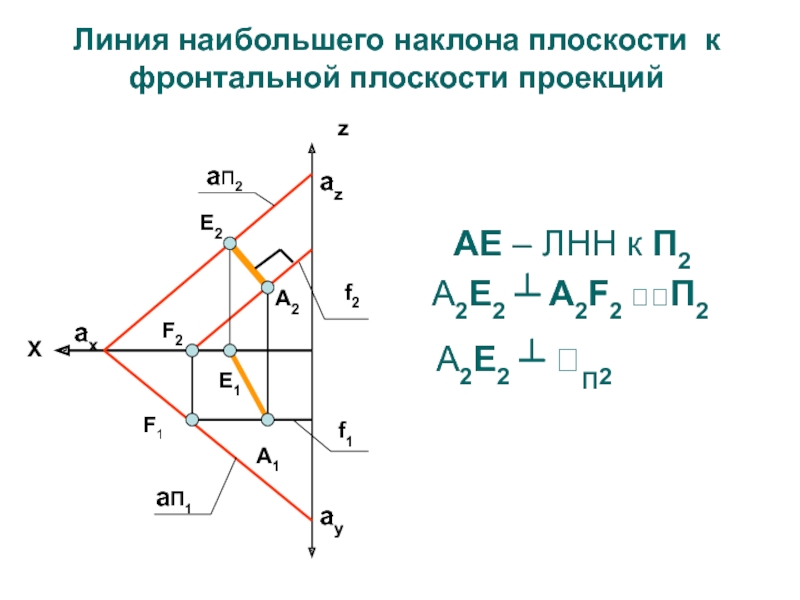
Слайд 32 АЕ – ЛНН к П2
A2Е2 ┴ A2F2
П2
A2Е2 ┴ п2
aп2
aП1
z
ax
А2
A1
f2
f1
F2
F1
X
az
ay
Е1
Е2
Линия наибольшего наклона плоскости к фронтальной
плоскости проекцийСлайд 33А2
F2
В2
А1
F1
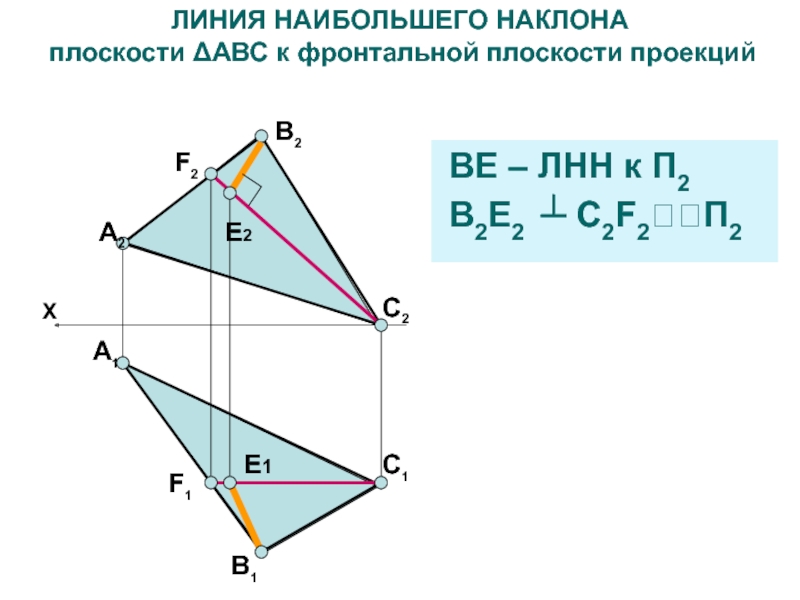
ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости ΔАВС к фронтальной плоскости проекций
BE
– ЛНН к П2
В2E2 ┴ C2F2П2
X
Е2
Е1
В1
С1
С2
Слайд 34
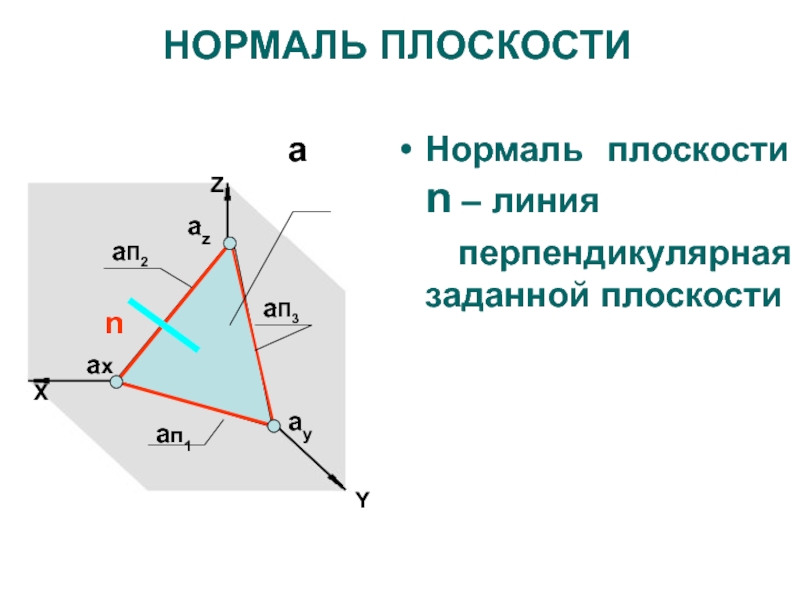
НОРМАЛЬ ПЛОСКОСТИ
Нормаль плоскости n – линия
перпендикулярная
заданной плоскости
Z
X
aп1
aП3
aП2
ax
ay
az
Y
a
n
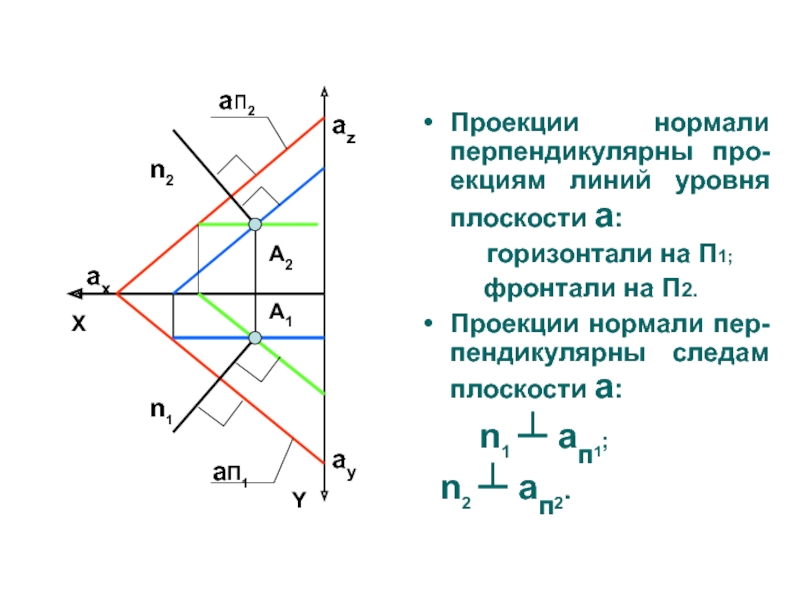
Слайд 35Проекции нормали перпендикулярны про-екциям линий уровня плоскости a:
горизонтали на П1;
фронтали на П2.Проекции нормали пер-пендикулярны следам плоскости a:
n1 ┴ aп1;
n2 ┴ aп2.
aП1
Y
ax
А2
А1
n2
n1
X
az
ay
aп2
Слайд 36А2
В2
А1
X
В1
С1
С2
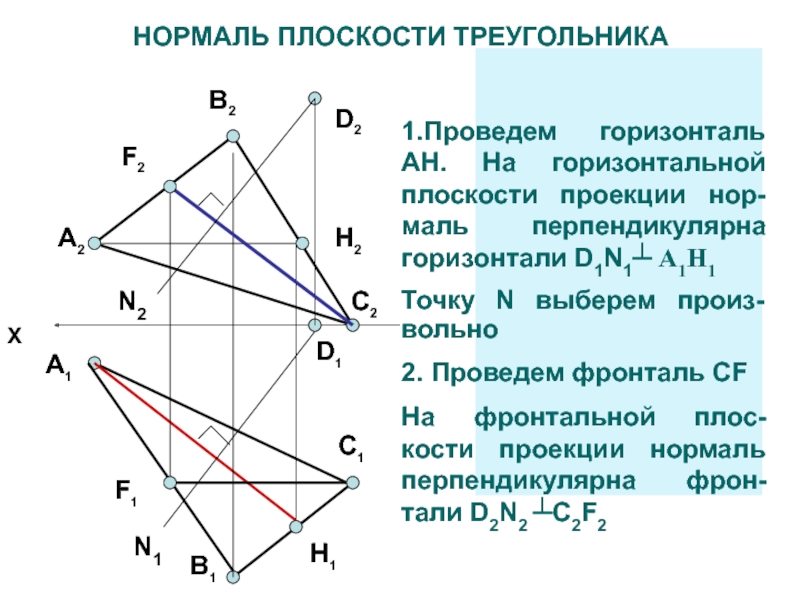
Через точку D провести перпендикуляр к плоскости треугольника АВС
А(80,20,30)
В(40,60,60)
С(0,40,0)
D(10,0,70)
D2
D1
1.Проведем горизонталь
AH. На горизонтальной плоскости проекции нор-маль перпендикулярна горизонтали D1N1┴ А1Н1
Точку
N выберем произ-вольно 2. Проведем фронталь CF
На фронтальной плос-кости проекции нормаль перпендикулярна фрон-тали D2N2 ┴C2F2
H1
H2
F1
F2
НОРМАЛЬ ПЛОСКОСТИ ТРЕУГОЛЬНИКА
N1
N2
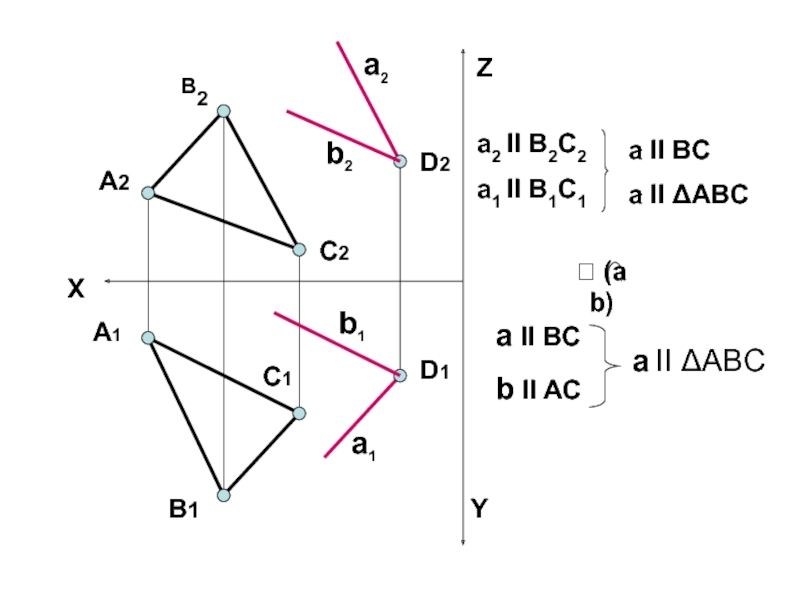
Слайд 39ПРЯМАЯ ПАРАЛЛЕЛЬНА ПЛОСКОСТИ, ЕСЛИ ОНА ПАРАЛЛЕЛЬНА ЛЮБОЙ ПРЯМОЙ ПРИНАДЛЕЖАЩЕЙ ПЛОСКОСТИ
2.
ПЛОСКОСТИ ПАРАЛЛЕЛЬНЫ, ЕСЛИ ДВЕ ПЕРЕ-СЕКАЮЩИЕСЯ ПРЯМЫЕ ОДНОЙ ПЛОСКОСТИ, ПАРАЛЛЕЛЬНЫ ДВУМ
ПЕРЕСЕКАЮЩИМСЯ ПРЯ-МЫМ ДРУГОЙ ПЛОСКОСТИ
Слайд 41X
Y
Z
A2
B2
A1
C2
C1
B1
a1
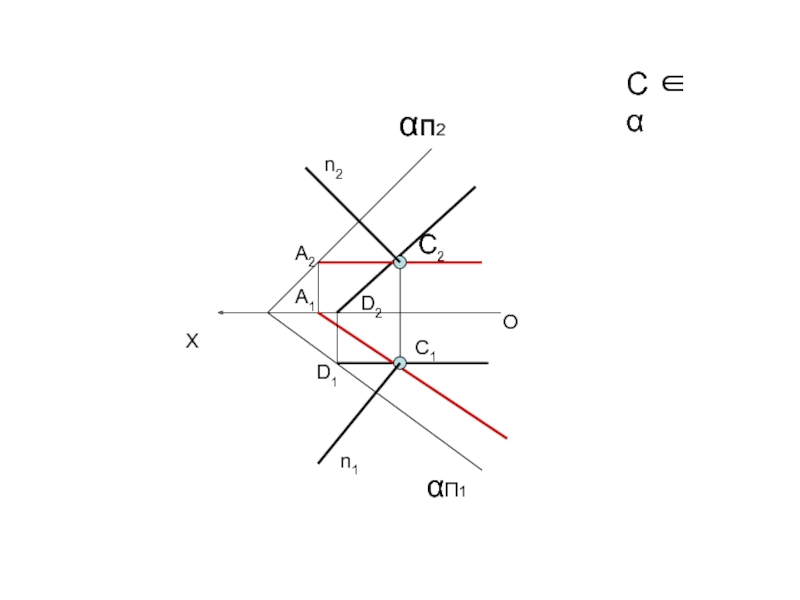
a2
D2
D1
a2 II B2C2
a1 II B1C1
a II BC
a II ΔABC
b1
b2
(a
b)
a II BC
b II AC
a II ΔABC
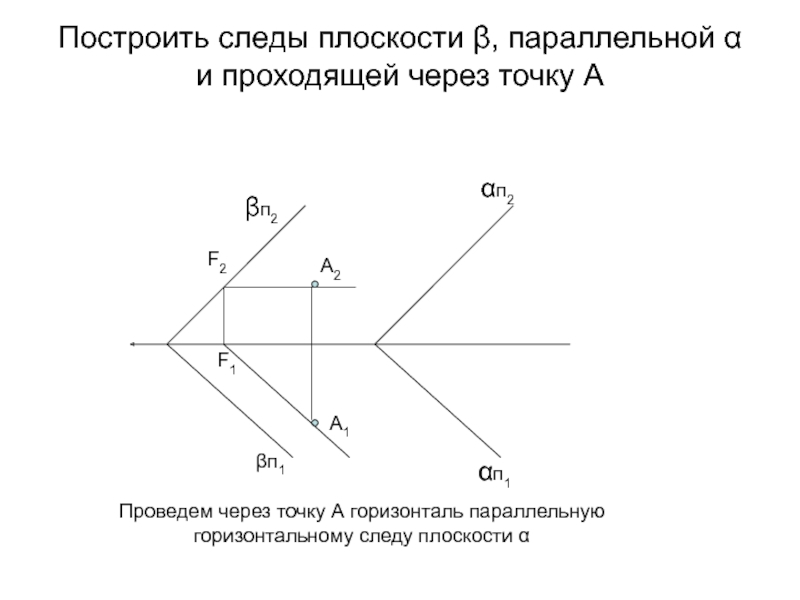
Слайд 42Построить следы плоскости β, параллельной α и проходящей через точку
А
αп2
αп1
А2
А1
Проведем через точку А горизонталь параллельную горизонтальному следу плоскости α
F1
F2
βп2
βп1
Слайд 43ПРЯМАЯ ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ,
ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ
ПРЯМАЯ ПЕРПЕНДИКУЛЯРНА ПЛОСКОСТИ, ЕСЛИ ОНА ПЕРПЕНДИКУЛЯРНА
ДВУМ ПЕРЕСЕКАЮЩИМСЯ ПРЯМЫМ ПРИНАДЛЕЖАЩИМ ЭТОЙ ПЛОСКОСТИ
В соответствии с теоремой о
проекциях прямого угла прямая перпендикулярна плоскости, если она перпендикулярна одноименным проекциям горизонтали и фронтали плоскости· ДВЕ ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫ, ЕСЛИ ОДНА ПЛОСКОСТЬ ПРОХОДИТ ЧЕРЕЗ ПЕРПЕНДИКУЛЯР К ДРУГОЙ
Слайд 46Через точку D провести перпендикуляр к плоскости Δ АВС и
плоскость α (n∩a) перпендикулярную Δ АВС
А(80,10,30)
В(40,60,50)
С(10,45,0)
D(50,55,5)
Слайд 48ПЕРЕСЕКАЮЩИЕСЯ ПРЯМАЯ И ПЛОСКОСТЬ
ПРЯМАЯ И ПЛОСКОСТЬ ПЕРЕСЕКАЮТСЯ, ЕСЛИ
У НИХ ЕСТЬ ОДНА ОБЩАЯ ТОЧКА
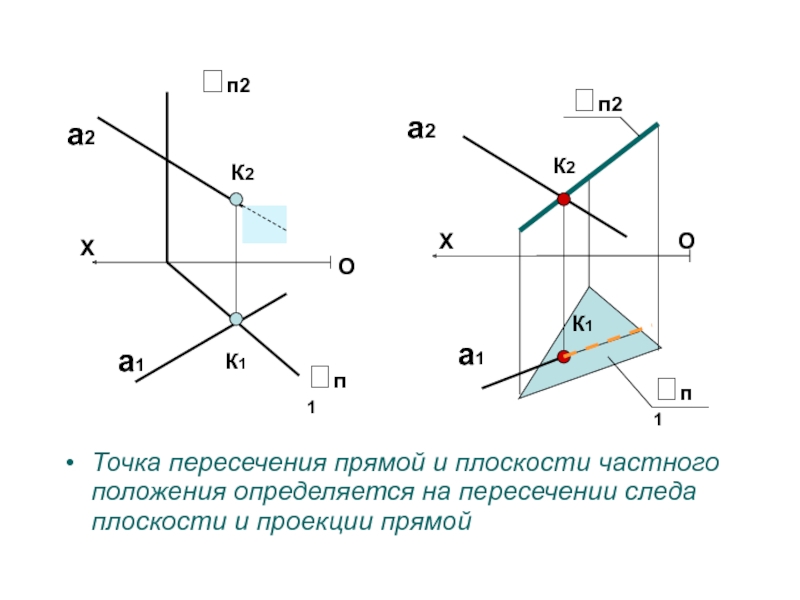
Слайд 49Точка пересечения прямой и плоскости частного положения определяется на пересечении
следа плоскости и проекции прямой
X
O
a1
а2
п1
п2
К1
К2
X
O
a1
а2
п1
п2
К1
К2
Слайд 51Пересечение прямой общего положения и плоскости общего положения
СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ
ПЛОСКОСТЕЙ
1. Через прямую проводят плоскость частного положения α ┴ П1.
2.
Определяют линию пересечения заданной плоскости и введенной плоскости α.3. Определяют точку пересечения заданной прямой и построенной линии пересечения.
Это искомая точка пересечения заданной плоскости и прямой а.
4. Определяют видимость заданной прямой.
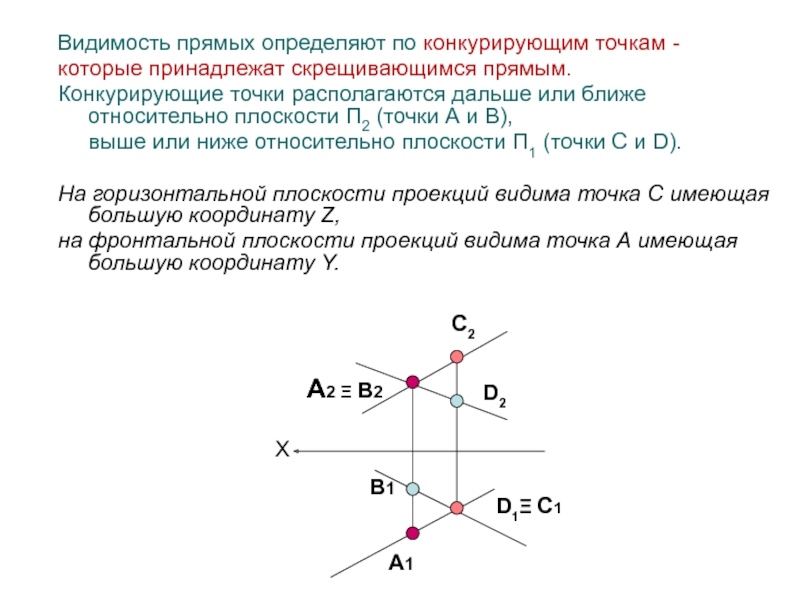
Слайд 53Видимость прямых определяют по конкурирующим точкам -
которые принадлежат скрещивающимся прямым.
Конкурирующие точки располагаются дальше или ближе относительно плоскости П2 (точки
А и В), выше или ниже относительно плоскости П1 (точки C и D).
На горизонтальной плоскости проекций видима точка С имеющая большую координату Z,
на фронтальной плоскости проекций видима точка А имеющая большую координату Y.
А1
С2
D2
D1Ξ C1
В1
А2 Ξ В2
X
Слайд 561. ПЛОСКОСТИ ПЕРЕСЕКАЮТСЯ, ЕСЛИ У НИХ ЕСТЬ ДВЕ ОБЩИЕ ТОЧКИ
2.
ПЛОСКОСТИ ПЕРЕСЕКАЮТСЯ ПО ПРЯМОЙ ЛИНИИ, КОТОРАЯ ПРОХОДИТ ЧЕРЕЗ ДВЕ ОБЩИЕ
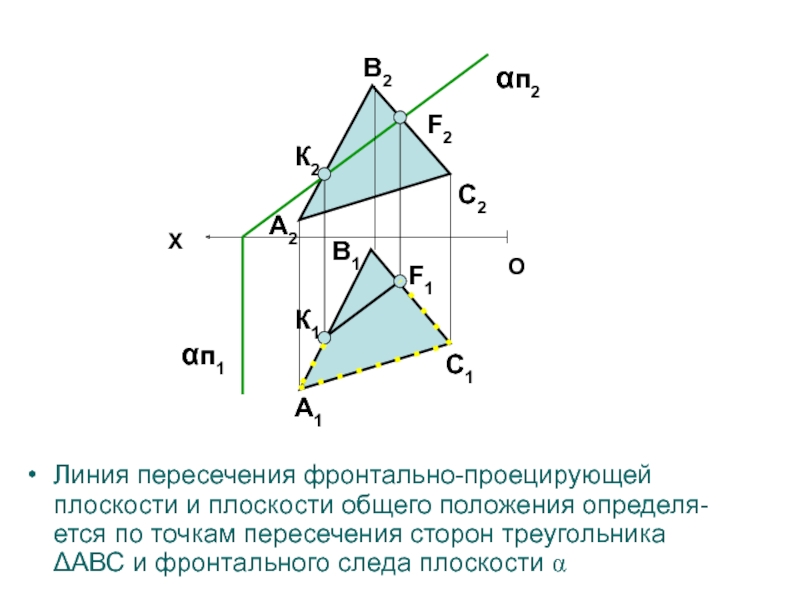
ТОЧКИ ПЛОСКОСТЕЙСлайд 57Линия пересечения фронтально-проецирующей плоскости и плоскости общего положения определя-ется по
точкам пересечения сторон треугольника ΔАВС и фронтального следа плоскости α
X
O
К2
F2
F1
К1
A2
B2
C2
B1
A1
C1
αп1
αп2
Слайд 58Для построения линии пересечения плоскостей достаточно определить две общие точки
заданных плоскостей
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
ОБЩЕГО ПОЛОЖЕНИЯ
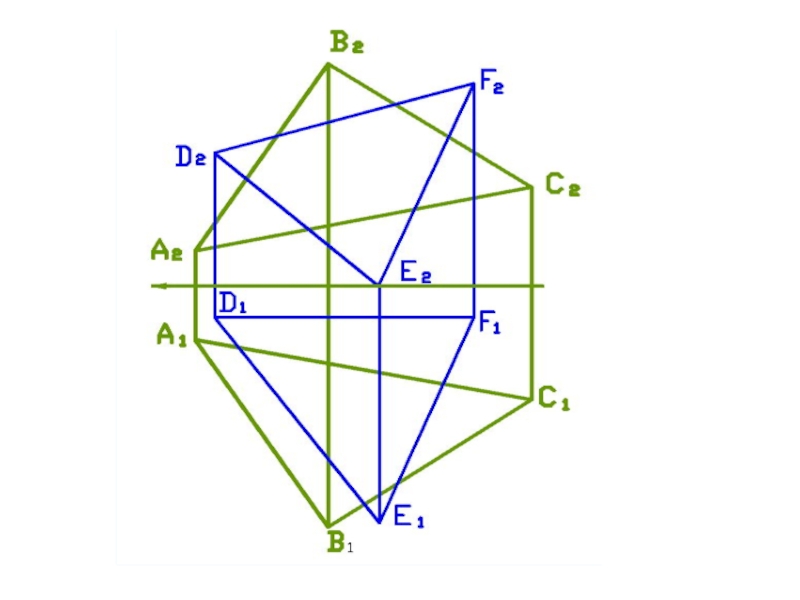
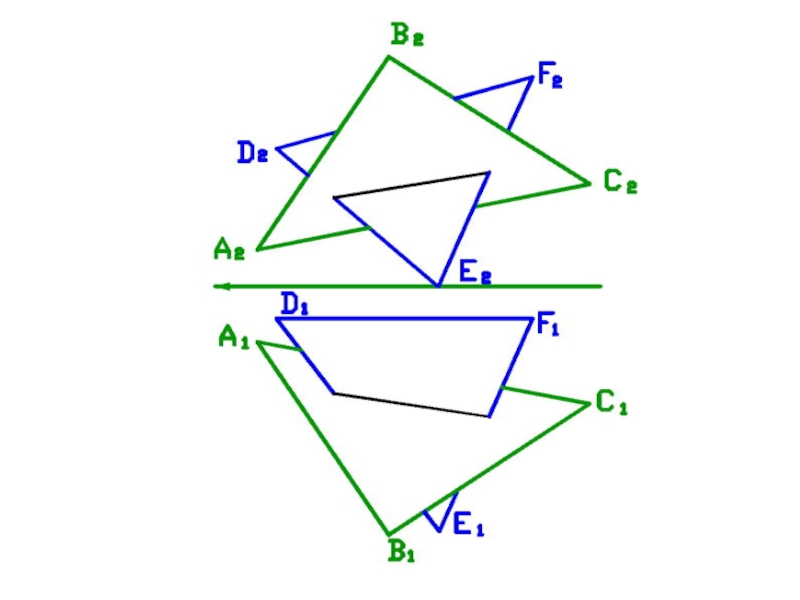
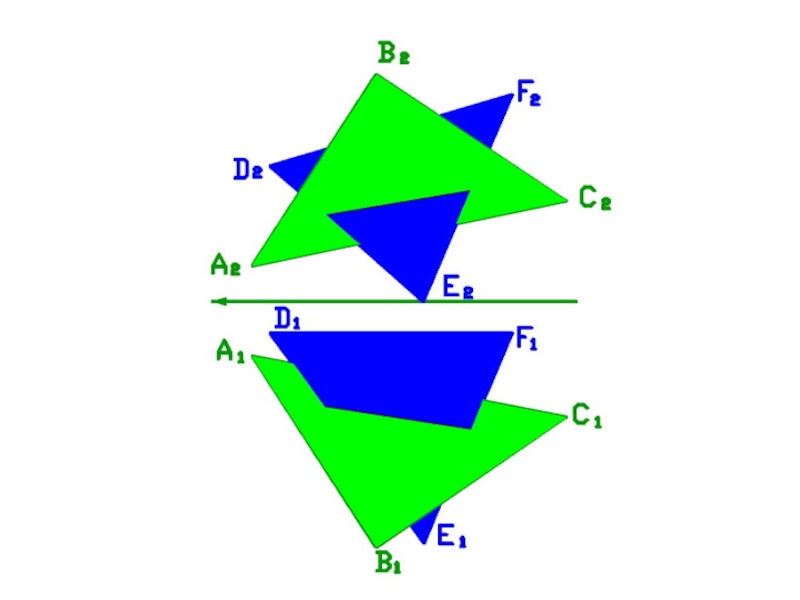
Слайд 59Задача
Построить линию пересечения треугольников ΔABC и ΔDEF.
A(100,
20, 20), B(65, 70, 70), C(10, 30,25),
D(90, 10,
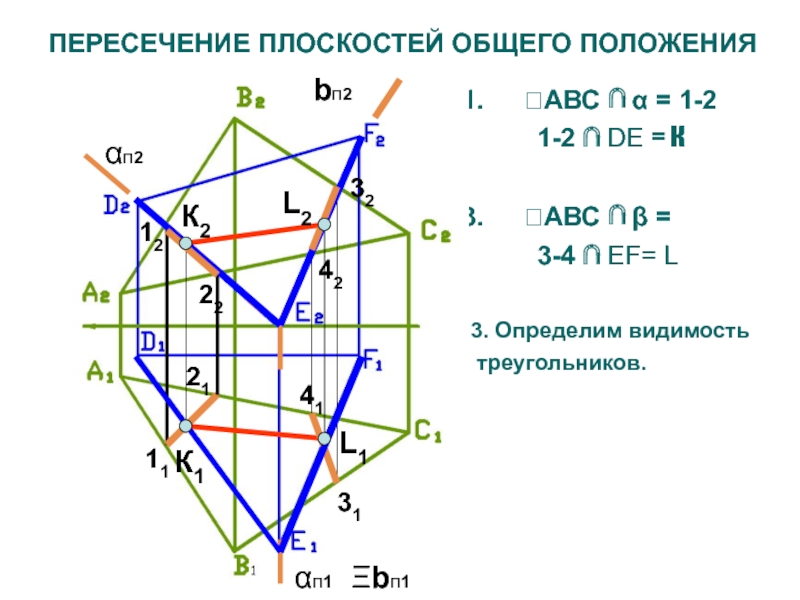
55), E(45, 70, 0), F(20, 10, 65)Слайд 62ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ
АВС ∩ α = 1-2
1-2 ∩ DE = К
АВС ∩ β =
3-4 ∩ EF= L3. Определим видимость
треугольников.
αп2
αп1
К1
К2
bп2
Ξbп1
L2
L1
12
22
11
21
32
42
31
41
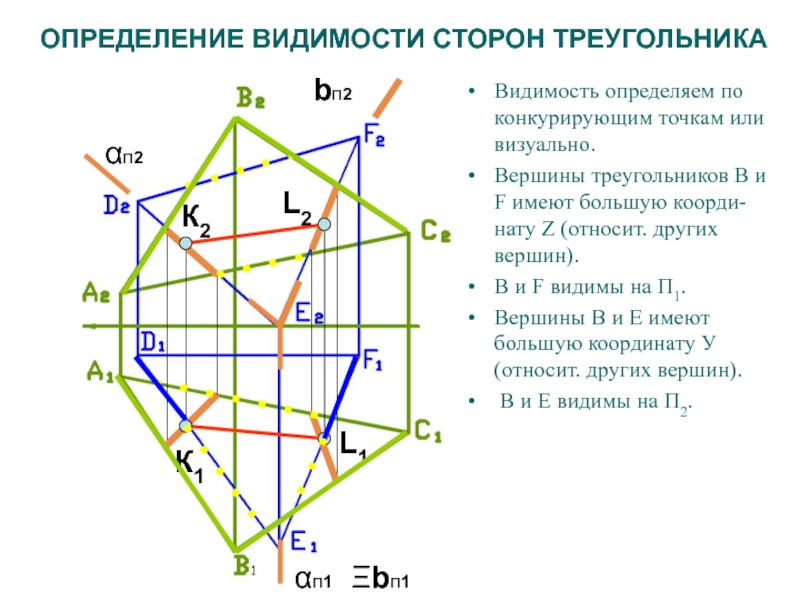
Слайд 63ОПРЕДЕЛЕНИЕ ВИДИМОСТИ СТОРОН ТРЕУГОЛЬНИКА
Видимость определяем по конкурирующим точкам или визуально.
Вершины
треугольников В и F имеют большую коорди-нату Z (относит. других
вершин).В и F видимы на П1.
Вершины В и Е имеют большую координату У (относит. других вершин).
В и Е видимы на П2.
αп2
αп1
К1
К2
bп2
Ξbп1
L2
L1