Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 3 Способ прямоугольного треугольника. Плоскости
Содержание
- 1. Лекция 3 Способ прямоугольного треугольника. Плоскости
- 2. Способы задания прямой1. По координатам точек концов
- 3. Способ прямоугольного треугольникаНатуральная величина отрезка прямой общего
- 4. Способ прямоугольного треугольника
- 5. Способ прямоугольного треугольника. Прямая задачаДано: А₁В₁ и
- 6. Вопрос 1Дано: А1В1 иА2В2 – проекции прямой
- 7. Способ прямоугольного треугольника. Обратная задачаДано: НВАВ, =30⁰,=45⁰А(40,50,5)ХАYBZA
- 8. Вопрос 2Завершить фразу:Диаметр круговой диаграммы равен ... .
- 9. Следы плоскости – линии пересечения заданной плоскости
- 10. Следы плоскостиДля построения следов плоскости достаточно определить следы двух прямых этой плоскости
- 11. Плоскости общего положения Плоскости общего положения -
- 12. Плоскости частного положения Плоскости параллельные плоскостям проекцийПлоскости перпендикулярные плоскостям проекций
- 13. Плоскости параллельные плоскостям проекцийПлоскость (АВС) параллельна горизонтальной плоскости проекций 1Проекция А1В1С1 равна его натуральной величине
- 14. Плоскости параллельные плоскостям проекцийПлоскость АВС параллельна 1 - горизонтальная плоскость
- 15. Плоскости параллельные плоскостям проекцийПлоскость АВС параллельна 2 - фронтальная плоскость
- 16. Плоскости параллельные плоскостям проекцийПлоскость АВС параллельна 3 - профильная плоскость проекций
- 17. Плоскости перпендикулярные плоскостям проекцийПлоскость (АВС) перпендикулярна горизонтальной плоскости проекций 1 Плоскость - горизонтально-проецирующая плоскость
- 18. Плоскости перпендикулярные плоскостям проекцийПлоскость АВС перпендикулярна 1 - горизонтально-проецирующая плоскость
- 19. Плоскости перпендикулярные плоскостям проекцийПлоскость АВС перпендикулярна 2 - фронтально-проецирующая плоскость
- 20. Плоскости перпендикулярные плоскостям проекцийПлоскость АВС перпендикулярна 3 - профильно-проецирующая плоскость
- 21. Вопрос 3Вырожденную проекцию имеют плоскости:УровняПроецирующиеОбщего положенияВсе
- 22. Особые линии плоскости. Горизонталь плоскостиГоризонталь плоскости
- 23. Особые линии плоскости. Фронталь плоскостиФронталь плоскости
- 24. Особые линии плоскости. Горизонталь плоскостиAD принадлежит плоскости АВСAD параллельна 1AD - горизонталь АВС
- 25. Особые линии плоскости. Фронталь плоскостиCD принадлежит АВСCD параллельна 2CD - фронталь АВС
- 26. Особые линии плоскостиm - горизонталь плоскости n - фронталь плоскости
- 27. Вопрос 4Построение проекций горизонтали плоскости следует начинать с плоскостиП1П2П3Оси х
- 28. Особые линии плоскости. Линии наибольшего наклона
- 29. Особые линии плоскости. Линии наибольшего наклона
- 30. Особые линии плоскости. Линия скатаMN принадлежит MN
- 31. Линия наибольшего наклона плоскостиAD - фронталь АВСВЕ
- 32. Вопрос 5Построение линии ската плоскости следует начинать с ГоризонталиФронталиСледовПрофильной проекции
- 33. ВЫВОДЫОсобые линии плоскости позволяют решать позиционные задачи
- 34. Плоскость. Позиционные и метрические задачиПрямая может
- 35. Особые линии плоскости. НормальНормаль - прямая перпендикулярная
- 36. НормальAD - фронталь АВСЕС - горизонталь АВСn
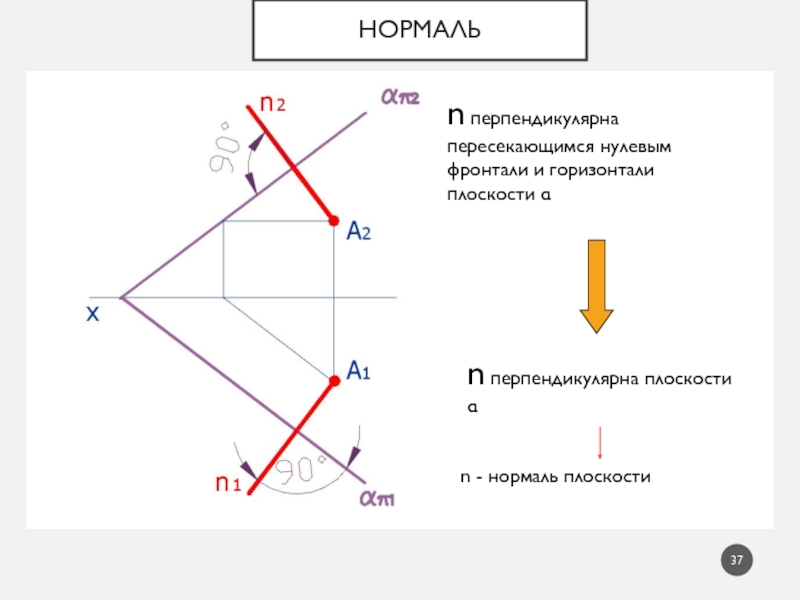
- 37. Нормальn перпендикулярна пересекающимся нулевым фронтали и горизонтали
- 38. Построение проекций плоской фигуры по особым линиям
- 39. Построение проекций плоской фигуры по особым линиям
- 40. Построение проекций плоской фигуры по особым линиям
- 41. ВЫВОДЫОсобые линии плоскости позволяют решать позиционные задачи
- 42. Скачать презентанцию
Способы задания прямой1. По координатам точек концов отрезка прямой (проекциям отрезка прямой) - А(x,y,z) и В (x,y,z) 2. Параметрами отрезка прямой линии: - натуральной величиной отрезка (НВ) - углами наклона к
Слайды и текст этой презентации
Слайд 1
Лекция 3
Способ прямоугольного треугольника.
Плоскости
Способ прямоугольного треугольника
Задание плоскости
Следы плоскости
Плоскости общего и
частного положения
Слайд 2Способы задания прямой
1. По координатам точек концов отрезка прямой (проекциям
отрезка прямой) - А(x,y,z) и В (x,y,z)
2. Параметрами отрезка
прямой линии:- натуральной величиной отрезка (НВ)
- углами наклона к плоскостям проекций - (П₁) и ψ (П₂):
- угол между линией отрезка и горизонтальной плоскостью (П₁)
ψ- угол между линией отрезка и фронтальной плоскостью (П₂)
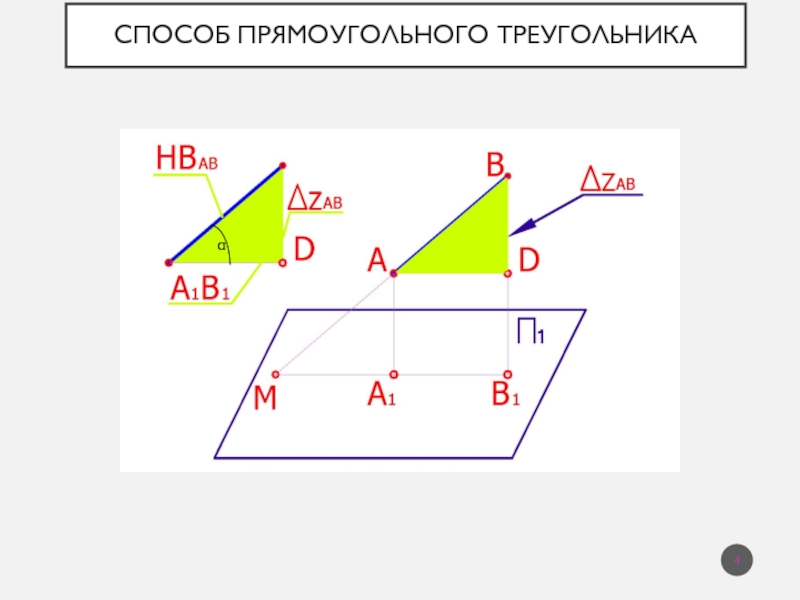
Слайд 3Способ прямоугольного треугольника
Натуральная величина отрезка прямой общего положения равна гипотенузе
прямоугольного треугольника,
одним катетом которого является проекция отрезка на любую
плоскость проекций, другим – разность расстояний концов отрезка до той же плоскости проекций
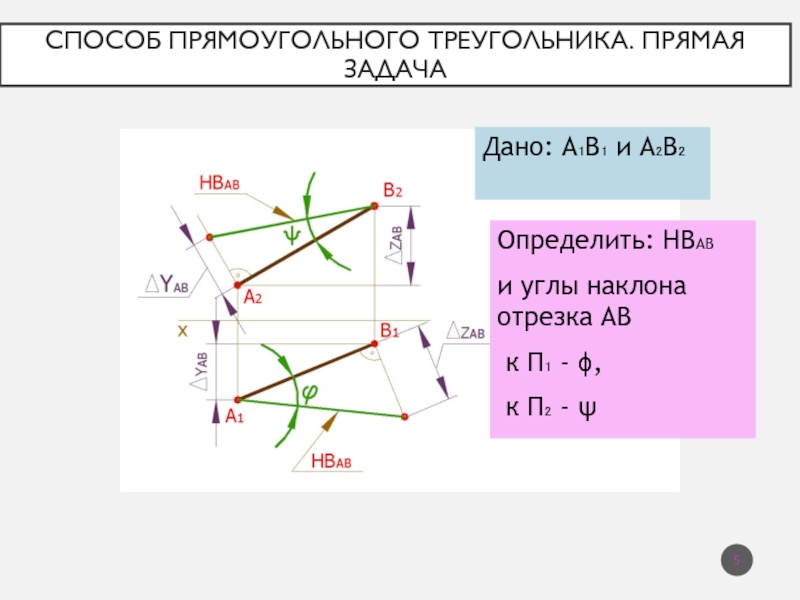
Слайд 5Способ прямоугольного треугольника. Прямая задача
Дано: А₁В₁ и А₂В₂
Определить: НВАВ
и
углы наклона отрезка АВ
к П₁ - ,
к П₂
- Слайд 6Вопрос 1
Дано:
А1В1 иА2В2 – проекции прямой общего положения
Дополнить фразу:
Для
определения ψ и ϕ нужно ... .
Слайд 9Следы плоскости – линии пересечения заданной плоскости с плоскостями проекций
2
- фронтальный след плоскости
1 - горизонтальный след плоскости
3
- профильный след плоскости x, y и z - точки схода плоскости
Слайд 10Следы плоскости
Для построения следов плоскости достаточно определить следы двух прямых
этой плоскости
Слайд 11Плоскости общего положения
Плоскости общего положения - это плоскости, неперпендикулярные
и непараллельные плоскостям проекций
Плоскости общего положения не проецируются в натуральную
величинуСлайд 12Плоскости частного положения
Плоскости параллельные плоскостям проекций
Плоскости перпендикулярные плоскостям проекций
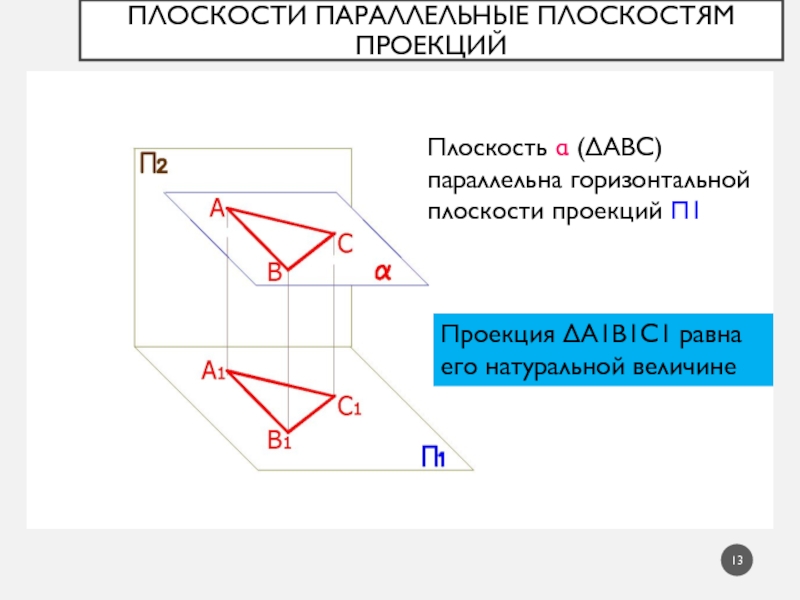
Слайд 13Плоскости параллельные плоскостям проекций
Плоскость (АВС) параллельна горизонтальной плоскости проекций
1
Проекция А1В1С1 равна его натуральной величине
Слайд 14Плоскости параллельные плоскостям проекций
Плоскость АВС параллельна 1 - горизонтальная плоскость
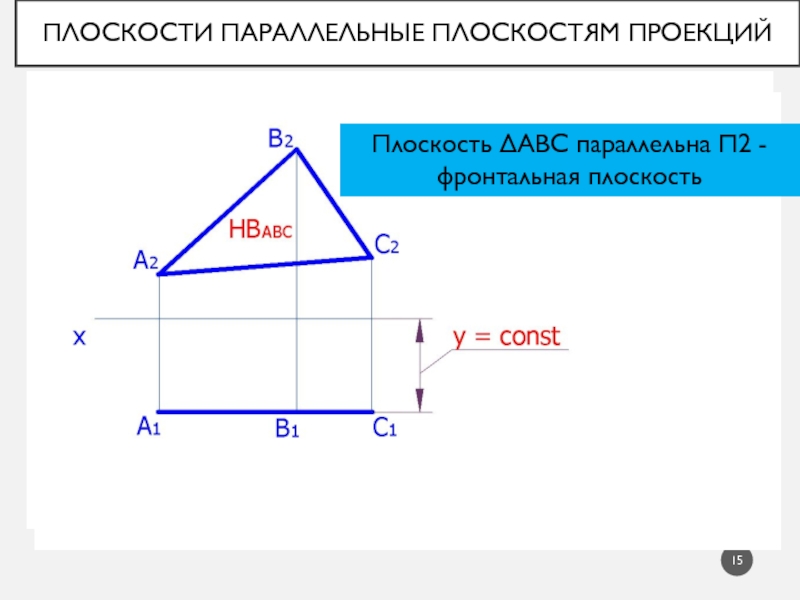
Слайд 15Плоскости параллельные плоскостям проекций
Плоскость АВС параллельна 2 - фронтальная плоскость
Слайд 16Плоскости параллельные плоскостям проекций
Плоскость АВС параллельна 3 - профильная плоскость
проекций
Слайд 17Плоскости перпендикулярные плоскостям проекций
Плоскость (АВС) перпендикулярна горизонтальной плоскости проекций
1
Плоскость - горизонтально-проецирующая плоскость
Слайд 18Плоскости перпендикулярные плоскостям проекций
Плоскость АВС перпендикулярна 1 - горизонтально-проецирующая плоскость
Слайд 19Плоскости перпендикулярные плоскостям проекций
Плоскость АВС перпендикулярна 2 - фронтально-проецирующая плоскость
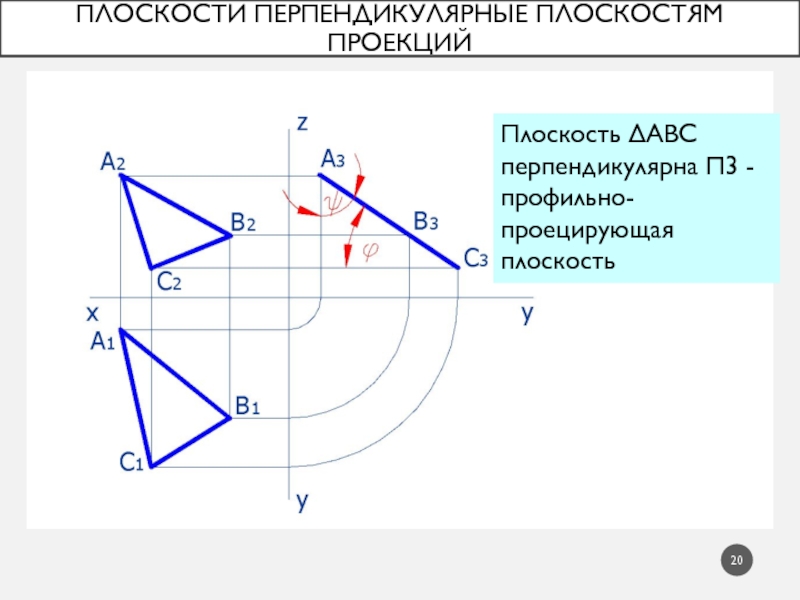
Слайд 20Плоскости перпендикулярные плоскостям проекций
Плоскость АВС перпендикулярна 3 - профильно-проецирующая плоскость
Слайд 22Особые линии плоскости.
Горизонталь плоскости
Горизонталь плоскости - прямая принадлежащая заданной
плоскости и параллельная плоскости проекций
Если плоскость задана следами, то горизонтальный
след плоскости - нулевая горизонталь этой плоскостиСлайд 23Особые линии плоскости.
Фронталь плоскости
Фронталь плоскости - прямая принадлежащая плоскости
и параллельная плоскости проекций
Если плоскость задана следами, то фронтальный след
плоскости - нулевая фронталь этой плоскостиСлайд 24Особые линии плоскости.
Горизонталь плоскости
AD принадлежит плоскости АВС
AD параллельна 1
AD
- горизонталь АВС
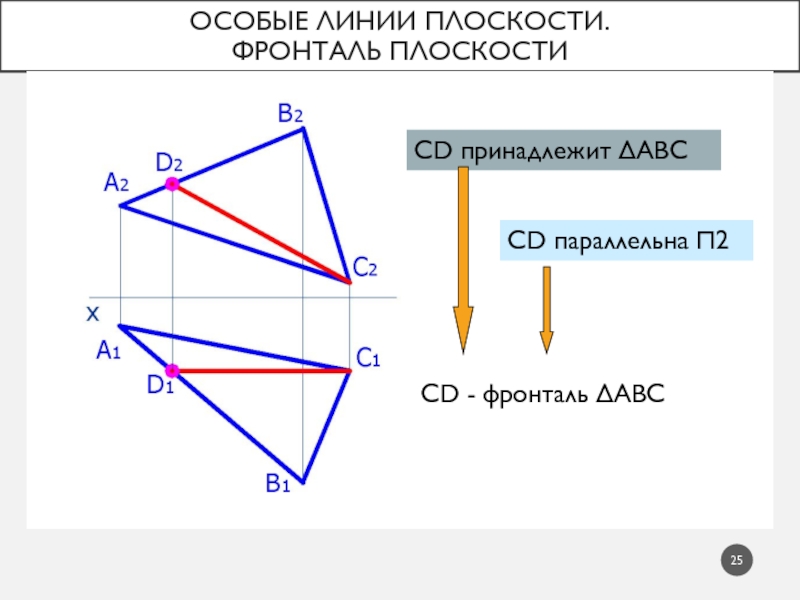
Слайд 25Особые линии плоскости.
Фронталь плоскости
CD принадлежит АВС
CD параллельна 2
CD -
фронталь АВС
Слайд 28Особые линии плоскости.
Линии наибольшего наклона плоскости
Линии наибольшего наклона заданной
плоскости к плоскости проекций - линии принадлежащие плоскости и перпендикулярные
горизонтали и фронтали плоскости :Линия наибольшего наклона плоскости к горизонтальной плоскости проекций называется линией ската
Линия наибольшего наклона плоскости к горизонтальной или профильной плоскости проекций не имеет другого названия
Слайд 29Особые линии плоскости.
Линии наибольшего наклона плоскости
Линии наибольшего наклона заданной
плоскости к плоскости проекций – линии, принадлежащие плоскости и перпендикулярные
горизонтали и фронтали плоскости :Линия наибольшего наклона плоскости к горизонтальной плоскости проекций называется линией ската
Линия наибольшего наклона плоскости к фронтальной плоскости проекций не имеет другого названия
Слайд 30Особые линии плоскости. Линия ската
MN принадлежит
MN перпендикулярна нулевой горизонтали
1
MN - линия ската
Из чего можно утверждать, что MN принадлежит
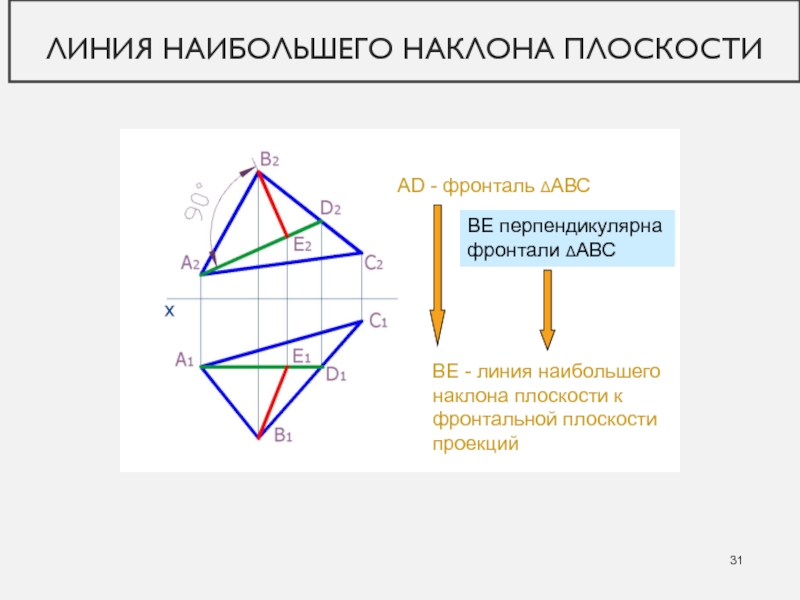
?Слайд 31Линия наибольшего наклона плоскости
AD - фронталь АВС
ВЕ - линия наибольшего
наклона плоскости к фронтальной плоскости проекций
ВЕ перпендикулярна фронтали АВС
Слайд 32Вопрос 5
Построение линии ската плоскости следует начинать с
Горизонтали
Фронтали
Следов
Профильной проекции
Слайд 33ВЫВОДЫ
Особые линии плоскости позволяют решать позиционные задачи для заданной плоскости
Особые
линии плоскости, принадлежащие ей:
горизонталь
фронталь
линия ската
линии наибольшего наклона плоскости
Особая линия
плоскости, имеющая одну общую точку с плоскостью - нормаль плоскостиСлайд 34Плоскость.
Позиционные и метрические задачи
Прямая может
принадлежать плоскости
пересекать плоскость под
некоторым углом
пересекать плоскость под прямым углом (быть перпендикулярна плоскости)
быть параллельна
плоскостиСлайд 35Особые линии плоскости. Нормаль
Нормаль - прямая перпендикулярная плоскости.
(не принадлежит плоскости,
имеет с ней одну общую точку).
Прямая перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся прямым этой плоскости.За эти две прямые, лежащие в одной плоскости, принимают горизонталь и фронталь плоскости, т.к. к ним можно провести линию под прямым углом.
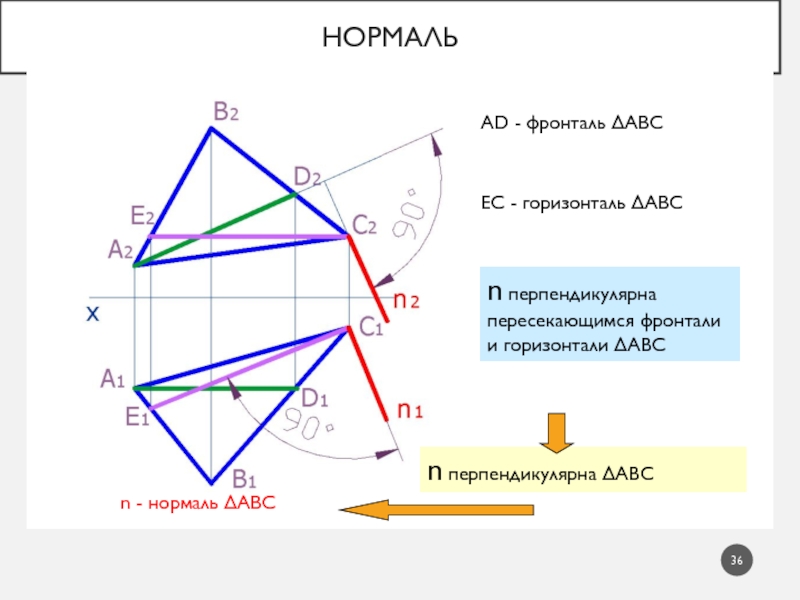
Слайд 36Нормаль
AD - фронталь АВС
ЕС - горизонталь АВС
n перпендикулярна пересекающимся фронтали
и горизонтали АВС
n перпендикулярна АВС
n - нормаль АВС
Слайд 37Нормаль
n перпендикулярна пересекающимся нулевым фронтали и горизонтали плоскости
n
перпендикулярна плоскости
n - нормаль плоскости
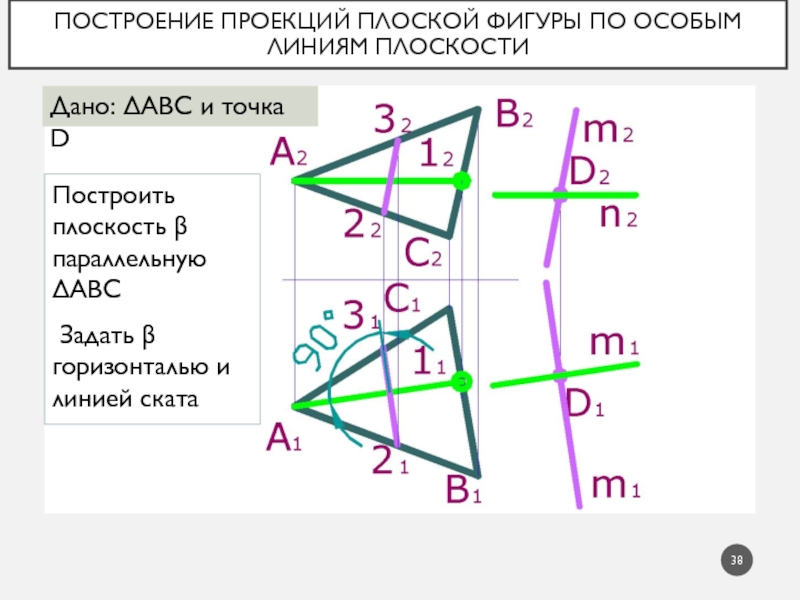
Слайд 38Построение проекций плоской фигуры по особым линиям плоскости
Дано: АВС и
точка D
Построить плоскость параллельную АВС
Задать горизонталью и
линией скатаСлайд 39Построение проекций плоской фигуры по особым линиям плоскости
Дано: АВС принадлежит
Угол АВС =90º
x(310,0,0)
Угол между следом 2 и осью
Х - 25ºУгол между следом 1 и осью Х - 30º
А(210,20,30)
AB=60мм ВС=65мм
АВ принадлежит горизонтали
Слайд 40Построение проекций плоской фигуры по особым линиям плоскости
Дано: (1, 2)
углы между следами и осью х
О(x,y,z) - центр окружности
Диаметр
окружностиСлайд 41ВЫВОДЫ
Особые линии плоскости позволяют решать позиционные задачи для заданной плоскости.
Особые
линии плоскости, принадлежащие ей:
- горизонталь;
- фронталь;
- линия ската;
- линии наибольшего
наклона плоскости.Особая линия плоскости, не принадлежащая ей - нормаль плоскости.