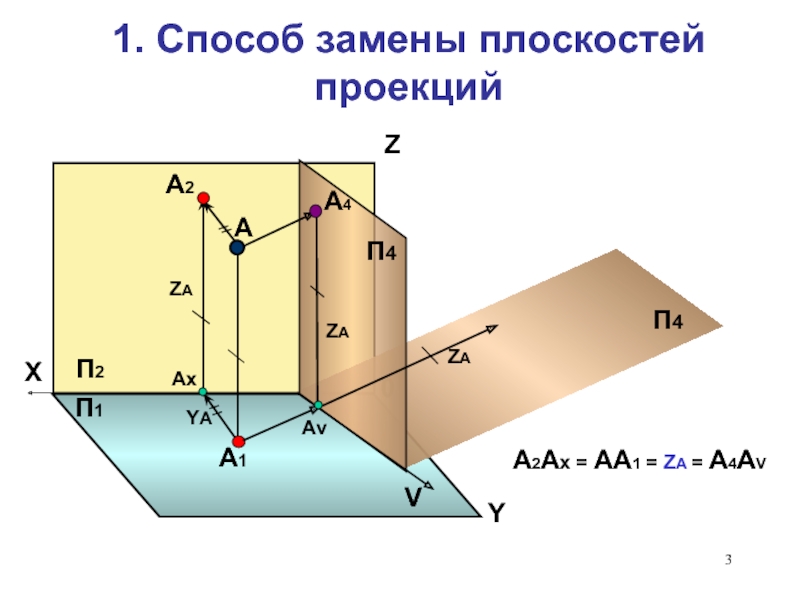
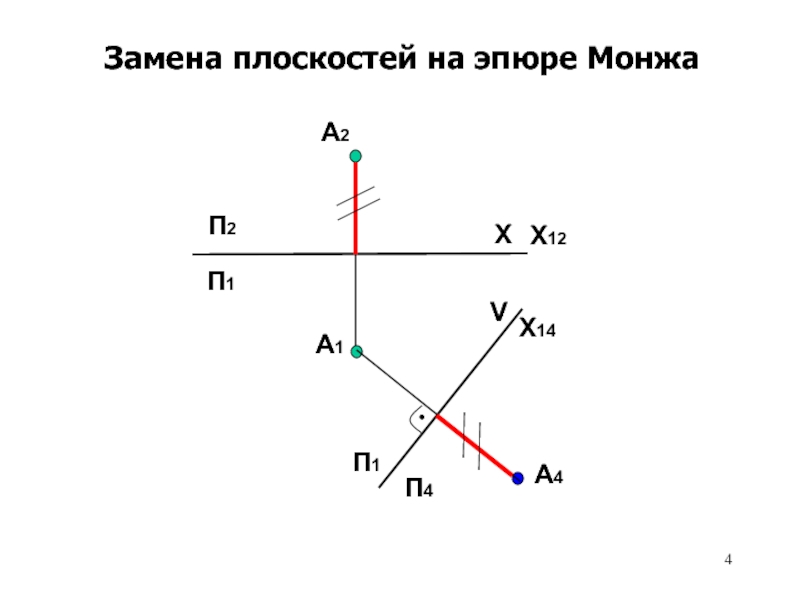
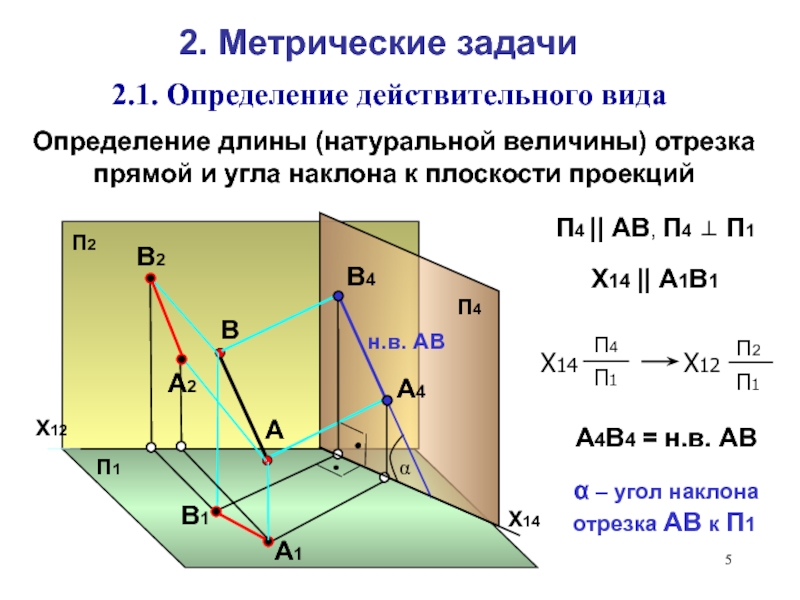
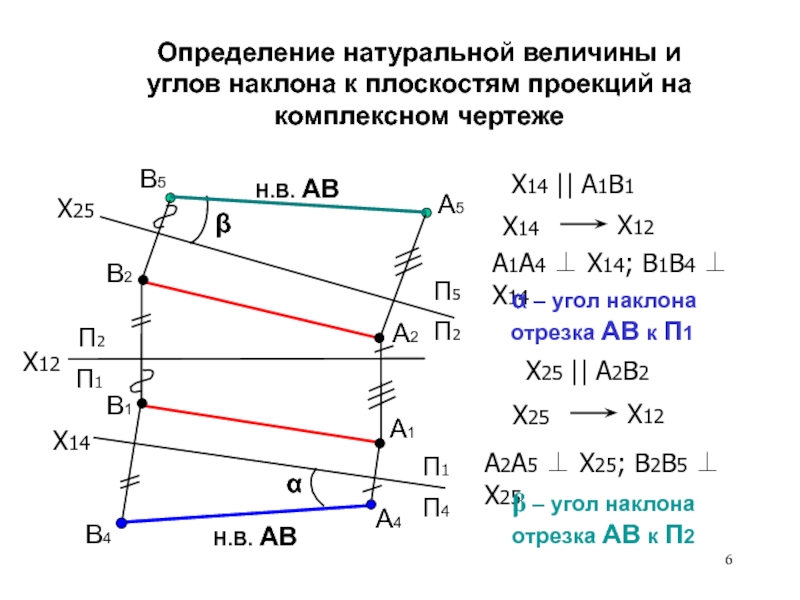
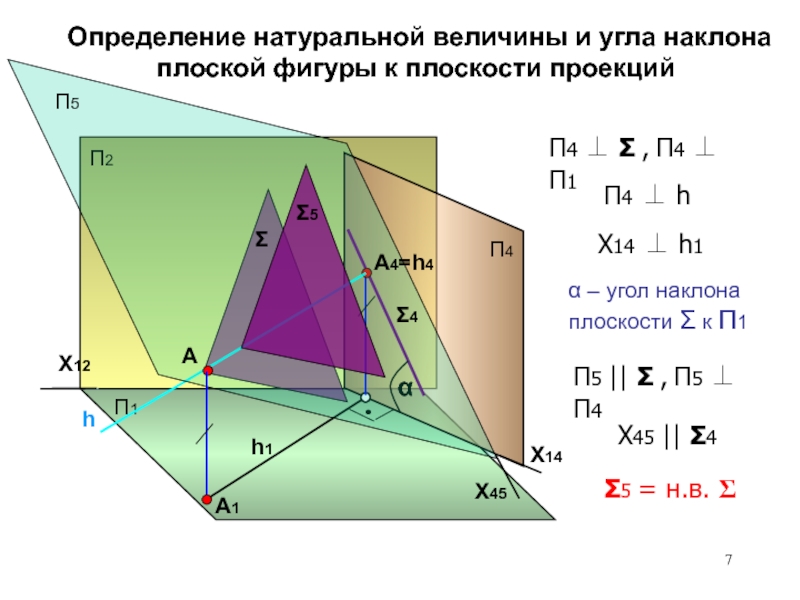
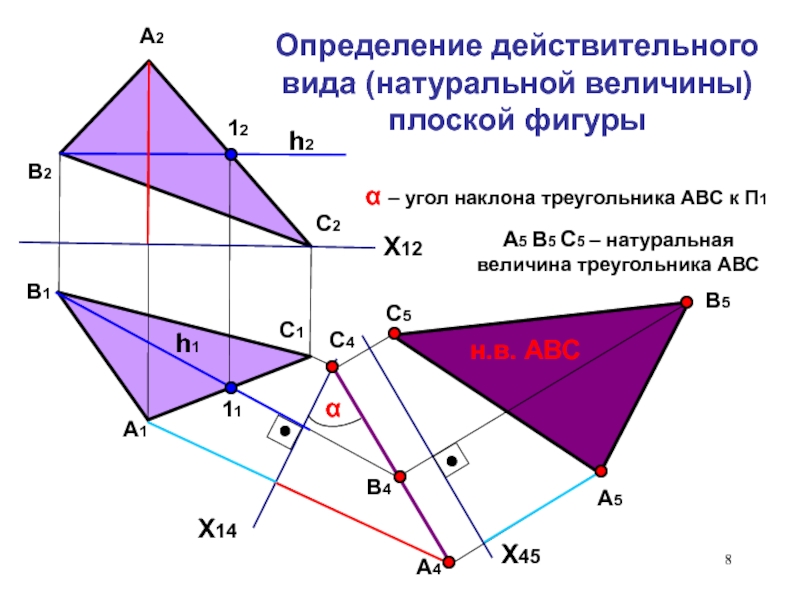
действительного вида.
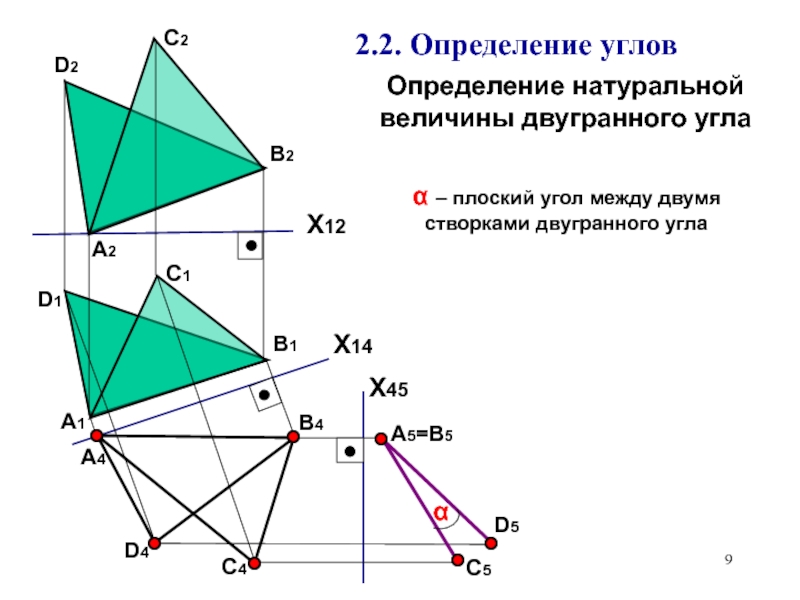
2.2. Определение углов.
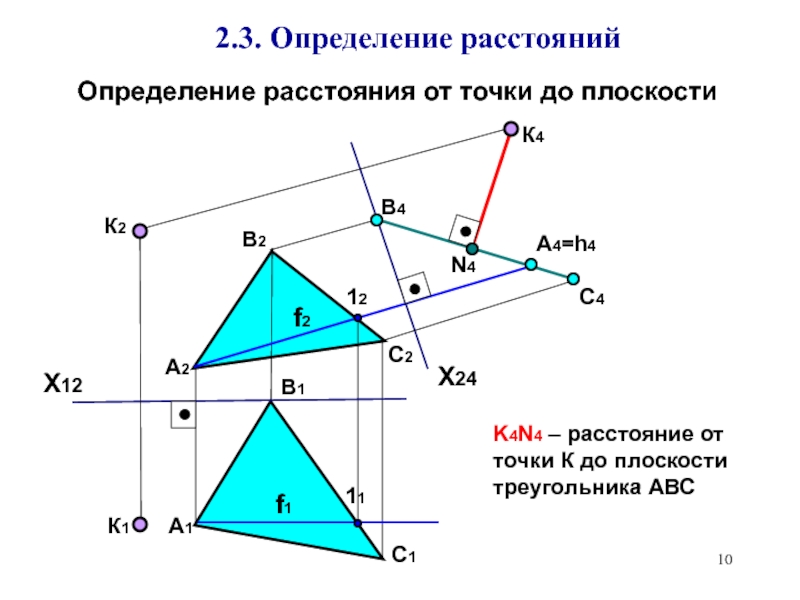
2.3. Определение расстояний.
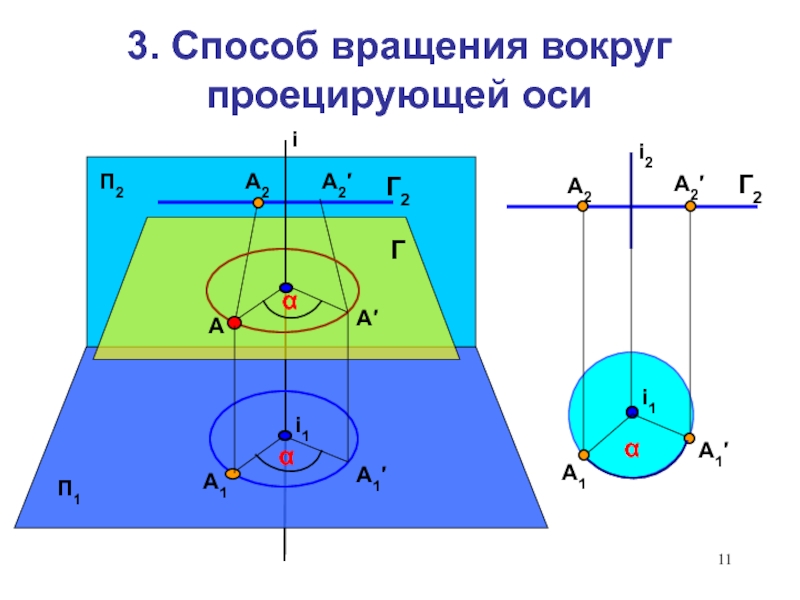
3.
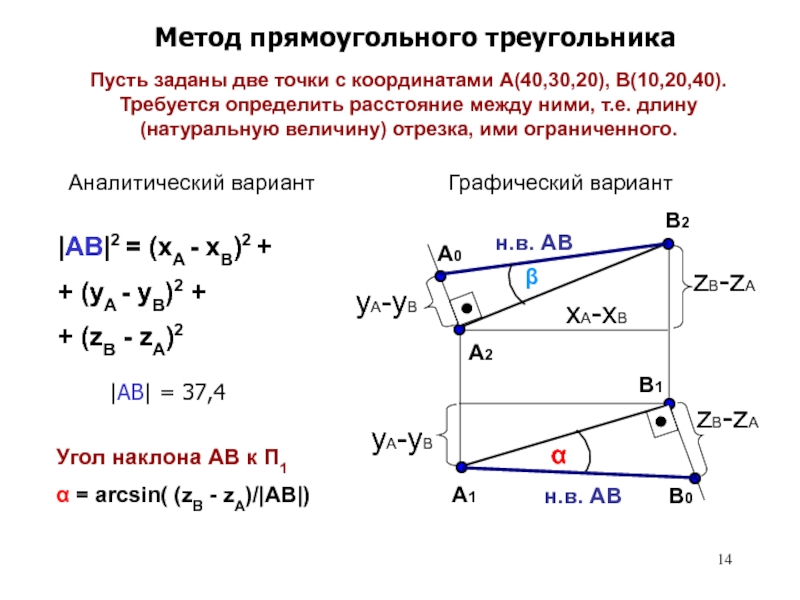
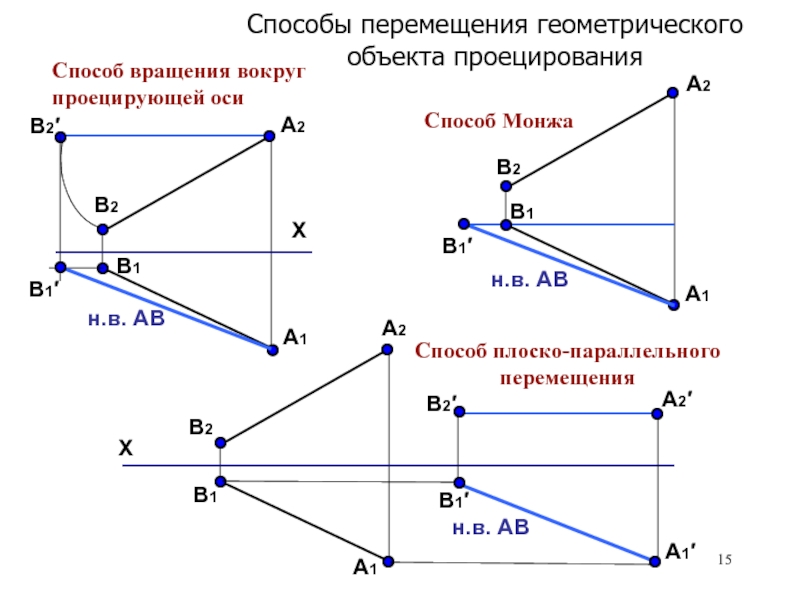
Способ вращения вокруг проецирующей оси.4. Определение длины отрезка прямой различными способами.
Лекция 3.
Способы преобразования чертежа