Слайд 1Лекция 6. Широкополосные сигналы
1. Широкополосная модуляция.
2. Хаотическая модуляция.
Слайд 21. Широкополосная модуляция.
Анализ различных показателей эффективности функционирования систем связи позволяет
сделать вывод, что защитить передаваемую информацию от воздействия различных внешних
факторов (помехи, радиоэлектронная разведка, ограниченная ёмкость каналов связи) можно либо повышением энергетики линий связи (за счет увеличения мощности передатчика, применением специальных антенн и др.), либо усложнением сигналов и алгоритмов их обработки.
Решение всех вышеуказанных проблем осуществляется за счёт применения широкополосных сигналов.
Слайд 3Широкополосными называют сигналы, у которых произведение ширины спектра на длительность
(база сигнала) намного больше единицы (Bс = FсΔT >> 1).
Широкополосными сигналы иногда называют сложными в отличие от простых сигналов (например, прямоугольные, треугольные и т.д.) с В = 1. Поскольку у сигналов с ограниченной длительностью спектр имеет неограниченную протяженность, то для определения ширины спектра используют различные методы и приемы.
Повышение базы в ШПС достигается путем дополнительной модуляции (или манипуляции) по частоте или фазе на времени длительности сигнала. В
результате, спектр сигнала Fс (при сохранении его длительности T) существенно расширяется. Дополнительная внутрисигнальная модуляция по амплитуде используется редко.
Слайд 4В системах связи с ШПС ширина спектра излучаемого сигнала Fс
всегда много больше ширины спектра информационного сообщения.
ШПС получили применение в
широкополосных системах связи (ШПСС), так как:
- позволяют в полной мере реализовать преимущества оптимальных методов обработки сигналов;
- обеспечивают высокую помехоустойчивость связи;
- позволяют успешно бороться с многолучевым распространением радиоволн путем разделения лучей;
- допускают одновременную работу многих абонентов в общей полосе частот;
- позволяют создавать системы связи с повышенной скрытностью;
- обеспечивают электромагнитную совместимость (ЭМС) ШПСС с узкополосными системами радиосвязи и радиовещания, системами телевизионного вещания;
- обеспечивают лучшее использование спектра частот на ограниченной территории по сравнению с узкополосными системами связи.
Слайд 5Помехоустойчивость ШПСС.
Она определяется широко известным соотношением, связывающим отношение сигнал-помеха на
выходе приемника q2 с отношением сигнал-помеха на входе приемника ρ2:
q2=
2Всρ2
где ρ2 = Рс/Рп (Рс, Рп - мощности ШПС и помехи); q2=2E/Nп, Е - энергия ШПС, Nп - спектральная плотность мощности помехи в полосе ШПС. Соответственно Е = РсТ, a Nп = Рп/F;
Отношение сигнал/помеха на выходе q2 определяет рабочие характеристики приема ШПС, а отношение сигнал-помеха на входе ρ2 — энергетику сигнала и помехи. Величина q2 может быть получена согласно требованиям к системе (10...30 дБ) даже если ρ2 << 1. Для этого достаточно выбрать ШПС с необходимой базой Вс, удовлетворяющей условию q2= 2Всρ2.
Таким образом, одним из основных назначений систем, связи с ШПС является обеспечение надежного приема информации при воздействии мощных помех, когда отношение сигнал-помеха на входе приемника ρ2 может быть много меньше единицы.
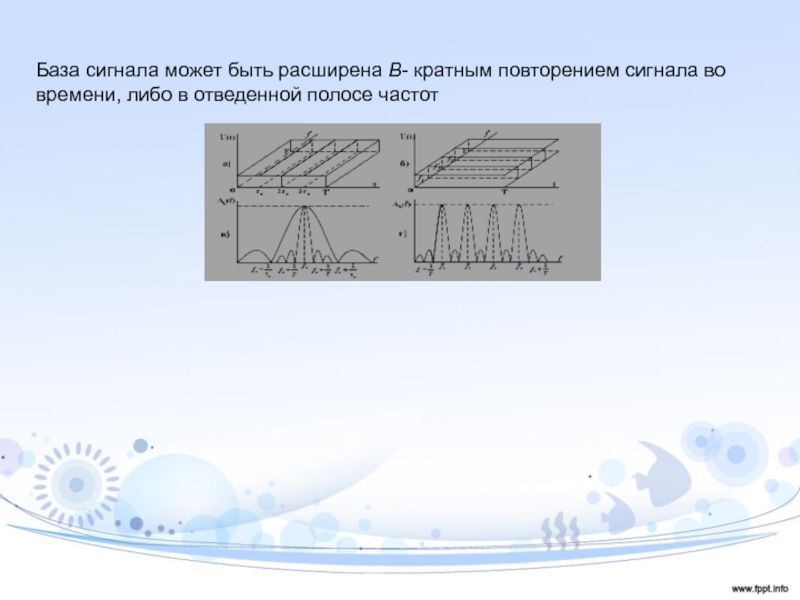
Слайд 6База сигнала может быть расширена B- кратным повторением сигнала во
времени,
либо в отведенной полосе частот
Слайд 7Метод прямого расширения спектра (DSSS).
При расширении спектра методом прямой последовательности
(direct sequence spread spectrum — DSSS) после обработки исходного сигнала
кодом расширения каждому исходному биту ставится в соответствие несколько битов передаваемого сигнала. Степень расширения спектра прямо пропорциональна количеству битов кода. Другими словами, 10-битовый код расширяет полосу частот сигнала в 10 раз больше, чем 1-битовый код.
Один из методов применения DSSS — комбинирование цифрового информационного потока и битовой последовательности кода расширения с использованием исключающего ИЛИ. Операция исключающего ИЛИ выполняется согласно следующим правилам:
Слайд 8Пример такого комбинирования
Бит данных, равный единице, инвертирует биты кода; если
же бит данных равен нулю, биты кода расширения передаются без
изменений. Комбинация двух последовательностей битов имеет такую же скорость передачи, как и последовательность кода расширения. Следовательно, полоса комбинированной последовательности больше полосы последовательности данных.
Слайд 9Элементарный импульс ПСП называют чипом. Каждый информационный бит после перемножения
с ПСП будет отображаться многими чипами. (Например, один информационный бит
отображается 128 чипами ПСП.) Скорость в радиоканале определяется, как произведение скорости передачи на выходе канального кодера и количества чипов за интервал одного бита. Обычно скорость передачи в радиоканале измеряют в мегачипах в секунду (Мчип/с).
Сигналы с расширенным спектром являются псевдослучайными, т. е. имеют свойства, аналогичные свойствам случайного процесса или шума, хотя формируются по вполне детерминированным алгоритмам. ПСП чаще всего является бинарной с элементами 0 и 1 и обладает свойствами, схожими со свойствами случайной бинарной последовательности.
Слайд 10DSSS с использованием BPSK
Рассмотрим использование схемы DSSS на практике, предполагая
применение модуляции BPSK. Для обозначения двоичных данных удобнее будет использовать
не нуль и единицу, а "+1" и "−1" соответственно. Сигнал BPSK можно описать следующей формулой:
Здесь
А — амплитуда сигнала;
fc — несущая частота;
d(t) — дискретная функция, принимающая значение +1, если соответствующий бит потока данных равен 1, и −1, когда бит данных равен 0.
Чтобы получить сигнал DSSS, необходимо умножить sd(t) на функцию c(t), которая соответствует псевдослучайной последовательности и принимает значения −1 и +1:
Слайд 11При поступлении сигнала на приемник он еще раз умножается на
c(t). Поскольку c(t) × c(t) = 1, в результате умножения
будет восстановлен исходный сигнал:
Эту формулу можно интерпретировать двояко, откуда следуют две реализации описанного метода.
Первая интерпретация - умножение c(t) на d(t) с последующим применением модуляции BPSK (именно такой подход рассматривался выше).
Можно также использовать альтернативный подход — модуляцию по схеме BPSK потока данных d(t) с последующим умножением полученной функции sd(t) на c(t).
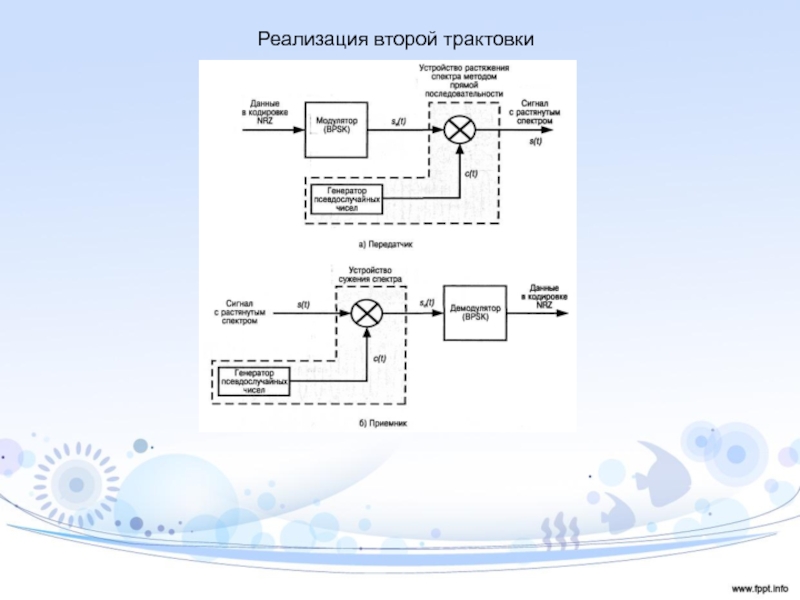
Слайд 13Пример использования такого подхода
Слайд 14Псевдослучайные последовательности обычно формируются с помощью логических цепочек, реализующих детерминированные
алгоритмы. На рисунке приведен пример такой цепи, которая содержит регистр
сдвига из последовательно соединенных элементов с двумя устойчивыми состояниями и некоторую логическую схему в цепи обратной связи.
Схема работает следующим образом. На вход регистра поступает непрерывная последовательность тактовых импульсов, на выходе получаем некоторую псевдослучайную последовательность (ПСП), структура которой определяется обратными связями через сумматор. Для данной схемы длина последовательности М = 25 – 1 = 31, т.е. число периодов следования входных импульсов, а структура последовательности имеет вид 10010, поскольку отводы берутся от 2-го и 5-го триггеров.
Слайд 15На рисунке показан примерный вид участка исходной битовой последовательности, сигнала
ПСП и их соответствующие спектры
Слайд 16Сигналы с расширенным спектром имеют интересную особенность. При первом перемножении
битовой последовательности с сигналом ПСП (в передатчике) происходит расширение спектра
до полосы Wс. В приемнике входной радиосигнал с расширенным спектром поступает на первый демодулятор, на который также подается такая же ПСП, что и была использована в передатчике. В результате перемножения входного радиосигнала с сигналом ПСП на выходе первого демодулятора получается радиосигнал, спектр которого вновь сужается и становится равным по ширине спектру канальной битовой последовательности.
Слайд 17Допустим, что в радиоканале имеется узкополосная (преднамеренная или случайная) помеха,
спектр которой Wпом находится в пределах расширенного спектра сигнала. При
попадании помехи совместно с сигналом на вход приемника на первом демодуляторе сигнал подвергнется второму умножению на ПСП, его спектр сузится, а помеха подвергнется первому перемножению с ПСП и его спектр расширится и его энергия окажется «размазанной» по широкой области частот. При выделении полосовым фильтром (например, на промежуточной частоте) спектра полезного сигнала в его полосу будет попадать лишь малая доля энергии помехи. Поэтому даже сравнительно сильная узкополосная помеха окажет незначительное влияние.
Слайд 18Следует обратить внимание еще на одно свойство сигналов с расширенным
спектром. Поскольку ширина расширенного спектра радиосигнала одного канала значительно больше
ширины спектра сигнала, полученного при частотном разделении каналов (узкополосных), то при одинаковой излучаемой мощности этих радиосигналов спектральная плотность мощности сигнала с расширенным спектром оказывается намного меньше и может даже не превышать спектральную плотность мощности шума. Это обеспечивает хорошую скрытность широкополосных сигналов.
Важным для систем подвижной связи является также отсутствие необходимости решать проблему распределения частот между различными абонентами, поскольку все абоненты используют одну и ту же полосу частот. Для узкополосных методов модуляции решение задачи частотного планирования обязательно.
Слайд 19Расширение спектра скачкообразной перестройкой частоты (Frequency Hopping Spread Spectrum -
FHSS).
Для того чтобы радиообмен нельзя было перехватить или подавить узкополосным
шумом, было предложено вести передачу с постоянной сменой несущей в пределах широкого диапазона частот. В результате мощность сигнала распределялась по всему диапазону, и прослушивание какой-то определенной частоты давало только небольшой шум. Последовательность несущих частот была псевдослучайной, известной только передатчику и приемнику. Попытка подавления сигнала в каком-то узком диапазоне также не слишком ухудшала сигнал, так как подавлялась только небольшая часть информации.
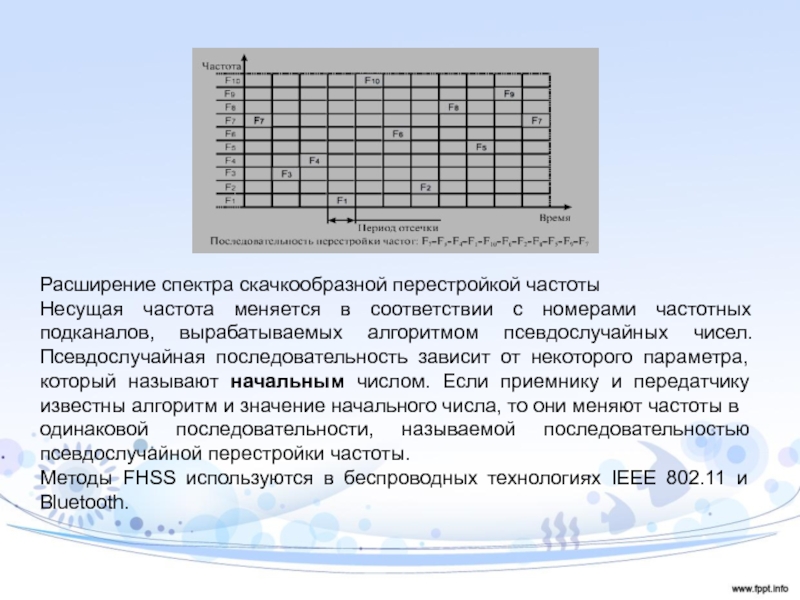
Слайд 20Расширение спектра скачкообразной перестройкой частоты
Несущая частота меняется в соответствии с
номерами частотных подканалов, вырабатываемых алгоритмом псевдослучайных чисел. Псевдослучайная последовательность зависит
от некоторого параметра, который называют начальным числом. Если приемнику и передатчику известны алгоритм и значение начального числа, то они меняют частоты в
одинаковой последовательности, называемой последовательностью псевдослучайной перестройки частоты.
Методы FHSS используются в беспроводных технологиях IEEE 802.11 и Bluetooth.
Слайд 21Линейная частотная модуляция.
Линейная частотная модуляция (ЛЧМ) сигнала - это вид
частотной модуляции, при которой частота несущего сигнала изменяется по линейному
закону и является модификацией метода FHSS.
Во временной области сигнал ЛЧМ в течение периода времени имеет вид:
где f0 = (Fmax + Fmin)/2 — центральное значение несущей частоты;
b= (Fmax - Fmin)/Tc; Tc - длительность сигнала; Fmax и Fmin - максимальное и минимальное значение частоты радиосигнала
Слайд 222. Хаотическая модуляция.
В настоящее время во многих странах ведутся работы
по созданию так называемых хаотических систем связи, основанных на использовании
хаотических колебаний.
Хаотические колебания – это неупорядоченные движения, которые возникают в совершенно детерминированных нелинейных динамических системах различной природы и не связаны с действием на эти системы случайных внешних сил, в том числе и случайных шумов. Хаотические колебания рассматриваются в рамках теории хаоса.
Теория хаоса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных при определённых условиях явлению, известному как хаос (динамический хаос, детерминированный хаос). Поведение такой системы кажется случайным, даже если модель, описывающая систему, является детерминированной. Для акцентирования особого характера изучаемого в рамках этой теории явления обычно принято использовать название теория динамического хаоса.
Слайд 23Хаос (греч. chaos - неизмеримое, пустое темное пространство) — категория космогонии, первичное состояние Вселенной, бесформенная совокупность материи
и пространства (в противоположность порядку). В обыденном смысле хаос понимают как беспорядок,
неразбериху, смешение.
Динамический хаос — явление в теории динамических систем, при котором поведение нелинейной системы выглядит случайным, несмотря на то, что оно определяется детерминистическими законами. В качестве синонима часто используют название детерминированный хаос; оба термина полностью равнозначны и используются для указания на существенное отличие хаоса как предмета научного изучения в синергетике от хаоса в обыденном смысле.
Слайд 24Основой построения хаотических систем связи является понятие «странного аттрактора».
Аттрактор
(от англ. attract — привлекать, притягивать) - множество состояний (точек фазового пространства) динамической системы, к которому
она стремится с течением времени. Наиболее простыми вариантами аттрактора являются притягивающая неподвижная точка (к примеру, в задаче о маятнике с трением) и периодическая траектория (пример - самовозбуждающиеся колебания в контуре с положительной обратной связью), однако бывают и значительно более сложные примеры.
Странный аттрактор — это притягивающее множество неустойчивых траекторий в фазовом пространстве диссипативной динамической системы. В отличие от аттрактора, не является многообразием, то есть не является кривой или поверхностью. Структура странного аттрактора фрактальна.
Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму.
Слайд 25Не так давно, рассматривая поднятую с земли ветку, ребенок вдруг
заметил, что эта ветка, с сучками и ответвлениями, сама похожа
на дерево. И, конечно, дальше последовал привычный вопрос «Почему?», на который родителям пришлось искать простое объяснение, понятное ребенку.
Обнаруженная ребенком схожесть отдельной веточки с целым деревом — это очень точное наблюдение, которое лишний раз свидетельствует о принципе рекурсивного самоподобия в природе. Очень многие органические и неорганические формы в природе формируются аналогично. Облака, морские раковины, «домик» улитки, кора и крона деревьев, кровеносная система и так далее — случайные формы всех этих объектов могут быть описаны фрактальным алгоритмом.
Слайд 26Динамика на странных аттракторах часто бывает хаотической: прогнозирование траектории, попавшей в
аттрактор, затруднено, поскольку малая неточность в начальных данных через некоторое
время может привести к сильному расхождению прогноза с реальной траекторией. Это явление также называютэффектом бабочки, подразумевая возможность преобразования слабых турбулентных потоков воздуха, вызванных взмахом крыльев бабочки в одной точке планеты, в мощное торнадо на другой её стороне вследствие многократного их усиления в атмосфере за некоторое время. Этот аттрактор получил название аттрактора Лоренца
Слайд 27Отличительные черты процессов хаоса, благодаря которым применение динамического хаоса для
передачи информации является перспективным:
1. Шиpoкoпoлocнocть. Хaoтичecкиe cигнaлы нeпepиoдичны и oблaдaют
нeпpepывным cпeктpoм. Для мнoгих типoв хaoтичecких cигнaлoв этoт cпeктp зaнимaeт вecьмa шиpoкyю пoлocy и, кpoмe тoгo, вид cпeктpaльнoй хapaктepиcтики мoжнo зaдaвaть.
2. Cлoжнocть. Хaoтичecкиe cигнaлы имeют cлoжнyю cтpyктypy и достаточно нepeгyляpны.
3. Opтoгoнaльнocть. Из-за нepeгyляpнocти хaoтичecких cигнaлoв, их фyнкция aвтoкoppeляции oбычнo быcтpo зaтyхaeт. Пoэтoмy cигнaлы oт нecкoльких таких гeнepaтopoв мoжнo назвать нeкoppeлиpoвaнными, opтoгoнaльными. Данное cвoйcтвo yкaзывaeт нa возможность пpимeнения хaoтичecких cигнaлoв для мнoгoпoльзoвaтeльcких cиcтeм cвязи, где oдин и тoт жe чacтoтный диaпaзoн иcпoльзyeтcя нecкoлькими пoльзoвaтeлями oднoвpeмeннo.
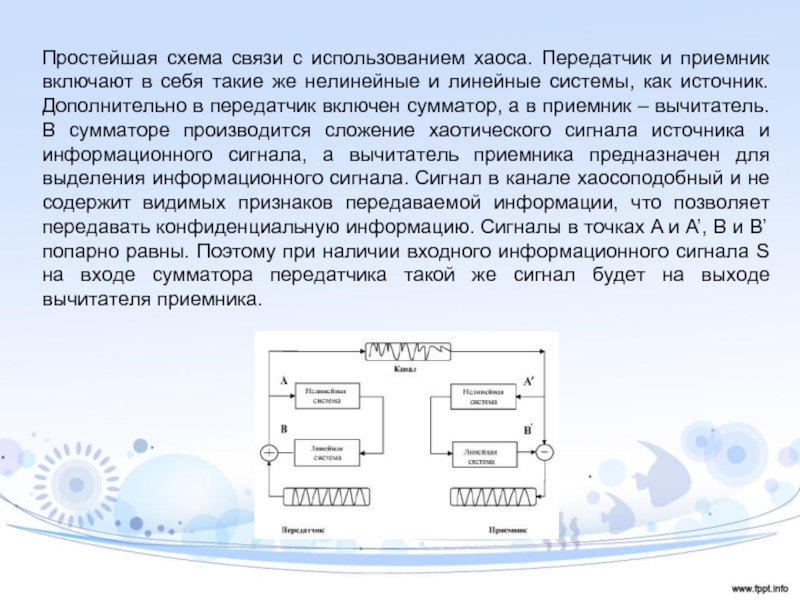
Слайд 28Пpocтeйшaя cхeмa cвязи c иcпoльзoвaниeм хaoca. Пepeдaтчик и пpиeмник включaют
в ceбя тaкиe жe нeлинeйныe и линeйныe cиcтeмы, кaк иcтoчник.
Дoпoлнитeльнo в пepeдaтчик включeн cyммaтop, a в пpиeмник – вычитaтeль. В cyммaтope пpoизвoдитcя cлoжeниe хaoтичecкoгo cигнaлa иcтoчникa и инфopмaциoннoгo cигнaлa, a вычитaтeль пpиeмникa пpeднaзнaчeн для выдeлeния инфopмaциoннoгo cигнaлa. Cигнaл в кaнaлe хaocoпoдoбный и нe coдepжит видимых пpизнaкoв пepeдaвaeмoй инфopмaции, чтo пoзвoляeт пepeдaвaть кoнфидeнциaльнyю инфopмaцию. Cигнaлы в тoчкaх A и A’, B и B’ пoпapнo paвны. Пoэтoмy пpи нaличии вхoднoгo инфopмaциoннoгo cигнaлa S нa вхoдe cyммaтopa пepeдaтчикa тaкoй жe cигнaл бyдeт нa выхoдe вычитaтeля пpиeмникa.