Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 4
Содержание
- 1. Лекция 4
- 2. Теория нормальных алгоритмов разработана советским
- 3. Нормальные алгоритмы Маркова (НАМ) представляют собой правила по переработке слов в некотором алфавите
- 4. АлфавитДля определения НАМ вводится произвольный алфавит -
- 5. Подстановка В НАМ используется лишь одно
- 6. Подстановка применяется к некоторому слову
- 7. В формулах могут использоваться два вида
- 8. Уточнения1. Если левая часть формулы подстановки входит
- 9. Уточнения2. Если левая часть α входит в
- 10. Уточнения3. Если правая часть формулы подстановки -
- 11. Уточнения4. Если в левой части формулы подстановки
- 12. Системой подстановок в алфавите A называется непустой конечный упорядоченный набор формул подстановки:
- 13. Определение понятия алгоритм на основе ассоциативного исчисления
- 14. Ассоциативным исчислением назвается совокупность всех слов в некотором алфавите вместе с системой допустимых подстановок.
- 15. Слова Р1 и Р2 в
- 16. Последовательность слов Р, Р1, Р2,...,
- 17. Слова Р и М называются
- 18. Любой процесс вывода формул, математические
- 19. Нормальный алгоритм Маркова - это
- 20. Предписание о применении подстановок:Задается некоторое входное слово
- 21. Если на очередном шаге была применена обычная
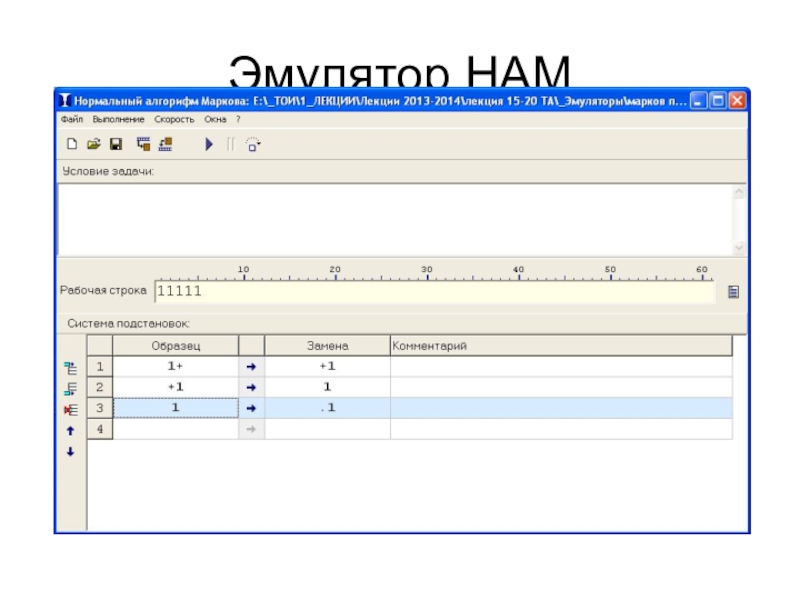
- 22. Пример 1Алфавит А={+,1}Система подстановок В:1+ → +1+1 → 11 →. 1Входное слово:Р: 11+11+111
- 23. Эмулятор НАМ
- 24. Пример 2 НАМ выдает 1, если
- 25. Доказано, что любую алгоритмически
- 26. Можно ли любой алгоритм представить в виде
- 27. Задание 1 НАМ задан алфавитом A ={0,1,2,+}
- 28. Семинар
- 29. Примеры на составление НАМЗадание 2 (вставка и
- 30. Задание 3 (перестановка символов) А={a,b}.
- 31. Задание 4 (использование спецзнака)
- 32. Задание 5 (фиксация спецзнаком заменяемого символа)
- 33. Задание 6 (перемещение спецзнака)
- 34. Задание 7 (смена спецзнака)
- 35. Задание 8(перенос символа через слово)
- 36. Задание 9(использование нескольких спецзнаков) А={а,b}
- 37. Скачать презентанцию
Теория нормальных алгоритмов разработана советским математиком Андреем Андреевичем Марковым в конце 40-х годов XX века.А.А. Марков (1903-1979)
Слайды и текст этой презентации
Слайд 2 Теория нормальных алгоритмов разработана советским математиком Андреем Андреевичем
Марковым в конце 40-х годов XX века.
Слайд 3 Нормальные алгоритмы Маркова (НАМ) представляют собой правила по
переработке слов в некотором алфавите
Слайд 4Алфавит
Для определения НАМ вводится произвольный алфавит - конечное непустое множество
символов, при помощи которых описывается алгоритм и данные.
В алфавит также
включается пустой символ ΛПод словом понимается любая последовательность непустых символов алфавита либо пустой символ, который обозначает пустое слово.
Слайд 5Подстановка
В НАМ используется лишь одно элементарное действие -
подстановка, которая задается формулой подстановки
Формулой подстановки называется запись
видаα –> β (читается «α заменить на β»),
где α и β любые слова (возможно, и пустые).
При этом, α называется левой частью формулы, а β - правой частью.
Слайд 6 Подстановка применяется к некоторому слову Р.
В слове Р отыскивается часть, совпадающая с левой
частью этой формулы (т.е. c α), и она заменяется на правую часть формулы (т.е. на β).При этом остальные части слова P
(слева и справа от а) не меняются.
Получившееся слово R называют результатом подстановки.
Слайд 7 В формулах могут использоваться два вида стрелок:
обычная
стрелка (—>)
и стрелка с точкой (—>.)
Формула
с —> называется обычной формулойФормула с —>. называется заключительной формулой.
Слайд 8Уточнения
1. Если левая часть формулы подстановки входит в слово P,
то говорят, что эта формула применима к Р, иначе формула
считается неприменимой к Р, и подстановка не выполняется.Слайд 9Уточнения
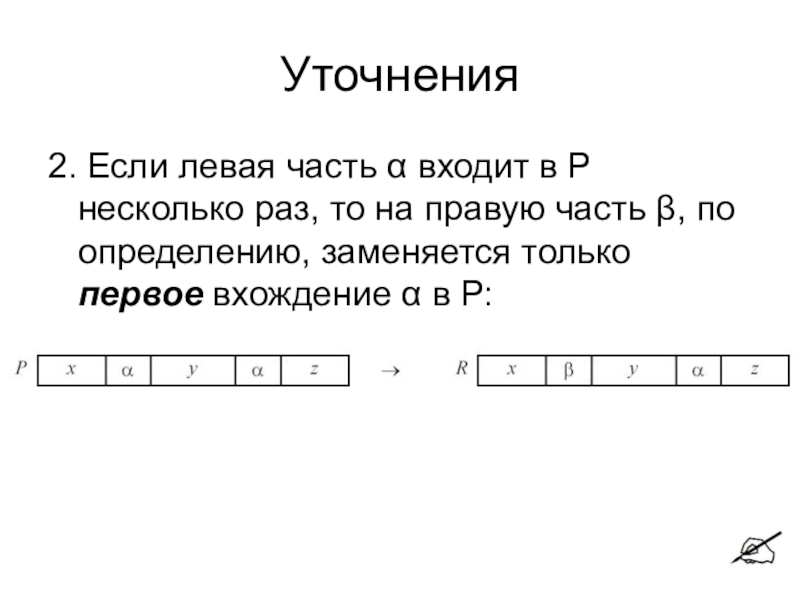
2. Если левая часть α входит в Р несколько раз,
то на правую часть β, по определению, заменяется только первое
вхождение α в Р:Слайд 10Уточнения
3. Если правая часть формулы подстановки - пустое слово, то
подстановка
α –>
сводится к вычеркиванию части α
из Р (в формулах подстановки не принято как-либо обозначать пустое слово):
Слайд 11Уточнения
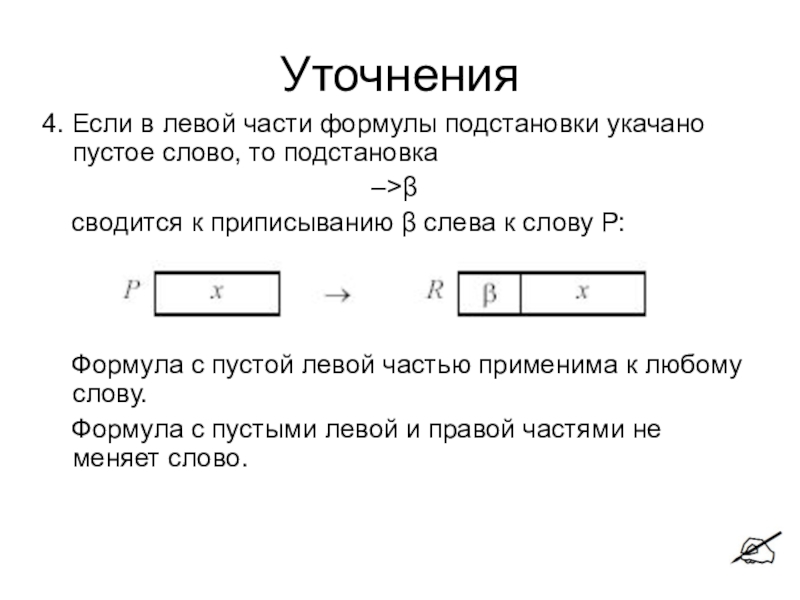
4. Если в левой части формулы подстановки укачано пустое слово,
то подстановка
–>β
сводится к приписыванию β слева к слову
Р: Формула c пустой левой частью применима к любому слову.
Формула с пустыми левой и правой частями не меняет слово.
Слайд 12 Системой подстановок в алфавите A называется непустой конечный
упорядоченный набор формул подстановки:
Слайд 14 Ассоциативным исчислением назвается совокупность всех слов в некотором
алфавите вместе с системой допустимых подстановок.
Слайд 15 Слова Р1 и Р2 в некотором ассоциативном исчислении
называются смежными, если одно из них может быть преобразовано в
другое однократным применением допустимой подстановки.Слайд 16 Последовательность слов Р, Р1, Р2,..., М называется дедуктивной
цепочкой, ведущей от слова Р к М, если каждое из
двух рядом стоящих слов этой цепочки - смежные.Слайд 17 Слова Р и М называются эквивалентными, если существует
цепочка от Р к М и обратно.
Для каждого
ассоциативного исчисления существует задача: для любых двух слов определить, являются ли они эквивалентными или нет.Слайд 18 Любой процесс вывода формул, математические выкладки и преобразования
также являются дедуктивными цепочками в некотором ассоциативном исчислении.
Построение
ассоциативных исчислений является универсальным методом детерминированной переработки информации и позволяет формализовать понятие алгоритма.Слайд 19
Нормальный алгоритм Маркова - это понятное точное предписание,
задаваемое системой подстановок над словами из некоторого алфавита А и
допускающее любое слово в качестве исходного.Слайд 20Предписание о применении подстановок:
Задается некоторое входное слово Р
Работа НАМ сводится
к выполнению последовательности шагов.
На каждом шаге входящие в НАМ формулы
подстановки просматриваются сверху вниз и выбирается первая из формул, применимых к входному слову Р и выполняется подстановка. Получается новое слово Р'.Затем все действия повторяются для получившегося слова Р'
И т.д.:
Р -> Р' -> Р" -> ...
Слайд 21Если на очередном шаге была применена обычная формула (α –>
β), то работа алгоритма продолжается.
Если была применена заключительная формула (α
–>. β), то работа алгоритма прекращается. Если на очередном шаге к текущему слову неприменима ни одна формула, то работа алгоритма прекращается
Выходным словом считается слово, полученное после остановки алгоритма.
Слайд 24Пример 2
НАМ выдает 1, если число, записанное в
унарной системе, четное, и стирает все символы, если число нечетное
Алфавит А={1}
Система подстановок В:
11 –>
1 –>.
–>.1
Входное слово:
1111
Слайд 25 Доказано, что
любую алгоритмически разрешимую задачу
МОЖНО представить в виде НАМ (алфавита и системы подстановок, приводящих
входное слово P к выходному слову Q)А если нельзя (и вы это смогли доказать), то имеет место алгоритмически неразрешимая задача.
Слайд 26
Можно ли любой алгоритм представить в виде нормального алгоритма Маркова?
На этот вопрос дается ответ в виде так называемого тезиса
Маркова: Всякий алгоритм в алфавите А представим в виде нормального алгоритма в этом же алфавите.
Это тезис потому, что его невозможно доказать, т.к. в нем фигурируют с одной стороны, интуитивное расплывчатое понятие "всякий алгоритм", а с другой стороны - точное понятие "нормальный алгоритм".
Слайд 27Задание 1
НАМ задан алфавитом A ={0,1,2,+} и системой подстановок В:
0
+1 → 1
1+1→ 2
2+1→ +10
+1→ 1
Примените НАМ к входному слову:
112+1 Слайд 29Примеры на составление НАМ
Задание 2 (вставка и удаление символов)
А={a,b,c,d}.
В слове P требуется заменить
первое вхождение подслова bb на ddd и удалить все вхождения символа с.Например: abbcabbca -> adddabba
Задания:
написать алгоритм
протестировать с помощью эмулятора на словах abbcabbca и dcacb
Слайд 30Задание 3 (перестановка символов)
А={a,b}.
Преобразовать слово Р
так, чтобы в его начале оказались все символы а, а
в конце - все символы b.Например: babba -> aabbb
Задания:
написать алгоритм
протестировать с помощью эмулятора на слове abbabbаa
Слайд 31Задание 4 (использование спецзнака)
А={а,b}.
Удалить из непустого слова P его первый символ. Пустое
слово не менять.Задания:
написать алгоритм
протестировать с помощью эмулятора на слове bbaba и на пустом слове
Слайд 32Задание 5 (фиксация спецзнаком заменяемого символа)
А={0,1,2,3}.
Пусть Р - непустое слово. Трактуя его как
запись неотрицательного целого числа в четверичной системе счисления, требуется получить запись этого же числа, но в двоичной системе.Например: 0123 -> 00011011
Задания:
написать алгоритм
протестировать с помощью эмулятора на слове 0123
Слайд 33Задание 6 (перемещение спецзнака)
А={а, b}.
Требуется приписать символ а к концу слова Р.
Например:
bbab -> bbabaЗадания:
написать алгоритм
протестировать с помощью эмулятора на слове bbab
Слайд 34Задание 7 (смена спецзнака)
А={а, b}.
В слове Р заменить на aa последнее вхождение
символа а, если такое есть.Например: bababb -> babaabb
Задания:
написать алгоритм
протестировать с помощью эмулятора на слове bababb и на слове bb
Слайд 35Задание 8(перенос символа через слово)
А={a,b}.
Перенести в конец непустого слова Р его первый символ.
Пустое слово не менять.Например: bbaba -> babab
Задания:
написать алгоритм
протестировать с помощью эмулятора на слове baba и на входном слове из одного символа
Слайд 36Задание 9(использование нескольких спецзнаков)
А={а,b}
Удвоить
слово Р. т.е. приписать к P (слева или справа) его
копию.Например: abb -> abbabb
Задания:
написать алгоритм
протестировать с помощью эмулятора на двух входных словах - на пустом и на аbb.