Лекция 6

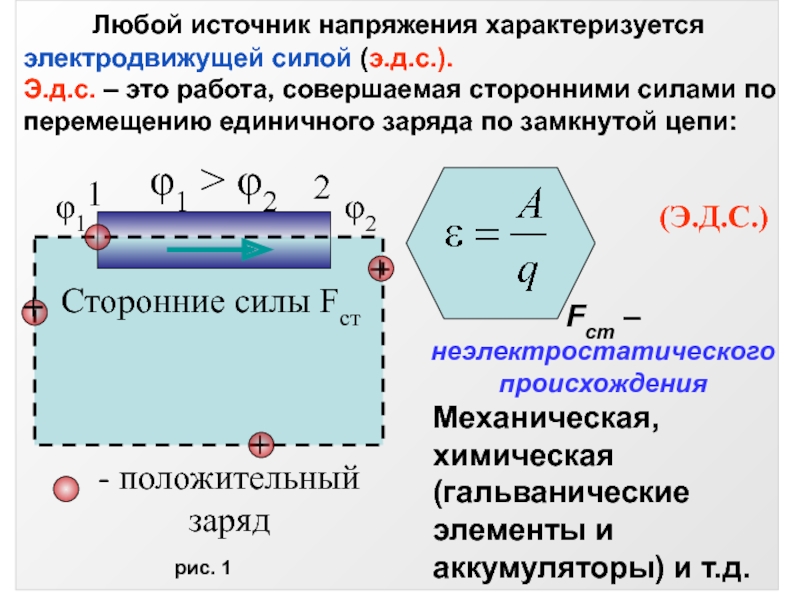
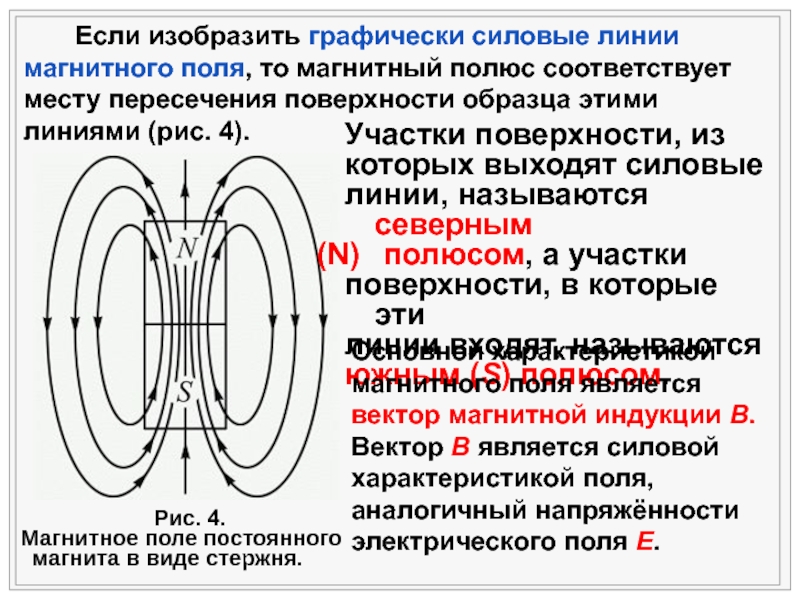
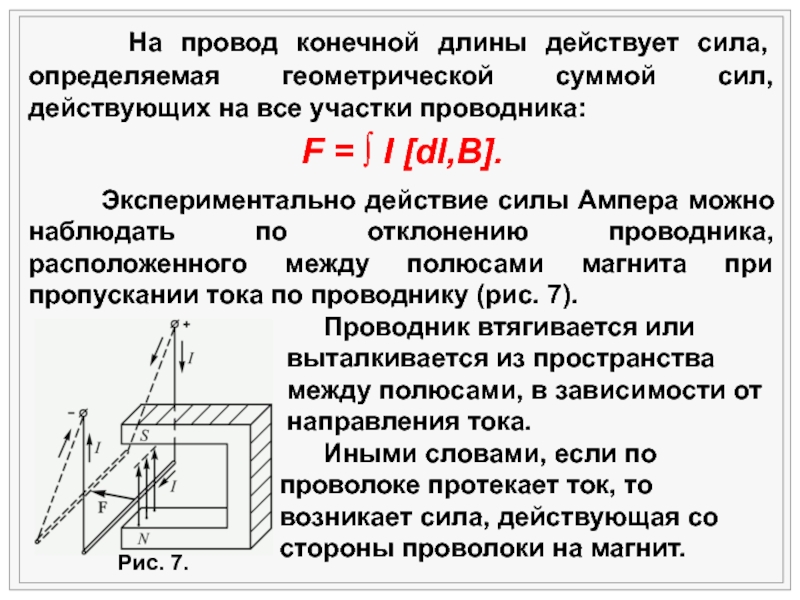
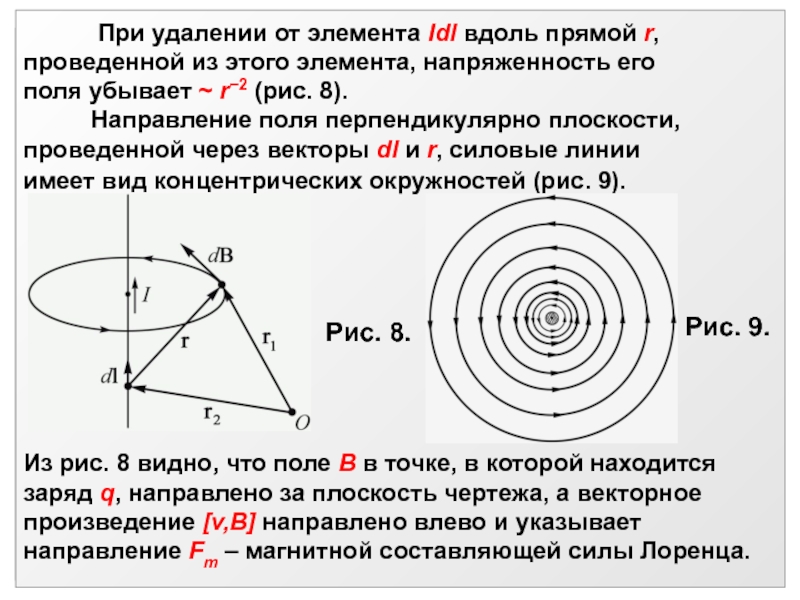
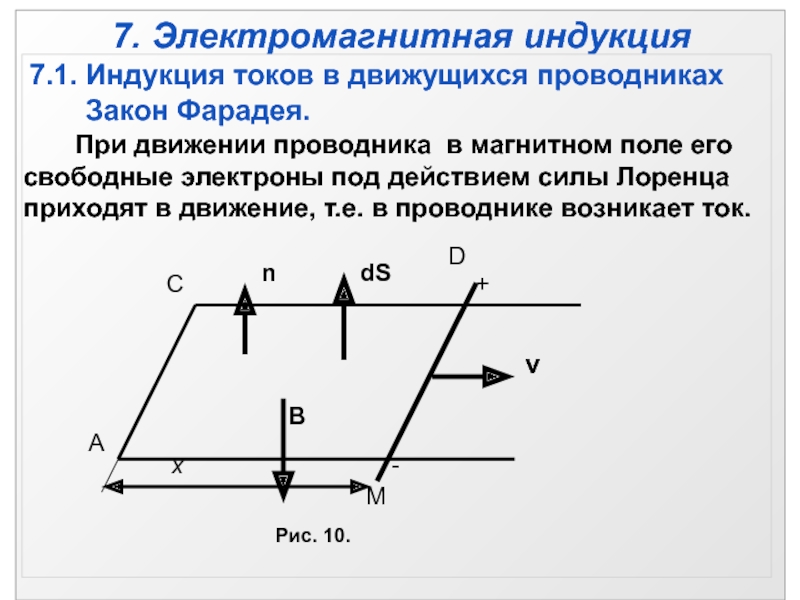
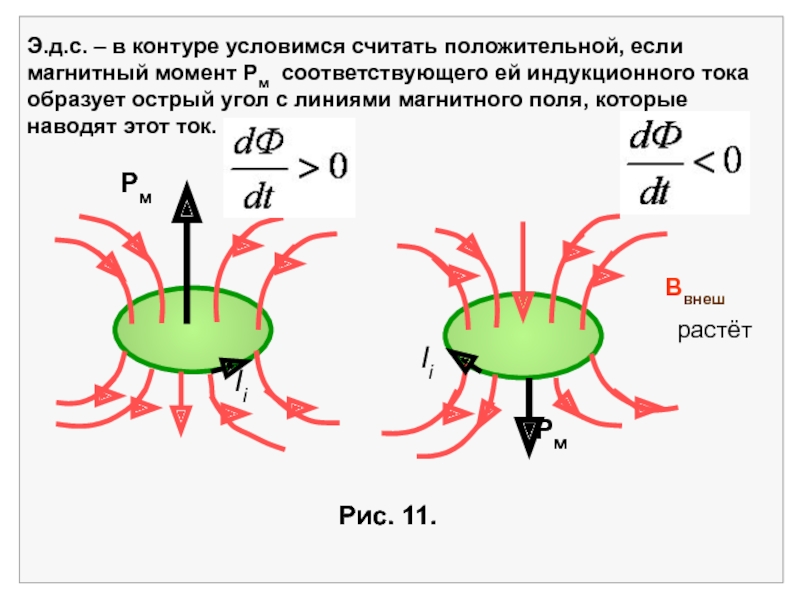
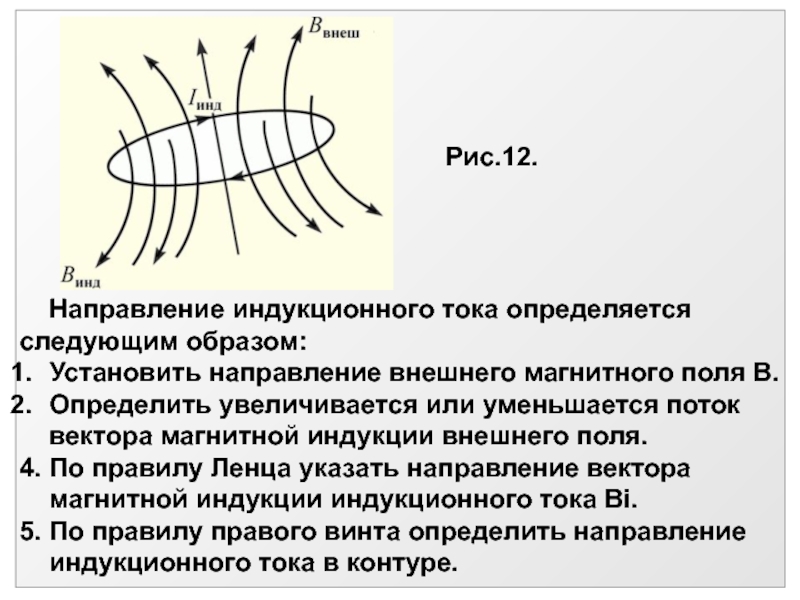
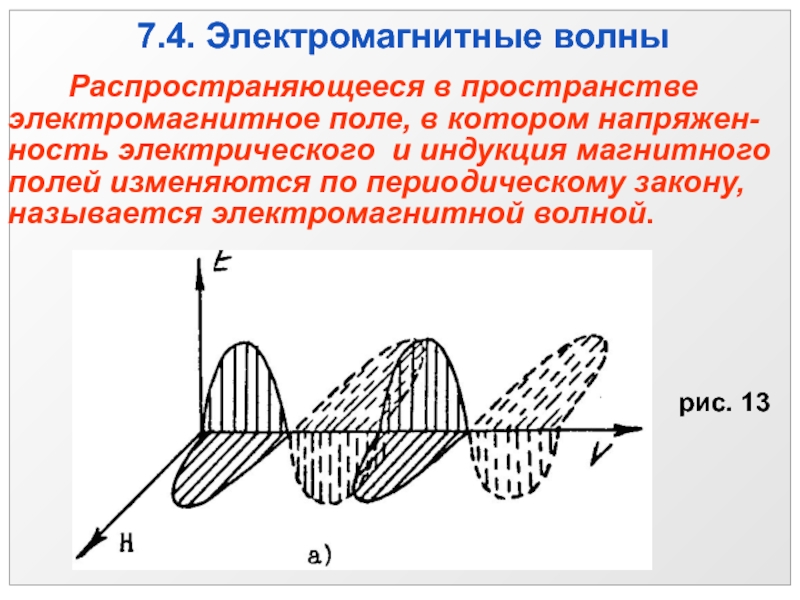
характеристики
5.1. Условия возникновения электрического тока
Сегодня:
Романовский Олег Анатольевич

Любое упорядоченное движение заряженных частиц называется электрическим током.
Для того, чтобы возник электрический ток необходимо выполнить следующие условия:
1) Наличие свободных заряженных частиц (в проводниках - свободные электроны, в жидкостях- положительные и отрицательные ионы).
2) Наличие постоянной разности потенциалов, которая может поддерживаться источником напряжения.

(э.д.с.).
Э.д.с. – это работа, совершаемая сторонними силами по перемещению

единичного заряда по замкнутой цепи:

+

+

φ1

φ2

φ1 > φ2

Сторонние силы Fст

+

1

2

- положительный заряд

Fст – неэлектростатического происхождения

(Э.Д.С.)

Механическая, химическая (гальванические элементы и аккумуляторы) и т.д.

рис. 1

тока.
Сила тока – это физическая величина численно равная количеству заряда,

протекающего через поперечное сечение проводника в единицу времени.
Для постоянного тока это можно записать следующим выражением


Плотностью тока мы называем векторную величину, равную количеству заряда, протекающего в единицу времени через единицу поперечного сечения проводника:

участка цепи.
,где ρ – удельное сопротивление
- удельная электропроводность
Закон Ома для

полной цепи

r - внутреннее сопротивление источника тока

трубки тока (рис. 2) длины dl и два близ-
ких ее

сечения. Обозначим потенциалы этих се-
чений через и , а величину площади сече-
ния через dS.
Применяя к выделенной трубке тока закон
Ома для однородного участка цепи, получим





разделив это выражение на dS,
получим с учетом

рис. 2

5.3. Закон Ома в дифференциальной форме

величины, характеризующие электрическое
состояние среды в одной и той же

точки.

Но так как напряженность и потенциал связаны как

получим, что

работу.
Работа тока затрачивается на увеличение внутренней энергии проводника, в

результате чего проводник нагревается. Принято говорить, что при протекании тока в
проводнике выделяется тепло dQ.
Если выделить участок проводника (рис. 2), то

5.4. Тепловое действие электрического тока.
Закон Джоуля-Ленца

Но следуя закону Ома для участка цепи, можно записать,
что U=IR. Тогда это выражение перепишется как

и dt, получим
количество тепла, выделяющееся в единице
объема

в единицу времени:

Величину  называют удельной тепловой
мощностью тока. Формула (выше) представляет
собой дифференциальную форму закона
Джоуля –Ленца.
Закон Джоуля –Ленца можно еще представить
в следующей форме:

токов и тел – магнетизм, осуществляе-
мый посредством магнитного поля. Термин

вве-
ден в 1845 г. М. Фарадеем.
Взаимодействие токов обусловлено наличием
особого вида материи, связанного с током,
которое называют магнитным полем.
Оно обладает непрерывным распределением
в пространстве и может занимать области, в ко-
торых уже существует вещество и другие поля
т.е. обладает свойством проницаемости.

6. Электромагнетизм
6.1 Источники магнитного поля. Силовые линии

токи.
Движение электронов и протонов создают орбитальные микротоки в

атомах и ядрах. Электроны и протоны обра-зуют атомные ядра, атомы, молекулы и все макротела, поэтому все вещества обладают магнитными свойствами
и подвержены влиянию магнитного поля.
Все вещества являются магнетиками.

Результаты исследования магнетизма
в эпоху Возрождения обобщены
Гильбертом (1600 г).
Он показал, что Земля – магнитный
диполь, и доказал невозможность
разъединения двух разноименных
магнитных полюсов.

Рис. 3. Направление силовых линий магнитного поля Земли

Рис. 4.
Магнитное поле постоянного
магнита в

виде стержня.

Участки поверхности, из
которых выходят силовые
линии, называются северным
полюсом, а участки
поверхности, в которые эти
линии входят, называются
южным (S) полюсом.

Основной характеристикой магнитного поля является вектор магнитной индукции B.
Вектор В является силовой характеристикой поля, аналогичный напряжённости
электрического поля Е.

устанавливается по касатель-
ной к окружности, очерченной вокруг проводника
с током

(рис.5а)
Иными словами, силовые линии магнитного
проводника с током имеют вид окружностей, в
центре которых находится проводник с током.

Для определения силовых линий маг-
нитного проводника с током служит
правило правой руки: проводник мыс-
ленно охватывается правой рукой так,
чтобы большой палец располагался в
направлении тока (положительных
зарядов); тогда остальные пальцы
загибаются в направлении силовых
линий (рис. 5б)

рис. 5б

рис.5а

Рассмотрим проводник с током, размещенный в магнитном поле.

Ток представляет совокупность зарядов q, двигающихся направленно со скоростью v. Концентрация зарядов равна n. Плотность тока при этом равна:
j = qvn.
Рассмотрим тонкий проводник площадью поперечного сечения S, длиной dl, объемом dV = Sdl.
В этом случае
dF = [j,B]dlS = [jSdl,B]
Или
dF = dV[j,B] = I[dl,B].
Размерность: [В] = H /A м = Тл (тесла)

На основе опытов по действию тока на магнит-ную стрелку

Эрстед пришел к заключению, что это воздействие связано с возникновением в простран-стве вокруг проводника с током магнитного поля.
Причиной появления магнитного поля являют-ся в конечном итоге движущиеся заряды.
Экспериментально действие элемента тока на магнитный полюс было изучено Био и Саваром.
Лаплас облек закон Био – Савара в математическую
форму. Закон, определяющий индукцию магнитного
поля dB элементарного отрезка тока Idl на расстоянии r
от него, называют законом Био – Савара – Лапласа:

где 0 = 4107 Гн/м =
=1,25663706144106 Гн/м (СИ) –
магнитная постоянная

на проводники с
током, но и на отдельные движущиеся частицы.

Силу, действующую на заряженную частицу,
движущуюся в магнитном поле, называют
силой Лоренца.
Сила, которую испытывает элемент тока в магнитном
поле – это результирующая всех сил, действующих на
отдельные заряды, движущиеся в этом элементе:

Силу тока можно представить как количество заряда,
протекающего в единицу времени через поперечное
сечение проводника I = q0nSdl, где q0 - величина заряда
отдельной частицы, n-число частиц в единице объема.

единицу времени, тогда
dt - равно единице. Поэтому dF =

q0nS dl B sin. S dl = V –
объем элемента тока, nV = N – число носителей заряда:

dF = q0vBN sin 

Тогда сила, действующая на отдельный заряд,
движущийся в магнитном поле равна:

Чаще под силой Лоренца понимают силу, действующую
на заряженную частицу одновременно со стороны двух
полей: электростатического и магнитного, тогда

Закон Фарадея.
При движении проводника в

магнитном поле его
свободные электроны под действием силы Лоренца
приходят в движение, т.е. в проводнике возникает ток.

Рис. 10.

что создаваемый им
магнитный поток сквозь поверхность,
ограниченную контуром, уменьшает

те
изменения магнитного потока, которые вызвали
появление индукционного тока.

внешнего магнитного поля В.
Определить увеличивается или уменьшается поток

вектора магнитной индукции внешнего поля.
4. По правилу Ленца указать направление вектора
магнитной индукции индукционного тока Вi.
5. По правилу правого винта определить направление
индукционного тока в контуре.

Рис.12.

случай явления электромагнитной индукции.      Из выражения (1) определяется единица

индуктивности – генри (Гн): 1 Гн – индуктивность такого контура, магнитный поток которого при силе тока 1 А равен 1 Вб:
1 Гн = 1 Вб/А.
     Индуктивность контура зависит от его геометрической формы, размеров и от магнитных свойств среды, в которой он находится. Например, для катушки (соленоида) длиной l и площадью сечения витка S, намотанной на сердечник с магнитной проницаемостью ,
(2)
          
  где N – общее число витков соленоида,   - магнитная постоянная.

электромагнитное поле, в котором напряжен-
ность электрического и индукция магнитного
полей

изменяются по периодическому закону,
называется электромагнитной волной.

во взаимно перпен-дикулярных плоскостях (рис.13). Одна синусоида отра-жает колебания вектора

напряженности электрического поля, другая - вектора индукции магнитного поля. Вектор скорости распространения электромагнитной волны будет перпендикулярен векторам и .

E = E0 sin (t - ) = E0 sin (t - )

B = B0 sin (t - ) = B0 sin (t - )

Эти формулы выражают закон изменения
электрического и магнитного полей в электро-
магнитной волне, распространяющейся в
направлении х.
Они называются уравнением электромагнитной
волны, где с- скорость распространения
электромагнитной волны в вакууме.