Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 6. Пересечение геометрических объектов общего положения
Содержание
- 1. Лекция 6. Пересечение геометрических объектов общего положения
- 2. 1. Алгоритм способа вспомогательных секущих поверхностей1. Построить
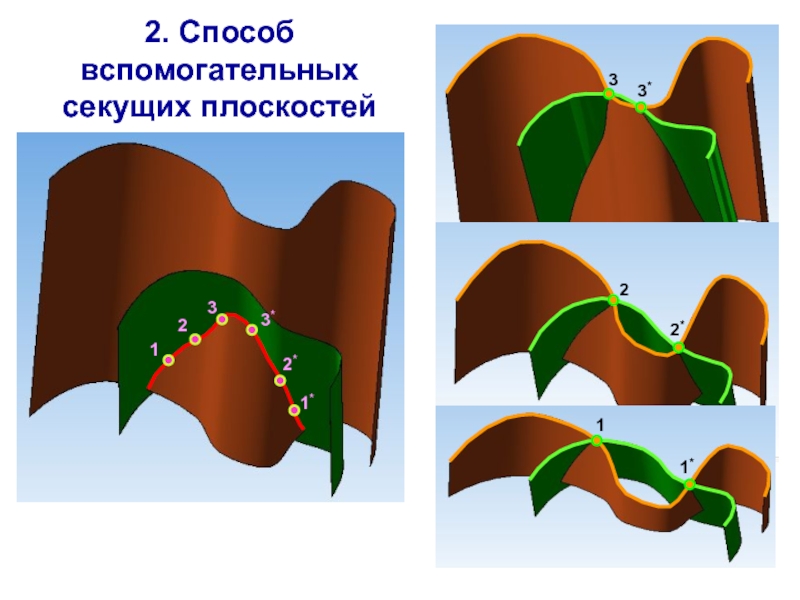
- 3. 2. Способ вспомогательных секущих плоскостей122*1*3*3122*1*3*3
- 4. Пересечение прямой общего положения с геометрическими объектами общего положенияПрямая и плоскостьПрямая и многогранникА212М2М1С2В222(32)=41=(51)А1С1В11121314252S2М2М1N1(N2)S1А212С2В2(22)А1С1В111213132
- 5. Слайд 5
- 6. Слайд 6
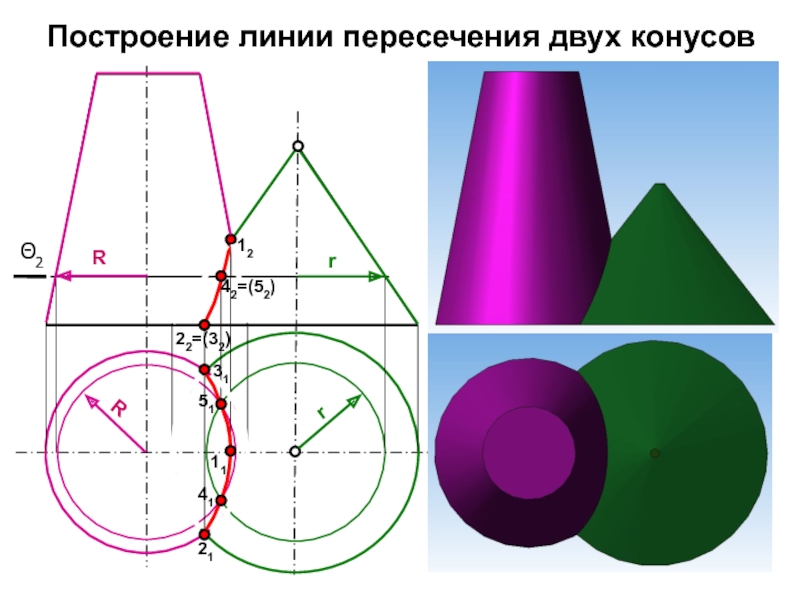
- 7. Построение линии пересечения двух конусовΘ21242=(52)22=(32)1121314151RRrr
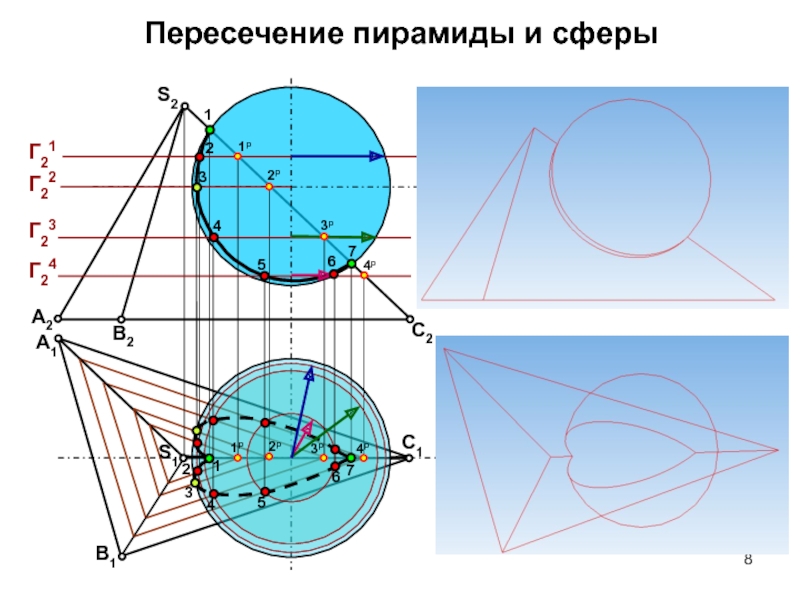
- 8. Пересечение пирамиды и сферыГ21А2В2С2S2А1В1С1S1123456712345671р2р3р4р1р2р3р4рГ22Г23Г24
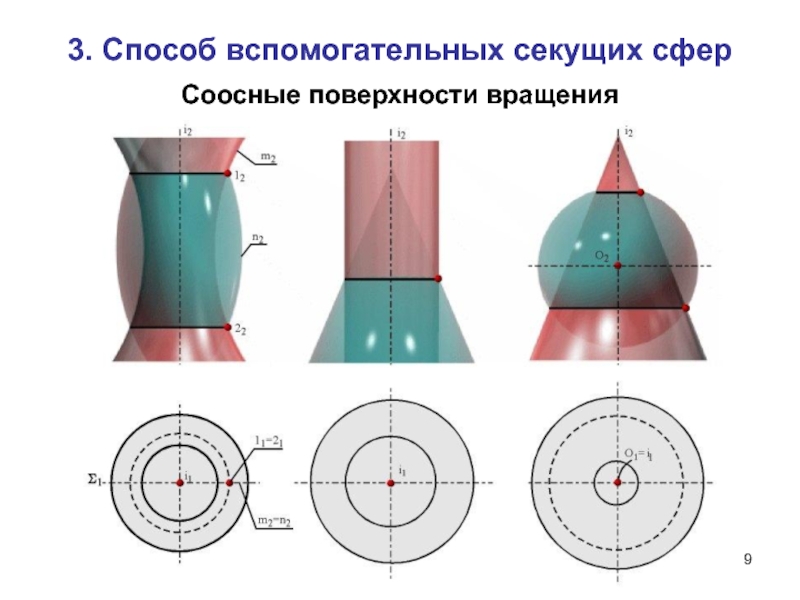
- 9. Соосные поверхности вращения3. Способ вспомогательных секущих сфер
- 10. Пересечение сферы поверхностями вращенияЛиния пересечения поверхностей вращения
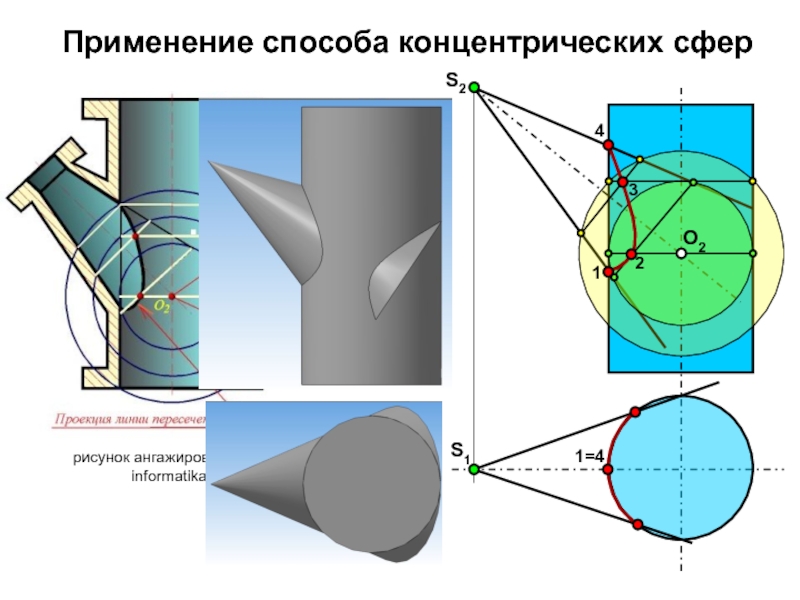
- 11. рисунок ангажирован с сайта informatika.ruПрименение способа концентрических сфер S2S1О212341=4
- 12. 4. Теорема МонжаЕсли две поверхности второго порядка
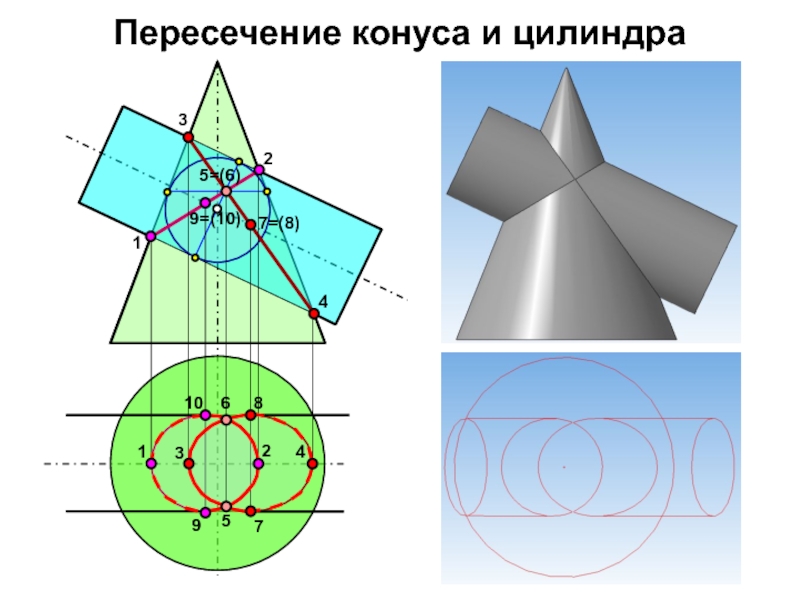
- 13. Пересечение конуса и цилиндра12345=(6)9=(10)7=(8)12345610798
- 14. Спасибо за внимание!
- 15. Скачать презентанцию
1. Алгоритм способа вспомогательных секущих поверхностей1. Построить вспомогательную поверхность, чтобы она пересекла обе заданные.2. Построить линию её пересечения с первой заданной поверхностью.3. Построить линию её пересечения со второй заданной поверхностью.4. Найти
Слайды и текст этой презентации
Слайд 1Лекция 6.
Пересечение геометрических объектов общего положения
Общий алгоритм способа вспомогательных
секущих поверхностей.
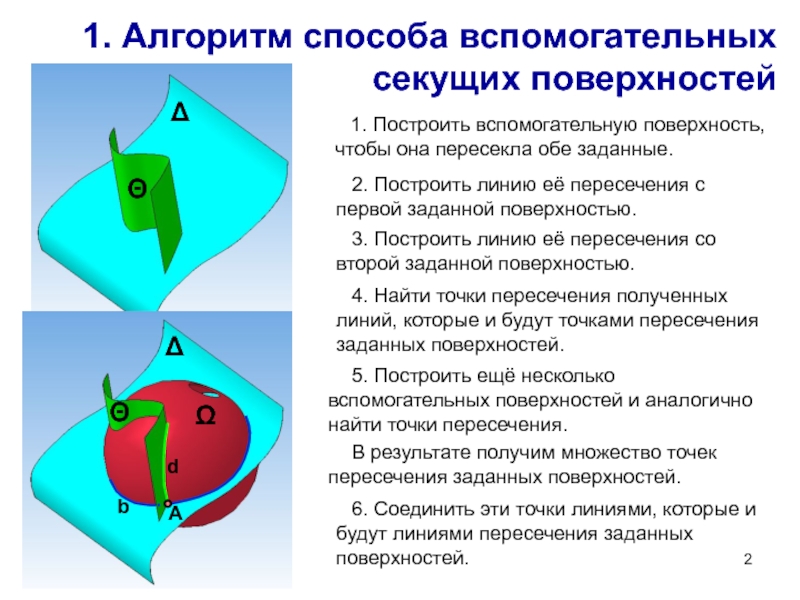
Слайд 21. Алгоритм способа вспомогательных секущих поверхностей
1. Построить вспомогательную поверхность, чтобы
она пересекла обе заданные.
2. Построить линию её пересечения с первой
заданной поверхностью.3. Построить линию её пересечения со второй заданной поверхностью.
4. Найти точки пересечения полученных линий, которые и будут точками пересечения заданных поверхностей.
5. Построить ещё несколько вспомогательных поверхностей и аналогично найти точки пересечения.
В результате получим множество точек пересечения заданных поверхностей.
6. Соединить эти точки линиями, которые и будут линиями пересечения заданных поверхностей.
Δ
Ω
Θ
Δ
Θ
d
A
b
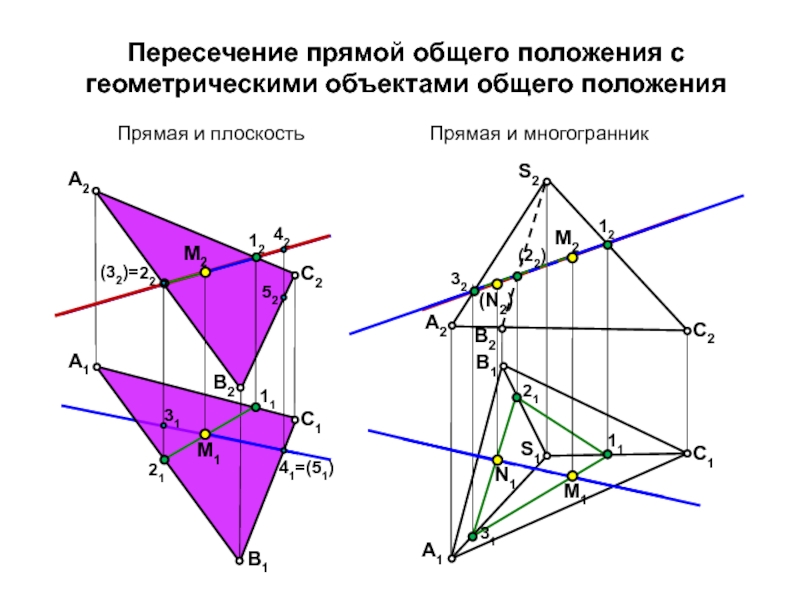
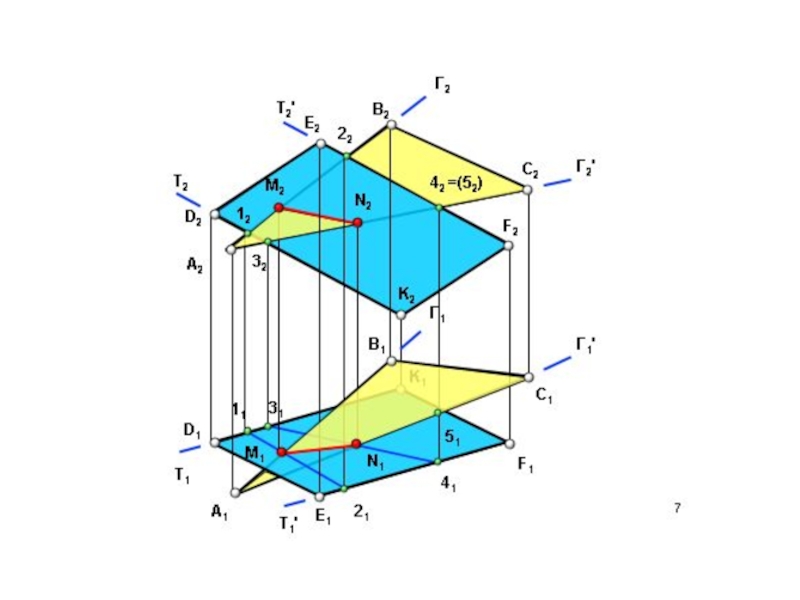
Слайд 4Пересечение прямой общего положения с геометрическими объектами общего положения
Прямая и
плоскость
Прямая и многогранник
А2
12
М2
М1
С2
В2
22
(32)=
41=(51)
А1
С1
В1
11
21
31
42
52
S2
М2
М1
N1
(N2)
S1
А2
12
С2
В2
(22)
А1
С1
В1
11
21
31
32
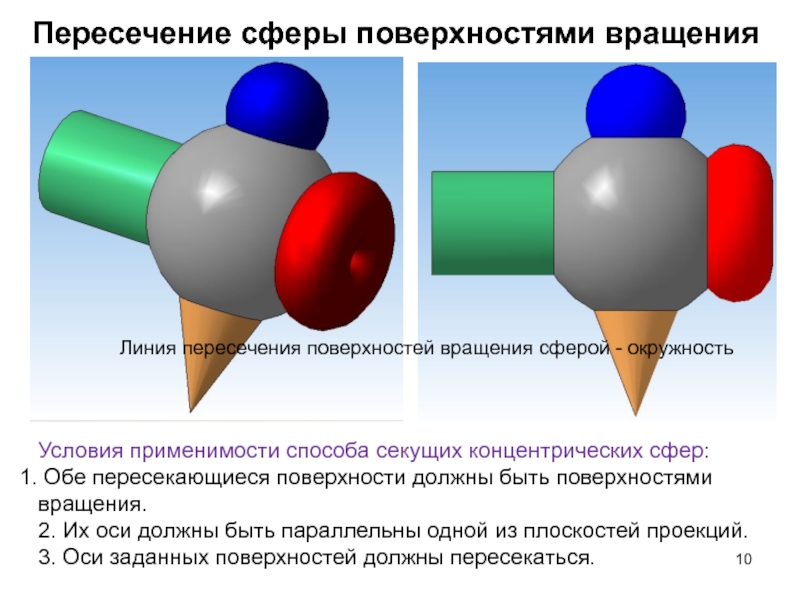
Слайд 10Пересечение сферы поверхностями вращения
Линия пересечения поверхностей вращения сферой - окружность
Условия
применимости способа секущих концентрических сфер:
Обе пересекающиеся поверхности должны быть
поверхностями вращения.2. Их оси должны быть параллельны одной из плоскостей проекций.
3. Оси заданных поверхностей должны пересекаться.
Слайд 11рисунок ангажирован с сайта informatika.ru
Применение способа концентрических сфер
S2
S1
О2
1
2
3
4
1=4
Слайд 124. Теорема Монжа
Если две поверхности второго порядка описаны около третьей
поверхности (или вписаны в неё), то линия их пересечения распадается
на две кривые второго порядка (эллипс, окружность, гиперболу, параболу). Причём плоскости этих кривых проходят через прямую, соединяющую точки пересечения линии касания.
