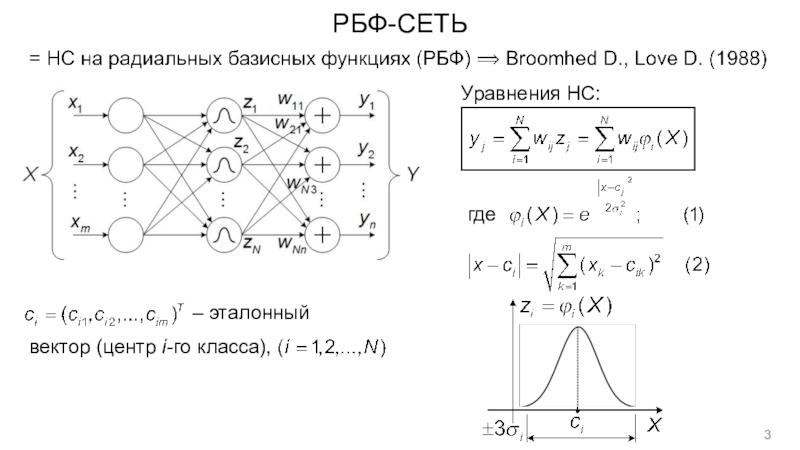
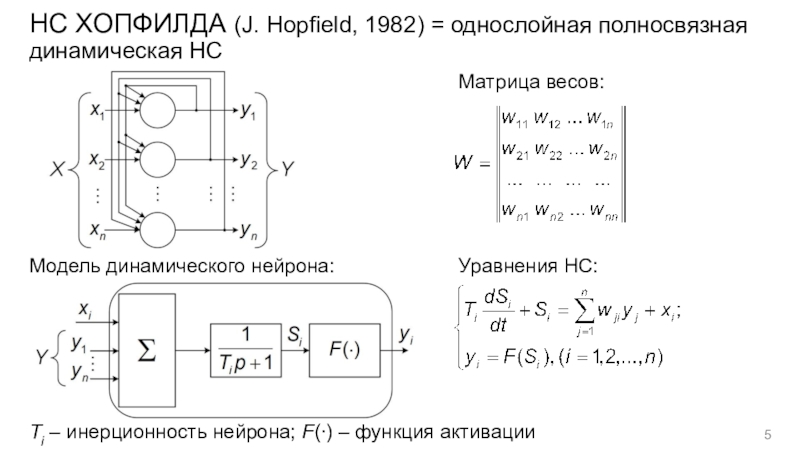
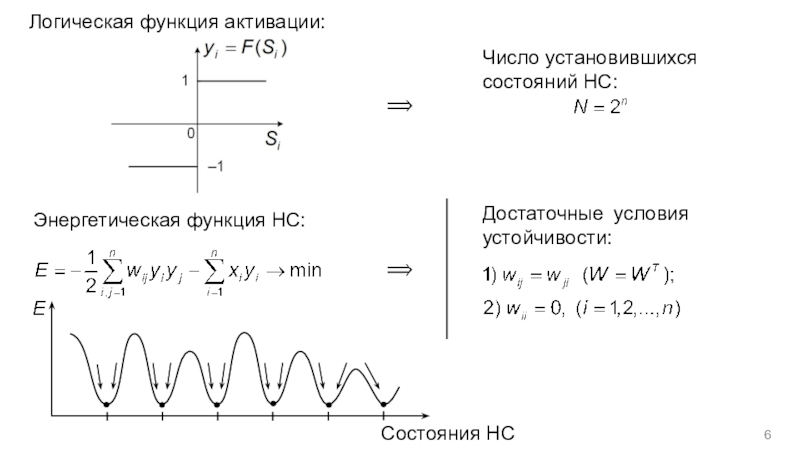
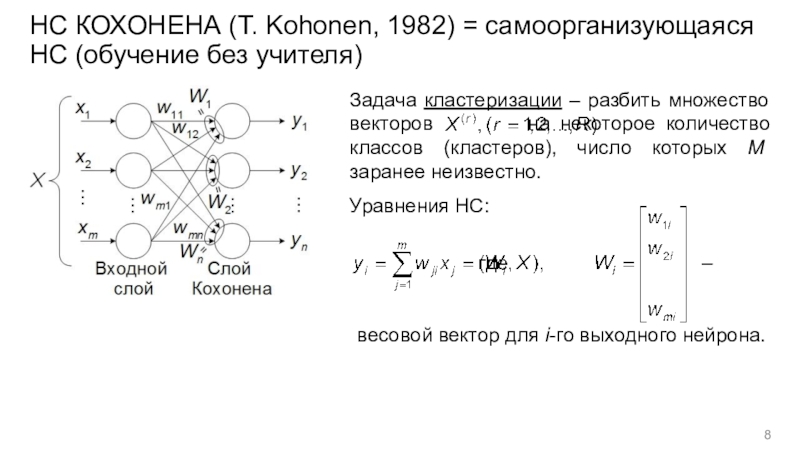
m переменных можно получить с помощью операций сложения, умножения и
суперпозиции из непрерывных функций одного переменного:Теорема (Cybenko G., Funahashi K., Hornik K.M. и др. 1989): любую непрерывную функцию m переменных можно с любой степенью точности реализовать с помощью персептрона с одним скрытым слоем, имеющего достаточное количество нейронов в скрытом слое.
X
Y