Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 9
Содержание
- 1. Лекция 9
- 2. Два типа грамматикРаспознающая грамматикаПорождающая грамматика
- 3. Этапы распознаванияНа первом этапе определяется грамматика –
- 4. Этапы распознаванияНа второй этапе принимается решение о
- 5. Порождение языкаЗадаются правила, механизм порождения слов языка
- 6. Определение: Конечным автоматом-распознавателем называется пятерка объектов:
- 7. Определение: Конечный автомат-распознаватель A= допускает входную цепочку
- 8. Определение Язык, для которого существует распознающий его конечный автомат, называют автоматным языком.
- 9. Примеры языков 1. V = {a, b, c} ; L = {abc, aa}
- 10. Полный граф автоматного языка
- 11. Примеры2. V2 = {а, b с}; L2
- 12. Примеры3. V4 = {а, b, с}; L4
- 13. Примеры4. V3 = {a,b,c};L3 = V3*. Автомат с
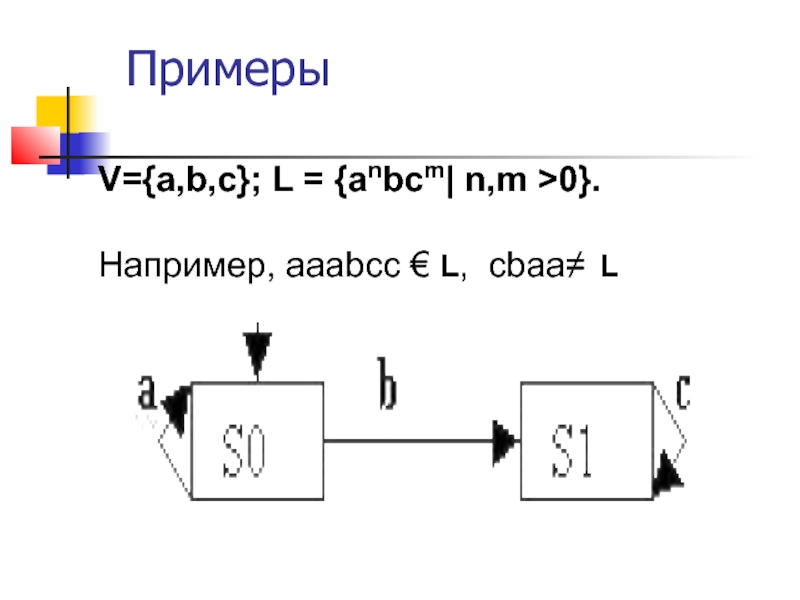
- 14. ПримерыV={a,b,c}; L = {anbcm| n,m >0}. Например, aaabcc € L, cbaa≠ L
- 15. ПримерыV = {+,-,0,…,9}; L ={множество целых числовых констант}
- 16. ПримерыV={+,-,0,…,9,'.'}; L = {множество вещественных чисел}
- 17. УтверждениеЛюбой автоматный язык задается синтаксической диаграммой и
- 18. Недетерминированный автоматАвтомат, у которого допускается неоднозначный переход
- 19. Пример недетерминированного автомата
- 20. Операции над языкамиТеорема 1. Объединение и пересечение
- 21. ОпределениеПроизведением двух языков называется множество слов, полученных
- 22. ОпределениеПусть _ - пустое слово, L –
- 23. Теорема КлиниЯзык, полученный конечным набором распознаваемых языков
- 24. Анализ предложенийРассмотрим предложение, состоящее из подлежащего и
- 25. Анализ предложенийПусть дано предложение «Дождь идет» <
- 26. Пример Грамматика: S::=хА,правило подстановки A::=zyA. Проверить является
- 27. Ограничение 1Если А::=12....n порождаемое правило, где i
- 28. ПримерВ грамматике S::=АВ;A::=хАy;В::=хBzНарушено ограничение 1, т.к. определение нетерминальных символов А и В начинается с символа х.
- 29. Ограничение 2Для любого нетерминального символа А, который
- 30. ПримерРассмотрим грамматику: S::=Ax; A::=x _, ограничение 2 нарушено, так как first(A) follow(А)={x}.
- 31. ОграничениеБудем рассматривать грамматические системы, которые удовлетворяют вышеназванным ограничениям
- 32. Примеры грамматикЯзыки программированияАлгоритмический языкСинтаксис и семантика текстовых редакторов (Word)Переводчики
- 33. Формальный исполнитель алгоритма - субъект или устройство,
- 34. Формальный исполнительИсполнитель алгоритма считается заданным, если для
- 35. Контроль алгоритмаПричинами невыполнения алгоритма могут быть:ошибки синтаксиса;выход
- 36. Настоящее и будущееКомпьютер через свое программное обеспечение
- 37. Контрольные вопросы1. Приведите примеры порождающей и распознающей
- 38. Скачать презентанцию
Два типа грамматикРаспознающая грамматикаПорождающая грамматика
Слайды и текст этой презентации
Слайд 3Этапы распознавания
На первом этапе определяется грамматика – правила, которым подчиняются
конструкции образов (в смысле термина, используемого в лингвистике).
Слайд 4Этапы распознавания
На второй этапе принимается решение о том, принадлежит ли
предъявленный объект к множеству всех объектов, порождаемых заданной грамматикой.
Слайд 6Определение:
Конечным автоматом-распознавателем называется пятерка объектов:
A =
s0, d, F>, где:
S - конечное непустое множество (состояний);
X -
конечное непустое множество входных сигналов (входной алфавит);s0 S - начальное состояние;
d : SxX → S - функция переходов;
F - множество заключительных состояний
Слайд 7Определение:
Конечный автомат-распознаватель A= допускает входную
цепочку из Х*, если эта цепочка переводит его из начального
состояния в одно из заключительных состояний.Множество всех цепочек, допускаемых автоматом А, образует язык, допускаемый А.
Слайд 8Определение
Язык, для которого существует распознающий его конечный автомат, называют автоматным
языком.
Слайд 11Примеры
2. V2 = {а, b с}; L2 = «»
Любой автомат
с пустым множеством заключительных состояний допускает L2.
Слайд 13Примеры
4. V3 = {a,b,c};L3 = V3*.
Автомат с единственным состоянием, которое
является заключительным, имеющий три перехода из этого состояния в него
же, помеченные символами из VЗ, допускает L3
Слайд 17Утверждение
Любой автоматный язык задается синтаксической диаграммой и обратно, по любой
синтаксической диаграмме можно построить конечный автомат (в общем случае недетерминированный),
распознающий тот же язык, который задает синтаксическая диаграмма
Слайд 18Недетерминированный автомат
Автомат, у которого допускается неоднозначный переход к заданному состоянию,
либо распознаваемая цепочка символов может имеет не один маршрут к
заключительному состоянию, называют недетерминированным
Слайд 20Операции над языками
Теорема 1. Объединение и пересечение двух распознаваемых языков,
а также дополнение к распознаваемому языку является распознаваемым языком.
Следствие. Любой
язык, состоящий из конечного количества слов, является распознаваемым.
Слайд 21Определение
Произведением двух языков называется множество слов, полученных путем всевозможных произведений
слов первого языка на слова второго. При этом под произведением
двух слов понимается их склеивание (конкатенация).Теорема 2.
Произведение двух распознаваемых языков является распознаваемым.
Слайд 22Определение
Пусть _ - пустое слово, L – некоторый язык. Определим
степени языка: L0 = {_},
L1 = L, L n+1 =
LLn Множество L* = U Ln , полученное объединением всех Ln , называют итерацией языка L.
Теорема 3. Итерация распознаваемого языка является распознаваемым.
Слайд 23Теорема Клини
Язык, полученный конечным набором распознаваемых языков применением к ним
операций объединения, произведения и итерации является распознаваемым языком. И, обратно,
если язык распознаваем, то он получен из конечного набора языков применением к ним конечного числа операций объединения, умножения и итерации.
Слайд 24Анализ предложений
Рассмотрим предложение, состоящее из подлежащего и сказуемого.
Дождь - подлежащее;
идет - сказуемое.
Предложение в терминах Бекуса и Наура:
::=
::=дождь солнце
::=идетсветит.
Слайд 25Анализ предложений
Пусть дано предложение «Дождь идет»
< сказуемое> Дождь идет
Дождь
идет
Результат положительный, текст является
предложением 
Слайд 26Пример
Грамматика: S::=хА,
правило подстановки A::=zyA. Проверить является ли предложением xyyz?
Попытаемся сконструировать искомое предложение: S -> xA -> xyA ->
xyyA -> xyyz. Результат положительный.
Слайд 27Ограничение 1
Если А::=12....n порождаемое правило, где i - последовательность символов,
то множество начальных символов всех предложений, порождаемых из различных i
не должны пересекаться,т.е. First(i) First(j)=0, для всех i ≠ j.
First() - это множество всех терминальных символов, которые могут встречаться в начале предложений.
Слайд 28Пример
В грамматике
S::=АВ;
A::=хАy;
В::=хBz
Нарушено ограничение 1, т.к. определение нетерминальных символов А
и В начинается с символа х.
Слайд 29Ограничение 2
Для любого нетерминального символа А, который порождает пустую последовательность
(A_), множество начальных символов не должно пересекаться со множеством символов,
которые могут появляться в предложениях языка, порождаемой А, справа, то есть first(A) follow(А)=.
Слайд 30Пример
Рассмотрим грамматику:
S::=Ax; A::=x _,
ограничение 2 нарушено, так как
first(A) follow(А)={x}.
Слайд 31Ограничение
Будем рассматривать грамматические системы, которые удовлетворяют вышеназванным ограничениям
Слайд 32Примеры грамматик
Языки программирования
Алгоритмический язык
Синтаксис и семантика текстовых редакторов (Word)
Переводчики
Слайд 33Формальный исполнитель алгоритма
- субъект или устройство, способные воспринимать и
анализировать указания алгоритма, изменять в соответствии с ним свое состояние,
а также обладающие механизмом исполнения, способным производить пошаговую обработку информации
Слайд 34Формальный исполнитель
Исполнитель алгоритма считается заданным, если для него установлены:
- система
команд;
- формы представления входной и выходной информации;
- система допустимых внутренних
состояний;- язык представления алгоритма.
Слайд 35Контроль алгоритма
Причинами невыполнения алгоритма могут быть:
ошибки синтаксиса;
выход начальных данных за
пределы допустимого множества;
- несоответствие алгоритма возможностям исполнителя.
Слайд 36Настоящее и будущее
Компьютер через свое программное обеспечение предоставляет пользователю множество
исполнителей, из которых следует выбрать оптимальный, т.е. наиболее соответствующий задаче
и алгоритму.
Слайд 37Контрольные вопросы
1. Приведите примеры порождающей и распознающей грамматик.
2. Как выглядят
синтаксическая диаграмма и конечный автомат для условного оператора?
3. Пусть задана
грамматика S::=AB и правила подстановки A::=xAy, B::=xBz. Проверить, является ли заданный текст xxxz правильным предложением?
