Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция № 4
Содержание
- 1. Лекция № 4
- 2. 1. КонъюнкцияОбозначение: , (на выбор)Выражение в
- 3. 2. Нестрогая дизъюнкцияОбозначение: Выражение в естественном языке:
- 4. 3. Строгая дизъюнкцияОбозначение: Выражение в естественном языке:
- 5. 4. ИмпликацияОбозначение: Выражение в естественном языке: если
- 6. 5. ЭквиваленцияОбозначение: Выражение в естественном языке: если
- 7. 6. ОтрицаниеОбозначение: Выражение в естественном языке:
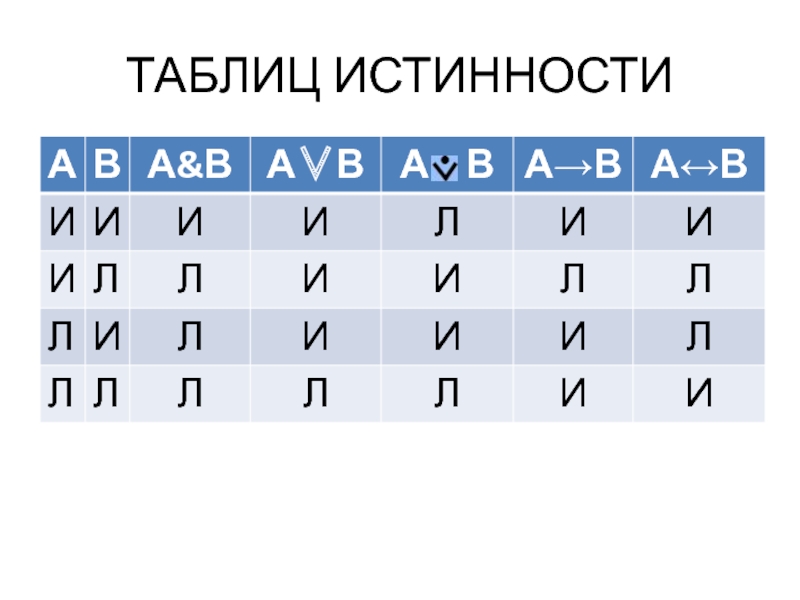
- 8. ТАБЛИЦ ИСТИННОСТИ
- 9. ТАБЛИЦ ИСТИННОСТИТаблица истинности — соответствие всех возможных
- 10. Виды сложных суждений (по таблицам истинности)ТАВТОЛОГИЯ
- 11. Пример № 1: Формализовать и проверить правильность
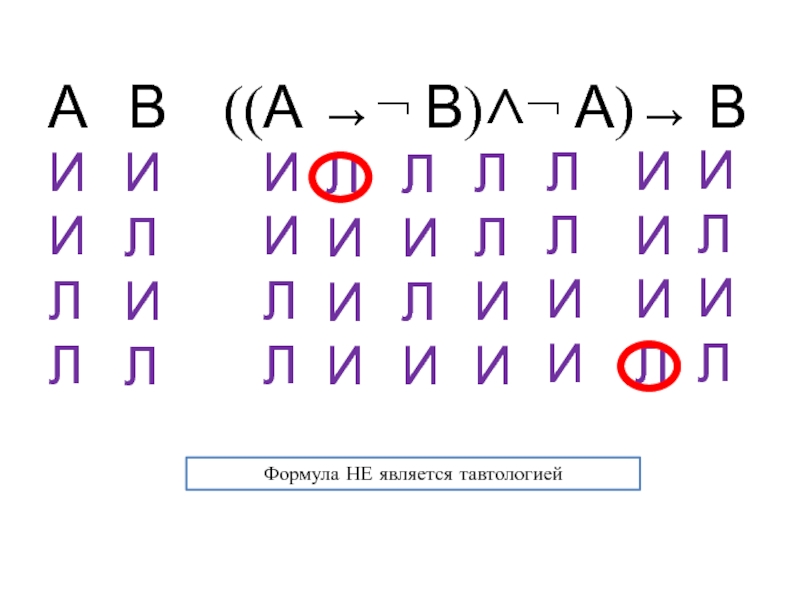
- 12. А В ((А В) А) ВИИЛЛИЛИЛИИЛЛЛЛИИИЛИЛЛИЛИЛИИИЛЛИИИИИЛФормула НЕ является тавтологией
- 13. Пример № 2: Формализовать и проверить правильность
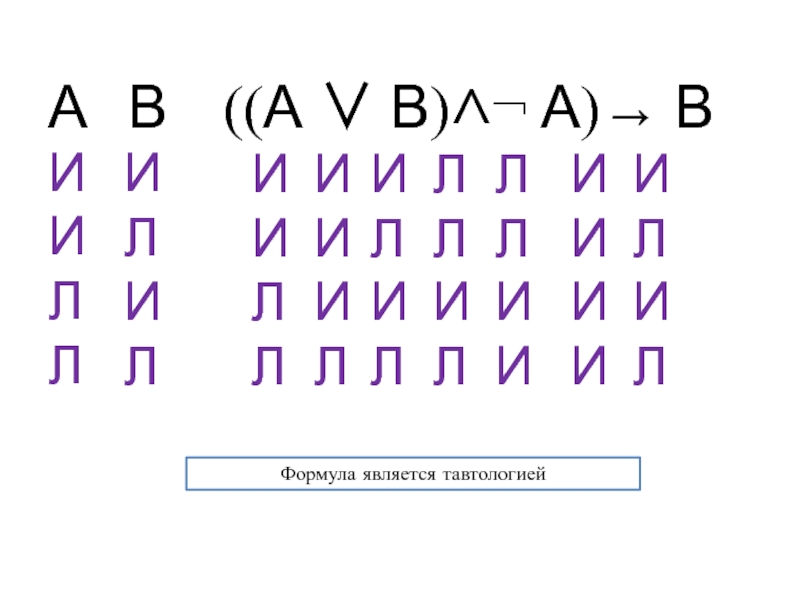
- 14. А В ((А В) А) ВИИЛЛИЛИЛИИЛЛЛЛИИИЛИЛИЛИЛИИИЛЛЛИЛИИИИФормула является тавтологией
- 15. Таблицы истинностиТЕКСТ: «Нация стремится к войне или
- 16. ИИИИЛЛЛЛИИЛЛИИЛЛИЛИЛИЛИЛИИИИЛЛЛЛИИИИЛЛЛЛИИЛЛИИЛЛИИЛЛИИЛЛИЛИЛИЛИЛИЛИЛИЛИЛЛЛЛЛИИИИЛИЛИЛИЛИИИИИИИЛЛИЛИЛИЛЛИЛЛЛЛИЛЛИИЛЛИИЛЛИИИИИИИИИПодставляем значенияУчитываем отрицанияПоследовательно вычисляем значенияФормула является тавтологией
- 17. Скачать презентанцию
1. КонъюнкцияОбозначение: , (на выбор)Выражение в естественном языке: и, а, но...Условия истинности: конъюнкция двух высказываний истинна, если только если истинны одновременно оба высказывания
Слайды и текст этой презентации
Слайд 21. Конъюнкция
Обозначение: , (на выбор)
Выражение в естественном языке: и,
а, но...
истинны одновременно оба высказывания
Слайд 32. Нестрогая дизъюнкция
Обозначение:
Выражение в естественном языке: или...
Условия истинности: нестрогая
дизъюнкция двух высказываний истинна, если и только если истинно хотя
бы одно высказывание
Слайд 43. Строгая дизъюнкция
Обозначение:
Выражение в естественном языке: либо, … либо
….
Условия истинности: строгая дизъюнкция двух высказываний истинна, если и только
если истинно в точности одно высказывание
Слайд 54. Импликация
Обозначение:
Выражение в естественном языке: если … то, следовательно,
значит
Условия истинности: импликация двух высказываний ложна, если только если условие
импликации — истинно, а заключение - ложно
Слайд 65. Эквиваленция
Обозначение:
Выражение в естественном языке: если и только если
Условия
истинности: эквиваленция двух высказываний истинна, если и только если они
оба одновременно либо истинны, либо ложны
Слайд 76. Отрицание
Обозначение:
Выражение в естественном языке: неверно, что
Условия истинности:
отрицание высказывания истинно если и только если само высказывание ложно
Слайд 9ТАБЛИЦ ИСТИННОСТИ
Таблица истинности — соответствие всех возможных наборов истинностных значений
простых суждений истинностным значениям сложного суждения
Количество строк
в таблице истинности
= 2 количество переменных
Слайд 10Виды сложных суждений
(по таблицам истинности)
ТАВТОЛОГИЯ (логический закон) — суждение,
истинное при любом наборе истинностных значений составляющих его простых суждений
ЛОГИЧЕСКОЕ
ПРОТИВОРЕЧИЕ - суждение, ложное при любом наборе истинностных значений составляющих его простых суждений
Слайд 11Пример № 1: Формализовать и проверить правильность рассуждения
Если формула ошибочна,
то результаты эксперимента не совпадут с расчетами. Формула, без сомнения,
корректна, значит, результаты эксперимента обязательно совпадут с расчетамиА - формула ошибочна
В - результаты эксперимента совпадут с расчетами
Слайд 13Пример № 2: Формализовать и проверить правильность рассуждения
Чарльз Доджсон может
быть известен вам как математик или детский писатель, но как
математик он вам не известен. Следовательно, он известен как детский писатель.А – Ч. Доджсон известен как математик
В - Ч. Доджсон известен как детский писатель
Слайд 15Таблицы истинности
ТЕКСТ: «Нация стремится к войне или коммерции тогда и
только тогда, когда потребности нации превосходят имеющиеся ресурсы.
Современные нации
не стремятся к войне. Значит, либо их потребности не превосходят имеющиеся ресурсы, либо же они стремятся к коммерции»
Переменные (простые суждения):
В – Нация стремится к войне
К – Нация стремится к коммерции
П - Потребности какой-либо нации превосходят имеющиеся ресурсы
ТЕКСТ С ПЕРЕМЕННЫМИ:
В или К тогда и только тогда, когда П.
не-В.
Значит, либо не-П, либо К»
Слайд 16И
И
И
И
Л
Л
Л
Л
И
И
Л
Л
И
И
Л
Л
И
Л
И
Л
И
Л
И
Л
И
И
И
И
Л
Л
Л
Л
И
И
И
И
Л
Л
Л
Л
И
И
Л
Л
И
И
Л
Л
И
И
Л
Л
И
И
Л
Л
И
Л
И
Л
И
Л
И
Л
И
Л
И
Л
И
Л
И
Л
Л
Л
Л
Л
И
И
И
И
Л
И
Л
И
Л
И
Л
И
И
И
И
И
И
И
Л
Л
И
Л
И
Л
И
Л
Л
И
Л
Л
Л
Л
И
Л
Л
И
И
Л
Л
И
И
Л
Л
И
И
И
И
И
И
И
И
И
Подставляем значения
Учитываем отрицания
Последовательно вычисляем значения
Формула является тавтологией
