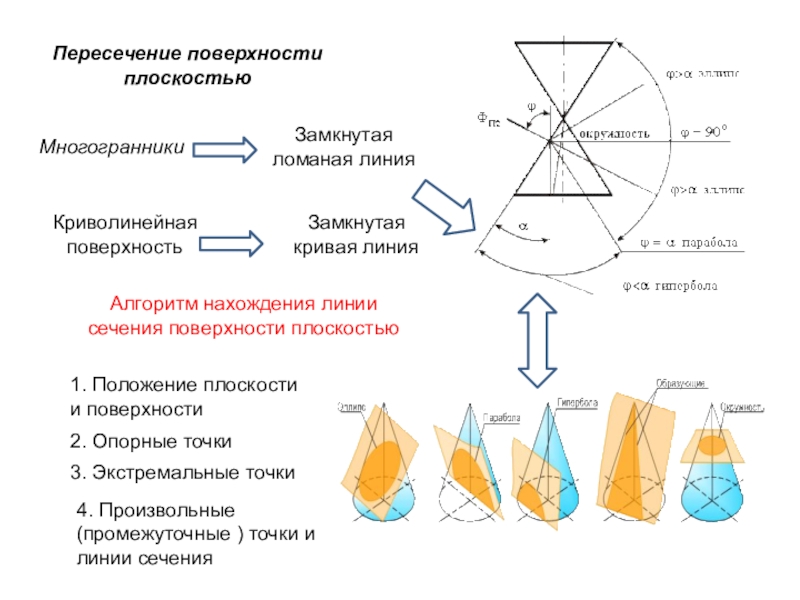
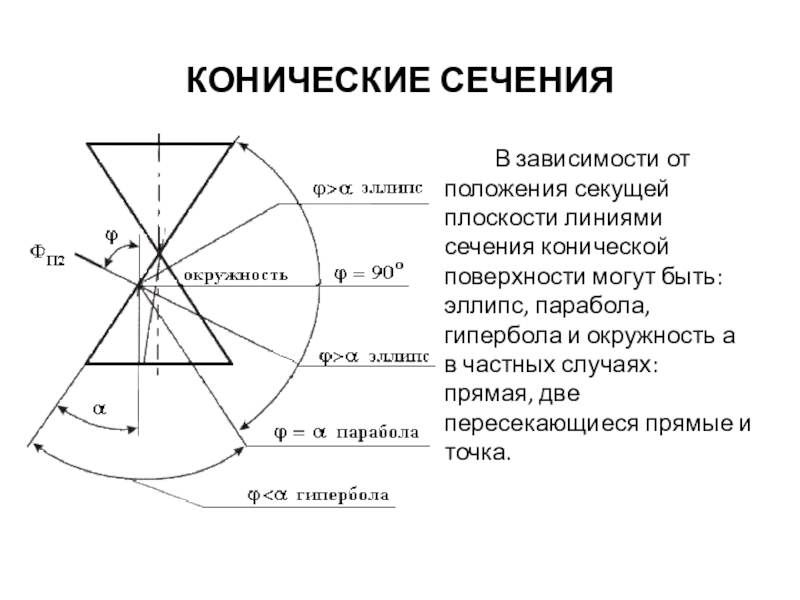
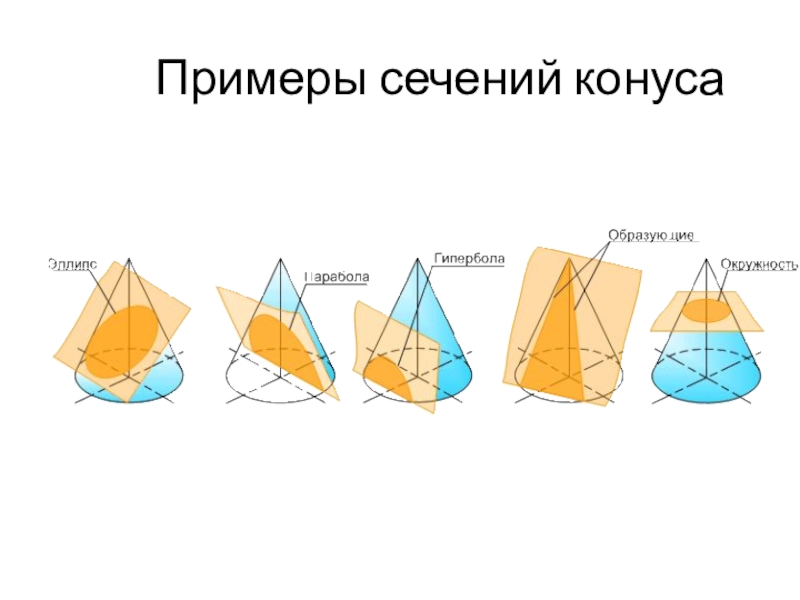
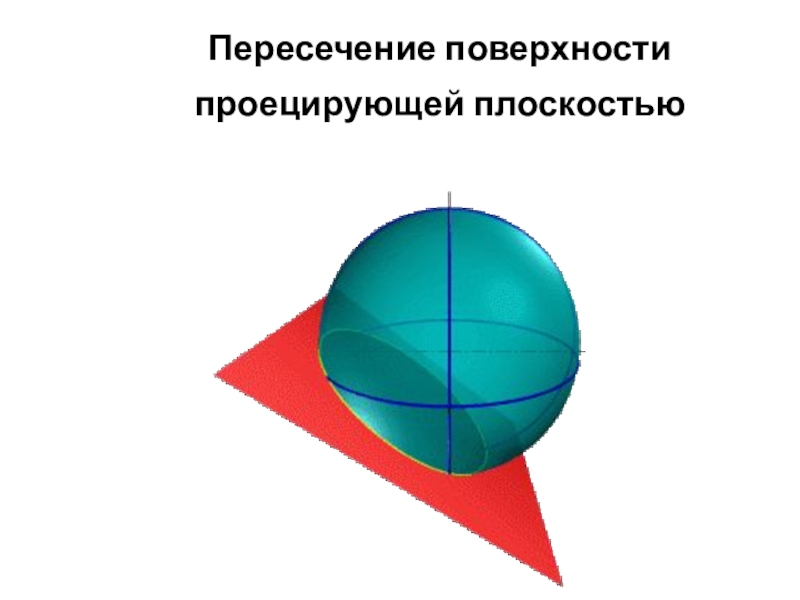
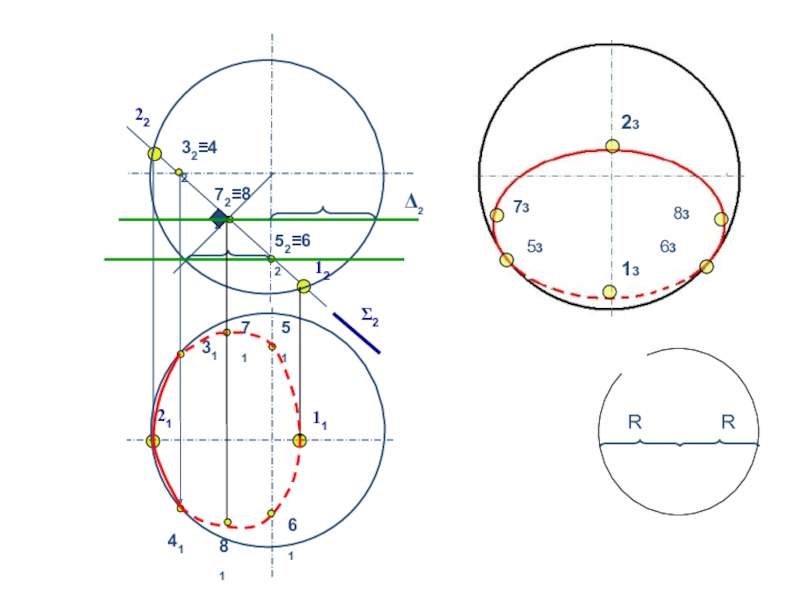
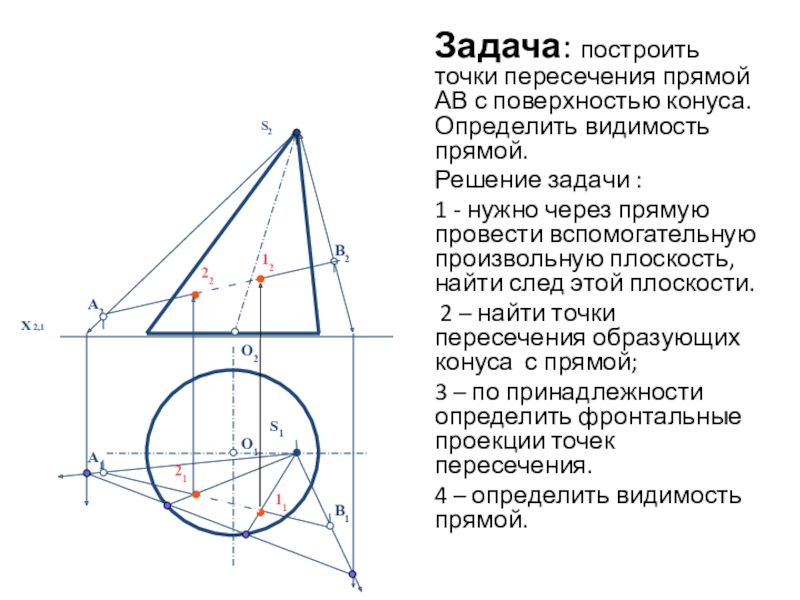
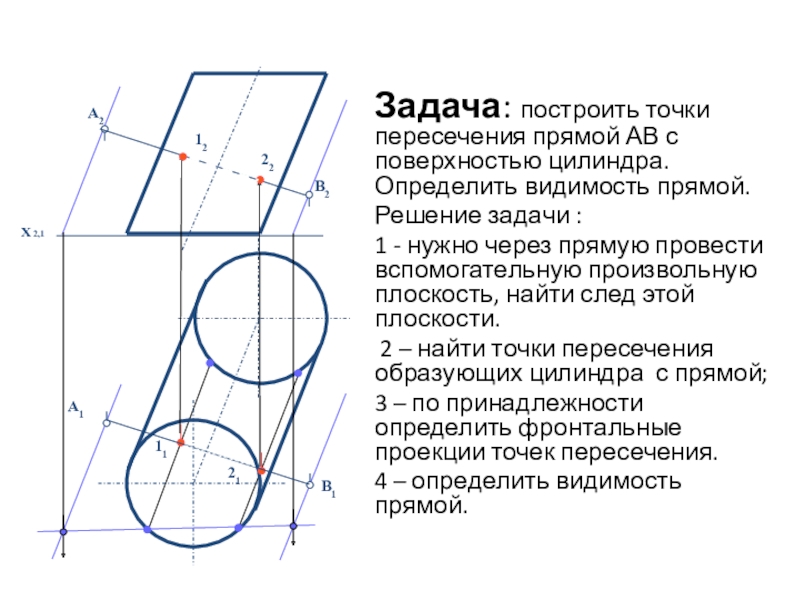
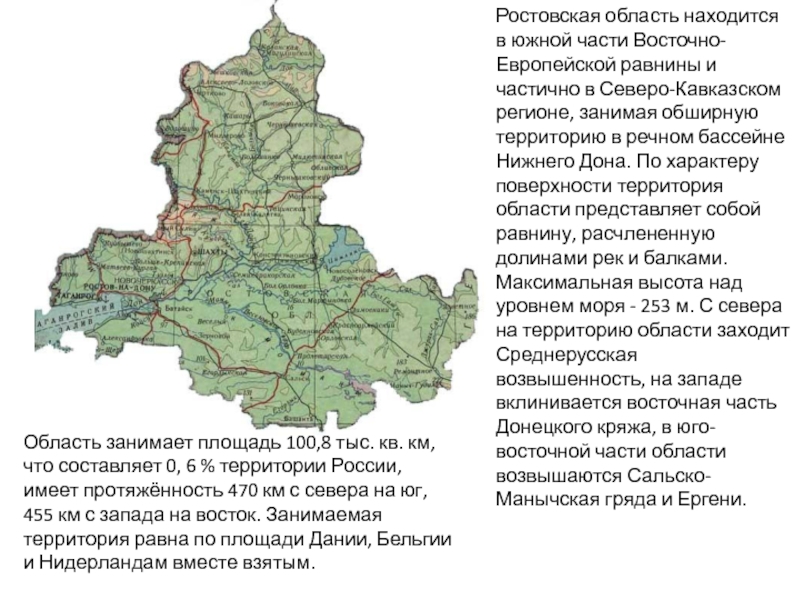
линии сечения поверхности плоскостью
2. Опорные точки
3. Экстремальные точки
1. Положение плоскости
и поверхности4. Произвольные (промежуточные ) точки и линии сечения