Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №1 Вектора Кинематика к.ф.-м.н., доцент ШЕН Стеблий Максим Евгеньевич г
Содержание
- 1. Лекция №1 Вектора Кинематика к.ф.-м.н., доцент ШЕН Стеблий Максим Евгеньевич г
- 2. ВведениеМатериальная точка – тело, размерами которого в
- 3. ВекторПредставление вектора:1) две точки2) радиус-вектор - вектор,
- 4. Операции над векторамиНахождение модуля – вычисление длиныПроекция вектора на осьУмножение на числоСложениеВычитание
- 5. Операции над векторамиСкалярное произведение векторов - операция
- 6. Скорость. Ускорение.r1r2ΔrΔSxyПоложение материальной точки в пространстве зададим
- 7. Скорость. Ускорение.Скорость – векторная физическая величина, характеризующая быстроту перемещения и
- 8. Выразим ускорение через известные величины R и
- 9. Ускорение при криволинейном движении 12034υυ+ΔυΔυnυ+ΔυΔSΔϕΔϕn’nRRτЕсли движение криволинейное
- 10. Вращение с постоянной угловой скоростью характеризуется временем
- 11. Связь поступательного и вращательного движенияВо вращающемся теле
- 12. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Лекция №1
Вектора
Кинематика
к.ф.-м.н., доцент ШЕН
Стеблий Максим Евгеньевич
г. Владивосток
2019
Курс общей физики
Слайд 2Введение
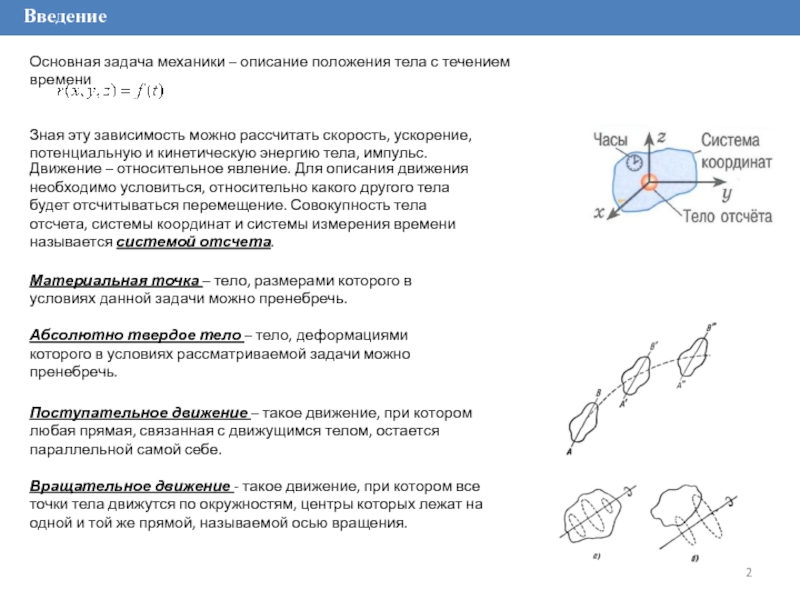
Материальная точка – тело, размерами которого в условиях данной задачи
можно пренебречь.
Абсолютно твердое тело – тело, деформациями которого в условиях
рассматриваемой задачи можно пренебречь.Поступательное движение – такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе.
Вращательное движение - такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
Движение – относительное явление. Для описания движения необходимо условиться, относительно какого другого тела будет отсчитываться перемещение. Совокупность тела отсчета, системы координат и системы измерения времени называется системой отсчета.
Основная задача механики – описание положения тела с течением времени
Зная эту зависимость можно рассчитать скорость, ускорение, потенциальную и кинетическую энергию тела, импульс.
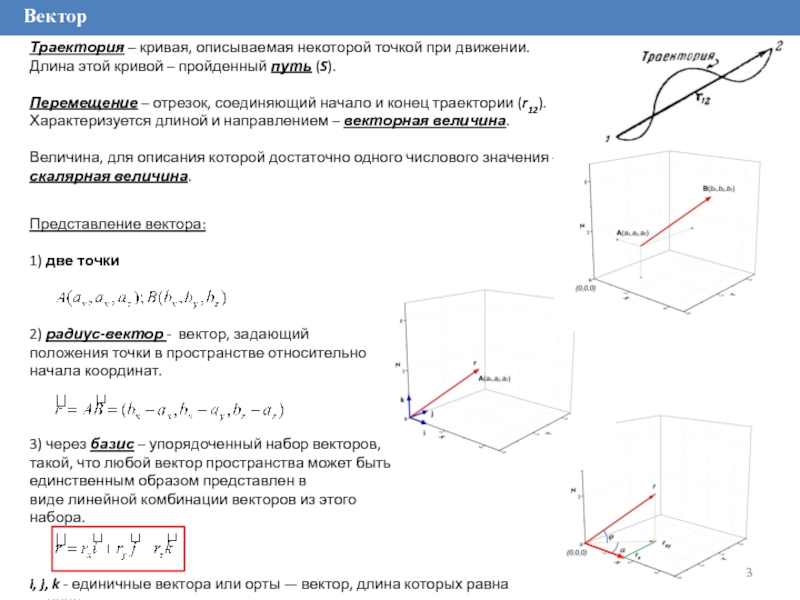
Слайд 3Вектор
Представление вектора:
1) две точки
2) радиус-вектор - вектор, задающий положения точки в пространстве относительно начала
координат.
3) через базис – упорядоченный набор векторов, такой, что любой вектор
пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора.Траектория – кривая, описываемая некоторой точкой при движении. Длина этой кривой – пройденный путь (S).
Перемещение – отрезок, соединяющий начало и конец траектории (r12). Характеризуется длиной и направлением – векторная величина.
Величина, для описания которой достаточно одного числового значения – скалярная величина.
i, j, k - единичные вектора или орты — вектор, длина которых равна единице.
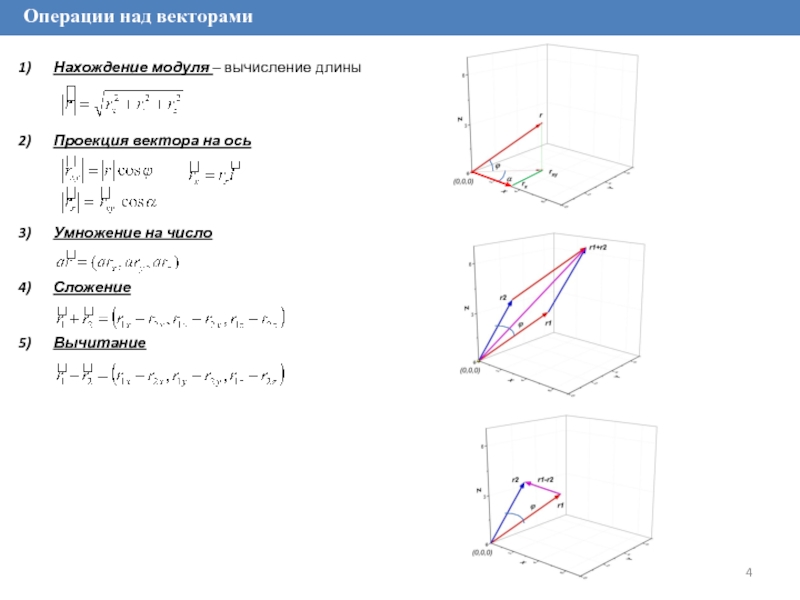
Слайд 4Операции над векторами
Нахождение модуля – вычисление длины
Проекция вектора на ось
Умножение
на число
Сложение
Вычитание
Слайд 5Операции над векторами
Скалярное произведение векторов - операция над двумя векторами, результатом
которой является число, характеризующее длины векторов-сомножителей и угол между ними.
Векторное произведение векторов -
вектор, перпендикулярный обоим исходным векторам, норма которого равна площади параллелограмма, образованного исходными векторами, а направление которого определяется по правилам правого винта.- через длины и угол
- через координаты
вращаем винт от первого множителя ко второму
- обозначение
- длина вектора
- координаты результирующего вектора
Слайд 6Скорость. Ускорение.
r1
r2
Δr
ΔS
x
y
Положение материальной точки в пространстве зададим радиус-вектором r. Перемещение
точки за время Δt будет соответствовать изменению радиус-вектора Δr, не
совпадающему в общем случае с ΔS.Скорость – векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта. Предел отношения dr к dt. Касательная к траектории.
В общем случае, в прямоугольной декартовой системе координат, скорость определяется
V1
Пройденный путь
V2
a
Слайд 7Скорость. Ускорение.
Скорость – векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно
выбранной системы отсчёта. Предел отношения dr к dt. Касательная к траектории.
Ускорение — векторная физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени.
В общем случае, в прямоугольной декартовой системе координат, ускорение определяется
Пройденный путь при равнопеременном движении
r1
r2
Δr
ΔS
x
y
V1
V2
a
Слайд 8Выразим ускорение через известные величины R и υ. Рассмотрим треугольник
134. Опустим перпендикуляр и учтем, что для малых углов:
Ускорение при
криволинейном движении Δϕ
1
2
0
3
4
υ
υ+Δυ
Δυ
υ+Δυ
ΔS
Δϕ
Δϕ
n’
n
R
R
R
R
ΔS
ΔS/2
Δϕ/2
Δϕ
υ
Δυ
Δυ/2
Δϕ/2
υ+Δυ
1
3
4
0
1
2
τ
Рассмотрим случай криволинейного движения. Ускорением называется изменение скорости, но скорость – векторная величина, а то есть, может изменятся как по величине, так и по направлению.
Рассмотрим движение по окружности радиусом R с постоянной скоростью υ. За время Δt точка сместиться из положения 1 в положение 2, совершив поворот на угол Δϕ и пройдя путь ΔS. Перенесем вектор скорости из точки 2 в точку 1 и найдем разность этих векторов. Получим равнобедренный треугольник 134. Вектор Δυ имеет направление n.
Ускорение можно представить в виде:
Нормальное ускорение - компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной 1/R, направлено к центру кривизны траектории.
При стремлении Δϕ, а значит и ΔS, к нулю, вектор n’ совпадет по направлению с нормалью n (перпендикуляром) к скорости υ.
То же самое сделаем для треугольника 012:
Представим эти выводы в формулу для ускорения:
Слайд 9Ускорение при криволинейном движении
1
2
0
3
4
υ
υ+Δυ
Δυn
υ+Δυ
ΔS
Δϕ
Δϕ
n’
n
R
R
τ
Если движение криволинейное (не окружность), то
вектор скорости υ изменяется как по направлению, так и по
величине. Изменение вектора скорости Δυ можно разложить на компоненты: Δυτ и Δυn, сонаправленные с единичными векторами n’ и τ’ (при стремлении Δϕ к нулю, эти вектора совпадут c векторами n и τ).В общем виде ускорение можно найти представив скорость в виде (величина скорости умножить на направление скорости):
Нормальное ускорение an - компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной 1/R, направлено к центру кривизны траектории.
τ’
Δυτ
Δυ
Производная произведения. Вторая компонента описывает изменение скорости по направлению, значение было найдено ранее.
Тангенциальное ускорение aτ — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости.
Слайд 10Вращение с постоянной угловой скоростью характеризуется временем полного оборота –
период T.
Величина обратная периоду называется частотой вращения, соответствует числу оборотов
за единицу времени.Вращательно движение
При вращательном движение все точки твердого тела движутся по окружностям, центры которых лежат на общей оси OO. Радиус вектор каждой точки ri за время Δt поворачивается на один и тот же угол Δϕ. При этом пройденный путь ΔSi может быть разным.
Вращательное движение характеризуется угловой скоростью ω.
Угловая скорость – векторная физическая величина, характеризующая изменение углового положения материальной точки относительно центра вращения. Указывает направление вращения и численно равна углу описываемому радиус-вектором точки за единицу времени.
Изменение угловой скорости, как по величине, так и по направлению, характеризуется угловым ускорением:
Вектор углового ускорения β сонаправлен с вектором угловой скорости ω если точка ускоряется, и направлен противоположно, если точка замедляется.
Вектор угловой скорости ω всегда ориентирован вдоль оси вращения.
Направление вектора ω определяется по правилу правого винта: искомый вектор ориентирован по направлению поступательного движения правого винта при его повороте, совпадающем с направлением вращения рассматриваемой точки.
Слайд 11Связь поступательного и вращательного движения
Во вращающемся теле угловая скорость ω
всех точек одинакова. Однако в зависимости от радиуса описываемой окружности
R точки могут проходить разный путь ΔS, а значит будут иметь разную линейную скорость υ. Найдем взаимосвязь между угловой и линейной скоростью.За время Δt точка повернется на угол Δϕ. Точка находящаяся на расстояние R от оси вращения, проходит при этом путь ΔS. Выразим пройденный путь через угол рассматривая равнобедренный треугольник 012 (как в случае нахождения нормального ускорения):
Подставим это выражение в формулу определения скорости:
Полученная взаимосвязь интересна тем, что все три величины уравнения являются векторными: вектор угловой скорости ω направлен по оси, радис-вектор R проводится от оси вращения до точки, линейная скорость υ – касательная к траектории.
Если результатом перемножения двух векторов является третий вектор, ориентированный перпендикулярно плоскости образованной двумя исходными векторами, то такая взаимосвязь описывается векторным произведением:
2
υ
ΔS
Δϕ
R
1
ω
R
0