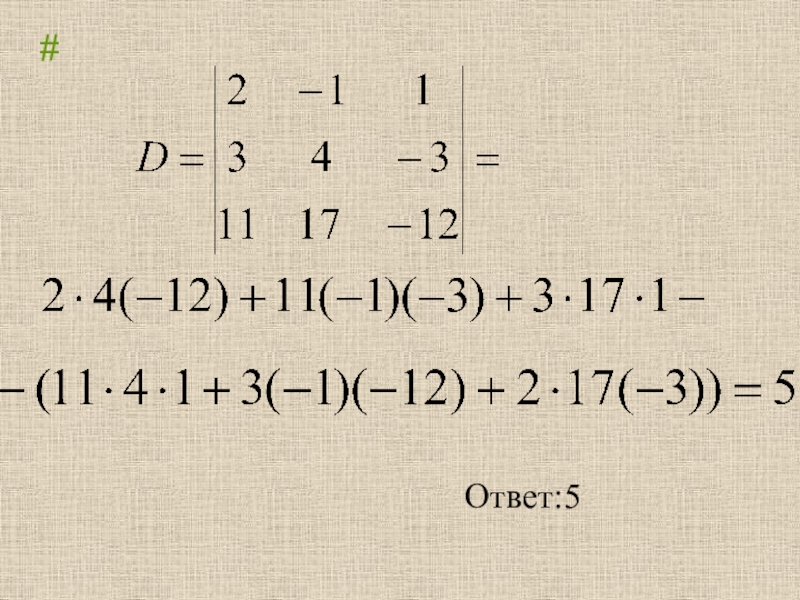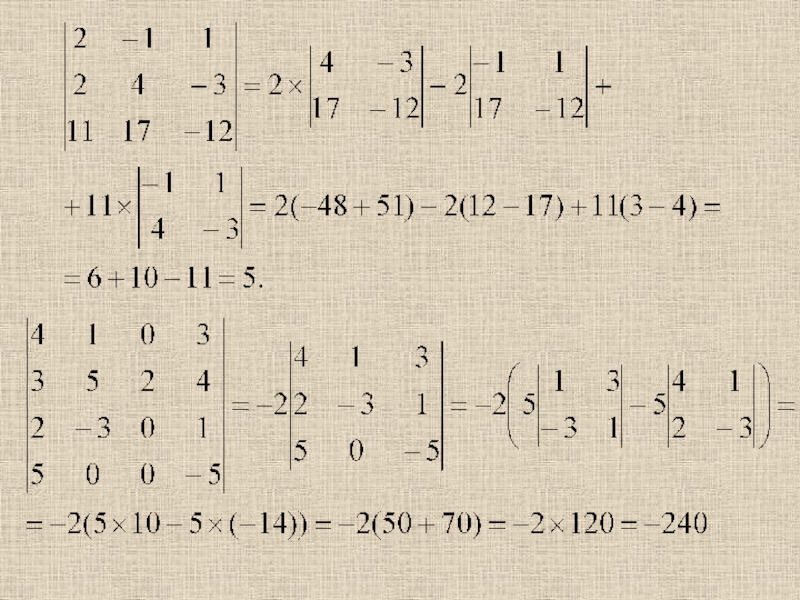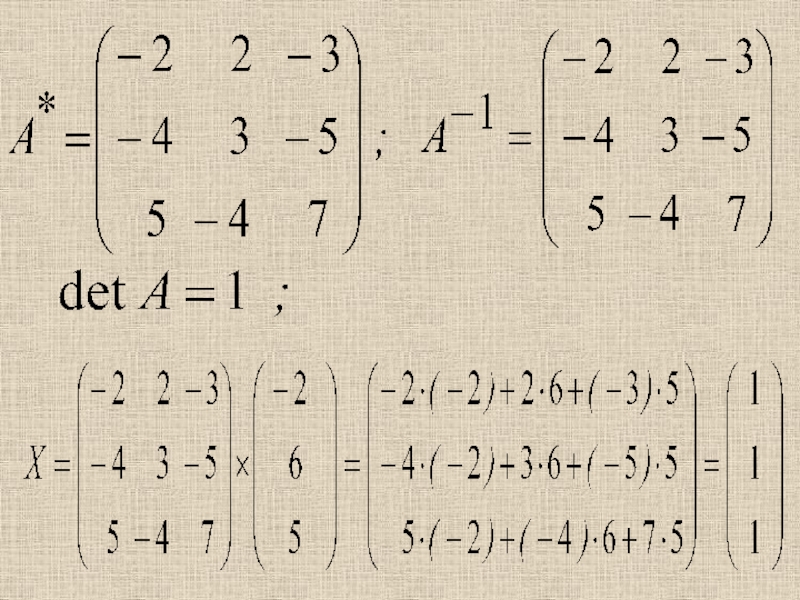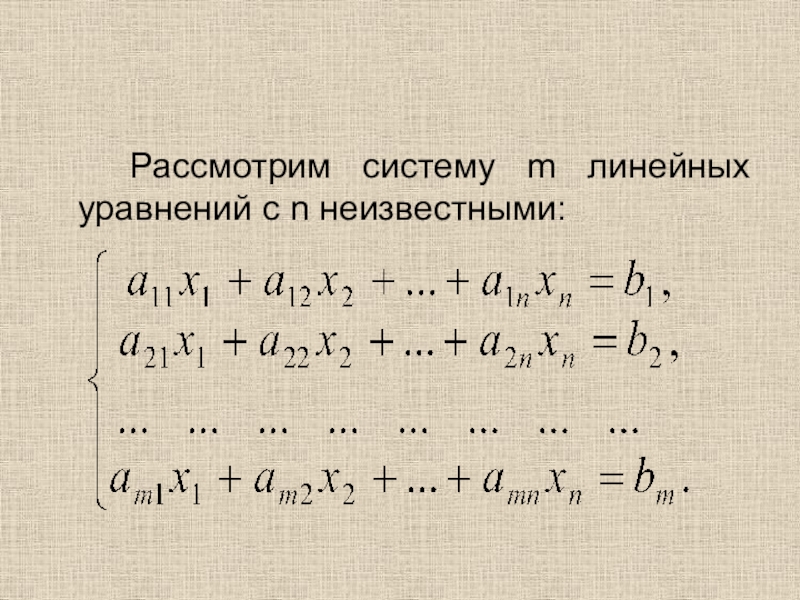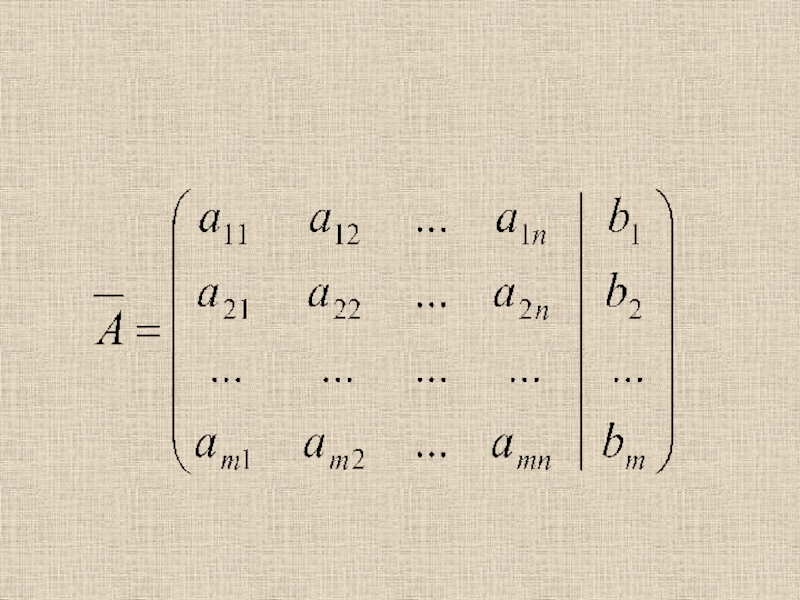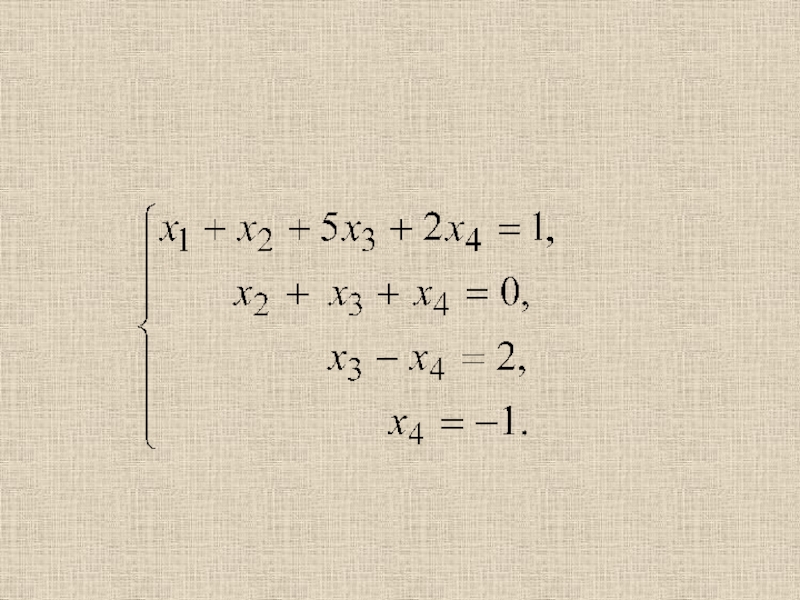Слайд 1ЛЕКЦИЯ №2
ТЕМА ЛЕКЦИИ:
«ЛИНЕЙНАЯ АЛГЕБРА»
2 часть
Слайд 2Матрицы
Элементарные преобразования и действия над матрицами
made by aspirin
Слайд 3Определение: Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой
длины (или n столбцов одинаковой длины)
Матрицу А называют матрицей
размера m x n
Матрица А имеет m-строк и n- столбцов /колонн/; говорят, что она имеет размер. Всего в матрице размера m x n имеется mn элементов.
Слайд 4Классификация матриц
1. Матрицы полагаются равными при совпадении у них соответствующих
элементов. Это записывается так: А=В.
2. Матрица, у которой число строк
равно числу столбцов называется квадратной. Квадратную матрицу размера n x n называют матрицей n – го порядка.
3. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
4. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.
Слайд 55. Квадратная матрица называется треугольной, если все элементы, расположенные по
одну сторону от главной диагонали равны нулю.
6. Матрица, все элементы
которой равны нулю, называется нулевой. Обозначается буквой О.
7. Матрица, содержащая один столбец или одну строку, называется вектором (или вектор – столбец, или вектор - строка).
8.Матрица АТ называется транспонированной к А, если в матрице А строки заменены на столбцы соответствующих номеров:
Слайд 6Элементарные преобразования матриц
1. Перестановка местами двух параллельных рядов
матрицы;
2. Умножение всех элементов ряда матрицы на число
отличное от нуля;
3. Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А В.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической.
Слайд 7Действия над матрицами
Суммой матриц одинакового размера называется матрица, элементы которой
равны сумме соответствующих элементов матриц-слагаемых. Обозначение: А+В. Аналогично определяется разность
матриц.
При умножении матрицы на число, умножаются все элементы данной матрицы.
Слайд 8Операция умножения двух матриц вводится только для случая, когда число
столбцов первой матрицы равно числу строк второй матрицы. Такие матрицы
называются согласованными (n × m и m × k)
Произведением 2-х согласованных матриц и называется матрица размера , элементы которой вычисляются по формуле:
Cij=ai1∙b1j+ai2∙b2j+….+aikbkj+…..+ain∙bnj
Таким образом, элементом новой матрицы является , который равен сумме произведений элементов n строки первой матрицы на соответствующие элементы k столбца второй матрицы.
Возможно умножение матрицы на вектор-столбец справа и на вектор-строку слева.
Слайд 9Свойства произведения матриц
1. А × О = О
2. А ×
Е = А
3. А × В ≠ В × А
4.
α (АВ) = (αА) × В = А × (αВ)
5. АВС = (АВ) × С = А × (ВС)
6. А (В + С) = АВ + АС,
Слайд 10=( 9.3+2(-4)+3.1; 9.2+2.0+3.7; 91+2.5+3.2; 9.4+2.6+3.1) =
=( 22, 39, 25, 51).
Слайд 12
Квадратной матрице А порядка n можно сопоставить число det A,
называемое ее определителем, следующим образом:
1. n = 1. А =
(a1); det A = a1
2. n = 2.
3. n = 3.
Слайд 14Определитель n-го порядка.
Записывается в виде квадратной таблицы, содержащей
n2 элементов
вида a ik , расположенных в n строках
и n
столбцах:
Слайд 15Минор элемента аik
Минором некоторого элемента aik определителя n-го порядка
называется определитель n-1 –го, полученный из исходного путем вычеркивания строки
и столбца, на пересечении которых находится выбранный элемент и обозначается Мik.
# a23=4
M23=
M31=5 M14=11
Слайд 16Алгебраическое дополнение Aik
Алгебраическим дополнением элемента aik данного D
называется Мik , взятый со знаком «+», если (i+k)- четное
число, и со знаком «-», если (i+k)- нечетное число.
Для предыдущего примера:
А23=-М23=-13
А31=М31=5
А14=-М14=-11
Формула Лапласа.
Теорема: Определитель равен сумме произведений элементов всякой его строки (столбца) на их алгебраические дополнения.
Слайд 182. Перестановка любых двух строк (столбцов) , меняет только знак
D.
D’=-D
Свойства определителей.
1. Транспонирование определителя , т.е. замена строк столбцами и
наоборот, не меняет его значения.
Слайд 193. Общий множитель всех элементов одной строки (столбца) м.б. вынесен
за знак D.
4. Если соответствующие элементы двух строк (столбцов)
равны или пропорциональны, то определитель равен 0.
Слайд 206. Если к элементам одной строки (столбца) определителя прибавить соответственные
элементы другой строки или одинаковые пропорциональные им числа ,то исходный
определитель не изменится.
5. Если элементы какой-либо строки (столбца) состоят из двух слагаемых, то определитель равен сумме двух определителей, различающихся между собой только элементами одной строки (столбца), бывшими ранее отдельными слагаемыми.
Слайд 21Рангом матрицы А называется наивысший порядок отличного от нуля минора
этой матрицы.
Ранг матрицы А обозначается rangA или r(A).
Из определения
следует:
1. Ранг матрицы Аmxnне превосходит меньшего из ее размеров.
2. r(А)=0 тогда и только тогда , когда все элементы матрицы равны 0.
3. Для квадратной матрицы n-ого порядка r(А)=n, тогда и только , когда матрица А – невырожденная.
Слайд 22Пример.
Найти ранг матрицы
Решение:
Все миноры 3-ого порядка равны нулю. Есть минор
2-го порядка, отличный от нуля
. Значит, ранг данной матрицы
равен двум (rang А=2)
Ответ: r(А)=2
Слайд 23Свойства ранга матрицы
1. При транспонировании матрицы
ее ранг не меняется.
2. Если вычеркнуть
из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.
Пример: найти ранг матрицы
rang A = 2
Слайд 24Решение систем линейных уравнений.
Матричный метод.
Формулы Крамера.
Слайд 25Невырожденные матрицы
Квадратная матрица А называется невырожденной, если определитель не
равен нулю. В противном случае матрица А называется вырожденной.
Матрицей,
союзной к матрице А, называется матрица
Где Аik - алгебраическое дополнение элемента аik данной
матрицы А.
Слайд 26Матричный метод решения системы
Матричная запись системы
Слайд 27 В матричном виде: АХ = В, где
А
- основная матрица системы;
Х – матрица-столбец переменных;
В –
матрица-столбец свободных членов.
Если А – невырожденная, т.е. ∆ ≠ 0 и А имеет единственную А-1 , то
А-1 АХ = А-1В, т.е.
Х = А-1В – решение системы уравнений
Алгоритм нахождения А-1
1) det А ≠ 0
2) составить для А союзную матрицу А*
3) умножить А* на 1/∆ → А-1
Слайд 28Алгоритм решения систем линейных уравнений матричным методом
1. Составляем матрицы А,
В и Х
2. Вычисляем определитель матрицы А
3. Находим обратную матрицу
А-1
4. Находим решение системы уравнений по формуле:
Х=А-1В
Слайд 31Формулы Крамера
Если определитель системы n линейных уравнений с n неизвестными
D≠0, то система совместна и имеет единственное решение, выражаемое по
следующим формулам:
Dn – это определитель, который получается из определителя системы путем замены только n-го столбца столбцом свободных коэффициентов системы.
Слайд 32Алгоритм решения систем линейных уравнений по формулам Крамера
1. Составляем матрицы
А, В, Х
2. Вычисляем определитель матрицы А.
3. Составляем определитель 1
путем замены первого столбца в матрице А на вектор-столбец матрицы В
4.Вычисляем определитель 1 и находим первую неизвестную по формуле:
5. Составляем определитель 2 путем замены второго столбца в матрице А на вектор-столбец матрицы В
Слайд 336. Вычисляем определитель 2 и находим вторую неизвестную по формуле:
7.
Составляем определитель 3 путем замены третьего столбца в матрице А
на вектор-столбец матрицы В
8. Вычисляем определитель 3 и находим третью неизвестную по формуле:
Слайд 34Решение систем линейных уравнений методом Гаусса
Одним из универсальных и эффективных
методов решений линейных алгебраических уравнений систем является метод Гаусса, состоящий
в последовательном исключении неизвестных.
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (треугольному) виду. На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Слайд 35 Рассмотрим систему m линейных уравнений с n неизвестными:
Слайд 36 Назовем матрицей системы матрицу, составленную из коэффициентов при
неизвестных. Матрицу, полученную из А добавлением столбца свободных членов, называют
расширенной матрицей:
Слайд 38Теорема Кронекера–Капелли
Для того чтобы система линейных уравнений была
совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен
рангу ее расширенной матрицы, т.е.
Слайд 39 Если ранг матрицы совместной системы равен числу неизвестных,
то система имеет единственное решение, если же ранг меньше числа
неизвестных, то система имеет множество решений.
Слайд 40Две системы, множества решений
которых совпадают,
называются
эквивалентными или равносильными.
Преобразование, применение которого
превращает
систему в новую
систему, эквивалентную исходной,
называется эквивалентным или
равносильным преобразованием.
Слайд 41Пример
Исследовать систему линейных уравнений
Слайд 42 Составим расширенную матрицу системы и с помощью элементарных
преобразований вычислим одновременно ранги обеих матриц.
Слайд 43Метод Гаусса
Для того чтобы решить систему уравнений
методом Гаусса
выписывают расширенную матрицу этой системы и над
строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы
будут располагаться нули.
Слайд 44 Разрешается:
1) изменять порядок строк матрицы, что соответствует
изменению порядка уравнений;
2) умножать строки на любые
отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа;
3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число.
Слайд 45 С помощью этих преобразований каждый раз получается расширенная
матрица новой системы, равносильной исходной, т. е. такой системы, решение
которой совпадает с решением исходной системы
Слайд 46Установить совместность и решить систему
Слайд 47 Выпишем расширенную матрицу системы и поменяем местами первую
и вторую строки для того, чтобы элемент равнялся единице (так
удобнее производить преобразования матрицы).
Слайд 50Обратный ход
Ранги матрицы системы и ее расширенной матрицы
совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна
и решение ее единственно.
Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований:
Далее, подставляя его в третье уравнение, найдем
Подставляя и во второе уравнение, получим и, наконец, подставляя в первое уравнение найденные неизвестные, получим Таким образом, имеем решение системы
Слайд 53Общее решение системы линейных уравнений
Если ранг матрицы
равен , то любой отличный от нуля минор
порядка этой матрицы называется базисным.
Слайд 55 Выпишем расширенную матрицу системы и преобразуем ее
Слайд 57 Теорема о совместности
однородной системы
Для того чтобы однородная
система
линейных уравнений имела нетривиальное решение, необходимо и достаточно, чтобы ранг матрицы этой системы был меньше числа
неизвестных n.
т.е. имеет бесчисленное множество решений, в том числе и нетривиальное.
Если m=n, т.е. число уравнений совпадает с числом неизвестных, матрица системы является квадратной. условие r
Слайд 60 Составим матрицу системы
и методом элементарных преобразований найдем
ее ранг.
Слайд 62 Выберем в качестве базисного минор
Тогда
укороченная система имеет вид
Слайд 64Фундаментальная система решений
Назовем фундаментальной системой решений систему матриц-столбцов,
полученную из общего решения при условии, что свободным неизвестным дают
последовательно значения
Слайд 65 Матрицы-столбы, т.е. фундаментальную систему решений обозначают Е1, Е2,
…, Еn. Общее решение будет представлено в виде
Слайд 66 Из общего решения последней системы найдем фундаментальную систему
решений.
,
Общее решение можно записать в виде
Слайд 67Решение систем линейных уравнений методом Гаусса
Одним из универсальных и эффективных
методов решений линейных алгебраических уравнений систем является метод Гаусса, состоящий
в последовательном исключении неизвестных.
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (треугольному) виду. На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Слайд 68Система уравнений называется совместной, если она имеет хотя бы одно
решение, и несовместной, если она не имеет ни одного решения.
Совместная
система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Предыдущей пример демонстрирует совместную определенную систему линейных уравнений.
Если система неопределенная каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Слайд 69Решить систему (несовместную) методом Гаусса
Переставим местами первую и вторую строки
Слайд 70Умножим элементы второй строки на (-2) и прибавим к соответственным
элементам третьей строки.
Третьей строке соответствует уравнение: 0∙x+0∙y+0∙z = -4
Равенство неверное решений нет.
Ответ: система несовместна.