ЛЕКЦИЯ №2 ОДНОФАЗНЫЙ ПЕРЕМЕННЫЙ ТОК

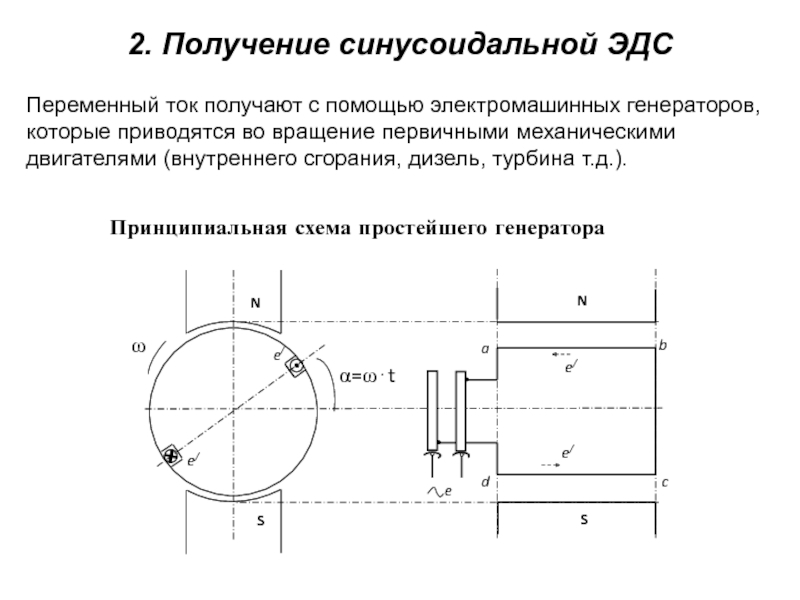
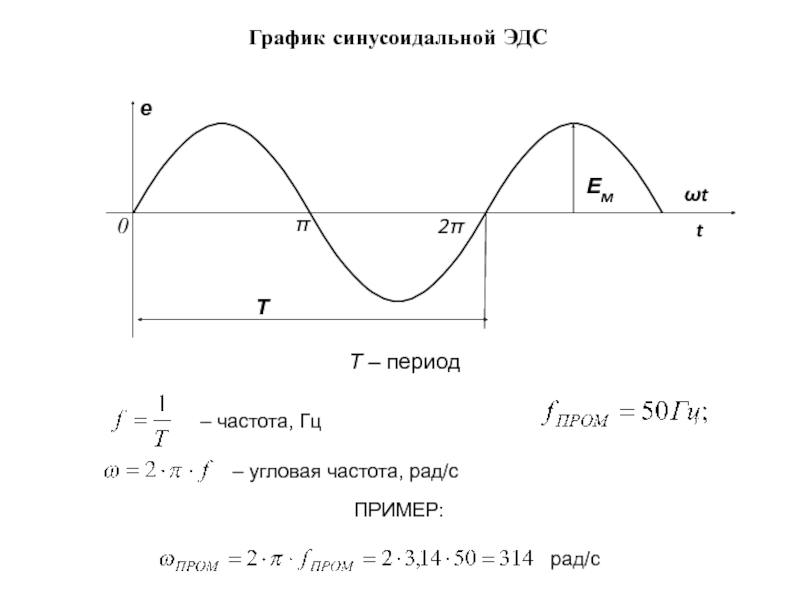
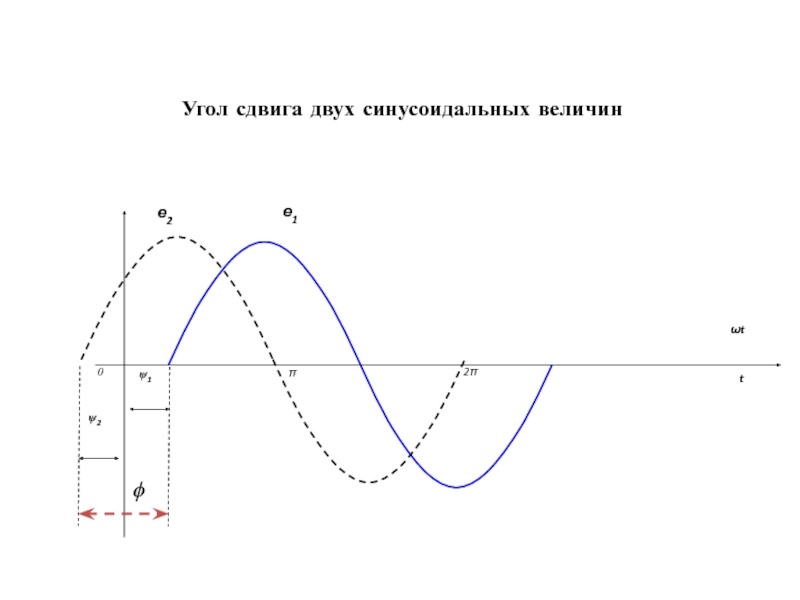
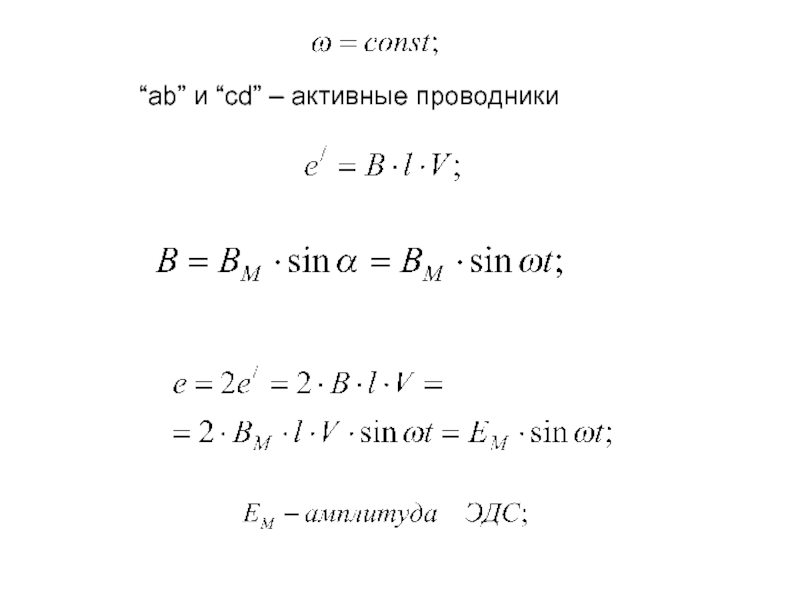их значения изменяются во времени.

В современной технике получили применения переменные

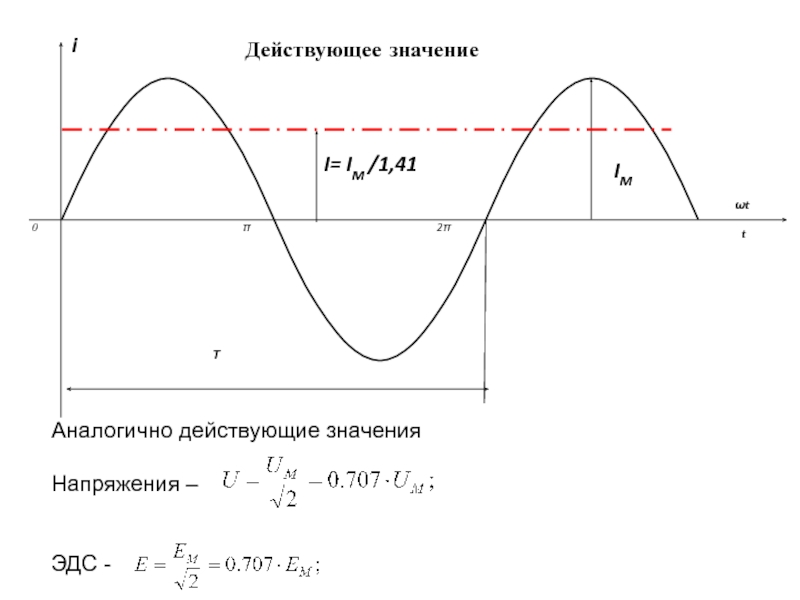
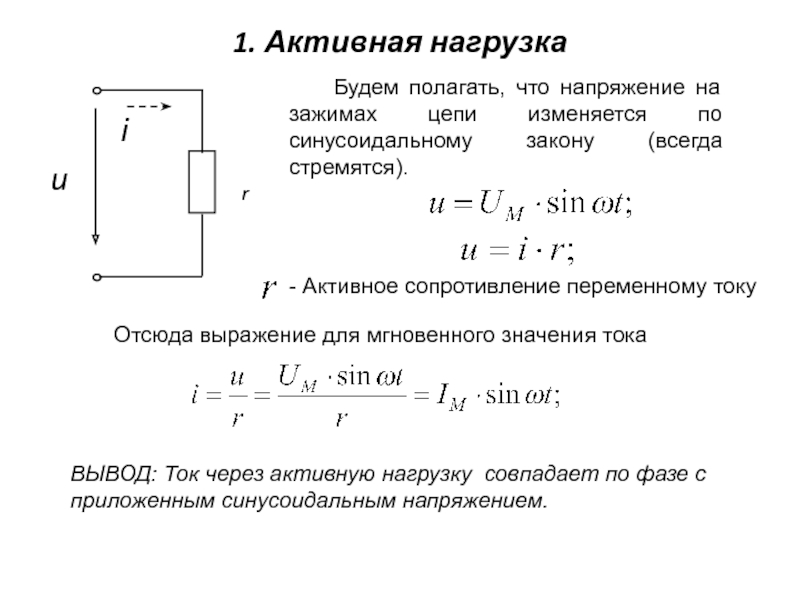
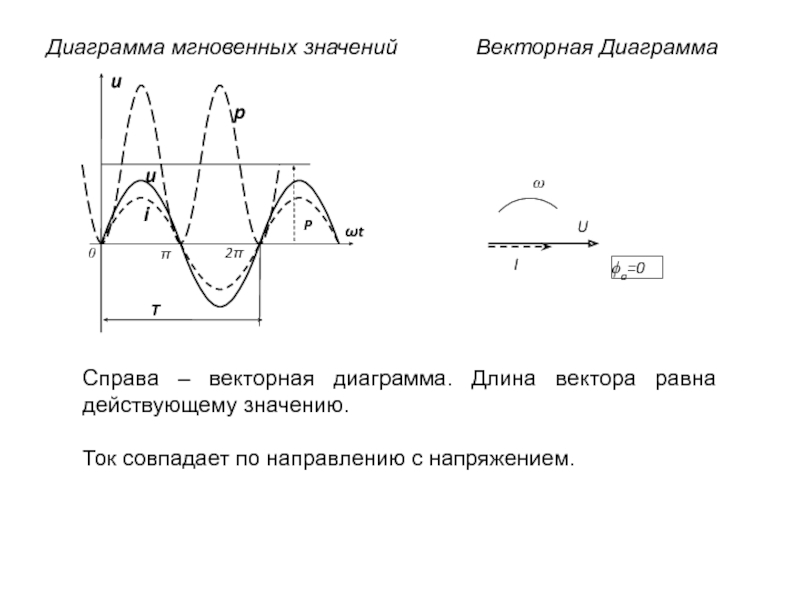
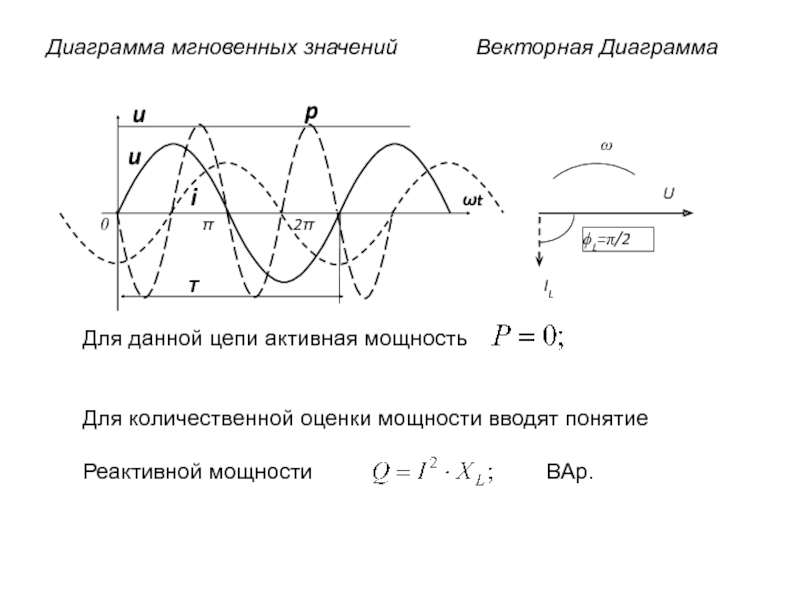
токи. Изменяющиеся во времени по синусоидальному закону, т.к. позволяют наиболее экономично осуществлять производство, распределение, преобразование и использование электрической энергии.

Значения величин в данный момент времени называются МГНОВЕННЫМИ, они обозначаются малыми буквами: t, e, u, i, p.

t, e, u, i, p – мгновенные значения ЭДС, напряжения, тока, мощности.

Рассмотренные ранее законы Кирхгофа справедливы для мгновенных значений соответствующих величин.


Применение однофазного переменного тока:

для питания осветительных установок,
систем сигнализации и контроля.

которые приводятся во вращение первичными механическими двигателями (внутреннего сгорания, дизель,

турбина т.д.).

Принципиальная схема простейшего генератора

=t



скоростью .
В пазах сердечника расположен виток проволоки. Его концы присоединены

к вращающимся контактным кольцам, к которым прижимаются неподвижные щетки, обеспечивающие связь неподвижных потребителей с вращающейся цепью.

При вращении витка в его активных проводниках “ab” и “cd” по закону ЭМИ наводится ЭДС. Полюсам магнита придают специальную форму, чтобы магнитная индукция в зазоре вдоль окружности сердечника изменялась по синусоидальному закону.
Активные проводники “ab” и “cd” витка соединены последовательно, поэтому результирующая ЭДС, снимаемая со щеток в два раза больше, чем в каждом из активных проводников.

Принцип действия синхронного генератора

рад/с
ПРИМЕР:
рад/с

зависимость
Если в пазах сердечника размещены два витка, сдвинутые относительно друг

друга, то и индуктируемые ЭДС будут сдвинуты.

Выделяют два случая:

– то говорят, что функции совпадают

по фазе;

– то говорят, что функции находятся в противофазе;

и ЭДС судят по их среднеквадратичным значениям.
Рассмотрим синусоидальный ток



Среднеквадратичное значение

такого тока равно:





ОПРЕДЕЛЕНИЕ: В Электротехнике среднеквадратичные значения тока, напряжения, ЭДС называется действующими.

Под действующим значением переменного тока понимается такое значение постоянного тока, которое по тепловому действию за период эквивалентно переменному.

электровыпрямительных установок используются средние значения

Рассмотрим синусоидальную ЭДС



Среднее значение такой

ЭДС равно:

Средние значение переменных тока и напряжения

работы электрических цепей переменного тока приходится складывать синусоидальные функции времени

одной и той же частоты, но имеющие разные амплитуды и начальные фазы. Это удобно выполнять если синусоидальные функции изображать вращающимися векторами.
Пусть нам задано мгновенное значение в виде:

Рассмотрим два момента времени: t=0; t=t1;
Справа изобразим график синусоидальной ЭДС, слева – окружность, радиус которой ОА равен амплитудному значению ЭДС ЕМ .
Радиус-Вектор ОА=ЕМ вращается с угловой скоростью , равной угловой частоте изменения ЭДС. Тогда в любой момент времени по радиус-вектору можно определить мгновенный значения ЭДС, которые будут равны проекции длины вектора на вертикальную ось Y.

сложения функций к геометрическому сложению изображающих их векторов.

одной частоты




Для этого необходимо на одном графике изобразить соответствующие

вектора:

амплитудному значению результирующего тока.

ОПРЕДЕЛЕНИЕ: Векторной диаграммой называется совокупность нескольких векторов,

изображающих на одном графике синусоидальные функции времени одной частоты.


На практике, при построении векторных диаграмм длину вектора принимают равной не амплитудному, а действующему значению.


Один из векторов принимают за исходный, а остальные строятся по отношению к нему с соответствующим сдвигом фаз, при этом отпадает необходимость использовать оси Х и Y.

цепи изменяется по синусоидальному закону (всегда стремятся).
Отсюда выражение для мгновенного

значения тока

ВЫВОД: Ток через активную нагрузку совпадает по фазе с приложенным синусоидальным напряжением.

- Активное сопротивление переменному току

и переходят к действующим значениям
– Закон Ома для цепи с

активной нагрузкой

периодическому закону с двойной частотой относительно приложенного напряжения.
2) Мощность всегда

положительна. Это означает, что поступающая от сети электроэнергия необратимо преобразуется в другой вид энергии (в данном случае –в тепло)

равна действующему значению.

Ток совпадает по направлению с напряжением.

значению за период. Такая мощность называется активной.
(Произведение действующих значений.)

закону Кирхгофа
По закону ЭМИ в катушке будет индуктироваться ЭДС, которая

называется ЭДС самоиндукции. При отсутствии ферромагнитных материалов потокосцепление пропорционально току, а коэффициентом пропорциональности является индуктивность.

уравнения получим
ВЫВОД:
Ток через индуктивную нагрузку отстает по фазе от

приложенного синусоидального напряжения на угол

и перейдем к действующим значениям
– Закон Ома для цепи с

индуктивной нагрузкой

– индуктивное сопротивление, Ом;

периодическому закону с двойной частотой относительно приложенного напряжения.
2)Анализ показывает:
–

когда ток и напряжение совпадают по направлению – мощность положительна;
– когда ток и напряжение не совпадают по направлению – мощность отрицательна;

количественной оценки мощности вводят понятие

Реактивной мощности

ВАр.