Слайд 1Лекция №2
Системы счисления.
Основные понятия математической логики.
Фролова Юлия Борисовна
Слайд 2Контрольные вопросы по теме:
Системы счисления (СС)
Что называется системой счисления?
Типы
систем счисления.
Что называется основанием системы счисления?
Какие системы счисления
применяются в компьютере для представления информации?
Правила перевода чисел из одной СС в другую.
Правила выполнения перевода из прямого в обратный и обратный дополнительный код.
Правила выполнения арифметических операций в двоичной системе счисления.
Слайд 5
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
444
–
4 сотни,
4 десятка, 4 –единицы,
400 – ноли нужны для обозначения
позиции числа 4
Слайд 6Система счисления
это способ представления любого числа с помощью алфавита
символов, называемых цифрами.
Основание системы счисления
это количество символов в ее алфавите
(количество цифр, необходимых для записи числа в системе).
Алфавит 2-ой с.с.: 0 1
8-ой с.с.: 0 1 2 3 4 5 6 7
10-ой с.с.: 0 1 2 3 4 5 6 7 8 9
16-ой с.с.: 0 1 2 3 4 5 6 7 8 9 A B C D E F
11102, 2458, 5910, А17816
Слайд 7Типы систем счисления
Позиционная
значение каждой цифры определяется ее позицией в записи
числа;
S - основание системы счисления;
А - цифры числа, записанного
в данной системе счисления;
n - количество разрядов числа.
Непозиционная
значение цифры не зависит от ее места в записи числа.
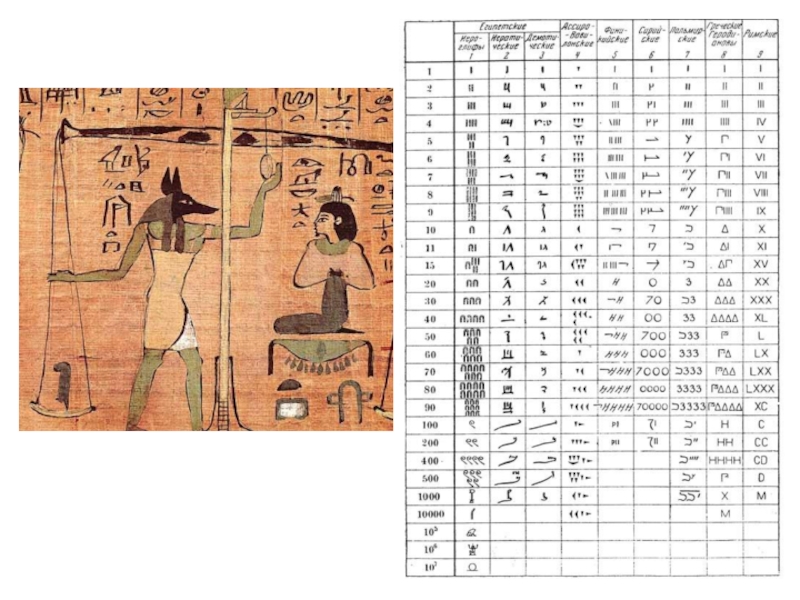
(в римской системе счисления:
I – один, X – десять, C – сто, M – тысяча
и их половины:
V – пять, L – пятьдесят, D – пятьсот)
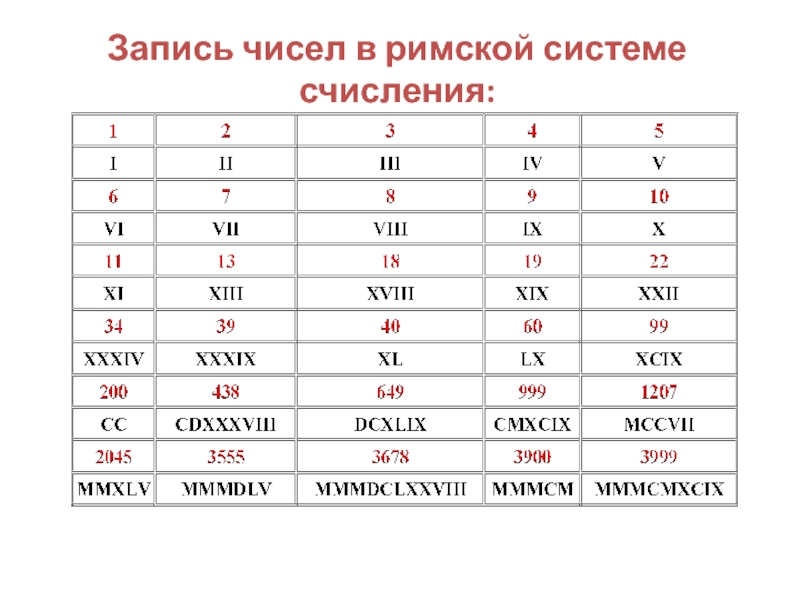
Слайд 8Запись чисел в римской системе счисления:
Слайд 9пример:
- Позиционная система счисления
256 > 143 , т.к. 2 >1
Непозиционные
системы счисления
IX > VI , несмотря на то, что I
< V
Слайд 11ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
(decimal)
Слайд 12Двоичная система счисления
(binary)
Основание этой системы счисления равно двум.
Используется две цифры
- 0 и 1
Примеры записи двоичного числа:
4610=1011102
510=1012
Недостатки двоичной системы счисления
-
большое количество разрядов, требующихся для записи чисел.
Преимущество - простота выполнения арифметических действий.
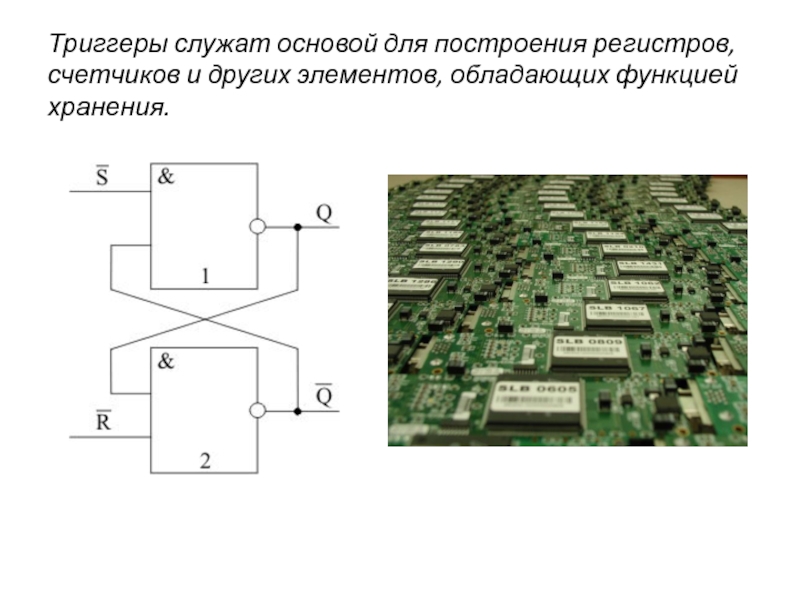
Слайд 13Триггеры служат основой для построения регистров, счетчиков и других элементов,
обладающих функцией хранения.
Слайд 14Восьмеричная система счисления
(octal)
Основание этой системы счисления = 8.
Используются
цифры - 0, 1, 2, 3, 4, 5, 6 и
7.
Пример записи восьмеричного числа:
A8=1258=1*82+2*81+5*80 =6410+1610+510= 8510
Слайд 15Шестнадцатеричная система счисления
(hexadecimal)
Основание этой системы счисления = 16.
В качестве
цифр в шестнадцатеричной системе используются символы –
0, 1, 2,
3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Слайд 1811100102=126+125+124+023+022 +121+020=11410
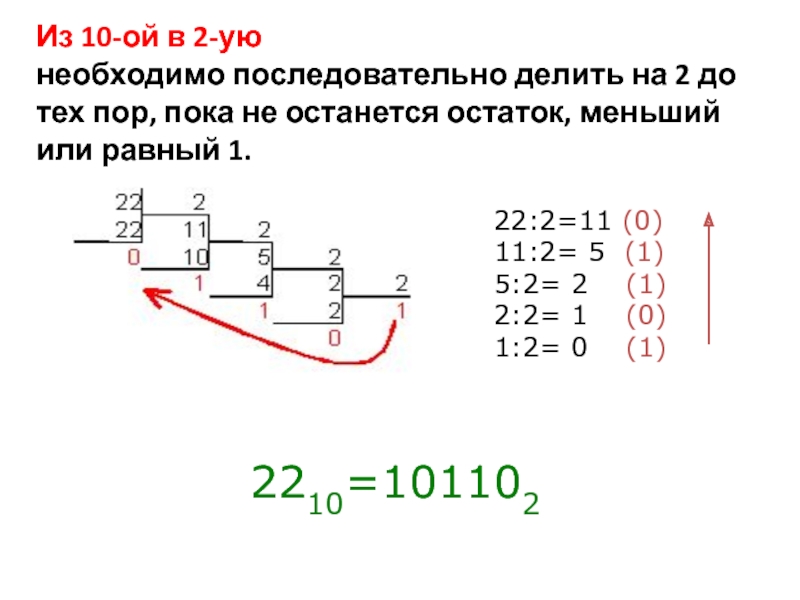
Слайд 21Из 10-ой в 2-ую
необходимо последовательно делить на 2 до
тех пор, пока не останется остаток, меньший или равный 1.
22:2=11 (0)
11:2= 5 (1)
5:2= 2 (1)
2:2= 1 (0)
1:2= 0 (1)
2210=101102
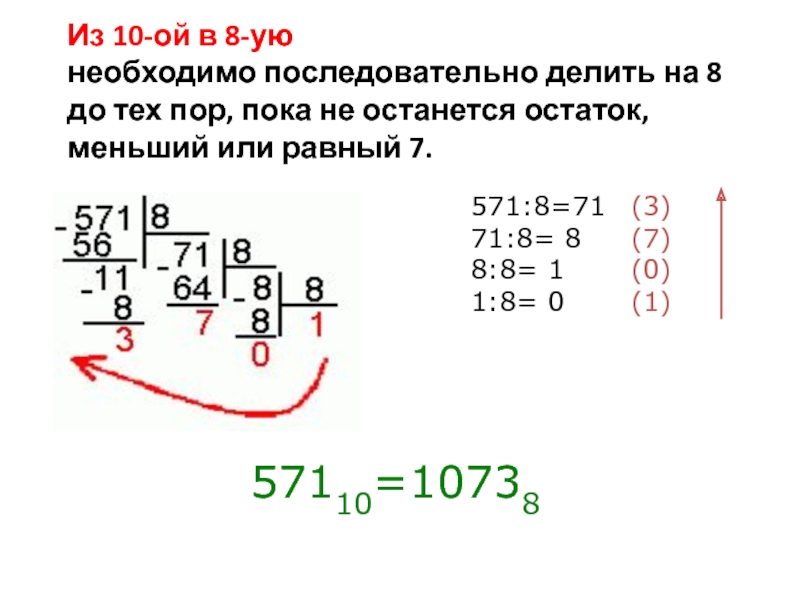
Слайд 22Из 10-ой в 8-ую
необходимо последовательно делить на 8 до
тех пор, пока не останется остаток, меньший или равный 7.
571:8=71 (3)
71:8= 8 (7)
8:8= 1 (0)
1:8= 0 (1)
57110=10738
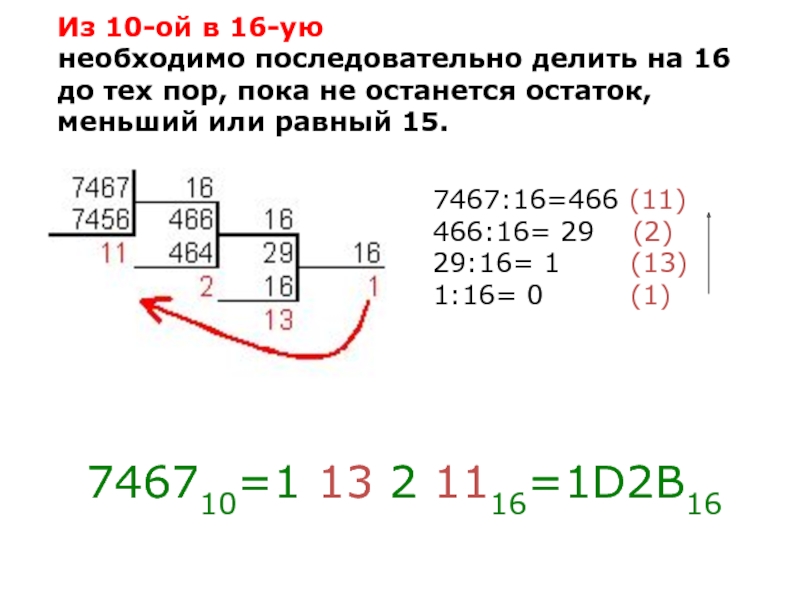
Слайд 23Из 10-ой в 16-ую
необходимо последовательно делить на 16 до
тех пор, пока не останется остаток, меньший или равный 15.
7467:16=466 (11)
466:16= 29 (2)
29:16= 1 (13)
1:16= 0 (1)
746710=1 13 2 1116=1D2B16
Слайд 24Из 2-ой в 8-ую
разбить на триады (тройки цифр), начиная с
младшего разряда и каждую триаду заменить соответствующей 8-ой цифрой.
10010112=
001. 001. 011. = 1138
Из 2-ой в 16-ую
разбить на тетрады (четверки цифр), начиная с младшего разряда и каждую тетраду заменить соответствующей 16-ой цифрой.
10111000112=0010. 1110. 0011.=2. 14 .3. = =2E38
Слайд 25Из 8-ой в 2-ую
каждую цифру заменить эквивалентной ей двоичной триадой.
5318=101 011 0012
Из 16-ой в 2-ую
каждую цифру заменить эквивалентной ей
двоичной тетрадой.
EE816=1110 1110 10002
Слайд 26Из 8-ой в 16-ую и обратно
необходим промежуточный перевод чисел
в двоичную систему.
FEA16=1111 1110 10102
111 111 101 0102=77528
Слайд 27Коды чисел
Использование кодов позволяет свести вычитание чисел к арифметическому сложению
кодов этих чисел.
Коды чисел:
прямой,
обратный ,
дополнительный.
Слайд 28Прямой код
Cовпадает по изображению с записью самого числа.
Значение знакового
разряда для положительных чисел равно 0, а для отрицательных чисел
1.
Знаковым разрядом является крайний разряд в разрядной сетке.
В случае, когда для записи кода выделен один байт:
для числа +1101 прямой код 0,0001101,
для числа -1101 прямой код 1,0001101.
Слайд 29Обратный код
Для положительного числа совпадает с прямым кодом.
Для отрицательного
числа все цифры числа заменяются на противоположные (1 на 0,
0 на 1), а в знаковый разряд заносится единица.
Для числа +1101
прямой код 0,0001101;
обратный код 0,0001101.
Для числа -1101
прямой код 1,0001101;
обратный код 1,1110010.
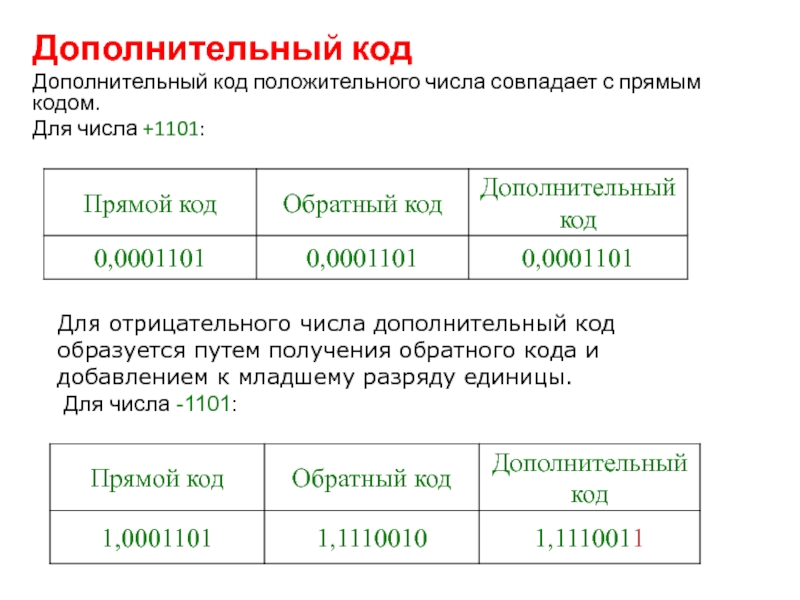
Слайд 30Дополнительный код
Дополнительный код положительного числа совпадает с прямым кодом.
Для
числа +1101:
Для отрицательного числа дополнительный код образуется путем получения
обратного кода и добавлением к младшему разряду единицы.
Для числа -1101:
Слайд 32Основные понятия
математической логики
Слайд 33Контрольные вопросы по теме:
Основные понятия
математической логики
Высказывание. Типы высказываний.
Составляющие логического
выражения.
Отрицание, таблица истинности отрицания.
Конъюнкция, таблица истинности.
Дизъюнкция, таблица истинности.
Импликация, таблица истинности.
Эквиваленция,
таблица истинности.
Приоритет логических операций.
Система аксиом, законы алгебры логики.
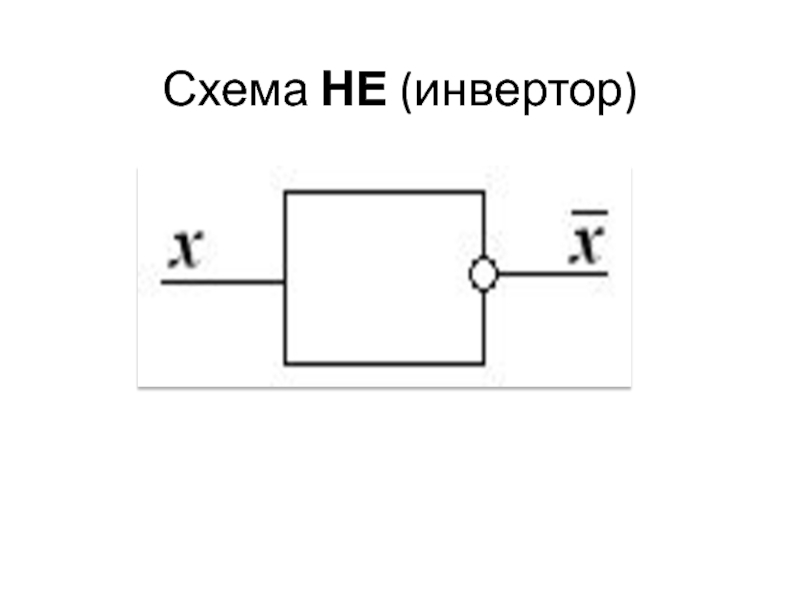
Обозначение логических элементов.
Слайд 34АРИСТОТЕЛЬ
(384-322 до н. э.)
Древнегреческий философ.
Основоположник формальной логики.
Слайд 35ЛЕЙБНИЦ Готфрид Вильгельм
(1646 — 1716)
Немецкий математик, физик и
философ.
Заложил основы математической логики.
Слайд 36ДЖОРДЖ БУЛЬ
(1815 —1864)
Английский математик и логик.
Сегодня идеи Буля используются во
всех современных цифровых устройствах.
Слайд 37Логическое высказывание повествовательное предложение, о котором можно сказать, истинно оно
или ложно.
Истина=1
Ложь=0
А: «дважды два равно четырем» истинно А=1,
В: «три больше
пяти» всегда есть ЛОЖЬ В=0.
Слайд 38Типы высказываний:
Простое –
никакая его часть сама не является высказыванием.
Составное
(сложное) –
состоит из простых высказываний.
Слайд 39Составляющие логического высказывания
Субъект, S -
понятие о предмете мысли
Предикат,
P -
понятие о свойствах и отношениях предмета мысли.
Субъект и
предикат - термины суждения.
Связка
отношения между субъектом и предикатом (выражается «есть», «не есть», «является», «состоит» и т.д.)
«Компьютер состоит из процессора, памяти и внешних устройств»
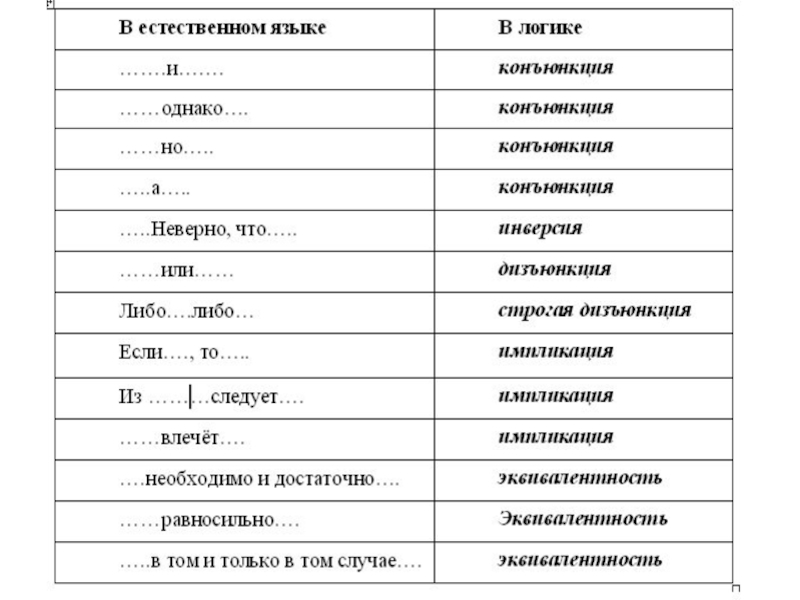
Слайд 40Логические операции:
Отрицание
Конъюнкция
Дизъюнкция
Строгая дизъюнкция
Импликация
Эквиваленция
Слайд 41Отрицание
(NOT, не, не верно, что)
Обозначения: ¬А; Ā
Инверсия высказывания истинна,
когда высказывание ложно, и ложна, когда высказывание истинно.
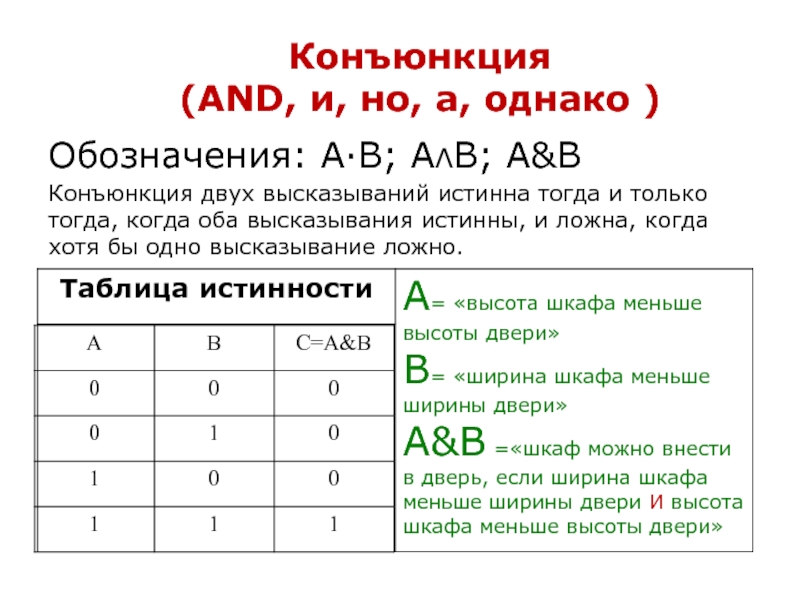
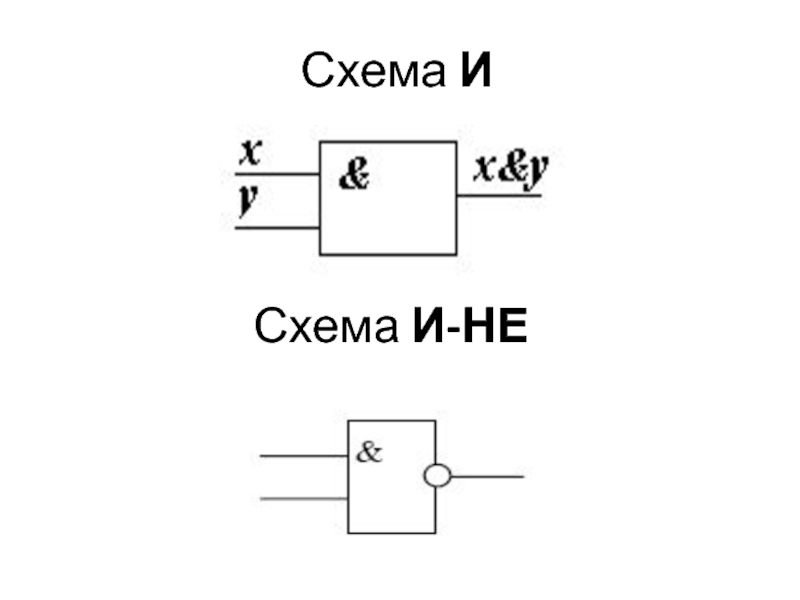
Слайд 42Обозначения: А·В; АΛВ; А&В
Конъюнкция двух высказываний истинна тогда и только
тогда, когда оба высказывания истинны, и ложна, когда хотя бы
одно высказывание ложно.
Конъюнкция
(AND, и, но, а, однако )
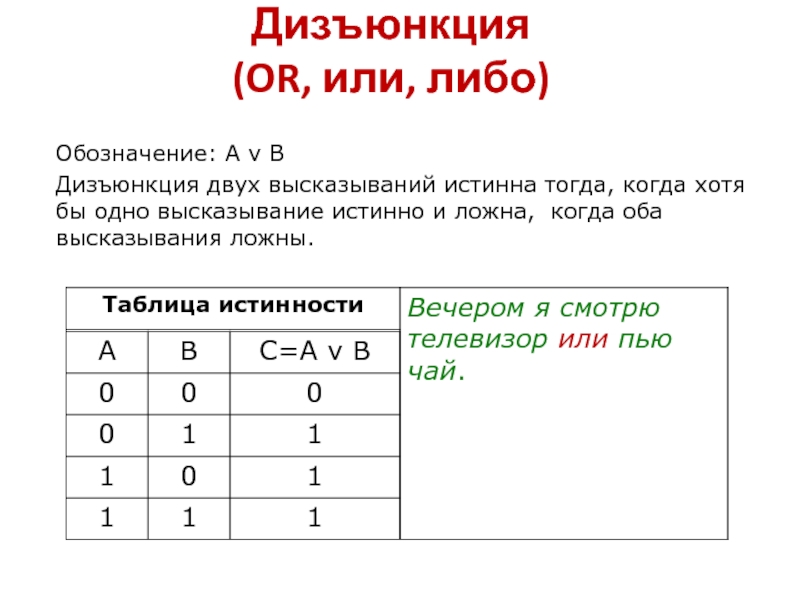
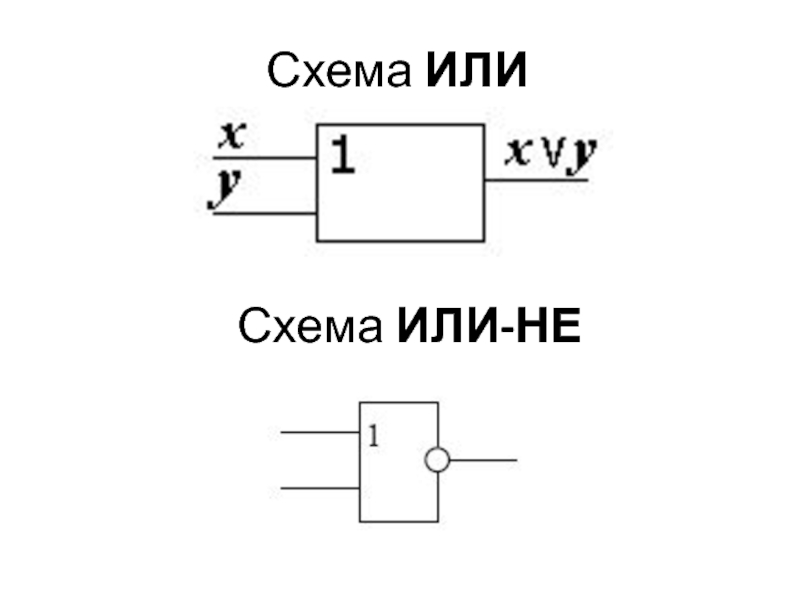
Слайд 43Дизъюнкция
(OR, или, либо)
Обозначение: А v В
Дизъюнкция двух высказываний истинна
тогда, когда хотя бы одно высказывание истинно и ложна, когда
оба высказывания ложны.
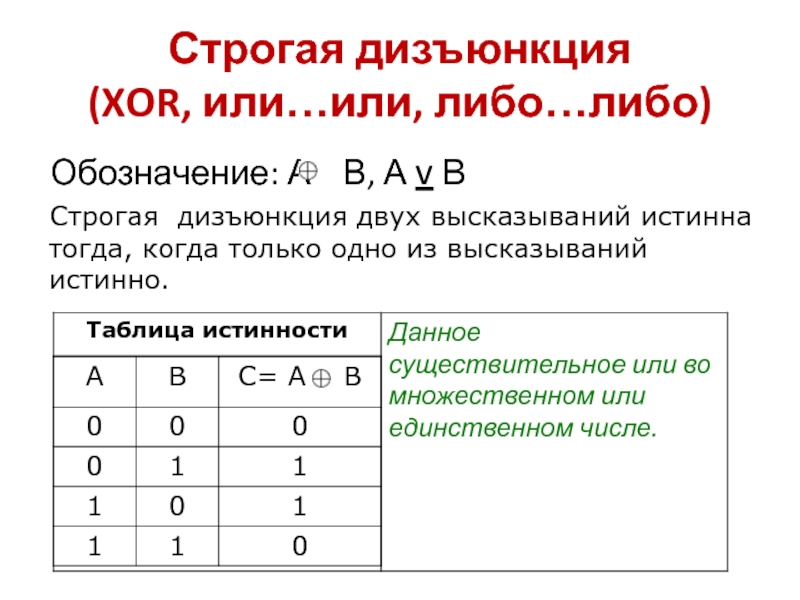
Слайд 44Строгая дизъюнкция
(XOR, или…или, либо…либо)
Обозначение: А В, А v
В
Строгая дизъюнкция двух высказываний истинна тогда, когда только одно из
высказываний истинно.
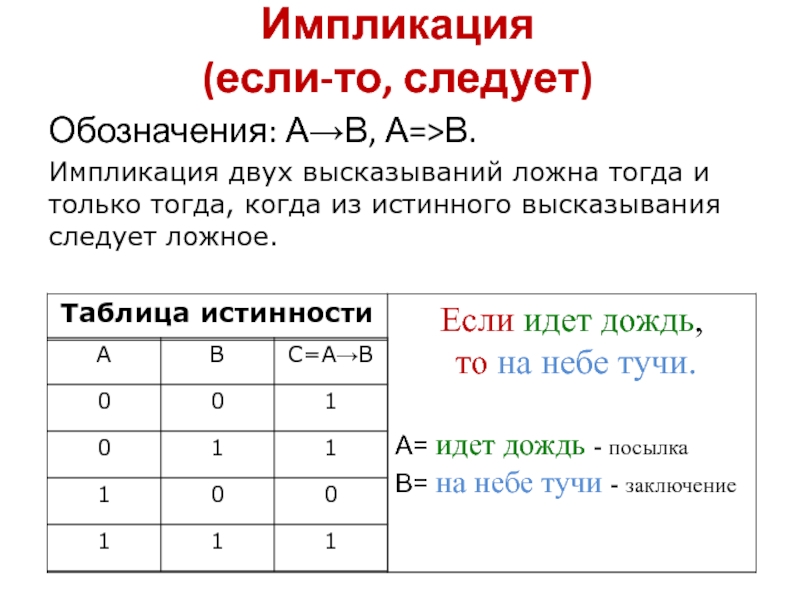
Слайд 45Импликация
(если-то, следует)
Обозначения: А→В, А=>В.
Импликация двух высказываний ложна тогда и только
тогда, когда из истинного высказывания следует ложное.
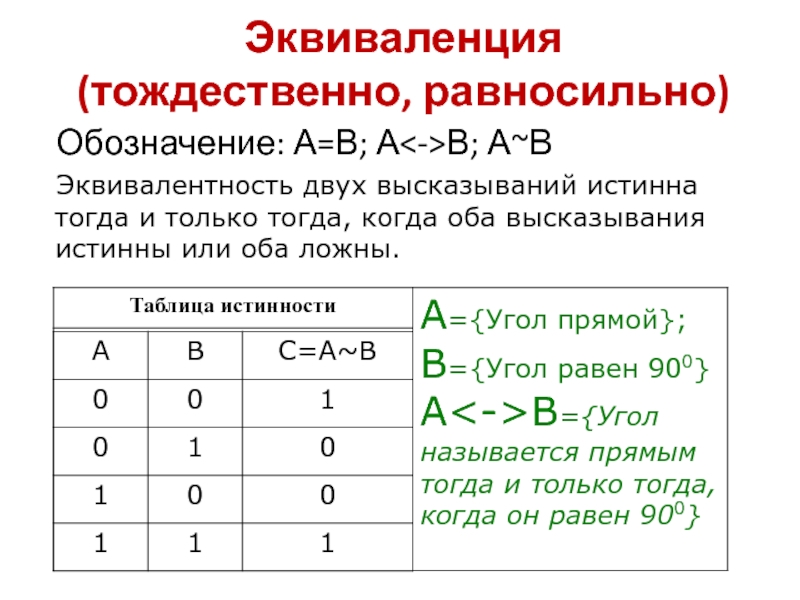
Слайд 46Эквиваленция
(тождественно, равносильно)
Обозначение: А=В; АВ; А~В
Эквивалентность двух высказываний истинна тогда и
только тогда, когда оба высказывания истинны или оба ложны.
Слайд 47Приоритет операций:
операции в скобках;
отрицание;
конъюнкция и дизъюнкция (слева направо);
импликация;
эквиваленция.
С = ((
A v В) -> В) v А
Слайд 49В зале №1 идет лекция по психологии или философии.
У пациента
ушиб или растяжение.
Аня отличница, но плохая спортсменка.
Если пожелтели листья, то
пришла осень.
Чтобы перейти на следующий курс достаточно сдать сессию на тройки.
Слайд 50Система аксиом, законы алгебры логики.
x = 0, если x
1.
x = 1, если x 0.
1 1 =
1 0 0 = 0
0 0 = 0 1 1 = 1
0 1 = 1 0 = 1 1 0 = 0 1 = 0
Слайд 51С помощью аксиом можно получить ряд тождеств:
Слайд 52законы алгебры логики:
переместительный (или коммутативный)
сочетательный (или ассоциативный)
Слайд 53распределительный (или дистрибутивный)
двойственности (или де Моргана)
двойного отрицания