Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛЕКЦИЯ №5
Содержание
- 1. ЛЕКЦИЯ №5
- 2. Раздел «Аналитическая геометрия на
- 3. Прямая на плоскостиОсновные уравнения прямой на плоскости1.
- 4. Прямая на плоскости. Основные уравнения4. Уравнение прямой,
- 5. Прямая на плоскости. Основные уравнения7. Уравнение прямой,
- 6. Задачи на составление уравнений прямой , определение
- 7. 2. Составить уравнение прямой, проходящей через данную
- 8. 3. Составить уравнение прямой, проходящей через точку
- 9. 4. Составить уравнение прямой, проходящей через точкуперпендикулярно
- 10. 5. Составить уравнение прямой, проходящей через точкуперпендикулярно
- 11. 6. Составить уравнение прямой, проходящей через точку
- 12. Взаимное расположение прямых на плоскостиЗадачи на взаимное
- 13. Нахождение угла между прямыми1. Если прямые заданы
- 14. Проверка условий параллельности и перпендикулярности прямых1. Условия
- 15. 1. Найти угол между прямымииИз уравнения первой
- 16. Кривые 2-го порядка Общее уравнение прямой
- 17. 1. Окружность Определение. Окружностью называется
- 18. Построение окружностей 1. Построить окружность
- 19. Построить окружность Каноническое
- 20. 2. Эллипс Определение. Эллипсом называется множество
- 21. Разновидности эллипсаУравнение эллипса со смещенным центром- центр
- 22. Построение эллипса1. Построить эллипс Центр эллипса Для
- 23. 2. Построить эллипсДля получения канонического уравнения делаем
- 24. 3. Построить кривую1.2. 4.5.Таким образом, центр эллипса
- 25. 4. Построить кривуюДанное уравнение определяет эллипс, так
- 26. 3. ГиперболаОпределение. Гиперболой называется множество точек плоскости,
- 27. Построение гиперболыДля построения
- 28. Виды гиперболРассмотрим другие виды гиперболСопряженная гипербола действительная
- 29. Рассмотрим примеры построения гипербол1. Построить гиперболуцентр гиперболыдействительная полуосьмнимая полуосьрасстояние между фокусами
- 30. 2. Построить кривуюВозведем в квадрат обе части
- 31. 3. Построить кривуюДанное уравнение определяет гиперболу (знаки
- 32. 4. ПараболаОпределение. Параболой называется множество точек плоскости,
- 33. Парабола со смещенной вершинойПарабола
- 34. Построение параболДля построения параболы нужно знать:Координаты вершины
- 35. 1. Построить параболуДанное уравнение является каноническим уравнением
- 36. 2. Построить кривуювершина параболыОсь симметрии параболы OX,
- 37. 3. Построить кривуюПреобразуем уравнениеУравнение определяет параболу. Сравнивая
- 38. 4. Построить параболуВ уравнении отсутствует квадрат переменной
- 39. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2 Раздел «Аналитическая геометрия на плоскости» курса «Высшая
математика» включает две основные темы:
Слайд 3Прямая на плоскости
Основные уравнения прямой на плоскости
1. Уравнение прямой, проходящей
через заданную точку
перпендикулярнозаданному вектору
2. Общее уравнение прямой
- вектор нормали
3. Уравнение прямой « в отрезках»
Слайд 4Прямая на плоскости. Основные уравнения
4. Уравнение прямой, проходящей через заданную
точку параллельно заданному вектору
- каноническое уравнение
- направляющий вектор
5. Параметрические уравнения
6. Уравнение прямой, проходящей через две заданные точки
и
Слайд 5Прямая на плоскости. Основные уравнения
7. Уравнение прямой, проходящей через заданную
точку с заданным
угловым коэффициентомУгловой коэффициент - это тангенс угла наклона прямой.
Угол отсчитывается от положительного направления оси OX
8. Уравнение прямой с угловым
коэффициентом
Слайд 6Задачи на составление уравнений прямой , определение параметров уравнений
1. Составить
уравнение прямой, проходящей через точку
параллельно прямой
Решение.
Нам задано уравнение прямой
общего вида-вектор нормали
Сравнивая с заданным уравнением, получаем координаты
вектора нормали Так как все параллельные прямые
можно охарактеризовать одним вектором нормали, то можно составить
уравнение параллельной прямой, проходящей через данную
в условии точку. За основу берем уравнение
-направляющий вектор
Найдем угловой коэффициент
. Построить прямую.
Слайд 72. Составить уравнение прямой, проходящей через данную точку
параллельно прямой
Из канонического уравнения
заданной прямой можно определить ее направляющий вектор
Поскольку для всех параллельных прямых можно взять один и тот же направляющий вектор, то берем за основу каноническое уравнение
и подставляем в него координаты точки
и направляющего вектора
Это уравнение можно преобразовать к уравнению
общего вида и к уравнению с угловым коэффициентом
угловой коэффициент
- вектор нормали
Слайд 83. Составить уравнение прямой, проходящей через точку
параллельно прямой
.
В данном случае
прямая задана уравнением с известным угловым коэффициентом y=kx+b. K=3
Все параллельные прямые имеют один угловой коэффициент.
Т.о. нам известна точка на прямой и угловой коэффициент.
Берем уравнение
Записав уравнение в виде
, определим вектор нормали
и направляющий вектор
Для построения прямой используем таблицу
Слайд 94. Составить уравнение прямой, проходящей через точку
перпендикулярно прямой
Из рисунка видно,
что вектор
нормали известной прямой
является направляющим для
искомой прямой, поэтому
используем каноническое уравнение
Таким образом, получили общее уравнение прямой, из которого
определяем вектор нормали
Из канонического уравнения можно перейти к уравнению
с угловым коэффициентом
Слайд 105. Составить уравнение прямой, проходящей через точку
перпендикулярно прямой
Из рисунка видно,
что направляющий вектор известной прямой является вектором нормали для искомой
прямой, поэтомуиспользуем уравнение прямой с известной точкой и вектором нормали
Прямая задана параметрическими
уравнениями, из которых найдем
направляющий вектор
Получили общее уравнение прямой, из которого
,
Записав уравнение в виде
найдем угловой коэффициент
,
Слайд 116. Составить уравнение прямой, проходящей через точку
перпендикулярно прямой
Из уравнения
заданной прямой можно взять угловой коэффициент
Из условия перпендикулярности прямых
можно найти
угловой коэффициент перпендикулярной прямойТеперь берем уравнение прямой с угловым коэффициентом и
подставляем координаты точки и значение углового коэффициента
Или
- общее уравнение
,
Слайд 12Взаимное расположение прямых на плоскости
Задачи на взаимное расположение прямых включают
слежующие
вопросы:
Нахождение точки пересечения.
Нахождение угла между прямыми
Проверка условий параллельности и перпендикулярности
прямыхДля нахождения точки пересечения нужно решить систему,
составленную из уравнений этих прямых, например
Систему можно решить методом Крамера
Точка пересечения
Слайд 13Нахождение угла между прямыми
1. Если прямые заданы общими уравнениями, то
угол между прямыми – это угол между векторами нормалей и
используется формула косинуса угла между векторами 2. Если прямые заданы каноническими уравнениями, то угол между
прямыми – это угол между направляющими векторами
3. Если прямые заданы угловыми коэффициентами, то находят тангенс угла
Слайд 14Проверка условий параллельности и перпендикулярности прямых
1. Условия параллельности прямых
2. Условия
перпендикулярности прямых
Расстояние от точки
до прямойДля нахождения расстояния от точки до прямой нужно координаты точки
Подставить в левую часть уравнения прямой, разделить на длину
вектора нормали и полученное значение взять по абсолютной величине.
Уравнение прямой должно быть приведены к общему виду
Слайд 151. Найти угол между прямыми
и
Из уравнения первой прямой определяем вектор
нормали
Из уравнения второй прямой находим направляющий вектор
Тогда вектор нормали этой
прямойИспользуем формулу
2. Найти расстояние от точки до прямой
Приведем сначала уравнение прямой к общему виду
или
. Теперь можно использовать формулу
Слайд 16Кривые 2-го порядка
Общее уравнение прямой на плоскости –
есть уравнение линейное относительно переменных и
Уравнение кривой
2-го порядкаквадратичная часть
линейная часть
В дальнейшем будем рассматривать уравнения кривых,
в которых отсутствует произведение
.
К кривым 2-го порядка относятся :
окружность, эллипс, гипербола и парабола.
Основная задача состоит в умении по уравнению определить
тип кривой, привести само уравнение к каноническому
виду и построить кривую в системе координат.
Слайд 171. Окружность
Определение. Окружностью называется множество точек плоскости,
равноудаленных от одной точки, называемой центром
Уравнение окружности со смещенным центром
Уравнение окружности с центром в начале координат
В уравнение окружности входят квадраты переменных,
причем коэффициенты при квадратах и знаки
при них одинаковые.
!
Слайд 18Построение окружностей
1. Построить окружность
2. Построить окружность
3. Построить окружность
Слайд 19 Построить окружность
Каноническое уравнение
Формула квадрата суммы
и разности двух чисел
1.
2.
3.
4.
5.
6.
центр окружности,
радиус окружности
Слайд 202. Эллипс
Определение. Эллипсом называется множество точек плоскости, сумма
расстояний которых до двух данных точек, называемых фокусами , есть
величина постоянная, равная длине большой оси .Каноническое уравнение эллипса
причем
вершины эллипса
фокусы эллипса
большая ось эллипса
малая ось эллипса
фокусное расстояние
В уравнение эллипса входят квадраты переменных,
причем знаки при квадратах одинаковые, а коэффициенты
при квадратах разные.
!
Слайд 21Разновидности эллипса
Уравнение эллипса со смещенным центром
- центр эллипса
Если в уравнении
эллипса
, то большой осью будет ось
, фокусы эллипса будут
лежать на этой оси и связь
между параметрами эллипса
будет такой:
.
.
Слайд 22Построение эллипса
1. Построить эллипс
Центр эллипса
Для построения эллипса нужно
знать координаты центра и
размеры полуосей и
Полуоси
Расстояние
между фокусами, т.е.
Можно найти площадь фигуры, ограниченной эллипсом по формуле
Для данного примера получим
.
.
Слайд 232. Построить эллипс
Для получения канонического уравнения делаем некоторые
преобразования:
Делим все члены
уравнения на 45, так чтобы получит единицу
в правой части
уравнения2) Убираем в знаменатель коэффициенты из числителей
Получили уравнение эллипса, из которого определяем положение
центра и размеры полуосей
- центр эллипса
- полуоси
3) Строим эллипс
Слайд 243. Построить кривую
1.
2.
4.
5.
Таким образом, центр эллипса имеет координаты
Полуоси эллипса
При
построении необходимо учесть, что уравнение определяет
Только правую половинку эллипса,
так как по условию имеем, т.е.
3.
Слайд 254. Построить кривую
Данное уравнение определяет эллипс, так как есть квадраты
переменных, знаки при которых одинаковые, а коэффициенты
различные. Кроме того, наличие
линейной части уравнения означает, что центр эллипса смещен от начала координат.
Приводим уравнение к каноническому виду
Используем прием выделения полного квадрата согласно формуле
1.
2.
3.
4.
5.
6.
центр
полуоси
,
,
Слайд 263. Гипербола
Определение. Гиперболой называется множество точек плоскости, разность расстояний которых
до двух данных точек, называемых фокусами ,по абсолютной есть величина
постоянная, равная длине действительной оси .действительная полуось
мнимая полуось
Каноническое уравнение гиперболы с центром в начале координат
В этом случае
Фокусы гиперболы всегда лежат на действительной оси.
Связь между параметрами гиперболы определяется соотношением
В уравнение гиперболы входят квадраты переменных, причем знаки при квадратах разные.
!
Асимптоты гиперболы – это прямые к которым гипербола неограниченно приближается на бесконечности.
Слайд 27 Построение гиперболы
Для построения гиперболы удобно пользоваться
вспомогательными
построениями.
1. В системе координат строим прямоугольник с размерами
на осях OX
и OY соответственно.2. Проводим диагонали этого прямоугольника.
Уравнения диагоналей – это уравнения асимптот гиперболы
3. На действительной оси отмечаем вершины гиперболы и от них
ведем ветви гиперболы к асимптотам.
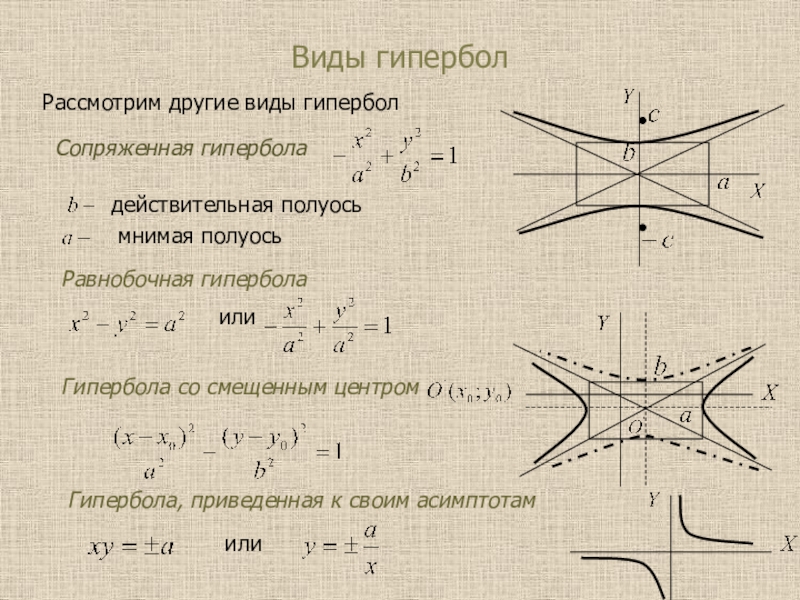
Слайд 28Виды гипербол
Рассмотрим другие виды гипербол
Сопряженная гипербола
действительная полуось
мнимая полуось
Равнобочная гипербола
или
Гипербола со смещенным центром
Гипербола, приведенная к своим асимптотам
или
Слайд 29Рассмотрим примеры построения гипербол
1. Построить гиперболу
центр гиперболы
действительная полуось
мнимая полуось
расстояние между
фокусами
Слайд 302. Построить кривую
Возведем в квадрат обе части уравнения
Собираем квадраты переменных
в левую часть уравнения
Данное уравнение определяет гиперболу, так как знаки
при квадратахпеременных разные. Кроме того, данная гипербола
является сопряженной и равнобочной
Можно записать уравнение в виде
мнимая полуось
действительная
полуось
Оставляем только нижнюю ветвь гиперболы, так как по условию
Слайд 313. Построить кривую
Данное уравнение определяет гиперболу (знаки при квадратах
переменных
различные) со смещенным центром (есть линейная часть)
Приведем уравнение к каноническому
видуцентр гиперболы
действительная полуось
мнимая полуось
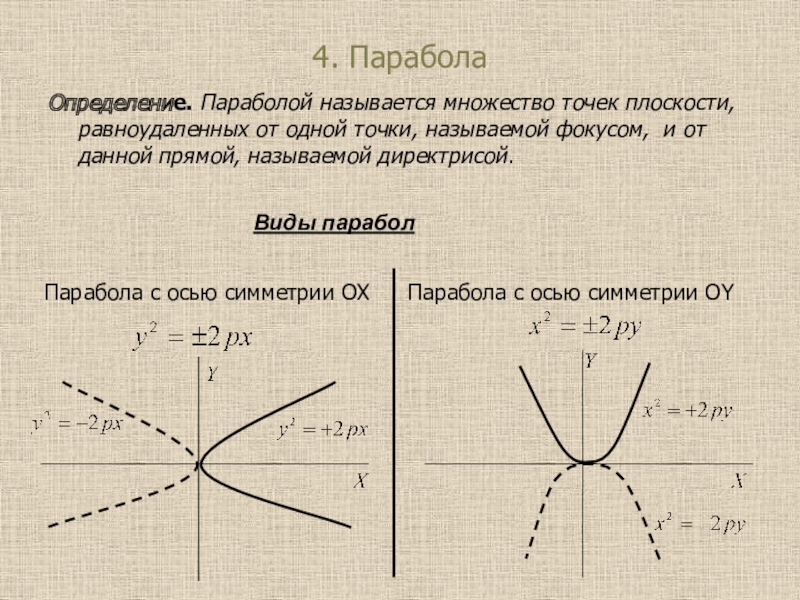
Слайд 324. Парабола
Определение. Параболой называется множество точек плоскости, равноудаленных от одной
точки, называемой фокусом, и от данной прямой, называемой директрисой.
Виды парабол
Парабола
с осью симметрии OXПарабола c осью симметрии OY
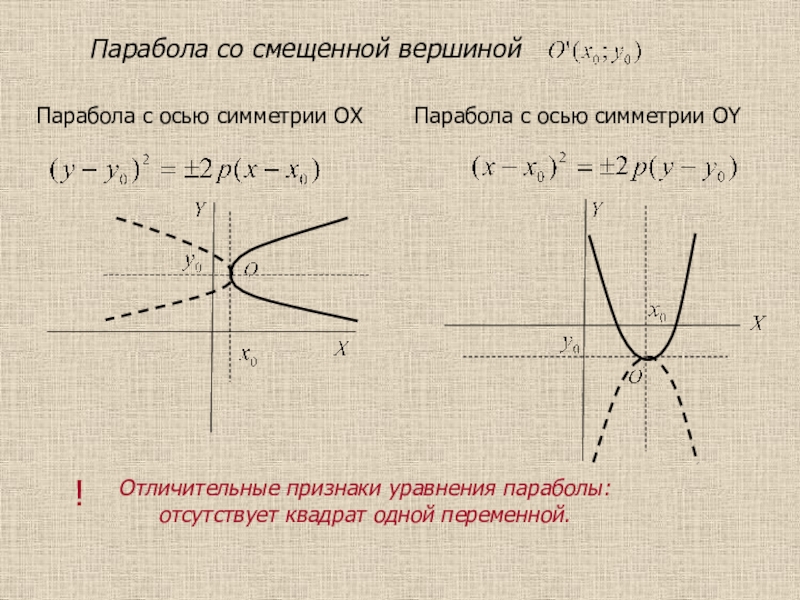
Слайд 33 Парабола со смещенной вершиной
Парабола с осью симметрии
OX
Парабола c осью симметрии OY
Отличительные признаки уравнения параболы:
отсутствует квадрат одной
переменной.!
Слайд 34Построение парабол
Для построения параболы нужно знать:
Координаты вершины
.
Ось симметрии параболы (определяется
по той переменно, квадрат которой отсутствует в уравнении)Направление ветвей (определяется по знаку : если в правой части канонического уравнения знак плюс, то ветви параболы идут в положительном направлении оси симметрии, если знак минус, то в отрицательном )
Параметр параболы определяется по коэффициенту при переменной, стоящей в каноническом уравнении в первой степени, и определяет «ширину» параболы. Знание параметра помогает более качественно получить начальный участок параболы.
Слайд 351. Построить параболу
Данное уравнение является каноническим уравнением параболы,
так как
отсутствует квадрат переменной . Поэтому осью
симметрии
параболы будет ось OX.Вершина параболы в точке
Ветви параболы направлены в положительном направлении оси OX,
так как в правой части уравнения знак “плюс”.
ширина параболы
параметр параболы
Слайд 362. Построить кривую
вершина параболы
Ось симметрии параболы OX, так как отсутствует
квадрат
переменной x
Ветви параболы направлены влево, так как в правой
части уравненияполучился знак “минус”
параметр параболы
Так как по условию , то уравнение определяет только
верхнюю ветвь параболы
Слайд 373. Построить кривую
Преобразуем уравнение
Уравнение определяет параболу. Сравнивая с уравнением
, определяем
координаты вершины
. Ось симметрии OY. Ветви направлены вниз.
параметр параболы
Слайд 384. Построить параболу
В уравнении отсутствует квадрат переменной y, поэтому оно
определяет параболу с осью симметрии OY.
Проведем преобразования уравнения, чтобы
привести его к каноническому видуили
вершина параболы
параметр параболы
Ветви параболы направлены вниз