Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №6 по курсу Машинная арифметика в рациональных чисел Москва, 2020
Содержание
- 1. Лекция №6 по курсу Машинная арифметика в рациональных чисел Москва, 2020
- 2. 8080, 8 разр, 2 МГц8086, 16 разр,
- 3. Особенности формата с плавающей точкойРезкая потеря точности
- 4. Нарушение законов алгебрыСчитаете с одной точностью и
- 5. ПРИМЕР ЗАДАЧИ, ИМЕЮЩЕЙ РЕЗКИЙ РОСТ ОШИБОК ОКРУГЛЕНИЯОбращение
- 6. Матрица ГильбертаДля матрицы 12 уже неверные результаты.Число
- 7. Модулярная арифметикаАмербаев В.М.МОДУЛЯ́РНАЯ АРИФМЕ́ТИКА (система остаточных классов),
- 8. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 9. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 10. ПРИНЦИПЫ РЕАЛИЗАЦИИ МОДУЛЯРНЫХ ВЫЧИСЛЕНИЙ
- 11. Модулярная арифметика с дробями
- 12. Вычисления с дробями Фарея в модулярной арифметике.
- 13. Пример 1 задачи, чувствительной к изменению шага
- 14. Пример 2 задачи, чувствительной к изменению шага интегрированияПростейшее дифференциальное уравнение Число обусловленности:
- 15. Скачать презентанцию
8080, 8 разр, 2 МГц8086, 16 разр, 4-10 МГцPentium, 32 разр, 60-233 МГцРост разрядности и тактовой частоты процессоров по годамГипотеза: Технологические трудности создания процессоров высокой разрядности
Слайды и текст этой презентации
Слайд 28080, 8 разр, 2 МГц
8086, 16 разр, 4-10 МГц
Pentium, 32
разр, 60-233 МГц
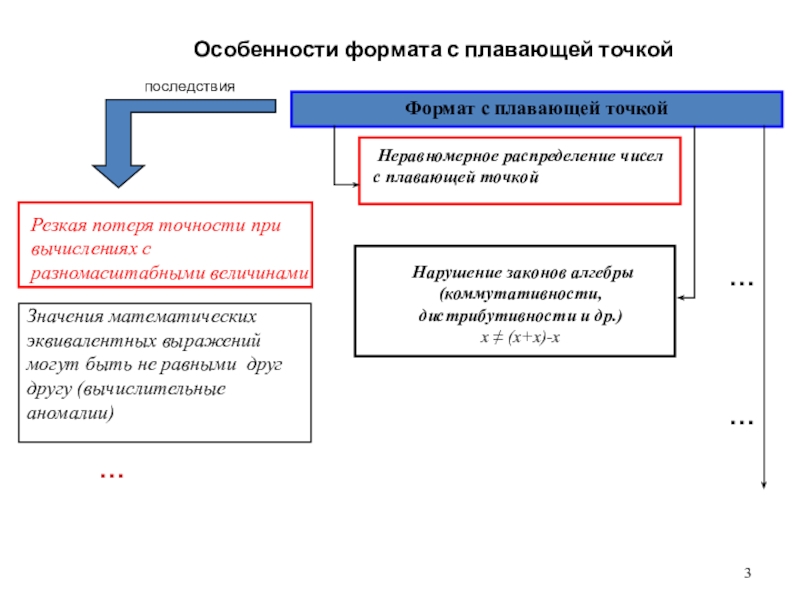
Технологические трудности создания процессоров высокой разрядности
Слайд 3Особенности формата с плавающей точкой
Резкая потеря точности при вычислениях с
разномасштабными величинами
Неравномерное распределение чисел
с плавающей точкой
Формат с плавающей
точкой
Нарушение законов алгебры (коммутативности, дистрибутивности и др.)
x ≠ (х+х)-х
…
Значения математических эквивалентных выражений могут быть не равными друг другу (вычислительные аномалии)
…
последствия
…
Слайд 4Нарушение законов алгебры
Считаете с одной точностью и с другой если
результаты примерно одинаковые, то вероятно задача решена правильно.
Слайд 5ПРИМЕР ЗАДАЧИ, ИМЕЮЩЕЙ РЕЗКИЙ РОСТ ОШИБОК ОКРУГЛЕНИЯ
Обращение матрицы Гильберта порядка
3
С точностью 2 знака после запятой
С точностью 3 знака
после запятой Макс. относ. погрешн. более 100%.
Макс. относ. погрешность более 100%.
Матрица Гильберта
Точный результат:
Слайд 6Матрица Гильберта
Для матрицы 12 уже неверные результаты.
Число обусловленности растёт экспоненциально!
Некоторые
матрицы имеют число обусловленности
пропорционально n или n2
Слайд 7Модулярная арифметика
Амербаев В.М.
МОДУЛЯ́РНАЯ АРИФМЕ́ТИКА (система остаточных классов), базируется на известном
в теории чисел частном виде отношения эквивалентности – понятии сравнения
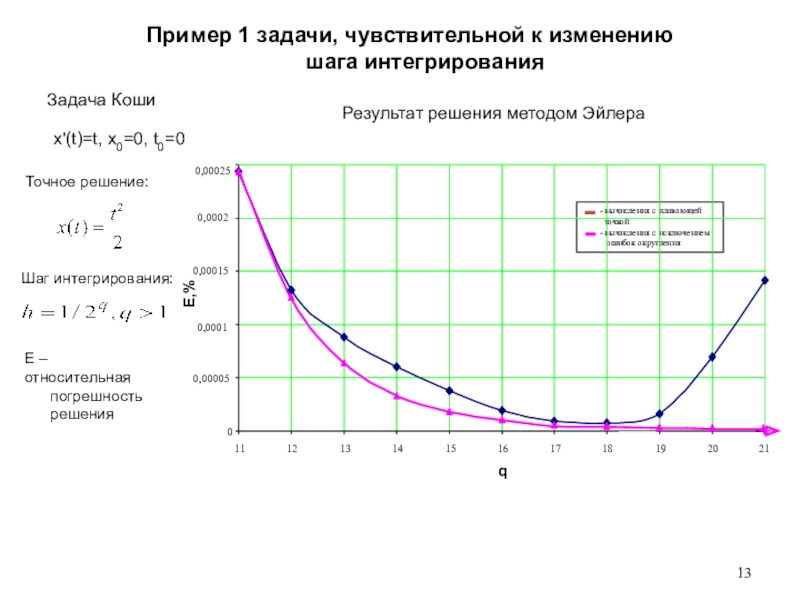
целого числа по натуральному модулю и возникающему при этой операции вычету. Для задания модулярной арифметики необходимо задать математические соотношения, позволяющие взаимнооднозначно отображать значение числовой величины в компоненты векторного представления и обратно, а также алгоритмы выполнения машинных операций над компонентами векторного модулярного представления.
Слайд 13Пример 1 задачи, чувствительной к изменению шага интегрирования
Задача Коши
x'(t)=t, x0=0,
t0=0
Шаг интегрирования:
E – относительная
погрешность
решенияРезультат решения методом Эйлера
0
0,00005
0,0001
0,00015
0,0002
0,00025
11
12
13
14
15
16
17
18
19
20
21
q
E,%
Точное решение:
Слайд 14Пример 2 задачи, чувствительной к изменению шага интегрирования
Простейшее дифференциальное уравнение
Число обусловленности:
