Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейный Гармонический осциллятор в квантовой механике
Содержание
- 1. Линейный Гармонический осциллятор в квантовой механике
- 2. изменяться только отдельными порциями. В квантовой механике
- 3. Здесь использовано соотношение k = mω2, ω
- 4. Рассмотрим теперь квантовый гармонический осциллятор. Переход от
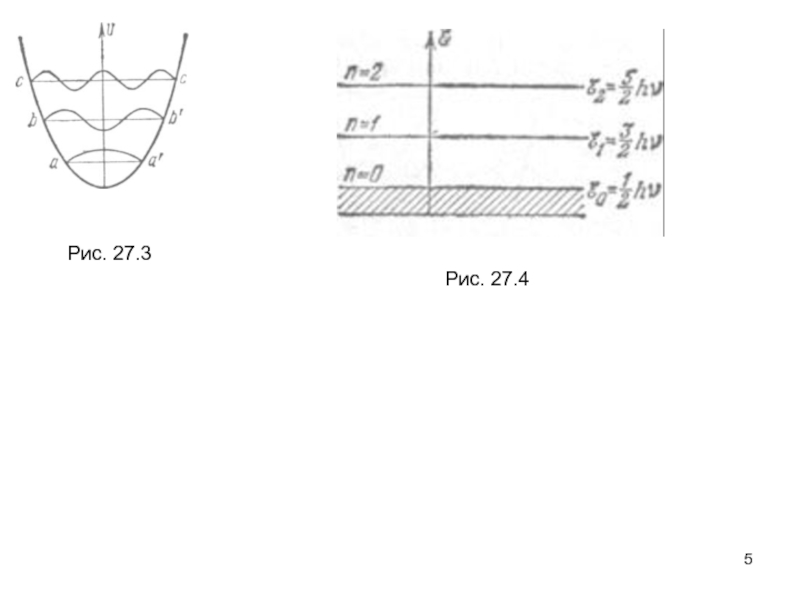
- 5. Рис. 27.3 Рис. 27.4
- 6. Таким образом, существует минимальное значение полной энергии
- 7. должны прекратиться тепловые колебания узлов решетки, на
- 8. Исключение составляет гелий, который является квантовой жидкостью
- 9. Найдем теперь все возможные значения полной энергии
- 10. Е = р2эфф /2m=
- 11. Из формулы (26.28) видно, что энергетические уровни
- 12. Строгое квантовомеханическое решение задачи о гармоническом осцилляторе
- 13. Слайд 13
- 14. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2изменяться только отдельными порциями. В квантовой механике идеи Планка получили
свое обоснование и развитие.
Вспомним прежде всего, как в классической физике
следует
рассматривать колебания гармонического осциллятора. На рис. 27.2
изображен график потенциальной энергии U осциллятора U= kx2/2.
На этом же графике показано значение полной энергии E частицы.
Точкам В и С на графике U(x) соответствуют наибольшие отклонения частицы от положения равновесия, когда скорость частицы обращается в нуль и ее полная энергияРис. 27.2
становится равной потенциальной:
при υ = 0 .
(26.19)
(26.20)
Слайд 3Здесь использовано соотношение k = mω2, ω = 2πν.
С классической
точки зрения совершенно очевидно, что частица при своих колебаниях не
может выйти за пределы области (-А, А).Амплитуда А колебаний осциллятора определяется запасом его
полной энергии Е:
(26.21)
Такой выход означал бы, что потенциальная энергия U становится большей, чем полная энергия E частицы: U > E, что соответствует бессмысленному выводу об отрицательной кинетической энергии, т. е. о мнимой скорости. Если mυ2/2 < 0, то υ — мнимая величина!
Слайд 4Рассмотрим теперь квантовый гармонический осциллятор. Переход от классического к квантовому рассмотрению
означает, что мы должны будем учесть волновые свойства частицы, запертой внутри потенциальной
ловушки, имеющей форму параболы (см. рис. 27.3). В квантовой механике соотношения неопределенностей приводят к принципиально новому результату: полная энергия гармонического осциллятора и амплитуда его колебаний не могут быть равны нулю. В самом деле, если частица «заперта» в области Δх ≈ А, то согласно П.Н. Δрх ≈ /А, и импульс р частицы не может быть равен нулю. Как показано ранее,При этом
полная энергия Е удовлетворяет соотношению
(26.22)
Сравнивая (26.22) с (26.20) и исключив амплитуду А, имеем
.
Слайд 6Таким образом, существует минимальное значение полной энергии гармонического осциллятора, равное
и
называемое нулевой энергией осциллятора.
(26.23)
Нулевая энергия осциллятора определяется только
его
собственной частотой v. Ее невозможно отнять у частицы никаким
охлаждением, она сохранилась бы и при температуре абсолютного
нуля. Нулевой энергии соответствуют некоторые «нулевые колебания» квантового осциллятора.Существование нулевой энергии подтверждено экспериментально в явлении рассеяния света кристаллами при сверхнизких температурах. Рассеяние света в кристаллах происходит на тепловых колебаниях, которые совершают атомы, молекулы или ионы, расположенные в узлах кристаллической решетки. С классической точки зрения интенсивность рассеянного света должна убывать до нуля с уменьшением температуры до нуля, ибо
Слайд 7должны прекратиться тепловые колебания узлов решетки, на которых происходит рассеяние
света. Опыты показали, что при уменьшении температуры интенсивность света, рассеянного
кристаллами, стремится к некоторому предельному значению, которое не убывает при дальнейшем охлаждении кристалла. Результаты опытов показали, что при Т→0 у частиц, расположенных в узлах решетки, сохраняются некоторые «нулевые колебания», на которых и происходит рассеяние света. «Нулевым колебаниям» соответствует нулевая энергия атомных осцилляторов.Наличие нулевой энергии является характерным признаком любой системы частиц, рассматриваемой в квантовой механике. При температурах, близких к абсолютному нулю, любое вещество находится в кристаллическом состоянии и его атомы (молекулы или ионы) ведут себя как некоторые колеблющиеся осцилляторы.
Слайд 8Исключение составляет гелий, который является квантовой жидкостью вплоть до абсолютного
нуля, если давление не превышает 2,53 МПа. Это объясняется, во-первых,
тем, что у гелия частота колебаний атомов достаточно велика, ибо мала масса атома . Поэтому у гелия нулевая энергия hv/2 имеет сравнительнобольшую величину. С другой стороны, силы взаимодействия между атомами гелия малы, ибо у них электронные оболочки с двумя электронами полностью «застроены». В итоге атомы гелия при Т→0 находятся в интенсивном движении, и гелий при относительно небольших давлениях остается жидким и при Т→0. Поскольку причиной этого является квантовый эффект
Слайд 9 Найдем теперь все возможные значения полной энергии квантового гармонического осциллятора.
Движение частицы в этом случае ограничено потенциальной кривой параболического типа
U = mω2х2/2 (рис. 26.3). Как и в случае частицы, «запертой» в прямоугольном ящике, наличие потенциальной ловушки параболического типа приводит к дискретному набору энергий частицы. Квантованные значения энергии осциллятора будут определяться тем, что на эффективной длине 2Aэфф = аа', b'b’, . . . укладывается нечетное число полуволн де Бройля.Рис. 26.3
Введем эффективную длину волны де Бройля:
, (26.24)
где рэфф — эффективный импульс, связанный с энергией так, как будто потенциальная ловушка отсутствует и движение совершенно свободно:
Слайд 10Е = р2эфф /2m= .
(26.25)
Из рис. 26.3 видно, что на эффективной
амплитуде Aэфф укладывается нечетное число четвертей эффективных длин волн де Бройля: (26.26)Подставив (26.26) в (26.20), получим
Е = (2n + 1 )2 mω2λ2 эфф/32. (26.27)
Перемножая (26.25) и (27.27), исключим λэфф и найдем дискретные энергетические уровни линейного гармонического осциллятора:
В квантовой механике при строгом подходе, основанном на решении уравнения Шредингера, получается следующее выражение для возможных энергий осциллятора:
E = (n + 1/2)hv, где n = 0,1,2,… (26.28)
Слайд 11Из формулы (26.28) видно, что энергетические уровни гармонического осциллятора представляют
собой систему равноотстоящих друг от друга значений энергии (рис. 26.4).
Грубый расчет, приведенный выше, привел к правильной зависимости энергии линейного гармонического осциллятора от его частоты v и к правильному характеру зависимости En от n.Рис. 26.4
Слайд 12Строгое квантовомеханическое решение задачи о гармоническом осцилляторе приводит еще к
одному существенному отличию от классического рассмотрения. Оказывается, что можно обнаружить
частицу за пределами дозволенной области ⏐x⏐≤ A, т. е. за точками С и В на рис. 26.2. Как нам известно, это означает пребывание частицы там, где ее полная энергия Е меньше потенциальной энергии. Однако благодаря волновым свойствам частиц и принципу неопределенностей обнаружение частицы за пределами классически дозволенной области оказывается возможным. Подробнее мы рассмотрим причину этого в следующем параграфе.http://portal.tpu.ru/departments/head/methodic/standart
Работы выпускные квалификационные, проекты и работы курсовые. Структура и правила оформления. СТО ТПУ 2.5.01-2006