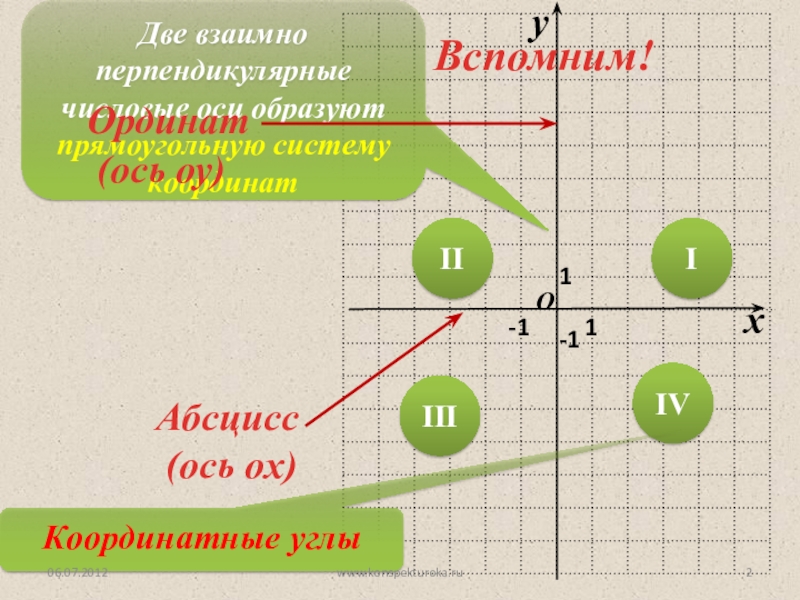
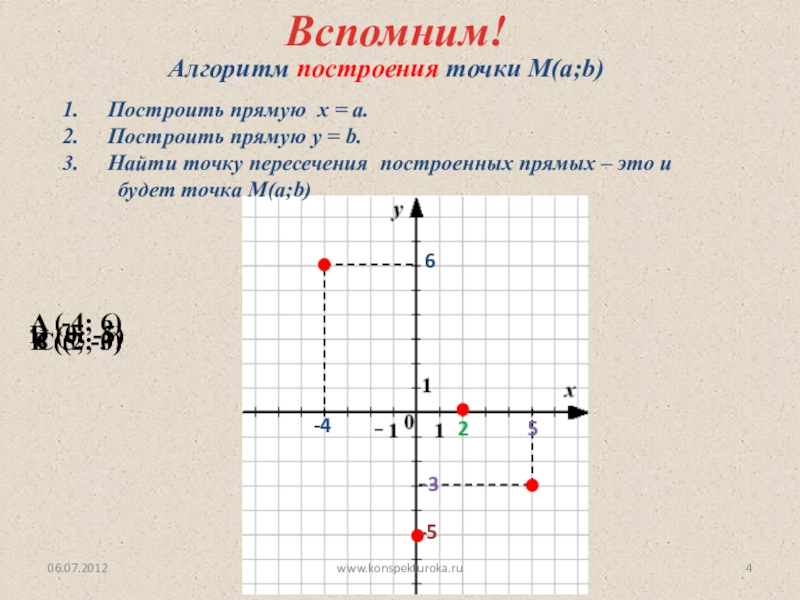
параллельную оси у,
и найти координату точки
пересечения этой прямой
с осью х – это и будет абсцисса точки.
2. Провести через точку
прямую, параллельную оси х,
и найти координату точки
пересечения этой прямой с осью
у - это и будет ордината точки.
А
В
С
М
В(2;5);
С(4;-5);
М(-5;-2);
А(-3;3)