Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Локализованные волны в фотонном кристалле: частотная дисперсия, керровская
Содержание
- 1. Локализованные волны в фотонном кристалле: частотная дисперсия, керровская
- 2. Слайд 2
- 3. Слайд 3
- 4. Реальные фотонные кристаллы (ФК)
- 5. Слайд 5
- 6. Фотонный кристалл и локализованная волнадефектный слой ФК = оптическая полость = резонатор Фабри-Перо
- 7. Локализованные волныOЧастотная дисперсияМеталл-диэлектрический нанокомпозитМногоуровневая квантовая системаКерровская нелинейностьОптическая
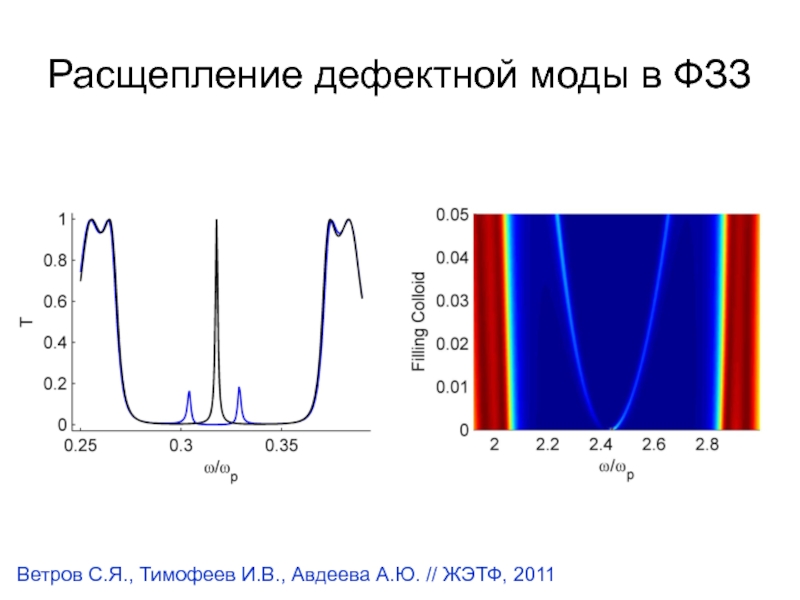
- 8. Расщепление дефектной моды в ФЗЗВетров С.Я., Тимофеев И.В., Авдеева А.Ю. // ЖЭТФ, 2011
- 9. Диэлектрическая проницаемость нанокомпозита определяется формулой Максвелла-Гарнетта, широко
- 10. Модель двумерного фотонного кристалла
- 11. Пространственное распределение интенсивности для частоты, соответствующей максимуму
- 12. Модифицированный метод плоских волнгдегдеБеликов А.В., Богданова М.В., Лозовик Ю.Е. // Мат Моделирование, 2007
- 13. Зонная структура двумерного ФК - усредненный
- 14. Спектр пропускания и зонная структура ФК
- 15. Оптическое таммовское состояниеТамм ЖЭТФ 1933Кавокин 2005Калитеевский 2007Виноградов УФН 2010Афиногенов 2013уравнение Шредингерауравнение Максвелла
- 16. Анизотропный нанокомпозит в качестве слоя фотонного кристаллаПродолговатые
- 17. db = 55 нм. da = 110 нмdb = 40 нм.da = 74 нм. Спектр
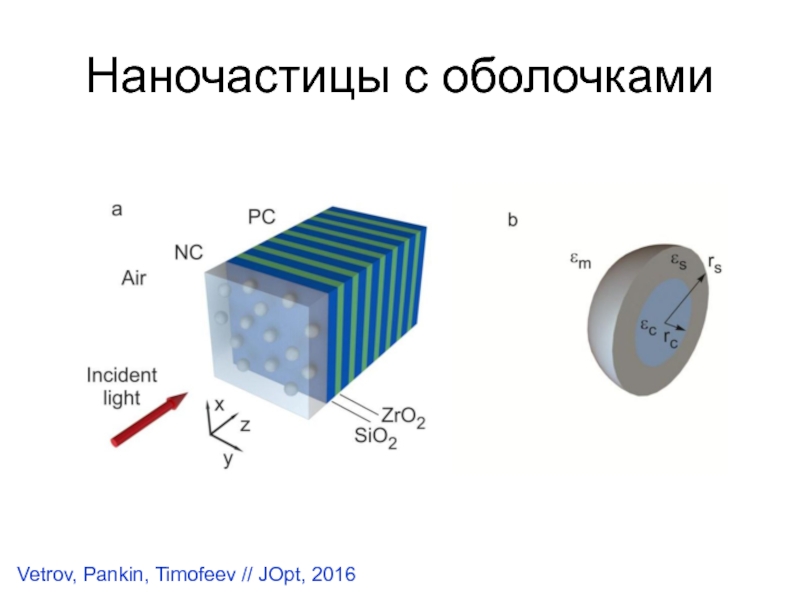
- 18. Наночастицы с оболочкамиVetrov, Pankin, Timofeev // JOpt, 2016
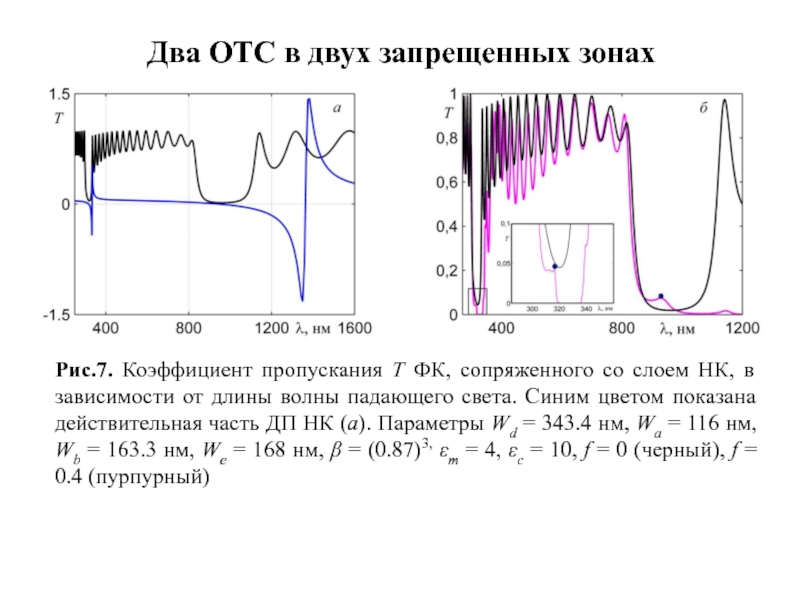
- 19. Рис.7. Коэффициент пропускания T ФК, сопряженного со
- 20. Локализованные волныЧастотная дисперсияМеталл-диэлектрический нанокомпозитМногоуровневая квантовая системаКерровская нелинейностьОптическая
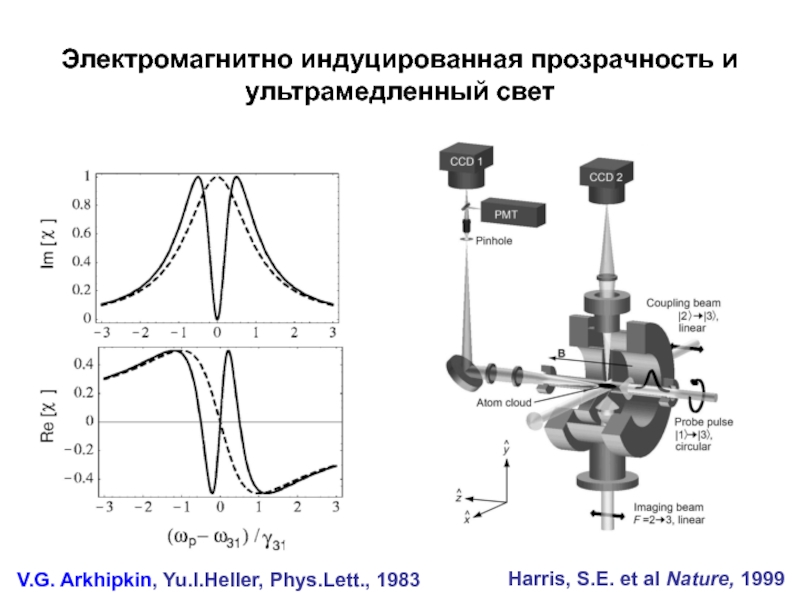
- 21. Электромагнитно индуцированная прозрачность и ультрамедленный светHarris, S.E. et al Nature, 1999V.G. Arkhipkin, Yu.I.Heller, Phys.Lett., 1983
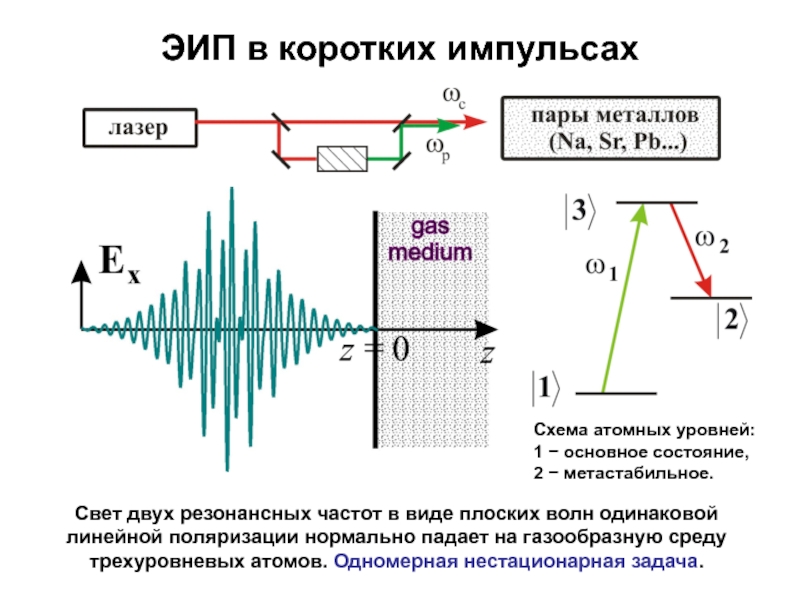
- 22. ЭИП в коротких импульсахСвет двух резонансных частот
- 23. ЭИП и замедление скорости импульсаабЗависимости нормированной частоты
- 24. Временная эволюция нормированных частот Раби импульсов на
- 25. ЭИП в дефекте ФКЛокализация поля в ФКДефектные
- 26. Локализованные волныЧастотная дисперсияМеталл-диэлектрический нанокомпозитМногоуровневая квантовая системаКерровская нелинейностьОптическая
- 27. Полностью оптический диодпропускает свет, отражает обратный светотличается
- 28. Свет в несимметричной средеКерровская нелинейность: Под действием
- 29. Распределение поля в средеz, мкм99,3%1,2%
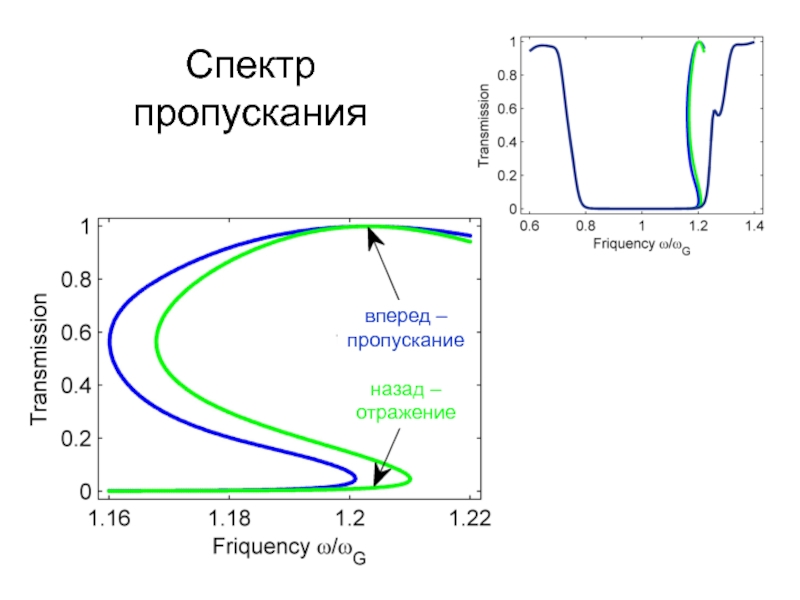
- 30. Спектр пропусканиявперед –пропусканиеназад – отражение
- 31. Распространение импульса через аподизованную структуруλ = 2.2 мкмλ = 1.2 мкм
- 32. Какой длительности должен быть импульс, чтобы поле можно было считать стационарным?Длительность импульса ~10-13 c
- 33. Распределение электрического и магнитного поля в слояхn
- 34. Ех , Ну непрерывны на границах раздела средТМ - метод
- 35. FDTD (the Finite-Difference Time-Domain Method) – метод конечных разностей во временной области
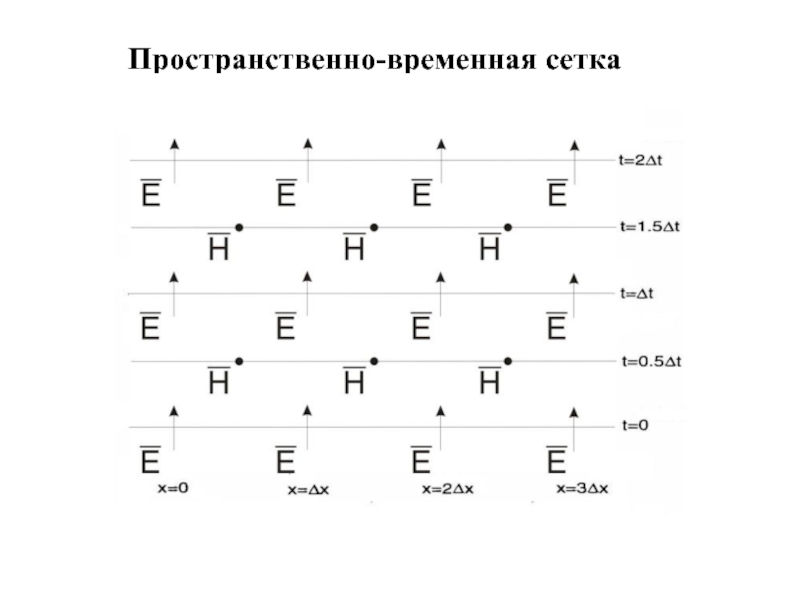
- 36. Пространственно-временная сетка
- 37. Сдвиг Гуса-Хенхен
- 38. Локализованные волныЧастотная дисперсияМеталл-диэлектрический нанокомпозитМногоуровневая квантовая системаКерровская нелинейностьОптическая
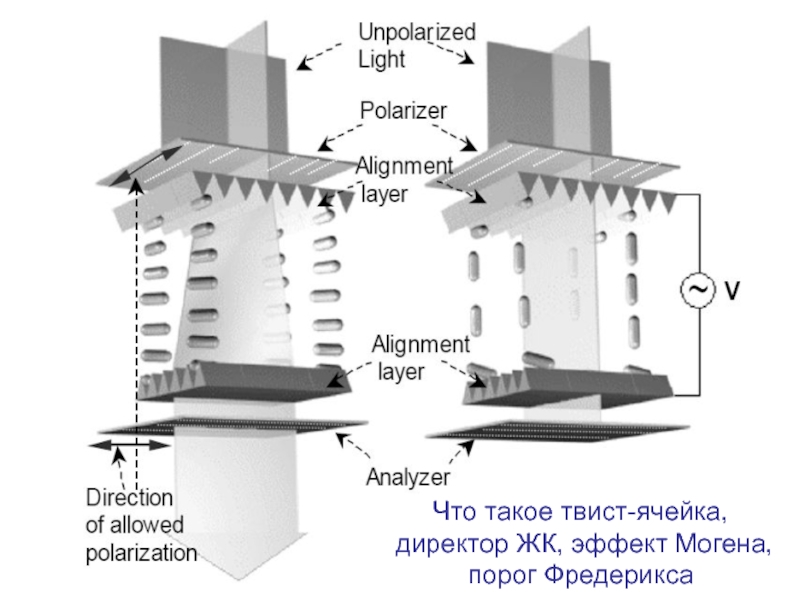
- 39. Что такое твист-ячейка, директор ЖК, эффект Могена, порог Фредерикса
- 40. Эксперимент: ЖК в ФКГуняков В.А., Мысливец С.А.,
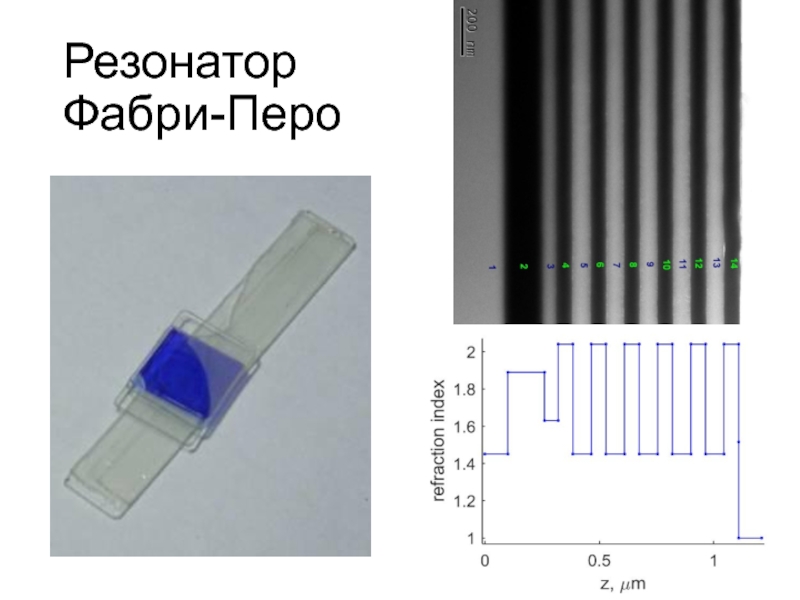
- 41. Резонатор Фабри-Перо
- 42. Расчетный спектр пропускания неполяризованного света в зависимости
- 43. Локализованные волныЧастотная дисперсияМеталл-диэлектрический нанокомпозитМногоуровневая квантовая системаКерровская нелинейностьОптическая
- 44. Твист-ячейка с наклонными граничными условиями. Гомеотропное и скрученное состоянияWu, Zou, Timofeev // Opt Express, 2011
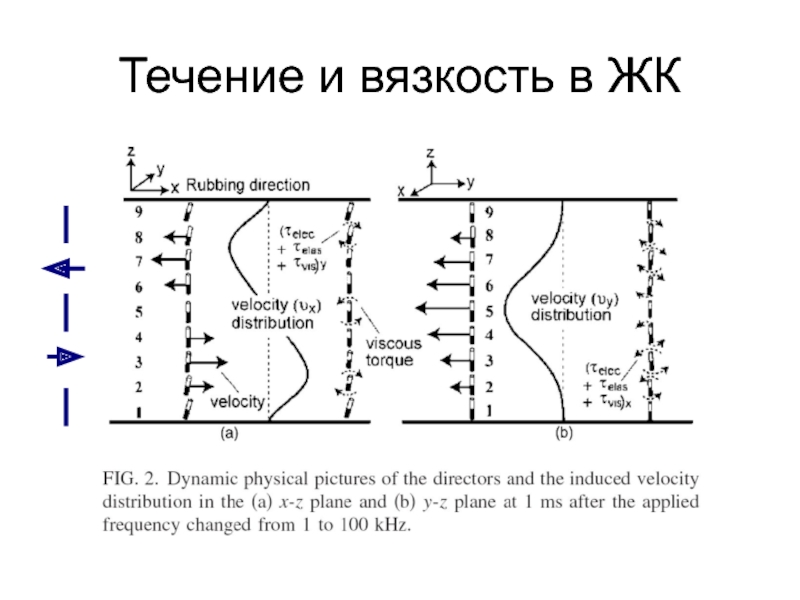
- 45. Течение и вязкость в ЖК
- 46. Метод расчета. Упругие силыгуковскийнаклонгуковскоескручиваниенаклонФермааналогия:луч в соленой водекатеноид мыльной пленки
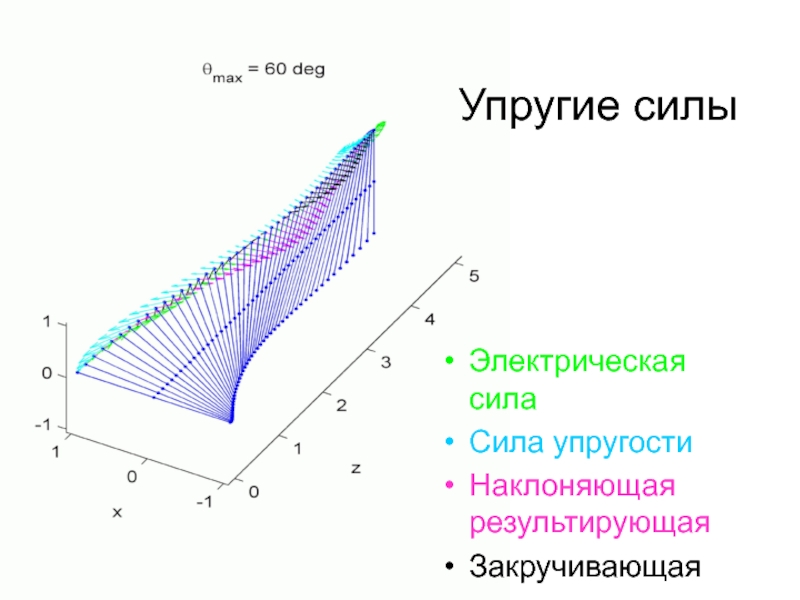
- 47. Электрическая силаСила упругостиНаклоняющая результирующаяЗакручивающаяУпругие силы
- 48. Расчет поля в анизотропной структуре. Матричная форма уравнений МаксвеллаBerreman D.W. // JOSA 1972
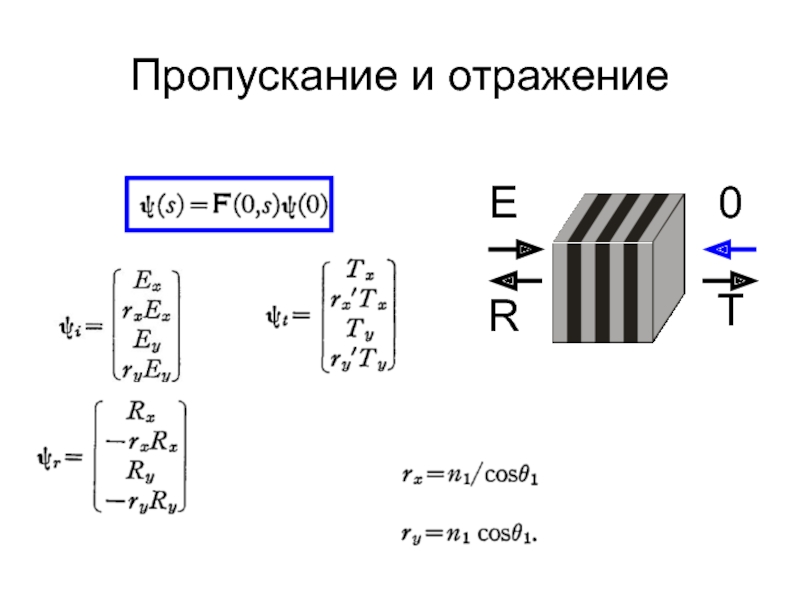
- 49. Пропускание и отражениеER0T
- 50. Локализованные волныЧастотная дисперсияМеталл-диэлектрический нанокомпозитМногоуровневая квантовая системаКерровская нелинейностьОптическая
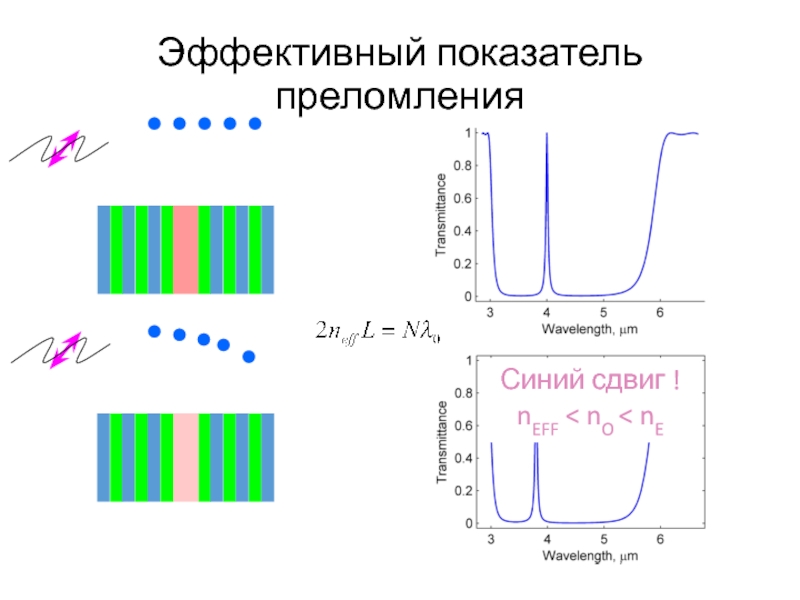
- 51. ?Синий сдвиг !nEFF < nO < nEЭффективный показатель преломления
- 52. Микрофотографии оптических текстур образца в геометрии параллельных
- 53. Спектральный сдвиг пиков пропусканияПоляризованный спектр а) и
- 54. Топологическая фотоника
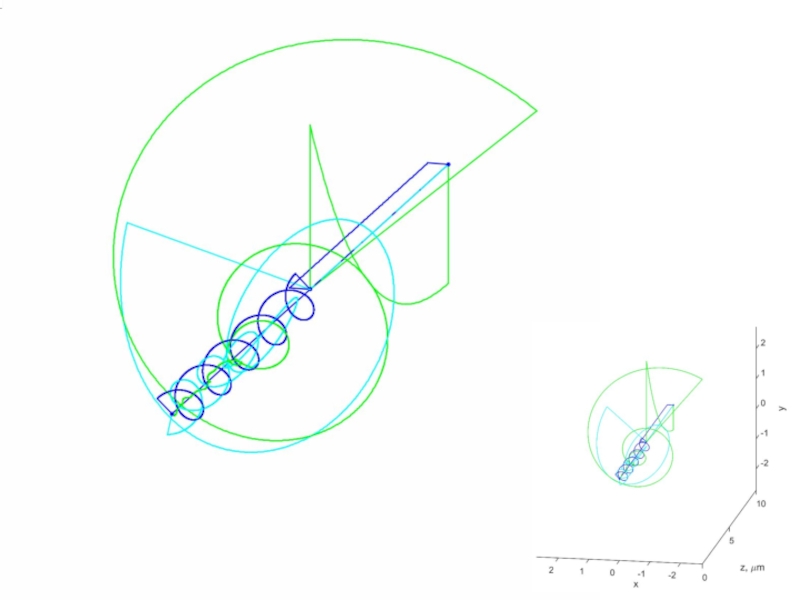
- 55. В каждой точке среды напряженность поляосциллирует по эллиптической траектории.
- 56. Собственная мода резонатора
- 57. Резонаторная модаl = 579.1 нм
- 58. Сферический избыток треугольника есть его площадьhttp://www.youtube.com/watch?v=jhULX60K-Vw
- 59. Локализованные волныЧастотная дисперсияМеталл-диэлектрический нанокомпозитМногоуровневая квантовая системаКерровская нелинейностьОптическая
- 60. Типы «зеркал»Полное внутреннее отражениеМеталлическое отражениеФотонно-кристаллическое отражениеЗеркально-симметричные фотонные
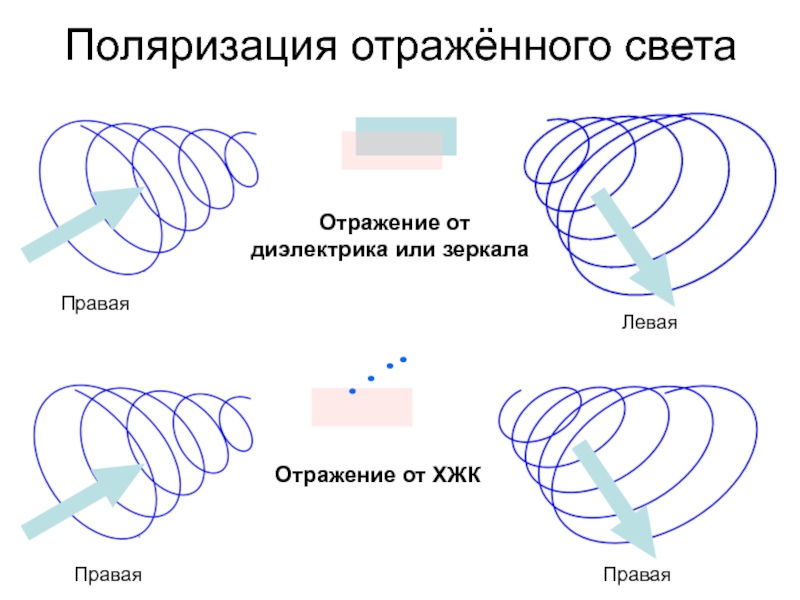
- 61. Отражение от ХЖКПоляризация отражённого света Отражение от диэлектрика или зеркалаПраваяЛеваяПраваяПравая
- 62. Холестерик-поглотительTimofeev et. al. // Opt Mat Ex 2013RХЖК
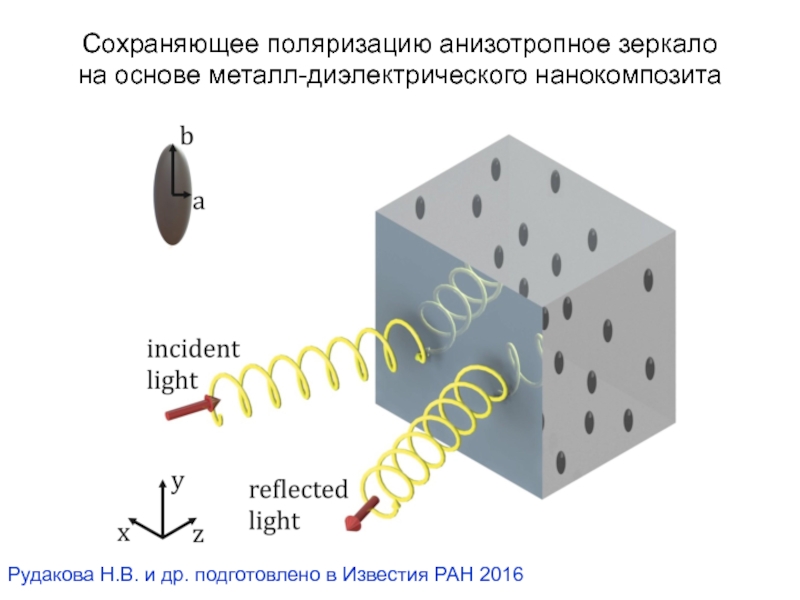
- 63. Сохраняющее поляризацию анизотропное зеркало на основе металл-диэлектрического
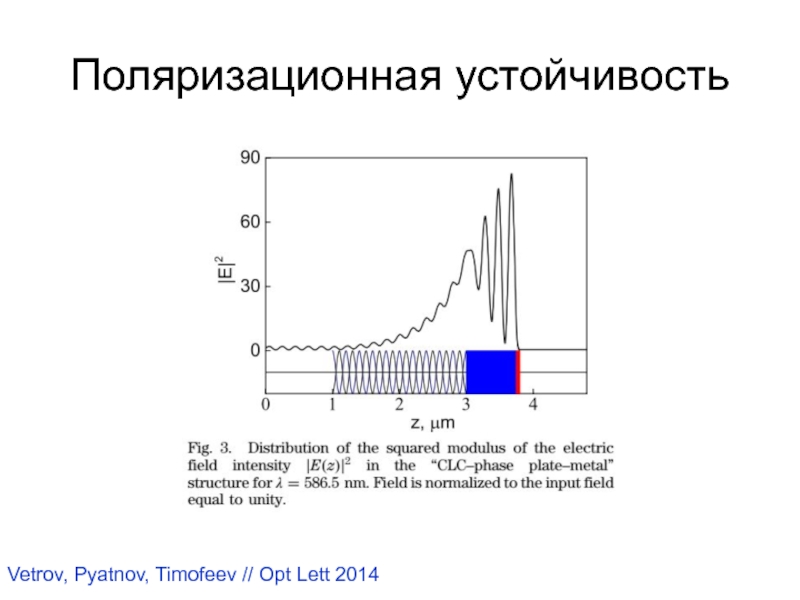
- 64. Поляризационная устойчивостьVetrov, Pyatnov, Timofeev // Opt Lett 2014
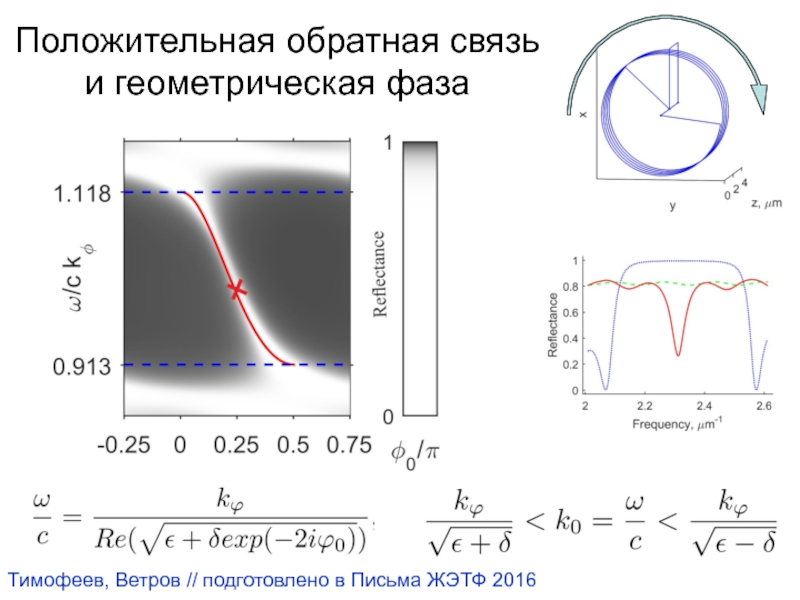
- 65. Положительная обратная связь и геометрическая фазаТимофеев, Ветров // подготовлено в Письма ЖЭТФ 2016
- 66. Сравнение локализации? ∼ ?? + ??
- 67. Слайд 67
- 68. Общее резюме
- 69. КоллегиАрхипкинВасилийГригорьевичВетровСтепанЯковлевичЗыряновВикторЯковлевичВей Ли,Тайвань,Тайнань
- 70. КоллегиГуняков Владимир АлексеевичСутормин Виталий СергеевичВьюнышевАндрейМихайловичРудаковаНаталья Викторовна
- 71. КоллегиБикбаевРашид ГельмединовичАвдееваАнастасияЮрьевнаПанкинПавелСергеевичПятновМаксимВладимирович
- 72. Творческие планыЭкспериментальная проверка спектральных сдвигов в холестерике
- 73. Методы исследованияЧисленные (Матлаб)метод матрицы переноса (трансфер-матрицы)метод матрицы
- 74. 59 статей, 67 докладовPhys.Rev. A, EOptics ExpressOptics
- 75. ГрантыРФФИ:02-02-16325-а (2002 – 2004)03-02-06018-мас (2003), руководитель03-02-16052-а (2003
- 76. Премии2003 – лауреат премии губернатора Красноярского
- 77. Лекционные курсы (СибФУ)Механика 2004-2010Концепции современного естествознания 2003-2004Дискретная математика 2004-2005Молекулярная физика 2006-2009Optical Physics 2014-2016
- 78. Спасибо за внимание
- 79. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Семинар НОиММ КЭ МГУ, 03 июня 2016 года
Локализованные волны в
фотонном кристалле: частотная дисперсия, керровская нелинейность и оптическая анизотропия
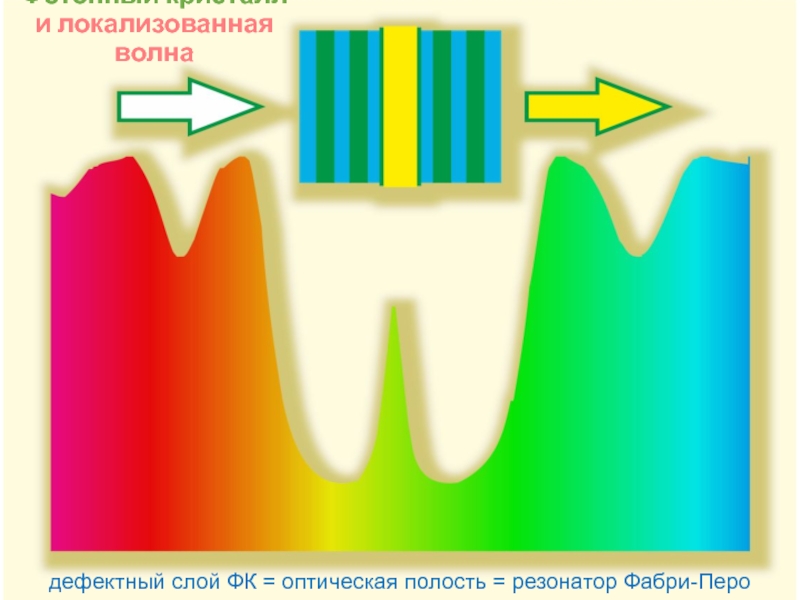
консультант: д. ф.-м. н., проф. Ветров С.Я.Слайд 6Фотонный кристалл
и локализованная волна
дефектный слой ФК = оптическая полость =
резонатор Фабри-Перо
Слайд 7Локализованные волны
O
Частотная дисперсия
Металл-диэлектрический нанокомпозит
Многоуровневая квантовая система
Керровская нелинейность
Оптическая необратимость
Оптическая анизотропия
Квазипересечение
оптических мод
Бистабильность жидкого кристалла
Геометрическая фаза и спектральные сдвиги
Хиральные поверхностные состояния
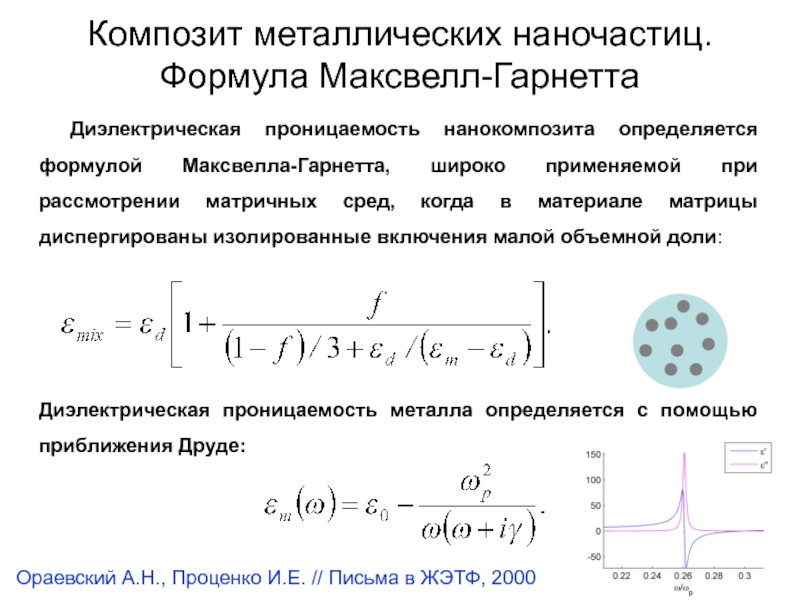
Слайд 9Диэлектрическая проницаемость нанокомпозита определяется формулой Максвелла-Гарнетта, широко применяемой при рассмотрении
матричных сред, когда в материале матрицы диспергированы изолированные включения малой
объемной доли:Диэлектрическая проницаемость металла определяется с помощью приближения Друде:
Композит металлических наночастиц.
Формула Максвелл-Гарнетта
Ораевский А.Н., Проценко И.Е. // Письма в ЖЭТФ, 2000
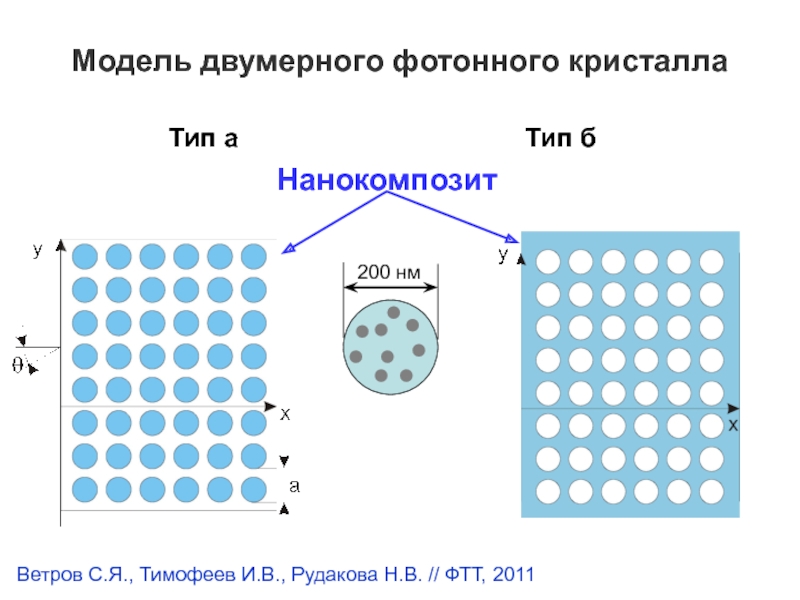
Слайд 10Модель двумерного фотонного кристалла
Тип б
Тип аНанокомпозит
Ветров С.Я., Тимофеев И.В., Рудакова Н.В. // ФТТ, 2011
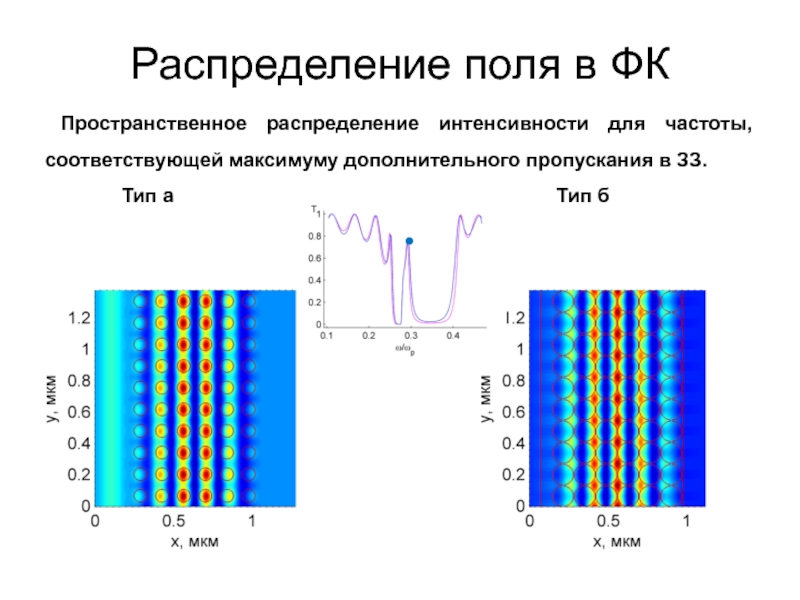
Слайд 11Пространственное распределение интенсивности для частоты, соответствующей максимуму дополнительного пропускания в
ЗЗ.
Тип а
Тип б Распределение поля в ФК
Слайд 12Модифицированный метод плоских волн
где
где
Беликов А.В., Богданова М.В., Лозовик Ю.Е. //
Мат Моделирование, 2007
Слайд 13
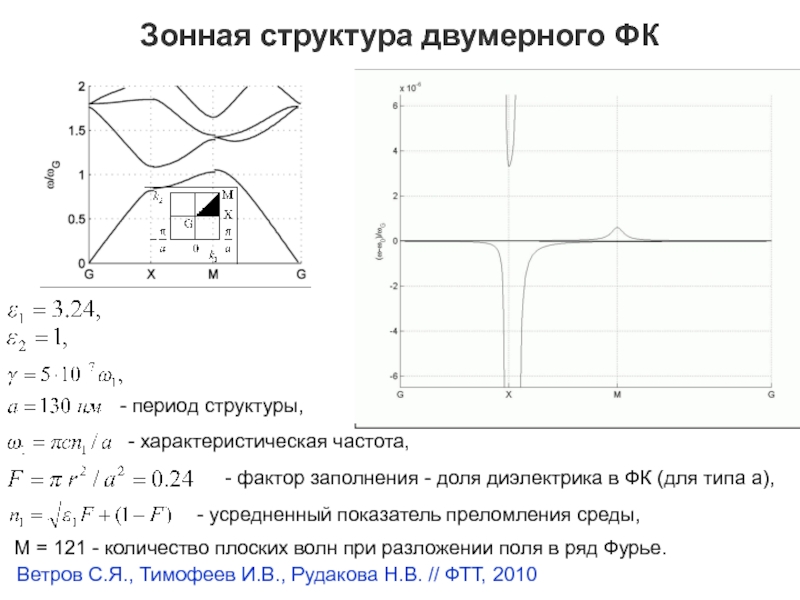
Зонная структура двумерного ФК
- усредненный показатель преломления среды,
M = 121
- количество плоских волн при разложении поля в ряд Фурье.
-
характеристическая частота,- фактор заполнения - доля диэлектрика в ФК (для типа а),
- период структуры,
Ветров С.Я., Тимофеев И.В., Рудакова Н.В. // ФТТ, 2010
Слайд 14
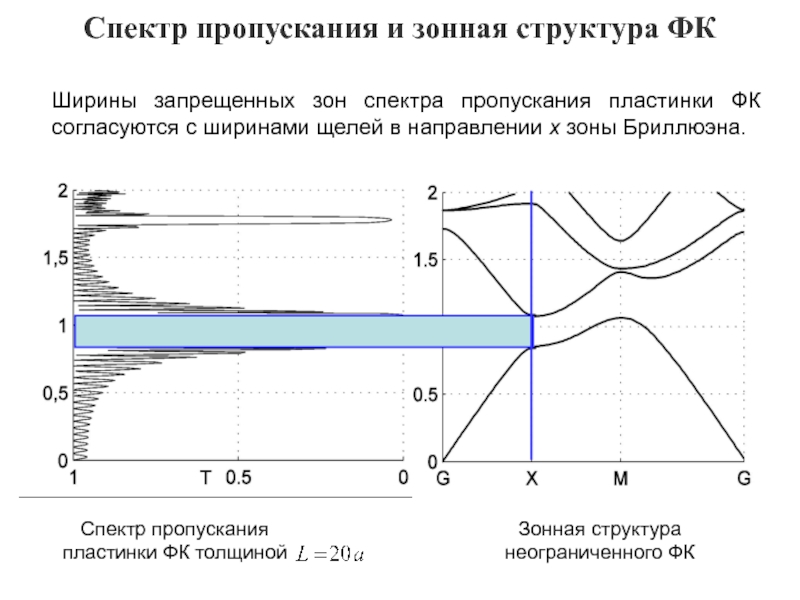
Спектр пропускания и зонная структура ФК
Ширины запрещенных зон спектра пропускания
пластинки ФК согласуются с ширинами щелей в направлении x зоны
Бриллюэна.Спектр пропускания пластинки ФК толщиной
Зонная структура неограниченного ФК
Слайд 15Оптическое таммовское состояние
Тамм ЖЭТФ 1933
Кавокин 2005
Калитеевский 2007
Виноградов УФН 2010
Афиногенов 2013
уравнение
Шредингера
уравнение Максвелла
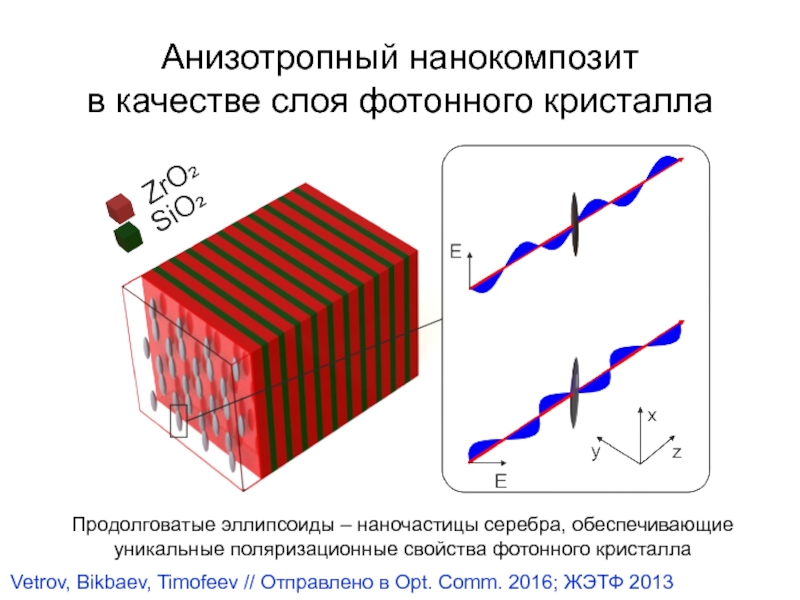
Слайд 16Анизотропный нанокомпозит
в качестве слоя фотонного кристалла
Продолговатые эллипсоиды – наночастицы серебра,
обеспечивающие уникальные поляризационные свойства фотонного кристалла
Vetrov, Bikbaev, Timofeev //
Отправлено в Opt. Comm. 2016; ЖЭТФ 2013Слайд 17db = 55 нм.
da = 110 нм
db = 40 нм.
da = 74 нм.
Спектр пропускания системы для
различных величин отношения длин полуосей наносфероида при фиксированном факторе заполнения
и толщине нанокомпозитного слоя. dmix=150 нм, f=0,3Слайд 19Рис.7. Коэффициент пропускания T ФК, сопряженного со слоем НК, в
зависимости от длины волны падающего света. Синим цветом показана действительная
часть ДП НК (а). Параметры Wd = 343.4 нм, Wa = 116 нм, Wb = 163.3 нм, We = 168 нм, β = (0.87)3, εm = 4, εc = 10, f = 0 (черный), f = 0.4 (пурпурный)Два ОТС в двух запрещенных зонах
Слайд 20Локализованные волны
Частотная дисперсия
Металл-диэлектрический нанокомпозит
Многоуровневая квантовая система
Керровская нелинейность
Оптическая необратимость
Оптическая анизотропия
Квазипересечение
оптических мод
Бистабильность жидкого кристалла
Геометрическая фаза и спектральные сдвиги
Хиральные поверхностные состояния
O
Слайд 21Электромагнитно индуцированная прозрачность и ультрамедленный свет
Harris, S.E. et al Nature,
1999
V.G. Arkhipkin, Yu.I.Heller, Phys.Lett., 1983
Слайд 22ЭИП в коротких импульсах
Свет двух резонансных частот в виде плоских
волн одинаковой линейной поляризации нормально падает на газообразную среду трехуровневых
атомов. Одномерная нестационарная задача.Схема атомных уровней: 1 основное состояние, 2 метастабильное.
Слайд 23ЭИП и замедление скорости импульса
а
б
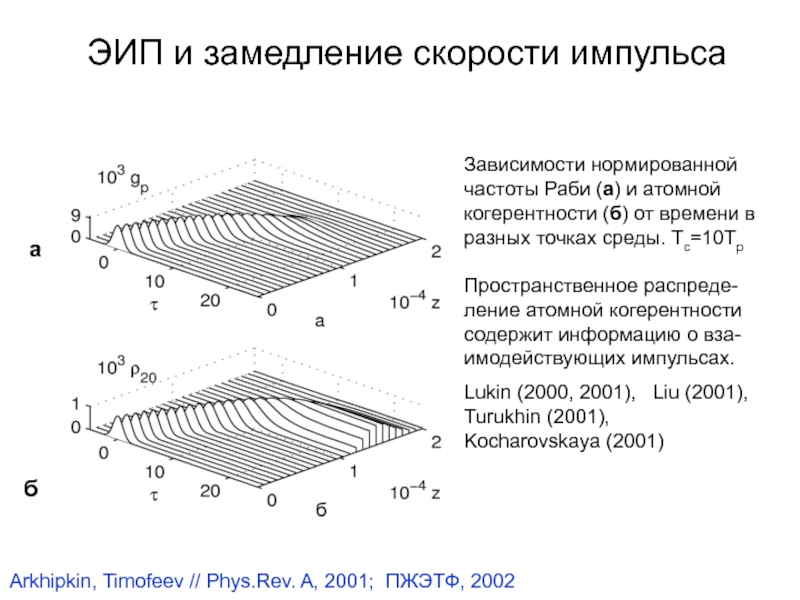
Зависимости нормированной частоты Раби (а) и
атомной когерентности (б) от времени в разных точках среды. Tc=10Tp
Пространственное
распреде-ление атомной когерентности содержит информацию о вза-имодействующих импульсах. Lukin (2000, 2001), Liu (2001), Turukhin (2001), Kocharovskaya (2001)
Arkhipkin, Timofeev // Phys.Rev. A, 2001; ПЖЭТФ, 2002
Слайд 24Временная эволюция нормированных частот Раби импульсов на различных глубинах среды
(а – на входе, в – на выходе).
Пробный импульс –
сплошная линия; управляющий – пунктир.Время измеряется в полуширинах пробного импульса.
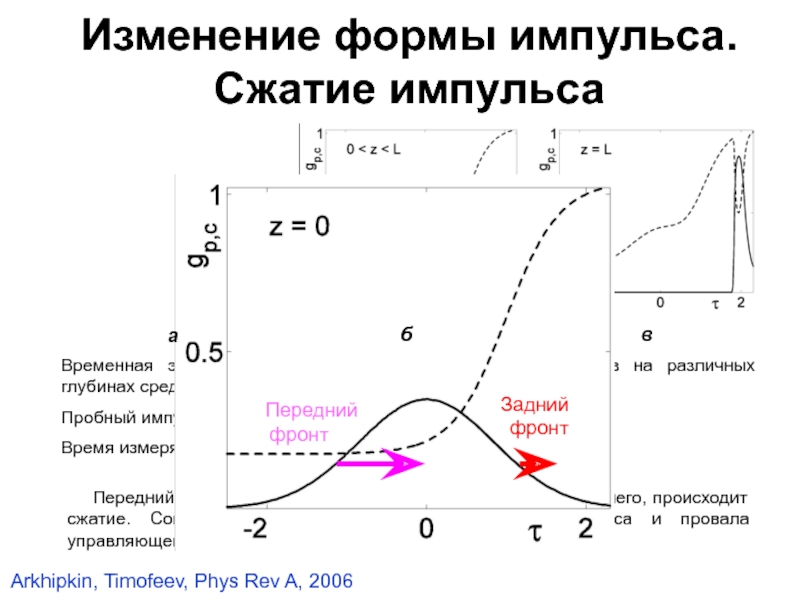
Передний край пробного импульса замедляется сильнее заднего, происходит сжатие. Согласованное распространение пробного импульса и провала управляющего поля напоминают адиабатонную пару.
a
б
в
Изменение формы импульса.
Сжатие импульса
Передний фронт
Задний фронт
Arkhipkin, Timofeev, Phys Rev A, 2006
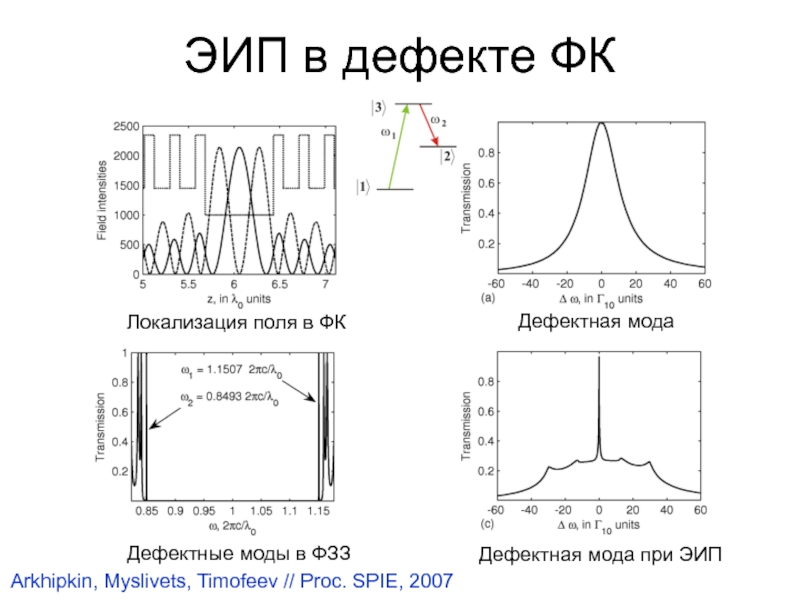
Слайд 25ЭИП в дефекте ФК
Локализация поля в ФК
Дефектные моды в ФЗЗ
Дефектная
мода при ЭИП
Дефектная мода
Arkhipkin, Myslivets, Timofeev // Proc. SPIE, 2007
Слайд 26Локализованные волны
Частотная дисперсия
Металл-диэлектрический нанокомпозит
Многоуровневая квантовая система
Керровская нелинейность
Оптическая необратимость
Оптическая анизотропия
Квазипересечение
оптических мод
Бистабильность жидкого кристалла
Геометрическая фаза и спектральные сдвиги
Хиральные поверхностные состояния
O
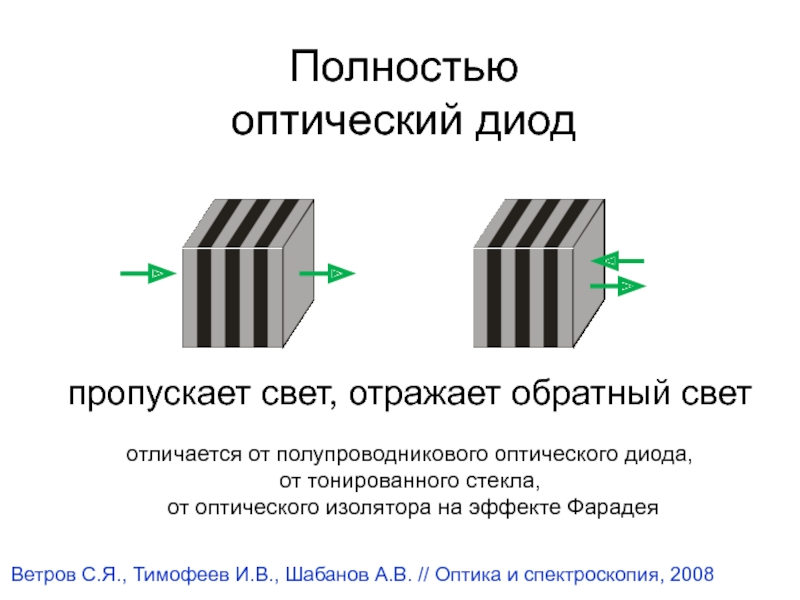
Слайд 27Полностью
оптический диод
пропускает свет, отражает обратный свет
отличается от полупроводникового оптического диода,
от
тонированного стекла,
от оптического изолятора на эффекте Фарадея
Ветров С.Я., Тимофеев
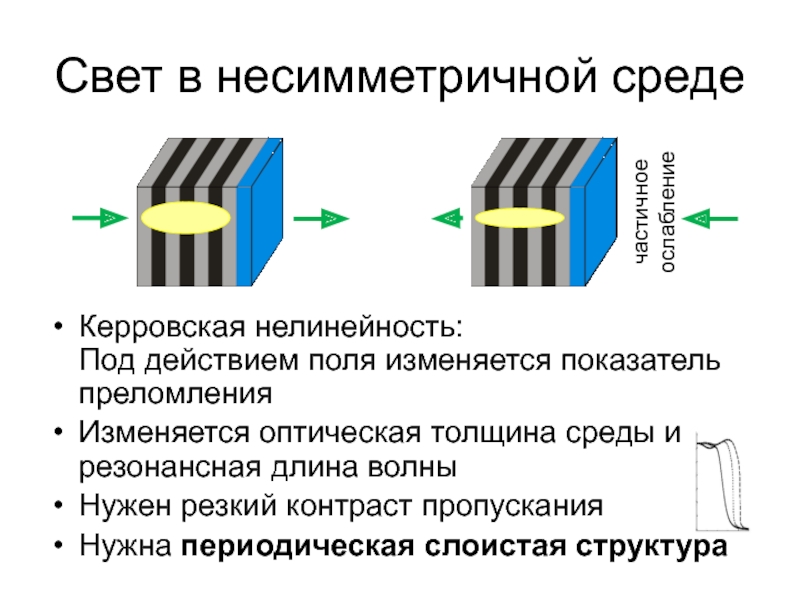
И.В., Шабанов А.В. // Оптика и спектроскопия, 2008 Слайд 28Свет в несимметричной среде
Керровская нелинейность:
Под действием поля изменяется показатель преломления
Изменяется
оптическая толщина среды и резонансная длина волны
Нужен резкий контраст пропускания
Нужна
периодическая слоистая структурачастичное ослабление
Слайд 32Какой длительности должен быть импульс, чтобы поле можно было считать
стационарным?
Длительность импульса ~10-13 c
Слайд 33Распределение электрического и магнитного поля в слоях
n – номер слоя.
TM
(transfer matrix) – метод трансфер матрицы
Слайд 35FDTD (the Finite-Difference Time-Domain Method) – метод конечных разностей во
временной области
Слайд 38Локализованные волны
Частотная дисперсия
Металл-диэлектрический нанокомпозит
Многоуровневая квантовая система
Керровская нелинейность
Оптическая необратимость
Оптическая анизотропия
Квазипересечение
оптических мод
Бистабильность жидкого кристалла
Геометрическая фаза и спектральные сдвиги
Хиральные поверхностные состояния
O
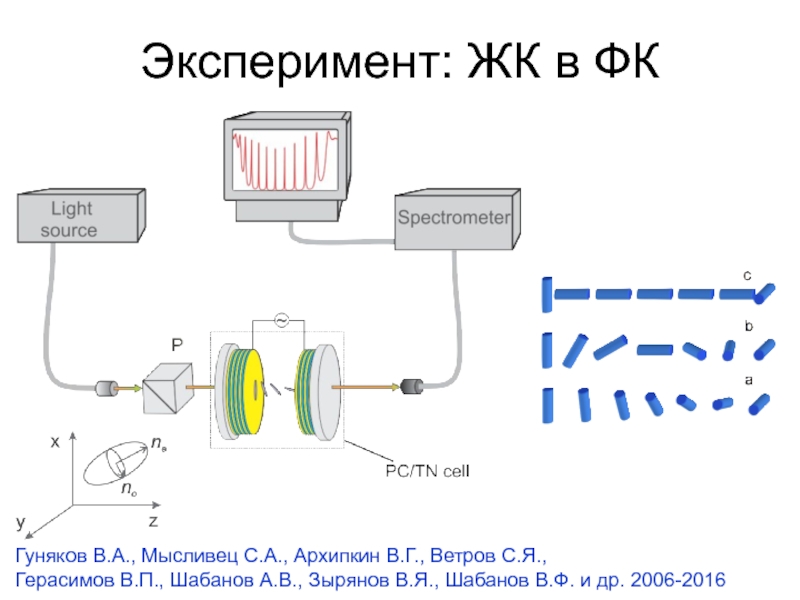
Слайд 40Эксперимент: ЖК в ФК
Гуняков В.А., Мысливец С.А., Архипкин В.Г., Ветров
С.Я.,
Герасимов В.П., Шабанов А.В., Зырянов В.Я., Шабанов В.Ф. и др.
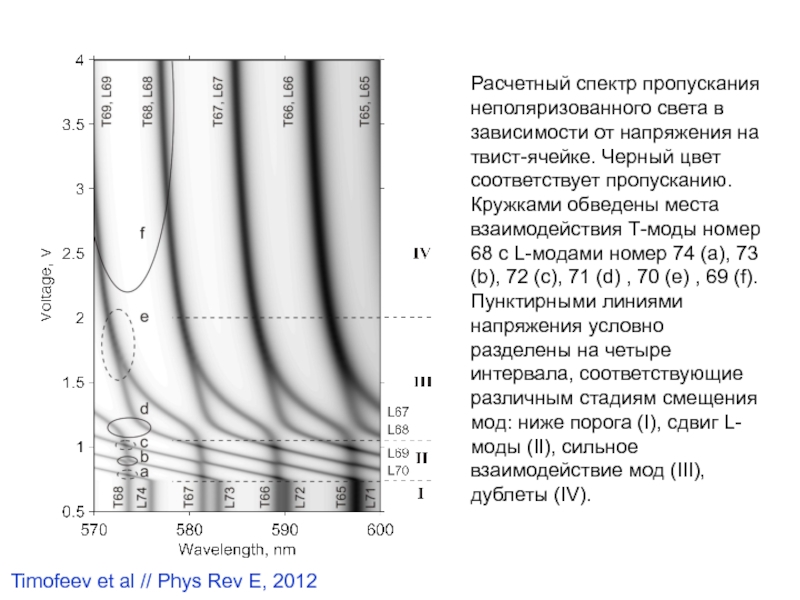
2006-2016Слайд 42Расчетный спектр пропускания неполяризованного света в зависимости от напряжения на
твист-ячейке. Черный цвет соответствует пропусканию. Кружками обведены места взаимодействия Т-моды
номер 68 с L-модами номер 74 (а), 73 (b), 72 (c), 71 (d) , 70 (e) , 69 (f). Пунктирными линиями напряжения условно разделены на четыре интервала, соответствующие различным стадиям смещения мод: ниже порога (I), сдвиг L-моды (II), сильное взаимодействие мод (III), дублеты (IV).Timofeev et al // Phys Rev E, 2012
Слайд 43Локализованные волны
Частотная дисперсия
Металл-диэлектрический нанокомпозит
Многоуровневая квантовая система
Керровская нелинейность
Оптическая необратимость
Оптическая анизотропия
Квазипересечение
оптических мод
Бистабильность жидкого кристалла
Геометрическая фаза и спектральные сдвиги
Хиральные поверхностные состояния
O
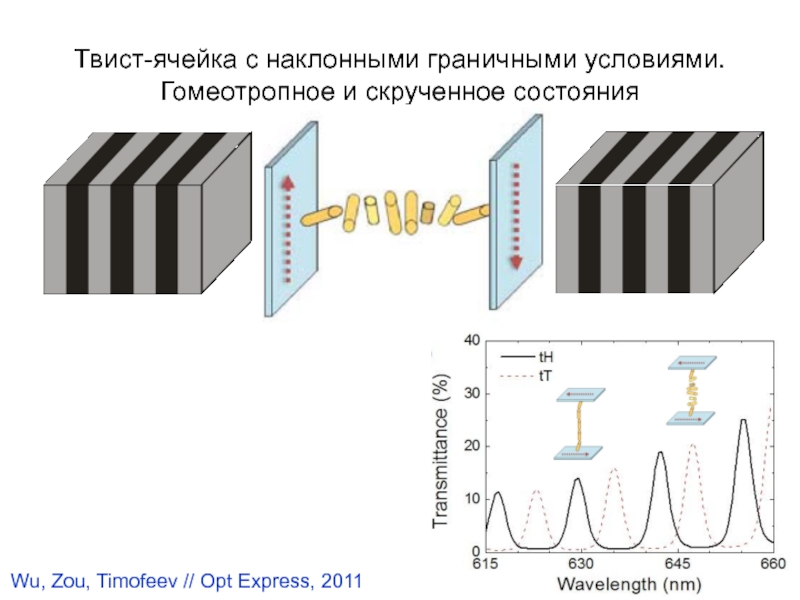
Слайд 44Твист-ячейка с наклонными граничными условиями.
Гомеотропное и скрученное состояния
Wu, Zou, Timofeev
// Opt Express, 2011
Слайд 46Метод расчета. Упругие силы
гуковский
наклон
гуковское
скручивание
наклон
Ферма
аналогия:
луч в соленой воде
катеноид мыльной пленки
Слайд 48Расчет поля в анизотропной структуре.
Матричная форма уравнений Максвелла
Berreman D.W. //
JOSA 1972
Слайд 50Локализованные волны
Частотная дисперсия
Металл-диэлектрический нанокомпозит
Многоуровневая квантовая система
Керровская нелинейность
Оптическая необратимость
Оптическая анизотропия
Квазипересечение
оптических мод
Бистабильность жидкого кристалла
Геометрическая фаза и спектральные сдвиги
Хиральные поверхностные состояния
O
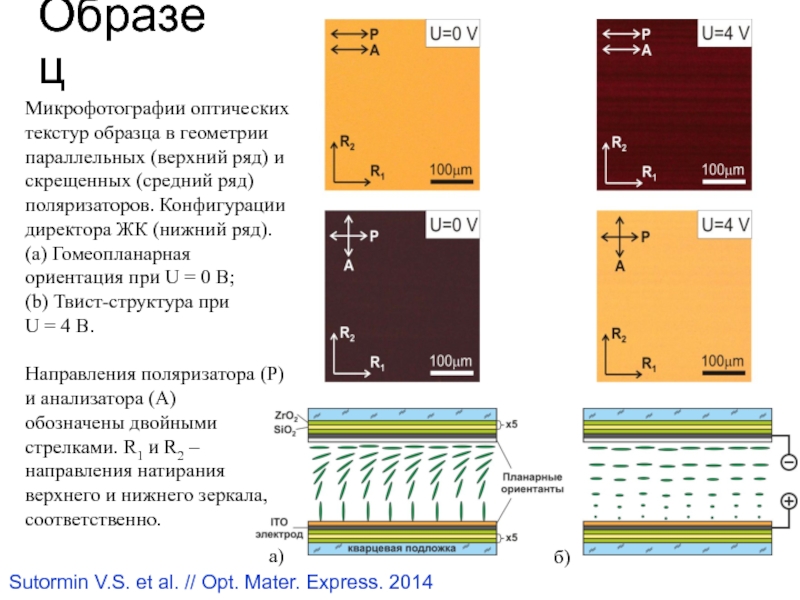
Слайд 52Микрофотографии оптических текстур образца в геометрии параллельных (верхний ряд) и
скрещенных (средний ряд) поляризаторов. Конфигурации директора ЖК (нижний ряд). (а)
Гомеопланарная ориентация при U = 0 В; (b) Твист-структура при U = 4 В.Направления поляризатора (Р) и анализатора (А) обозначены двойными стрелками. R1 и R2 – направления натирания верхнего и нижнего зеркала, соответственно.
б)
а)
Образец
Sutormin V.S. et al. // Opt. Mater. Express. 2014
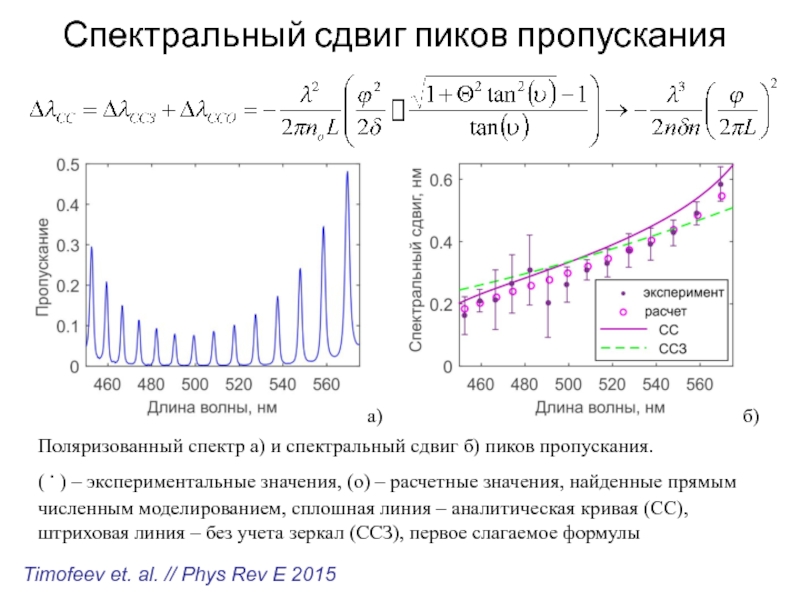
Слайд 53Спектральный сдвиг пиков пропускания
Поляризованный спектр а) и спектральный сдвиг б)
пиков пропускания. () – экспериментальные значения, (o) – расчетные значения, найденные
прямым численным моделированием, сплошная линия – аналитическая кривая (СС), штриховая линия – без учета зеркал (ССЗ), первое слагаемое формулыб)
а)
Timofeev et. al. // Phys Rev E 2015
Слайд 59Локализованные волны
Частотная дисперсия
Металл-диэлектрический нанокомпозит
Многоуровневая квантовая система
Керровская нелинейность
Оптическая необратимость
Оптическая анизотропия
Квазипересечение
оптических мод
Бистабильность жидкого кристалла
Геометрическая фаза и спектральные сдвиги
Хиральные поверхностные состояния
O
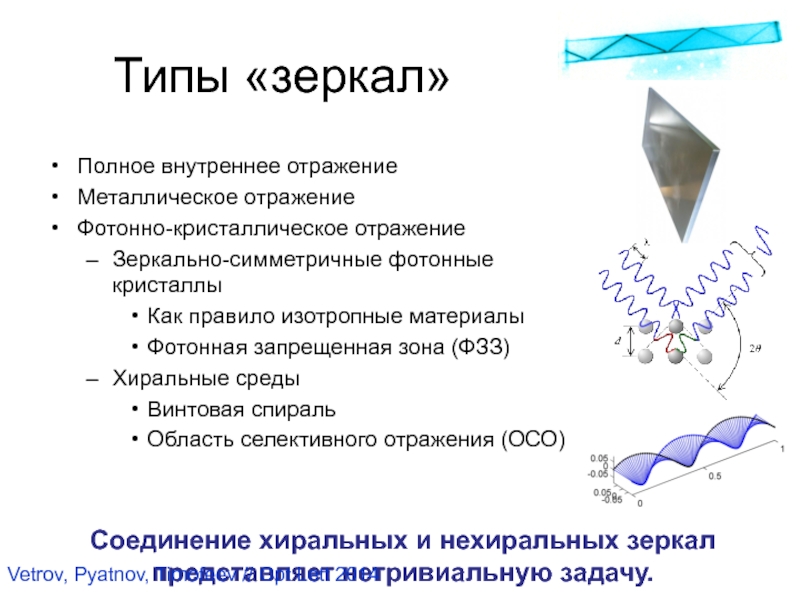
Слайд 60Типы «зеркал»
Полное внутреннее отражение
Металлическое отражение
Фотонно-кристаллическое отражение
Зеркально-симметричные фотонные кристаллы
Как правило изотропные
материалы
Фотонная запрещенная зона (ФЗЗ)
Хиральные среды
Винтовая спираль
Область селективного отражения (ОСО)
Соединение хиральных
и нехиральных зеркал представляет нетривиальную задачу.Vetrov, Pyatnov, Timofeev // Opt Lett 2014
Слайд 61Отражение от ХЖК
Поляризация отражённого света
Отражение от диэлектрика или зеркала
Правая
Левая
Правая
Правая
Слайд 63Сохраняющее поляризацию анизотропное зеркало
на основе металл-диэлектрического нанокомпозита
Рудакова Н.В. и др.
подготовлено в Известия РАН 2016
Слайд 65Положительная обратная связь и геометрическая фаза
Тимофеев, Ветров // подготовлено в
Письма ЖЭТФ 2016
Слайд 69Коллеги
Архипкин
Василий
Григорьевич
Ветров
Степан
Яковлевич
Зырянов
Виктор
Яковлевич
Вей Ли,
Тайвань,
Тайнань
Слайд 70Коллеги
Гуняков
Владимир
Алексеевич
Сутормин
Виталий
Сергеевич
Вьюнышев
Андрей
Михайлович
Рудакова
Наталья
Викторовна
Слайд 71Коллеги
Бикбаев
Рашид
Гельмединович
Авдеева
Анастасия
Юрьевна
Панкин
Павел
Сергеевич
Пятнов
Максим
Владимирович
Слайд 72Творческие планы
Экспериментальная проверка спектральных сдвигов в холестерике и закрученном нематике,
обусловленных геометрической фазой
Металл-диэлектрический нанокомпозит:
неважно проводит свет, но хорошо отражает
Теория связанных
мод, поиск нуля пропускания в одномерных анизотропных структурахХиральные поверхностные оптические состояния, гибридные состояния
Слайд 73Методы исследования
Численные (Матлаб)
метод матрицы переноса (трансфер-матрицы)
метод матрицы рассеяния
метод Берремана (обобщение
на анизотропию)
метод Пендри (обобщение на двумерие)
метод конечных разностей во временной
области (FDTD)метод конечных элементов (FEM)
разложение по собственным функциям, плоским волнам
Аналитические, качественные
теория связанных мод, дисперсионные уравнения
метод характеристик
группы симметрий, кватернионы
сфера Пуанкаре, расслоение Хопфа
комплексная плоскость, стереографическая проекция
Слайд 7459 статей, 67 докладов
Phys.Rev. A, E
Optics Express
Optics Materials Express
Journal of
Optics
Optics Letters…
ЖЭТФ, Письма в ЖЭТФ
Физика твердого тела
Доклады Академии наук
Квантовая электроника
Оптика
и спектроскопия…Слайд 75Гранты
РФФИ:
02-02-16325-а (2002 – 2004)
03-02-06018-мас (2003), руководитель
03-02-16052-а (2003 – 2004),
14-02-31248-мол_а (2014-2015),
руководитель
Грант Президента Российской федерации (ФЦНТП):
МК-1292.2008.2, руководитель
НШ-6612.2006.3 (участник), НШ-3818.2008.3 (участник)
Президиум РАН,
СО РАН, РНП, ФЦП…МинОбр: 3.1276.2014.K
Заявка на Мегагрант 2017-2019
Слайд 76 Премии
2003 – лауреат премии губернатора Красноярского края молодым талантам.
2005
– лауреат премии главы города Красноярска молодым талантам.
2007 – почетный
диплом №94 «Достояние Сибири» в номинации «Наука и образование» за вклад в развитие сибирской науки. Награждали: Межрегиональная ассоциация «Сибирское соглашение», Сибирское межрегиональное отделение Национального фонда «Общественное признание».2008 – почетная грамота Сибирского отделения Российской академии наук (в г. Новосибирске).
2016 – благодарственное письмо губернатора Красноярского края.