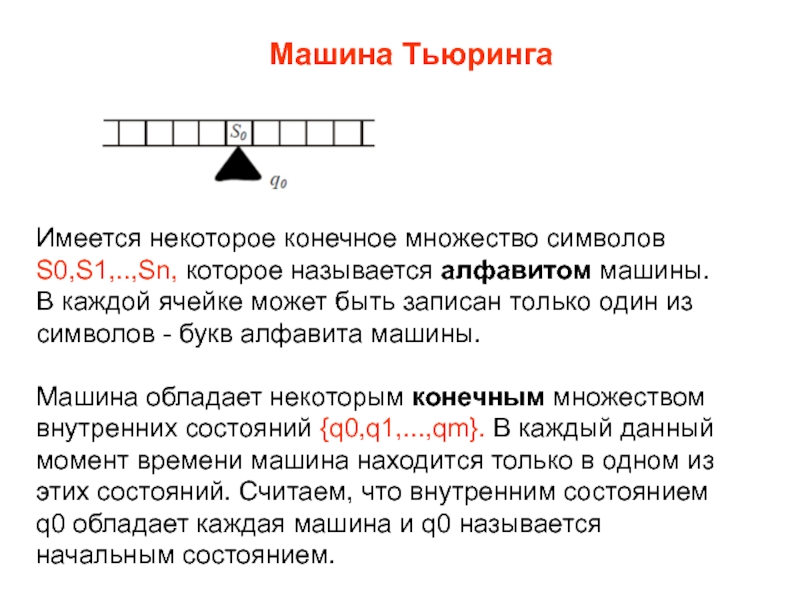
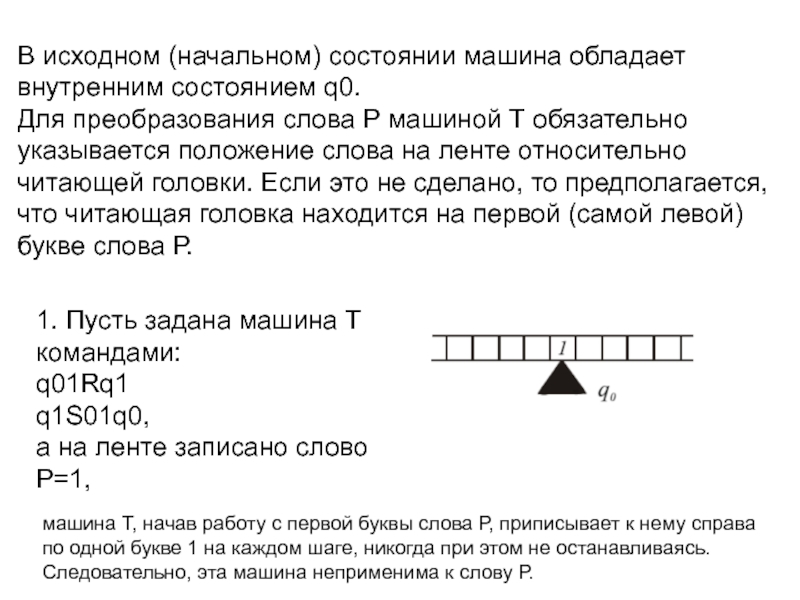
алфавитом машины. В каждой ячейке может быть записан только один
из символов - букв алфавита машины.Машина обладает некоторым конечным множеством внутренних состояний {q0,q1,...,qm}. В каждый данный момент времени машина находится только в одном из этих состояний. Считаем, что внутренним состоянием q0 обладает каждая машина и q0 называется начальным состоянием.