Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая логика
Содержание
- 1. Математическая логика
- 2. Понятие конечного автомата-преобразователя КА Мили называется шестерка объектов:
- 3. Понятие конечного автомата-преобразователя КА Мура называется шестерка объектов:
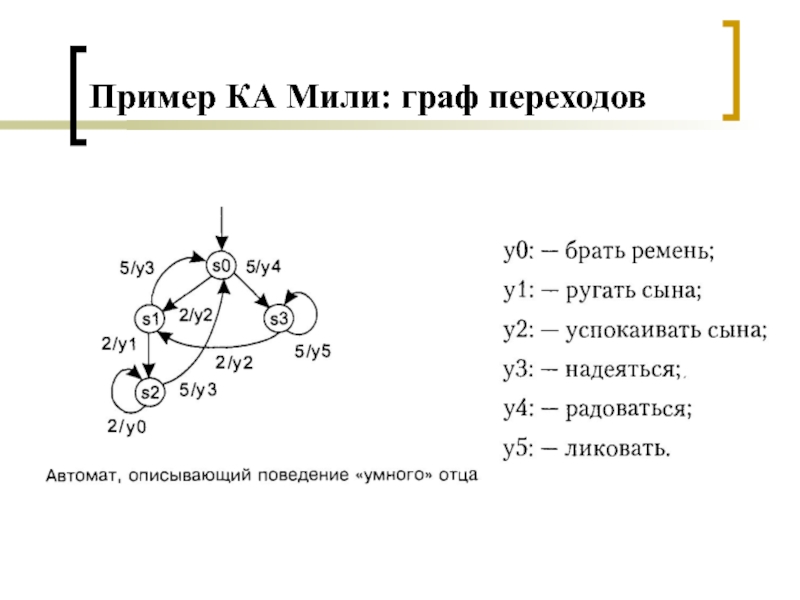
- 4. Пример КА Мили: граф переходов
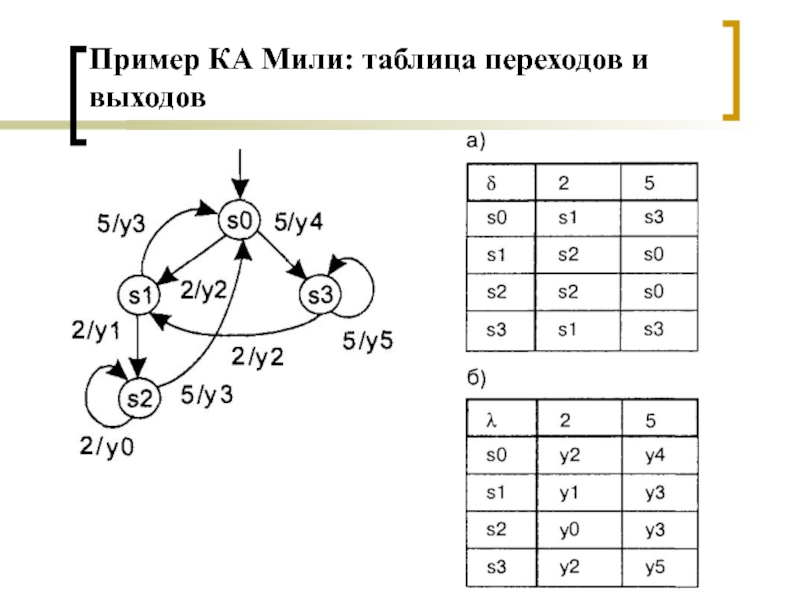
- 5. Пример КА Мили: таблица переходов и выходов
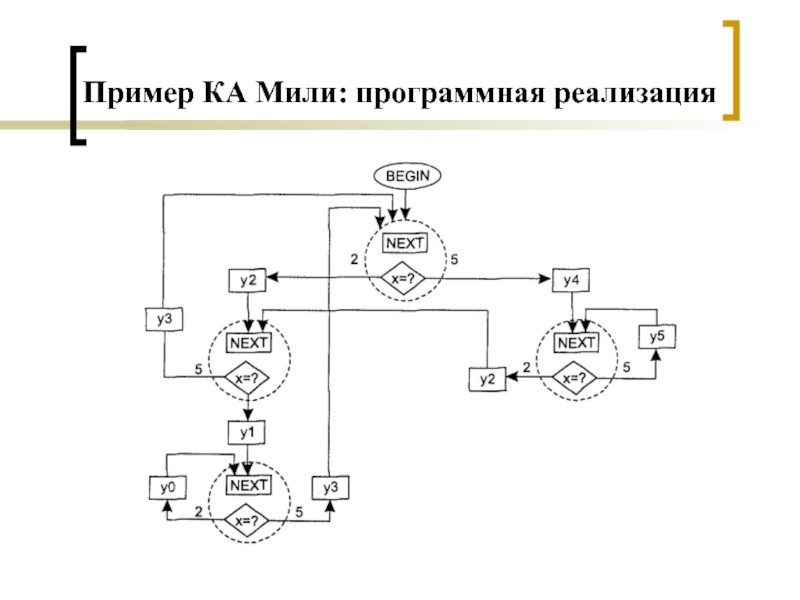
- 6. Пример КА Мили: программная реализация
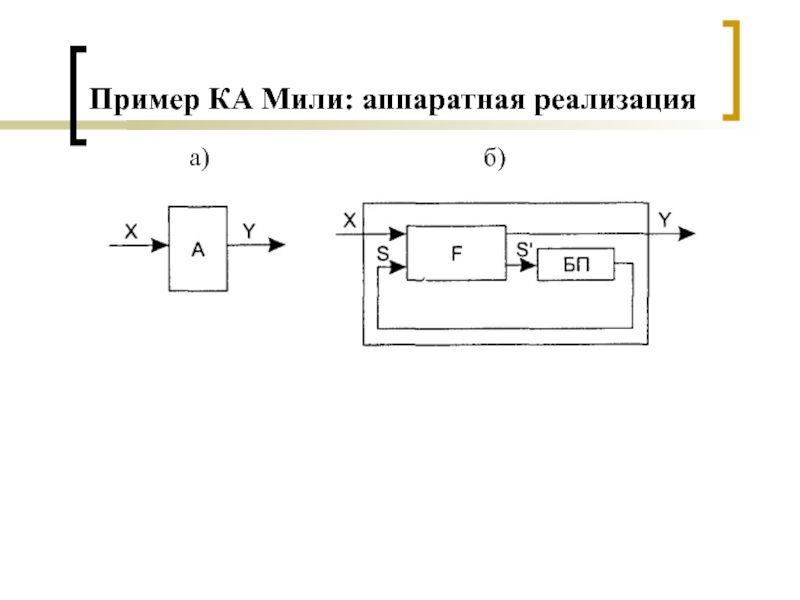
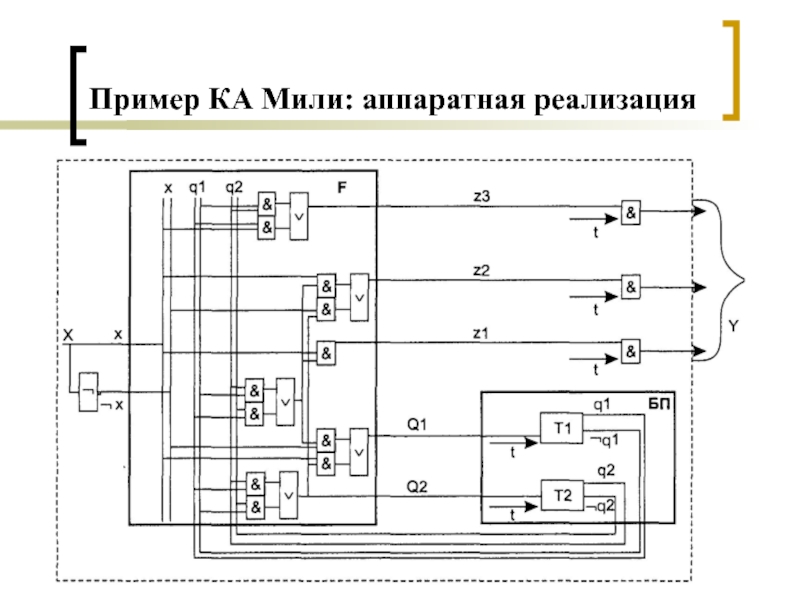
- 7. Пример КА Мили: аппаратная реализация
- 8. Пример КА Мили: аппаратная реализацияКодирование входных/выходных сигналов и состояний КА
- 9. Пример КА Мили: аппаратная реализация
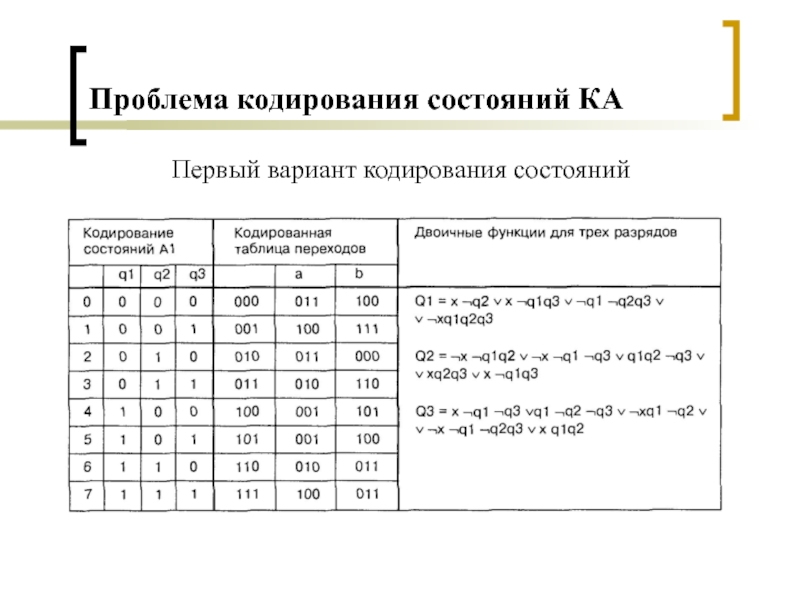
- 10. Проблема кодирования состояний КАПример таблицы переходов КА
- 11. Проблема кодирования состояний КАПервый вариант кодирования состояний
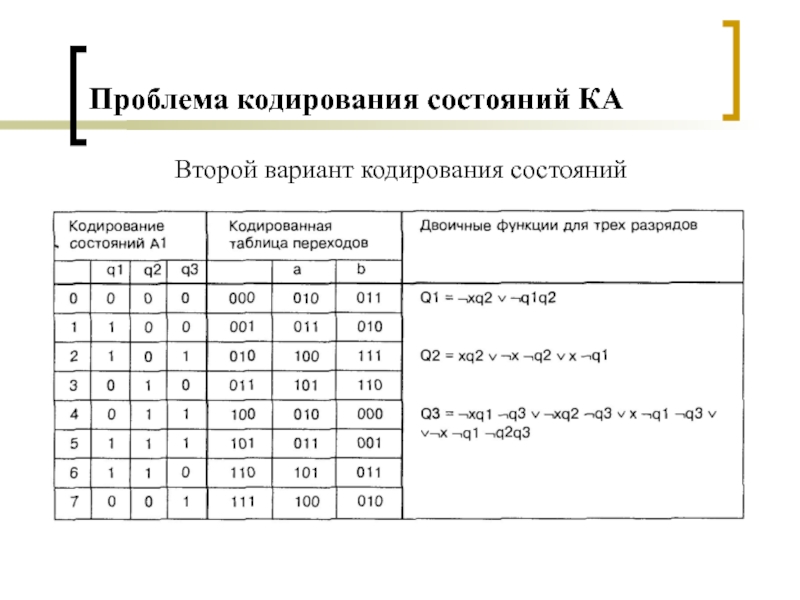
- 12. Проблема кодирования состояний КАВторой вариант кодирования состояний
- 13. Проблема кодирования состояний КАТретий вариант кодирования состояний
- 14. Конечные автоматы-распознаватели Зафиксируем некоторое конечное множество V и
- 15. Конечные автоматы-распознаватели КА-распознавателем называется пятерка объектов А =
- 16. Область применения КА Хотя теория конечных автоматов изучает
- 17. Область применения КА Из выступлений на семинаре «Software
- 18. Скачать презентанцию
Понятие конечного автомата-преобразователя КА Мили называется шестерка объектов: А = , где S – конечное непустое множество состояний; X – конечное непустое множество входных сигналов (входной алфавит); Y – конечное непустое множество выходных
Слайды и текст этой презентации
Слайд 2Понятие конечного автомата-преобразователя
КА Мили называется шестерка объектов:
А
= ,
где
S – конечное непустое
множество состояний;X – конечное непустое множество входных сигналов (входной алфавит);
Y – конечное непустое множество выходных сигналов (выходной алфавит);
s0 S – начальное состояние;
δ: SX S – функция переходов;
λ: SX Y – функция выходов.
Слайд 3Понятие конечного автомата-преобразователя
КА Мура называется шестерка объектов:
А
= ,
где
S – конечное непустое
множество состояний;X – конечное непустое множество входных сигналов (входной алфавит);
Y – конечное непустое множество выходных сигналов (выходной алфавит);
s0 S – начальное состояние;
δ: SX S – функция переходов;
λ: S Y – функция выходов.
Слайд 14Конечные автоматы-распознаватели
Зафиксируем некоторое конечное множество V и назовем его алфавитом.
- Элементы алфавита V, как обычно, будем называть буквами.
-
Конечные последовательности (цепочки) букв (в том числе и пустая последовательность), называются словами в алфавите V (ясно, что пустое слово не содержит букв; будем обозначать его буквой ). - Множество всех слов в алфавите V обозначается через V*.
Например, если V = {а, b, с}, то
V* = {, а, b, с, аа, ab, ac, ba, bb, bc, ca, cb, cc, aaa, aab, aac, aba, abb, ... }.
Очевидно, что хотя V конечно, V* – бесконечное счетное множество.
Любое множество слов в алфавите V называется языком над V. Язык над алфавитом V будем обозначать LV, ила просто L, если алфавит V фиксирован. Ясно, что множество L является языком над V тогда и только тогда, когда L есть подмножество множества V* , т.е. L V*.
Слайд 15Конечные автоматы-распознаватели
КА-распознавателем называется пятерка объектов
А = (S, X, s0,
δ, F),
где
S – конечное непустое множество состояний;
X V*
– конечное непустое множество входных сигналов (входной алфавит);s0 S – начальное состояние;
δ: S X → S – функция переходов;
F S – множество заключительных (финальных) состояний.
Слайд 16Область применения КА
Хотя теория конечных автоматов изучает очень простые модели,
она является фундаментом большого числа разнообразных приложений. Эти приложения –
от языковых процессоров до систем управления реального времени и протоколов связи – покрывают значительную долю систем, разработкой, реализацией и анализом которых занимается информатика.Слайд 17Область применения КА
Из выступлений на семинаре «Software 2000: a View
of the Future» 10 апреля 1994 года.
Brian Randell: «Я помню
Дуга Росса из компании SofTech, много лет назад говорившего, что 80 или даже 90 % информатики (Computer Science) будет в будущем основываться на теории конечных автоматов». Herve Gallaire: «Я знаю людей из «Боинга», занимающихся системами стабилизации самолетов с использованием чистой теории автоматов. Даже трудно себе представить, что им удалось сделать с помощью этой теории».
Brian Randell: «Большая часть теории автоматов была успешно использована в системных программах и текстовых фильтрах в OS UNIX. Это позволяет множеству людей работать на высоком уровне и разрабатывать очень эффективные программы».