Слайд 1Математическая статистика
Лекции по математике
Слайд 2И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Рекомендуемая литература
Кремер
Н.Ш. Теория вероятностей и математическая статистика. - М.: Банки и
биржи, ЮНИТИ, 2001 .
Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: В.Ш., 2002 .
Кропачева Н.Ю., Петросян Г.А. Элементы математической статистики. Учебное пособие по изучению курса высшей математики. – СПб.: Изд-во СПбГАСЭ, 2004. – 79 с.
Тимошина И.Р. Электронный конспект лекций по математической статистике. ВФ СПбГУСЭ, 2007.
Слайд 3И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Содержание
Основные законы
распределения статистических оценок
Точечная и интервальная оценки.
Метод моментов
Точность и надёжность
оценки
Построение доверительного интервала для оценки математического ожидания нормального распределения
Слайд 4И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Основные законы
распределения статистических оценок
Статистическая оценка параметра распределения это функция от
наблюдаемых случайных величин.
Статистическая оценка это тоже случайная величина!
Необходимо знать закон распределения статистической оценки.
Слайд 5И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Основные законы
распределения статистических оценок
Нормальный закон распределения
Распределение хи-квадрат
Распределение Стьюдента
Распределение Фишера-Снедекора.
Слайд 6И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
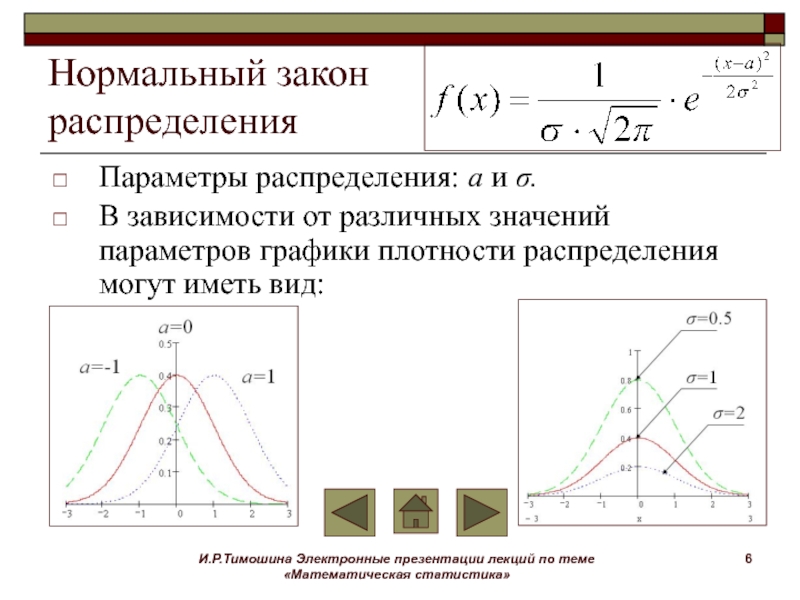
Нормальный закон
распределения
Параметры распределения: a и σ.
В зависимости от различных значений параметров
графики плотности распределения могут иметь вид:
Слайд 7И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Распределение
«хи-квадрат»
Если
случайные величины X1, X2,…, Xn - независимы, распределены по нормальному
закону, имеют нулевое математическое ожидание a=0 и σ =1,
то величина
распределена по закону «хи-квадрат» с n степенями свободы. Число является n параметром распределения.
Слайд 8И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Распределение «хи-квадрат»
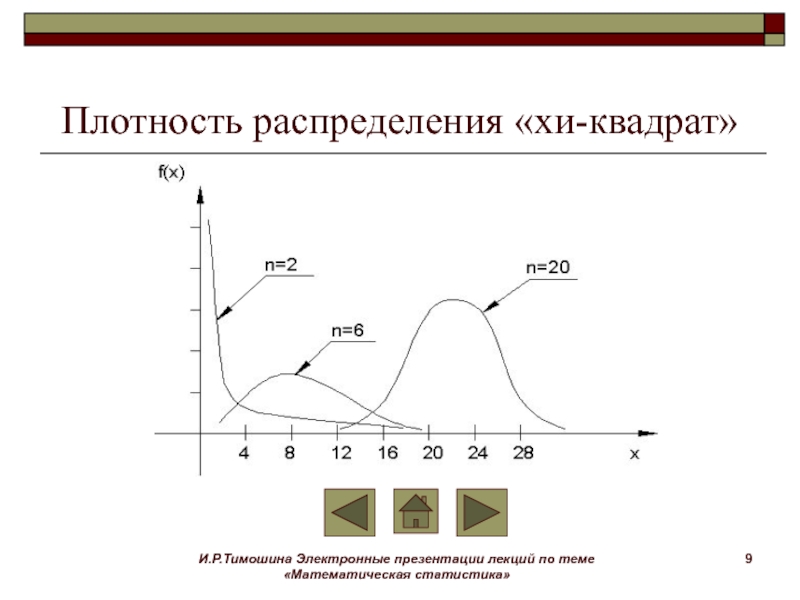
При
больших значениях п распределение случайной величины
близко к нормальному распределению с параметрами a=n, σ2=2n. Однако при малых значениях п функция плотности случайной величины значительно отличается от кривой нормального распределения.
Слайд 9И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Плотность распределения
«хи-квадрат»
Слайд 10И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Распределение
Стьюдента
Пусть
случайные величины Z, X1, X2,…, Xn - независимы, распределены по
нормальному закону, имеют нулевое математическое ожидание a=0 и σ=1. Тогда величина
распределена по закону
Стьюдента n с степенями
свободы.
Слайд 11И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Распределение Стьюдента
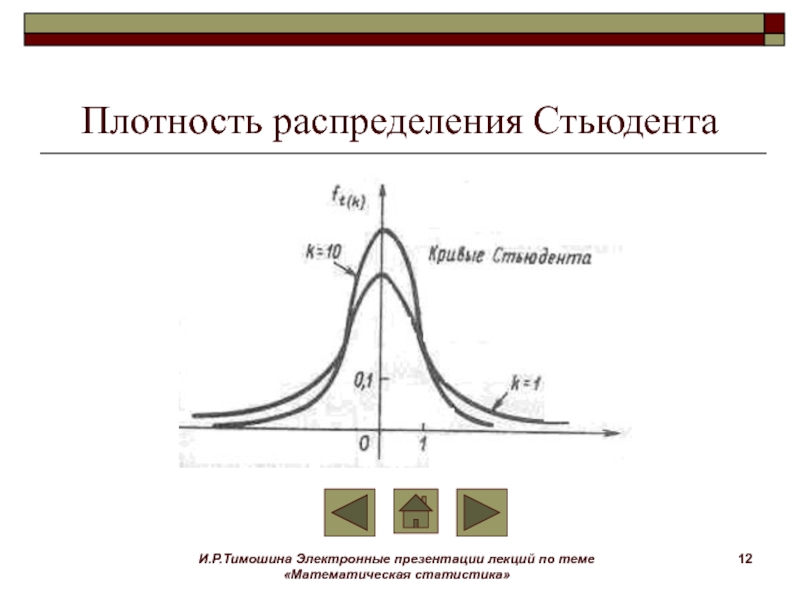
Это
распределение впервые в 1908 году было использовано английским математиком В.Госсетом,
который подписывал свои работы псевдонимом Стьюдент (Студент).
Распределение Стьюдента симметрично относительно нуля и значения функции плотности распределения табулированы. При больших значениях k кривая плотности близка к кривой нормального распределения.
Слайд 12И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Плотность распределения
Стьюдента
Слайд 13И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Распределение
Фишера-Снедекора
Пусть
и случайные величины, имеющие
распределение «хи-квадрат» с n и m степенями свободы соответственно. Тогда величина имеет
распределение Фишера-Снедекора.
Слайд 14И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Точечная и
интервальная оценки. Доверительный интервал
Напомним, что статистической оценкой неизвестного параметра распределения
называется функция от наблюдаемых случайных величин, которая позволяет вычислить приближённое значение этого параметра.
Слайд 15И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Точечная оценка
Точечной
называют оценку, которая определяется одним числом. Рассмотренные ранее оценки (
и ) являются точечными.
При выборке малого размера точечная оценка может существенно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам.
Слайд 16И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Интервальная оценка
Интервальной
называют оценку, которая определяется двумя числами – концами интервала. Интервальные
оценки позволяют установить точность и надёжность оценки.
Рассмотрим методы вычисления оценок распределения.
Слайд 17И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Метод моментов
для точечной оценки параметров распределения
Пусть известен вид функции плотности распределения
вероятностей случайной величины. Предположим, что эта функция зависит от одного параметра, к примеру, если распределение показательное, то функция распределения .
Слайд 18И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Метод моментов
для точечной оценки параметров распределения
Пусть требуется оценить неизвестный параметр λ,
используя полученные выборочные статистические данные.
Для нахождения неизвестного параметра распределения нужно составить уравнение.
Слайд 19И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Метод моментов
для точечной оценки параметров распределения
К примеру, из определения математического ожидания
величины, распределённой по показательному закону, следует
Следовательно, .
Заменяя математическое ожидание его оценкой, т.е. выборочной средней, получим оценку неизвестного параметра .
Слайд 20И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Метод моментов
для точечной оценки параметров распределения
Если плотность распределения зависит от двух
параметров, то для их определения нужно использовать уже два уравнения. В качестве таких уравнений используют формулы, задающие математическое ожидание и дисперсию. Для получения оценок более двух параметров используют уравнения, задающие начальные или центральные моменты.
Слайд 21И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Пример. Случайная
величина распределена по
показательному закону. Интервальный вариационный
ряд имеет вид:
Оценить
параметр λ показательного распределения.
Решение. Вычислим выборочную среднюю:
Так как в показательном распределении ,
то оценка .
Слайд 22И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Точность оценки.
Пусть найденная по данным выборки величина θ* служит оценкой неизвестного
параметра θ. Оценка определяет θ* тем точнее, чем меньше величина|θ - θ*| , т.е. чем меньше δ в неравенстве |θ - θ*|< δ, δ>0. Положительное число δ характеризует точность оценки.
Слайд 23И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Точность и
надёжность оценки.
Так как θ* случайная величина, то и |θ
- θ*| - случайная величина. Поэтому можно говорить лишь о вероятности γ, с которой выполняется неравенство P(|θ - θ*|< δ).
Надёжностью оценки (доверительной вероятностью) называется вероятность γ, с которой выполняется неравенство
γ=P(|θ - θ*|)< δ).
Слайд 24И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Точность и
надёжность оценки. Доверительный интервал
Пусть Р(|θ - θ*|< δ)= γ. Заменив
неравенство |θ - θ*|< δ на равносильное ему двойное неравенство θ* - δ < θ < θ*+ δ, имеем
Р(θ* - δ < θ < θ*+ δ)=γ.
Это соотношение следует понимать так: вероятность того, что интервал заключает в себе оцениваемый параметр , равна γ.
Слайд 25И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Доверительный интервал
Доверительным
называют интервал
(θ* - δ ; θ*+ δ), который покрывает
параметр θ, а параметр γ называют доверительной вероятностью или уровнем доверия.
Слайд 26И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Задачи на
построение доверительного интервала
Задача 1. Пусть X случайная величина, распределённая нормально,
причём среднее квадратическое отклонение σx известно. Построить доверительный интервал, покрывающий неизвестный параметр а (математическое ожидание Мx) с надёжностью γ, с учётом полученного значения выборочного среднего .
Слайд 27И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Построение доверительного
интервала
Как уже отмечалось, выборочная средняя является случайной величиной
.
Величина имеет нормальный закон распределения, так как является суммой независимых нормально распределённых величин. Как уже было показано ранее,
; .
Слайд 28И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Построение доверительного
интервала
Потребуем, чтобы выполнялось соотношение
Воспользуемся формулой
, которая была выведена для нормально распределённых случайных величин. В этой формуле функция Ф(t) - табулированная функция Лапласа.
Слайд 29И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Построение доверительного
интервала
Применяя эту формулу к случайной величине
и учитывая, что ;
, получим: ,
где .
Слайд 30И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Построение доверительного
интервала
Из полученной формулы, задавая точность оценки δ, можно вычислить её
надёжность γ=2Ф(t), а желая достичь заданной надёжности оценки γ, можно оценить величину точности δ.
Слайд 31И.Р.Тимошина Электронные презентации лекций по теме
«Математическая статистика»
Пример. Случайная
величина X имеет нормальное
распределение с известным средним квадратическим
отклонением
σ=3. Найти доверительные интервалы для
оценки неизвестного математического ожидания Mx
по выборочному среднему , если объём выборки
n=36 и задана надёжность оценки γ=0,95.
Решение. Найдём t из соотношения 2Ф(t)=0,95,
Ф(t)=0,475. По таблицам для функции Лапласа находим
t=1,96. Найдём точность оценки:
Ответ. Доверительный интервал
С вероятностью 0.95 математическое ожидание
принадлежит этому интервалу.