Математическая статистика

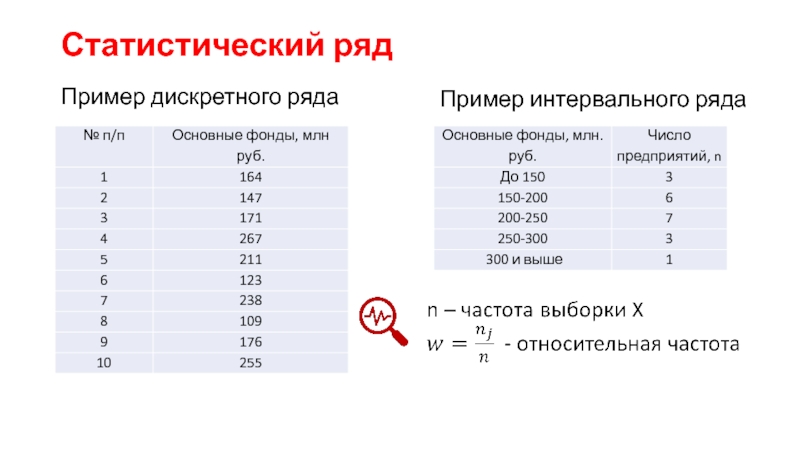
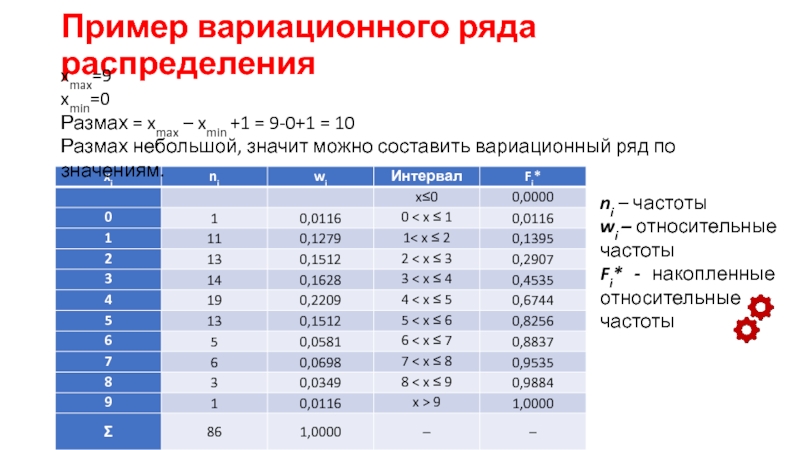
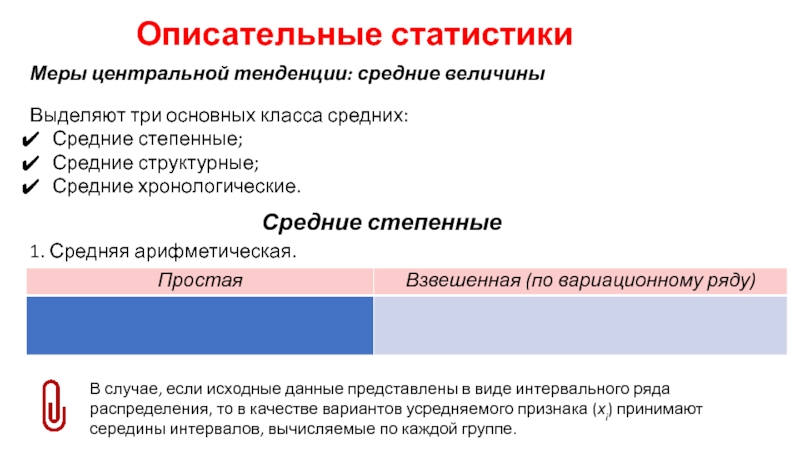
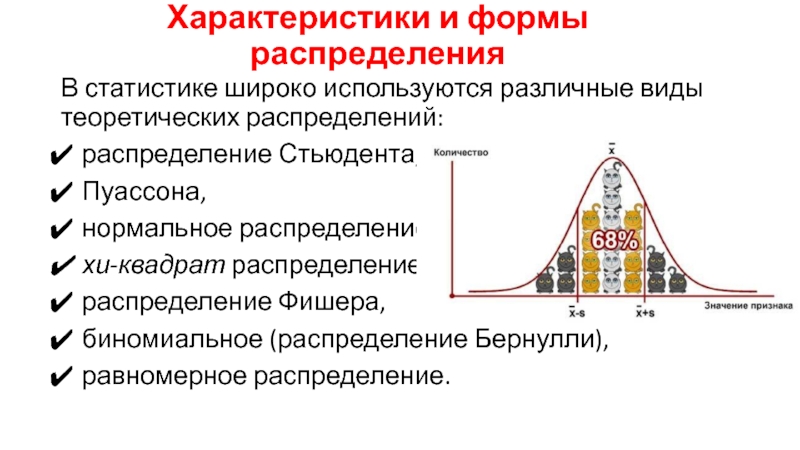
роль в механизме управления экономикой выполняет статистика. Она осуществляет сбор,

научную обработку, обобщение и анализ информации, характеризующей социально-экономическое развитие страны.
Термин «статистика» происходит от латинских «Status», что означает «определенное состояние явления, положение вещей», и «Stato» – «государство». Он был введен в научный оборот в 1749 году немецким ученым Готфридом Ахенвалем, опубликовавшем книгу под названием «Статистика», в которой приводилось описание политического устройства государств Европы.

случайные явления посредством обработки и анализа результатов наблюдений и измерений.
Любой

результат можно представить как совокупность значений, принятых в результате n опытов над какой-то с.в. или системой случайных величин.
Перед любой наукой ставятся в порядке возрастания сложности и важности следующие задачи:

собранных в результате наблюдений, специально поставленных опытов или произведенных измерений;
Разработать

методы анализа статистических сведений в зависимости от целей исследования.

банковская, таможенная статистика, платежный баланс и др.

Статистические службы международных организаций

Статистические службы организаций системы ООН;
Институт статистики ЮНЕСКО;
Статистический директорат Организации экономического сотрудничества и развития;
Статистическое бюро Европейских Сообществ и др.

и, как правило, систематический сбор данных о явлениях и процессах

общественной жизни путем регистрации заранее намеченных существенных признаков с целью получения в дальнейшем обобщающих характеристик этих явлений и процессов.
Статистическая совокупность – это множество единиц явления, объединенных в соответствии с задачей исследования единой качественной основой (однородностью), но отличающиеся друг от друга признаками.

из генеральной совокупности называют выборочной совокупностью или выборкой.
Количество элементов совокупности

- объем совокупности.
Способы отбора единиц совокупности:
повторный – объект перед отбором следующего возвращается в генеральную совокупность;
бесповторный – объект перед отбором следующего не возвращается в генеральную совокупность.

Основные понятия математической статистики

выборка должна быть репрезентативной – все объекты генеральной совокупности имеют одинаковую вероятность оказаться в выборке

группировки, называемые рядами распределения.
Статистические ряды распределения представляют собой упорядоченное расположение единиц

изучаемой совокупности на группы по группировочному признаку.
Различают атрибутивные и вариационные ряды распределения.
Атрибутивный – это ряд распределения, построенный по качественным признакам.
По количественному признаку строится вариационный ряд распределения.
В зависимости от характера вариации признака различают дискретные и интервальные (непрерывные) вариационные ряды распределения. 

Статистический ряд

9-0+1 = 10
Размах небольшой, значит можно составить вариационный ряд по

значениям.

ni – частоты
wi – относительные частоты
Fi* - накопленные относительные частоты

удобному для проведения анализа.

Группировка – это процесс образования однородных групп на основе расчленения статистической совокупности на части или объединения изучаемых единиц в частные совокупности по существенным признакам.
Оптимальное число групп можно определить по формуле Стерджесса: n = 1 + 3,322 x lg N,
где n - число групп
N - число единиц совокупности.
Величина равного интервала определяется по следующей формуле:

Сводка и группировка данных статистического наблюдения

степенные;
Средние структурные;
Средние хронологические.
Средние степенные
1. Средняя арифметическая.




В случае, если исходные данные

представлены в виде интервального ряда распределения, то в качестве вариантов усредняемого признака (хi) принимают середины интервалов, вычисляемые по каждой группе.

обычно применяется в тех случаях, когда варианты ряда представлены относительными

показателями динамики. Эта средняя выражает, как правило, средний темп относительного роста или спада.

(варианта), наиболее часто повторяющаяся в изучаемой совокупности. Мода отражает типичный,

наиболее распространенный вариант значения признака.
В дискретном ряду распределения мода – это варианта, которой соответствует наибольшая частота.
В интервальном ряду распределения сначала определяют модальный интервал (т.е. интервал, содержащий моду), которому соответствует наибольшая частота. Конкретное значение моды определяется формулой:

xMo – нижняя значение модального интервала;
i – величина модального интервала;
nMo – частота модального интервала;
nMo-1 – частота интервала, предшествующего модальному;
nMo+1 – частота интервала, следующего за модальным.

варианта, находящаяся в середине ранжированного ряда (варианта, делящая ранжированный ряд

пополам).
В дискретном ряду медианой является варианта, которой соответствует член кумулятивного ряда, впервые превысившая половину общей суммы частот.
В интервальном ряду распределения сначала необходимо определить медианный интервал (т.е. интервал, содержащий медиану). Медианным интервалом является тот, которому соответствует член кумулятивного ряда, впервые превысившая половину общей суммы частот. Затем работает формула:

Дисперсия
Можно отметить следующий недостаток этого показателя вариации – если варианты

xi имеют некоторую размерность (метр, рубль, килограмм и т.д.), то дисперсия имеет размерность в квадрате, что затрудняет ее интерпретацию (например, если средняя зарплата составляет 18 тысяч рублей, то соответствующая дисперсия может составить 500 тысяч рублей в квадрате, что лишено экономического смысла).

2. Среднее квадратическое отклонение

показатели вариации
Расчет относительных показателей вариации осуществляют как отношение абсолютного показателя

вариации к средней арифметической. Как правило, они рассчитываются в процентах.

Коэффициент вариации – это наиболее распространенный относительный показатель вариации. Считается, что если v>30%, то это говорит о большой вариации признака в изучаемой совокупности.

Стьюдента,
Пуассона,
нормальное распределение,
хи-квадрат распределение,

распределение Фишера,
биномиальное (распределение Бернулли),
равномерное распределение.

Характеристики и формы распределения

– закон Гаусса (ЗНР). Подчиненность закону нормального распределения тем точнее,

чем больше факторов действует вместе.
Нормальное распределение полностью определяется двумя входными параметрами: средней арифметической и среднеквадратическим отклонением (σ)

Нормальный закон распределения

Вид функции плотности нормального распределения вероятностей

Например, рост, вес людей (и не только), их физическая сила, умственные способности и т.д. Существует «основная масса» (по тому или иному признаку) и существуют отклонения в обе стороны.

вычисленная на основании опытных данных, является случайной величиной.

Точечные оценки параметров

распределения

Качество оценки характеризуется следующими свойствами:
Состоятельность: с ростом объема выборки оценка сходится по вероятности к параметру
Несмещенность: математическое ожидание совпадает с истинным значение оцениваемого параметра
Эффективность: дисперсия оценки меньше дисперсии любой другой оценки данного параметра

Среди всех нормально распределенных оценок наилучшей будет несмещенная эффективная оценка.

распределения близко к математическому ожиданию этого распределения. Закон больших чисел

важен, поскольку он гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.

Теоретическим обоснованием возможности экспериментального определения вероятностных характеристик является закон больших чисел

Смысл ЗБЧ: совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая

величины при стремлении количества выборок или количества её измерений (иногда

говорят — количества испытаний) к бесконечности.

Математическое ожидание случайной величины x обозначается M(x)

Математическое ожидание – это сумма произведений всех возможных значений случайной величины на вероятности этих значений.

Математическое ожидание – это в теории азартных игр сумма выигрыша, которую может заработать или проиграть игрок, в среднем, по каждой ставке. На языке азартных игроков это иногда называется «преимуществом игрока» (если оно положительно для игрока) или «преимуществом казино» (если оно отрицательно для игрока).

отклонения