xn(S)) – вектор признаков
y(S) – «основное свойство», класс
Дано:
S1, S2, …,
Sm, y(S1), y(S2), …, y(Sm) Найти:
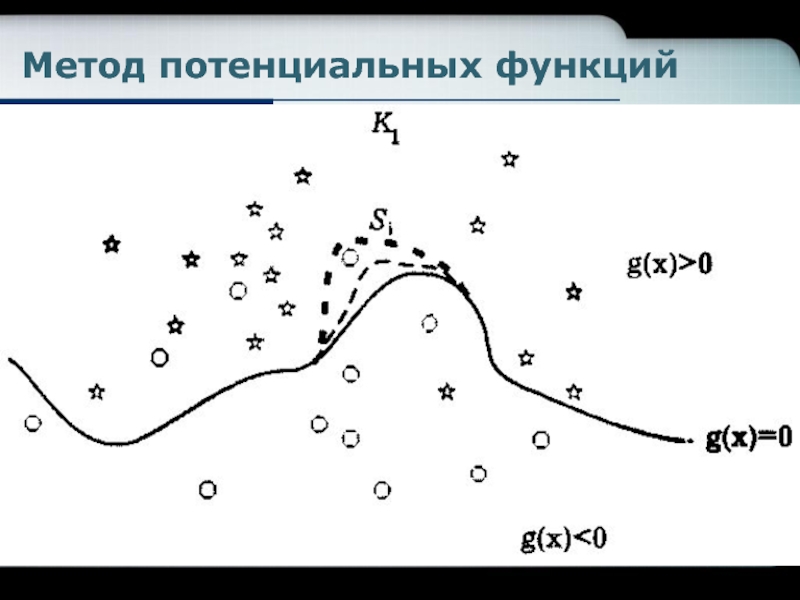
y(S) объекта S – задача распознавания
алгоритм – задача обучения