Сумма смежных углов равна180°. Вертикальные углы равны. Если две стороны и угол

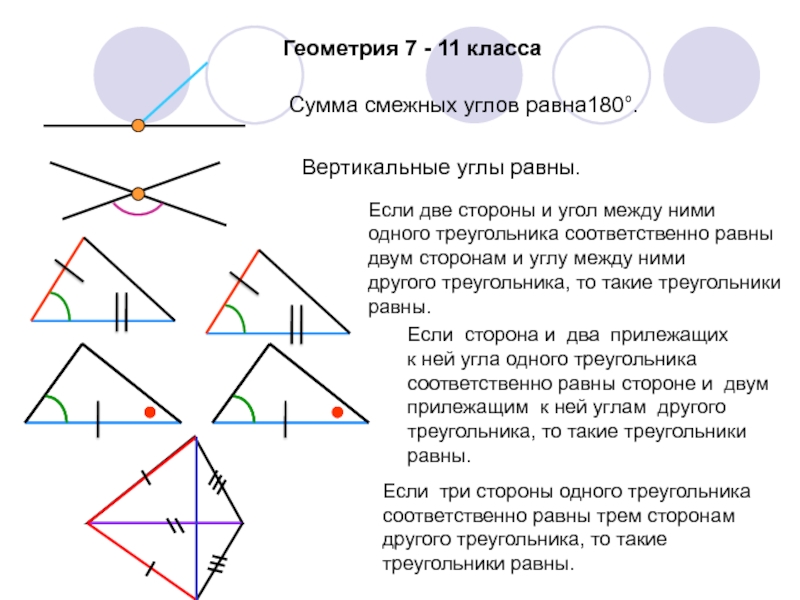
между ними
одного треугольника соответственно равны
двум сторонам и углу

Если сторона и два прилежащих
к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Геометрия 7 - 11 класса

высотой.
Углы при основании равнобедренного треугольника
равны.
Сумма углов треугольника равна 180°.

Внешний

Две прямые, параллельные третьей,
параллельны друг другу.

хорду пополам.
Центр окружности, описанной около треугольника,
является точкой пересечения перпендикуляров
к

Центр окружности, вписанной в треугольник,
является точкой пересечения его биссектрис.

Вписанный угол измеряется половиной дуги,
на которую он опирается.
 

точкой пересечения
делятся пополам.

Диагонали ромба пересекаются под прямым углом
и

Диагонали прямоугольника равны.

Квадрат имеет все вышеперечисленные свойства.

трапеции равна
полусумме оснований и параллельна им.
Если две параллельные прямые

Параллельные прямые, пересекающие две
данные прямые, отсекают на них
пропорциональные отрезки.

углам другого
треугольника.
Две стороны одного треугольника
пропорциональны двум сторонам

Квадрат стороны треугольника равен сумме
квадратов двух других сторон без удвоенного
произведения этих сторон на косинус угла
между ними.
c 2 = a 2 + b 2 – 2 b a • cosγ

Отношения сторон треугольника
к синусам противолежащих углов равны.

= 2R

S = a b

6) S = d 1 d 2

a
7) h S = (a + b) h
b

8) r S = p r



9) r S = r 2

не принадлежащая плоскости,
параллельна какой – нибудь прямой,
принадлежащей плоскости,

Если две пересекающиеся прямые
одной плоскости параллельны двум
пересекающимся прямым другой плоскости,
то эти плоскости параллельны.

ее проекции,
перпендикулярна и самой наклонной.
Если плоскость проходит через прямую,

Если прямая перпендикулярна двум
пересекающимся прямым плоскости, то она
перпендикулярна самой плоскости.

Две пересекающиеся прямые, параллельные
перпендикулярным прямым, перпендикулярны.

и ее проекцией на плоскость.
Углом между плоскостями называется угол
между прямыми,

S б.=

V =

V= S H

c2
Диагонали
параллелепипеда
пересекаются и точкой
пересечения делятся
пополам.
Противолежащие

высота
S = π R l,
R -радиус основания,
l –

V = π R2 H,

R -радиус основания,
H - высота

плоскость шара является
его плоскостью симметрии, а центр шара –

Касательная плоскость имеет с шаром
только одну общую точку – точку касания.