Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические модели в науке
Содержание
- 1. Математические модели в науке
- 2. Большую часть своих усилий человек тратит на
- 3. Математикам удалось разработать методы решения задач на
- 4. Следует различать также два вида задач на
- 5. Математические модели и их свойства Прежде чем
- 6. Иное дело, если возникающая задача затрагивает ключевые
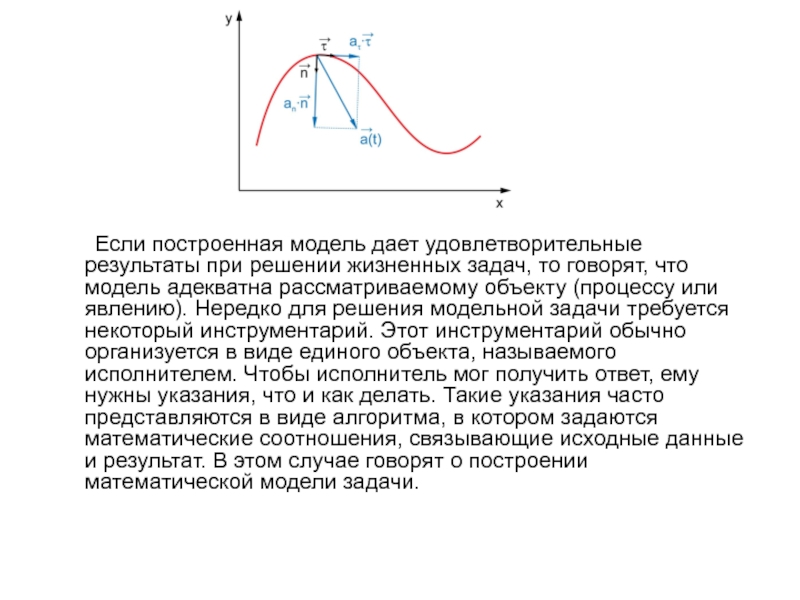
- 7. Если построенная модель дает удовлетворительные результаты при
- 8. Обычно модель возникает как необходимый этап решения
- 9. Обладая способностью представлять любую информацию в виде
- 10. Вообще выделяют три вида эксперимента (от лат. experimentum - проба, опыт): натурный, мысленный и математический.
- 11. Натурный эксперимент представляет манипуляцию с вещами и
- 12. Мысленный эксперимент - это также деятельность с
- 13. Математический эксперимент, имея дело не с самими
- 14. Пример 1Рассмотрим текст небольшой заметки из школьной
- 15. Если отбросить информацию, несущественную с точки зрения
- 16. Так как через первую трубу бассейн наполняется
- 17. Мы получили математическую модель, описывающую процесс наполнения
- 18. Пример 2На шоссе расположены пункты А и
- 19. Пример 3В обработку поступила партия из 150
- 20. Вводим в ячейки B3:D10 варианты возможного распила
- 21. В ячейках E11:H11 суммируем количество досок и
- 22. Даем команду Выполнить Машина выдает результаты Видно,
- 23. задания Постройте математические модели для приведеных ниже
- 24. Скачать презентанцию
Большую часть своих усилий человек тратит на поиск наилучшего т.е. оптимального решения поставленной задачи. Как, располагая определенными ресурсами, добиваться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной
Слайды и текст этой презентации
Слайд 3 Математикам удалось разработать методы решения задач на наибольшее и наименьшее
значение, или, как их еще называют, задач на оптимизацию (
от латинского “оптимум” – наилучший). Многие задачи, поиска оптимальных решений, могут быть решены только с использованием методов дифференциального исчисления. Ряд задач такого типа решается с помощью специальных методов линейного программирования, но существуют и такие экстремальные задачи, которые решаются средствами элементарной математики.Слайд 4 Следует различать также два вида задач на оптимизацию. В задачах
первого вида улучшение достигается за счет коренных качественных изменений: выбор
новых конструктивных решений, переход на новую технологию изготовления. В задачах второго рода качественная сторона дела остается неизменной, но меняются количественные показатели. В данной работе рассмотрены задачи только второго типа. В таких задачах ищутся наибольшее и наименьшее значения функций, зависящих от одной или нескольких переменных.Слайд 5Математические модели и их свойства
Прежде чем решать какую –
либо жизненную задачу, человек старается взвесить имеющуюся у него информацию,
выбрать из нее существенную. И только потом, когда станет более или менее ясно, из чего исходить и на какой результата рассчитывать, он приступает к решению задачи. Иногда описанный процесс называют “уяснением задачи”, фактически же это замена исходной жизненной задачи ее моделью. В осмыслении простейшей жизненной ситуации присутствует модельный подход, хотя человек обычно не замечает своей деятельности по созданию моделей – настолько она для него естественна.Слайд 6 Иное дело, если возникающая задача затрагивает ключевые моменты жизни одного
человека или какого – либо сообщества людей. Разнообразие информационных аспектов
в каждой такой задаче настолько велико, что бывает сложно из всего многообразия информации об изучаемом явлении или объекте выбрать наиболее существенные. В таких случаях необходимо сделать упрощающее предположение, чтобы выделить исходные данные, определить, что будет служить результатом и какова связь между исходными данными и результатом. Все это – предположения, исходные данные, результаты, связи между ними – их называют моделью задачи.Слайд 7 Если построенная модель дает удовлетворительные результаты при решении жизненных задач,
то говорят, что модель адекватна рассматриваемому объекту (процессу или явлению).
Нередко для решения модельной задачи требуется некоторый инструментарий. Этот инструментарий обычно организуется в виде единого объекта, называемого исполнителем. Чтобы исполнитель мог получить ответ, ему нужны указания, что и как делать. Такие указания часто представляются в виде алгоритма, в котором задаются математические соотношения, связывающие исходные данные и результат. В этом случае говорят о построении математической модели задачи.Слайд 8Обычно модель возникает как необходимый этап решения конкретной задачи. Однако
в дельнейшем может происходить обособление модели от задачи, и модель
начинает жить самостоятельно. Примером может служить сюжет движения с постоянной скоростью, который возникал в человеческой деятельности столь часто, что в конце концов обособился от задач и стал составляющей физического знания, называемого “равномерное прямолинейное движение”. Теперь при необходимости решить какую – либо задачу, связанную с равномерным движением пользуются этой готовой моделью процесса. В одних задачах результатом может оказаться время, в других – пройденный путь, в третьих скорость. Остальные параметры модели процесса станут исходными данными.Слайд 9Обладая способностью представлять любую информацию в виде количественных характеристик, математика
вырабатывает и особые, отличные от естествознания приемы исследования - математический
эксперимент, математическая гипотеза, математическое моделирование. Их специфика состоит в том, ч о вместо операций с веществом и энергией они добывают результат путем решения соответствующих дифференциальных уравнений, интерпретируя затем полученные числовые выражения в терминах содержательного значения.Слайд 10Вообще выделяют три вида эксперимента (от лат. experimentum - проба,
опыт): натурный, мысленный и математический.
Слайд 11 Натурный эксперимент представляет манипуляцию с вещами и энергиями. Он осуществляется
в контролируемых и управляемых условиях, обычно специально созданных.
Слайд 12Мысленный эксперимент - это также деятельность с материальными предметами и
процессами, но взятыми не в натуре, а на уровне образного
прочтения физической ситуации и в значительной мере, как считает Р. Харре, опираясь на интуицию64. Так, Г. Галилей, рассуждая о возможности физических изменений систем, движущихся относительно других систем, провел мысленный эксперимент. "Наполнив" каюту корабля бабочками, мухами и т.п., стал "наблюдать" их поведение с целью определить разницу в состояниях, когда корабль плывет и когда он находится в покое.Слайд 13Математический эксперимент, имея дело не с самими предметами и процессами
природы, а с их количественными описаниями, позволяет избежать материальных затрат
на сооружение установок и лабораторий, ибо, как заметил отечественный геометр А. Яглом, единственной лабораторией математика является его интеллект.Слайд 14Пример 1
Рассмотрим текст небольшой заметки из школьной стенгазеты:
После капитального ремонта
бассейн «Дельфин» буквально преобразился: просторные раздевалки и душевые сверкают новеньким
кафелем, захватывает дух от вида замысловатой горки и пятиметровой вышки, манит голубая гладь водных дорожек. Но самое главное, строители переделали систему водоснабжения бассейна. Раньше бассейн наполнялся водой из одной трубы. На это уходило 30 часов. Теперь строители подвели еще одну трубу, которая наполняет бассейн за 20 часов. Представляете, как мало времени теперь потребуется для наполнения бассейна, если включить обе эти трубы!Слайд 15Если отбросить информацию, несущественную с точки зрения поставленной задачи, то
условие задачи можно сформулировать так:
Через первую трубу бассейн наполняется за
30 часов, через вторую трубу — за 20 часов. За сколько часов бассейн наполнится через обе трубы?Попробуем решить задачу в общем виде, обозначив время заполнения бассейна через первую и вторую трубы А и В соответственно. Примем за 1 весь объем бассейна, искомое время обозначим через t.
Слайд 16Так как через первую трубу бассейн наполняется за А часов,
то 1/A - часть бассейна, наполняемая первой трубой за
1 час; 1/B -часть бассейна, наполняемая второй трубой за 1 час.Следовательно, скорость наполнения бассейна первой и второй трубами вместе составит: 1/A + 1/B .
Можем записать:
(1)
Мы получили математическую модель, описывающую процесс наполнения бассейна из двух труб.
Слайд 17Мы получили математическую модель, описывающую процесс наполнения бассейна из двух
труб.
Преобразуем выражение:
Формула (1) примет вид:
(2)Теперь искомое время может быть вычислено по формуле:
Несложно подсчитать, что при исходных данных А = 30 и В = 20 искомое время равно 12 часам.
Слайд 18Пример 2
На шоссе расположены пункты А и В, удаленные друг
от друга на 20 км. Мотоциклист выехал из пункта В
в направлении, противоположном А, со скоростью 50 км/ч.Составим математическую модель, описывающую положение мотоциклиста относительно пункта А через t часов.
За t часов мотоциклист проедет 50* t км и будет находиться от А на расстоянии 50* t км + 20 км. Если обозначить буквой s расстояние (в километрах) мотоциклиста до пункта А, то зависимость этого расстояния от времени движения можно выразить формулой:
s = 50*t + 20 , где t > 0.
Слайд 19Пример 3
В обработку поступила партия из 150 досок длиной по
7.5 м. каждая, для изготовления комплектов из 4-х деталей. Комплект
состоит из:1 детали длиной 3 м.
2-х деталей длиной 2 м.
1 детали длиной 1.5 м
Как распилить все доски, получив наибольшее возможное число комплектов?
Решение.
Для решения этой задачи воспользуемся редактором электронных таблиц EXCEL
Слайд 20Вводим в ячейки B3:D10 варианты возможного распила одной доски. В
ячейках E3:E10 ставим по умолчанию количество досок по одной. В
ячейках F3:H10 суммируем получившиеся распиленные детали.Слайд 21В ячейках E11:H11 суммируем количество досок и деталей.
Вводим формулы:
G11 - ABS(2*F11-G11)
G12 - ABS(G11-2*H11)
G13 - ABS(F11-H11)
Входим
во встроенную функцию EXCEL Поиск Решения Устанавливаем Целевую ячейку E11
Ставим ограничения:
E3:E10=>0
E3:E10= ЦЕЛЫЕ
G12<=1
G13<=1
G14<=1
Слайд 22Даем команду Выполнить
Машина выдает результаты
Видно, что для полных
127 комплектов не хватает одной двухметровой детали.
То есть максимальное
число комплектов – 126. Остаток – по одной детали всех типов. Ответ: максимальное число комплектов – 126
Слайд 23задания
Постройте математические модели для приведеных ниже задач. Какой вы
можете сделать вывод на основании полученных моделей?
а) Первая бригада может
выполнить задание за А дней, а вторая — за В дней. За сколько дней обе бригады выполнят задание, работая вместе?б) Два велосипедиста одновременно направились навстречу друг другу из двух сел. Первый мог бы проехать расстояние между селами за А минут, второй — за В минут. Через сколько минут они встретятся?
в) Из пункта А в пункт F ведет прямолинейная дорога длиной 35 км. Остановки автобуса расположены в точках В, С, D, Е. Известно, что АС = 12 км, BD = 11 км, СЕ = 12 км, DF = 16 км. Найдите расстояния: АВ, ВС, CD, DE и EF.