Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое моделирование физических процессов и систем 1 Андрей Алексеевич
Содержание
- 1. Математическое моделирование физических процессов и систем 1 Андрей Алексеевич
- 2. Инфокоммуникационные технологии и системы связиЗнания в области
- 3. SDRОдна из первых систем ПОР разрабатывалась американскими
- 4. SDRЦитата из статьи на habrhabr.ru «Software Defined
- 5. SDRЧто имеем сегодня? - https://youtu.be/cygDXeZaiOM«Радиотехника — это
- 6. МатематикаМатематические действия и использование их в цифровой
- 7. МатематикаМатематические действия и использование их в цифровой
- 8. МатематикаМатематические действия и использование их в цифровой
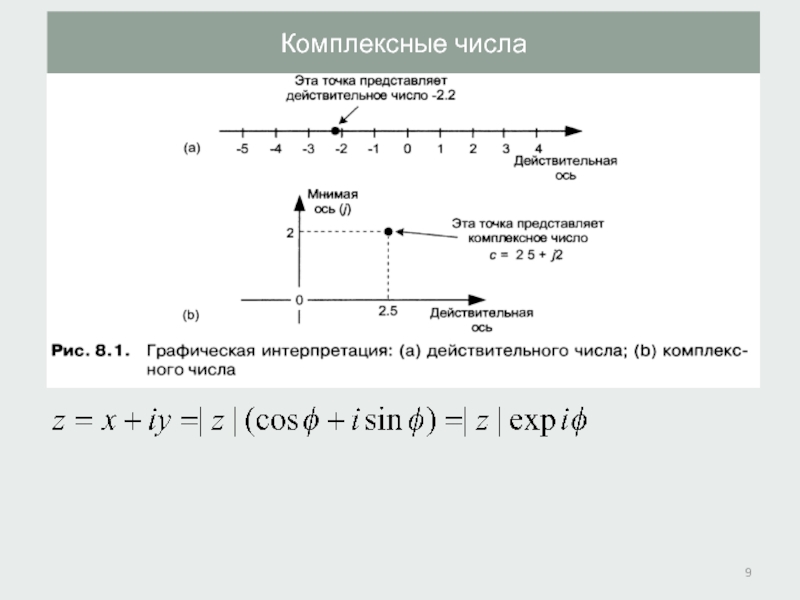
- 9. Комплексные числа
- 10. Комплексные числа
- 11. Модель цифрового SDR приемника
- 12. Модель цифрового SDR приемника
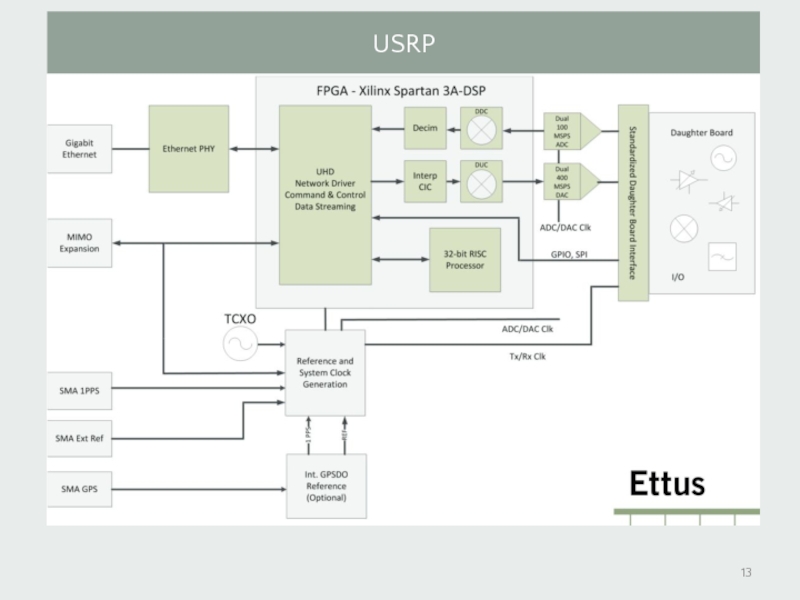
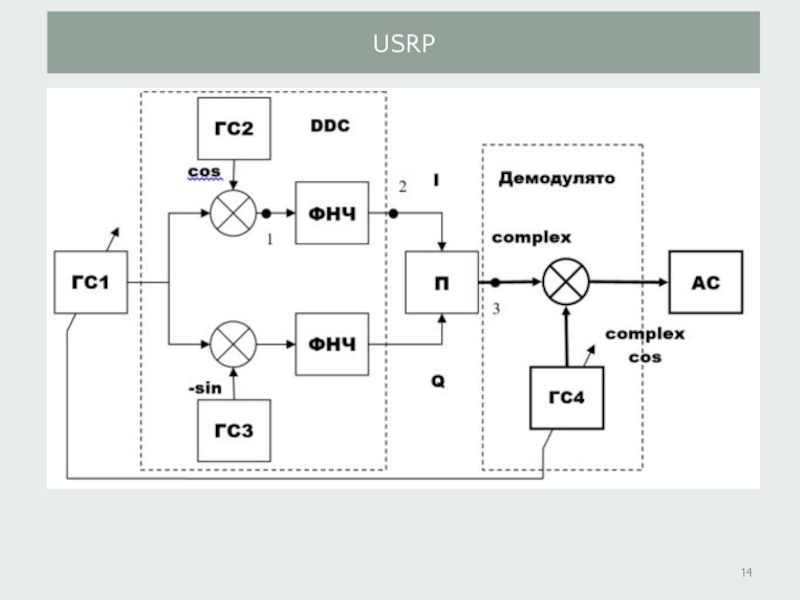
- 13. USRP
- 14. USRP
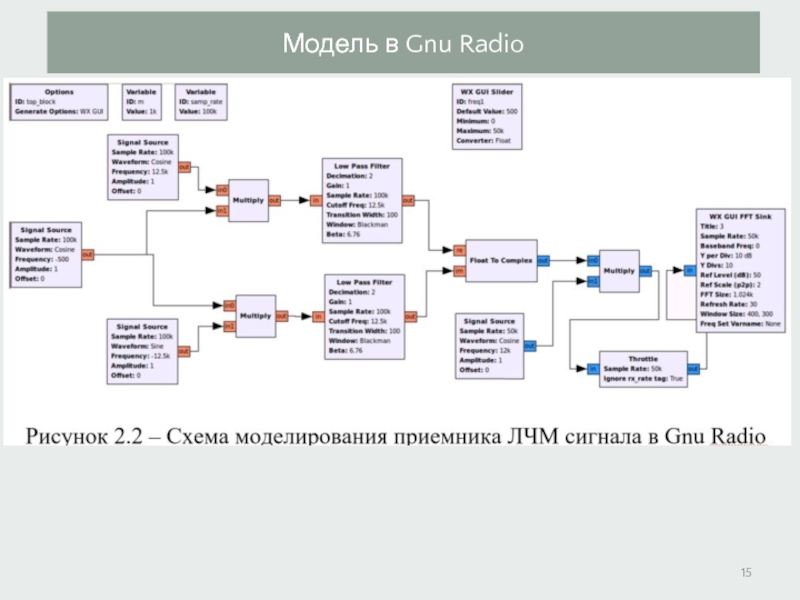
- 15. Модель в Gnu Radio
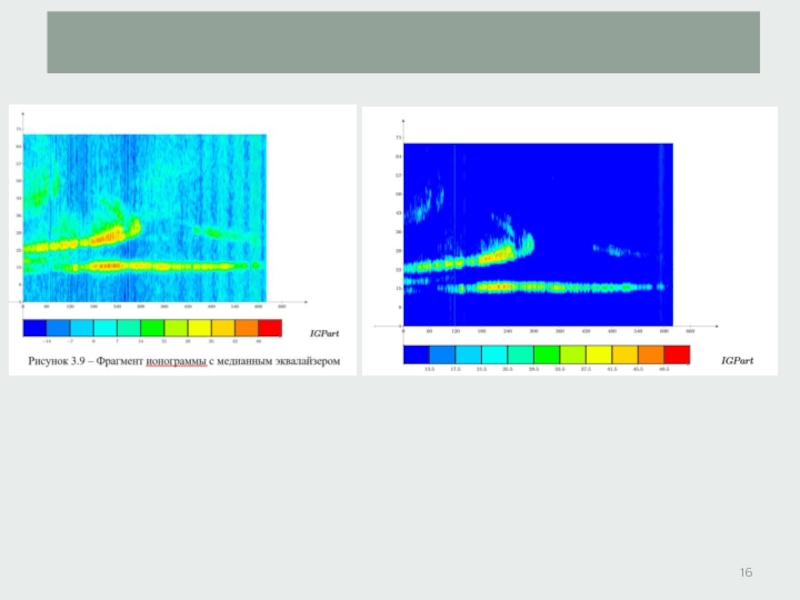
- 16. Слайд 16
- 17. Связь математики с инфокоммуникациямиПодробнее о проблемах разработки математических моделей http://habrahabr.ru/post/256713/
- 18. 1. Математическое моделирование. Форма и принципы представления
- 19. 1. Математическое моделирование. Форма и принципы представления математических моделейАБАБ
- 20. Все модели можно разделить на два класса:вещественные,идеальные.Вещественные
- 21. Вещественные натурные модели - реальные объекты, процессы
- 22. Идеальные наглядные модели - схемы, карты, чертежи,
- 23. Математическое моделирование ставит в соответствие моделируемому физическому
- 24. В общем случае математическая модель реального объекта, процесса или
- 25. По принципам построения математические модели разделяют на:- аналитические; имитационные.Аналитическая модель
- 26. В имитационном моделировании функционирование объектов, процессов или систем описывается
- 27. В зависимости от характера исследуемых реальных процессов
- 28. Особенности построения математических моделей
- 29. Для построения математической модели необходимо:тщательно проанализировать реальный
- 30. Математическое моделирование, кроме исследования объекта, процесса или
- 31. На этапе выбора математической модели устанавливаются: линейность
- 32. Построение математической модели обычно начинается с построения
- 33. Наиболее простой случай - хорошо известны законы,
- 34. Основным критерием истинности (применимости некоторой математической модели
- 35. Компьютерное моделирование и вычислительный эксперимент
- 36. Компьютерное моделирование основывается на:построении математических моделей для описания
- 37. Для проверки адекватности математической модели и реального
- 38. В задачах проектирования или исследования поведения реальных
- 39. Второй этап решения прикладной задачи – поиск или разработка
- 40. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математическое моделирование физических процессов и систем
Андрей Алексеевич Чернов
к.т.н., доцент
кафедры РТиС
Слайд 2Инфокоммуникационные технологии и системы связи
Знания в области компьютерных наук и
телекоммуникаций, а также готовность выполнять исследования и разработки средств генерации,
передачи, приема, обработки информации.Программно-определяемая радиосистема (англ. Software-defined radio, SDR) — радиопередающая или радиоприемная система, позволяющая с помощью программного обеспечения устанавливать или изменять рабочие радиочастотные параметры, включая, в частности, диапазон частот, тип модуляции или выходную мощность, за исключением изменения рабочих параметров, используемых в ходе обычной предварительно определенной работы с предварительными установками радиоустройства, согласно той или иной спецификации или системы.
Слайд 3SDR
Одна из первых систем ПОР разрабатывалась американскими военными.
Цель проекта
- использование программной обработки для эмуляции более 10 существующих военных
радиосистем.Вторичная цель - возможность поддержки любых новых схем кодирования и модуляции, чтобы военные могли использовать более совершенные модуляции и кодирования.
Слайд 4SDR
Цитата из статьи на habrhabr.ru «Software Defined Radio (SDR)»:
Суть технологии
SDR Вообще говоря — очень круто, что математика дала нам возможность
вот так вот запросто двигать спектр туда сюда ... Наши деды — для извлечения информации делали всякие аналоговые схемы, которые делали нужное нам математическое преобразование, типа такой:Слайд 5SDR
Что имеем сегодня? - https://youtu.be/cygDXeZaiOM
«Радиотехника — это экспериментальная математика». Схемы
выполняют над сигналами различные математические действия.
Только аппаратная реализация радиотехнических
устройств не позволяет изменять их функциональные возможности и для реализации новых функций необходима разработка новых аппаратных средств, требующая больших затрат времени. Слайд 6Математика
Математические действия и использование их в цифровой связи:
Децимация – это
дискретизация с частотой много меньше одной четверти частоты Найквиста (либо
много меньше половины частоты сигнала). Например, если частота сигнала 100 МГц, то минимальная необходимая частота дискретизации составляет 200 МГц. Поэтому данный физический сигнал должен быть оцифрован с частотой меньше 50 МГц.Интерполяция – это дискретизация с частотой большей, чем необходимая для выполнения критерия Найквиста. Сигнал с полосой 5 МГц может быть интерполирован с любой частотой больше 10 МГц. Интерполяция является обратным децимации процессом, но выполнить его гораздо сложнее.
Слайд 7Математика
Математические действия и использование их в цифровой связи:
Совместная децимация и
интерполяция – используется в том случае, если необходимо получить дробный
коэффициент преобразования частоты.Усреднение сигналов – используется для улучшения качества принимаемого сигнала. Выполнение данной функции возможно в том случае, если дискретизация сигнала намного выше его скорости, так как усреднение предусматривает накопление нескольких последовательных отсчетов.
Уменьшение шума квантования АЦП – помогает улучшить качество цифрового сигнала. Обычно используется два алгоритма: сверхдискретизация и рандомизация (или размывание).
Слайд 8Математика
Математические действия и использование их в цифровой связи:
Удаление постоянной составляющей.
Перенос
частоты с помощью прореживания.
Автоматическая регулировка усиления.
Фильтрация сигналов.
Демодуляция сигналов.
Комплексные числа.
Слайд 17Связь математики с инфокоммуникациями
Подробнее о проблемах разработки математических моделей http://habrahabr.ru/post/256713/
Слайд 181. Математическое моделирование. Форма и принципы представления математических моделей
Моделирование -
замещение некоторого объекта А другим объектом Б
объект А - оригинал
или объект моделирования;замещающий Б – модель.
Модель - объект-заменитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала
Цель моделирования - получение, обработка, представление и использование информации об объектах, которые взаимодействуют между собой и внешней средой; модель выступает как средство познания свойств и закономерностей поведения объекта-оригинала.
А
Б
Слайд 20Все модели можно разделить на два класса:
вещественные,
идеальные.
Вещественные модели:
натурные,
физические,
математические.
Идеальные модели:
наглядные,
знаковые,
математические.
1. Математическое
моделирование. Форма и принципы представления математических моделей
Слайд 21Вещественные натурные модели - реальные объекты, процессы и системы, над
которыми выполняются эксперименты научные, технические и производственные.
Вещественные физические модели -
макеты, муляжи, воспроизводящие физические свойства оригиналов (кинематические, динамические, гидравлические, тепловые, электрические, световые модели).Вещественные математические - аналоговые, структурные, геометрические, графические, цифровые и кибернетические модели.
1. Математическое моделирование. Форма и принципы представления математических моделей
Слайд 22Идеальные наглядные модели - схемы, карты, чертежи, графики, графы, аналоги,
структурные и геометрические модели.
Идеальные знаковые модели - символы, алфавит, языки программирования,
упорядоченная запись, топологическая запись, сетевое представление.Идеальные математические модели - аналитические, функциональные, имитационные, комбинированные модели.
1. Математическое моделирование. Форма и принципы представления математических моделей
Слайд 23Математическое моделирование ставит в соответствие моделируемому физическому процессу систему математических
соотношений. Решение соотношений позволяет получить ответ на вопрос о поведении
объекта без создания физической модели.Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала.
Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.
1. Математическое моделирование. Форма и принципы представления математических моделей
Слайд 24В общем случае математическая модель реального объекта, процесса или системы представляется в
виде системы функционалов
Фi (X,Y,Z,t)=0
где X - вектор входных переменных, X=[x1,x2,x3, ... , xN]t,
Y - вектор выходных переменных, Y=[y1,y2,y3,
... , yN]t,Z - вектор внешних воздействий, Z=[z1,z2,z3, ... , zN]t,
t - координата времени.
Построение математической модели заключается в определении связей между теми или иными процессами и явлениями, создании математического аппарата, позволяющего выразить количественно и качественно связь между теми или иными процессами и явлениями, между интересующими специалиста физическими величинами, и факторами, влияющими на конечный результат.
1. Математическое моделирование. Форма и принципы представления математических моделей
Слайд 25По принципам построения математические модели разделяют на:
- аналитические;
имитационные.
Аналитическая модель в зависимости от
математической проблемы:
- уравнения (алгебраические, трансцендентные, дифференциальные, интегральные),
- аппроксимационные задачи (интерполяция,
экстраполяция, численное интегрирование и дифференцирование),- задачи оптимизации,
- стохастические проблемы.
1. Математическое моделирование. Форма и принципы представления математических моделей
Слайд 26В имитационном моделировании функционирование объектов, процессов или систем описывается набором алгоритмов.
Алгоритмы
имитируют реальные элементарные явления, составляющие процесс или систему с сохранением
их логической структуры и последовательности протекания во времени.Имитационное моделирование позволяет по исходным данным получить сведения о состояниях процесса или системы в определенные моменты времени, однако прогнозирование поведения объектов, процессов или систем здесь затруднительно.
1. Математическое моделирование. Форма и принципы представления математических моделей
Слайд 27В зависимости от характера исследуемых реальных процессов и систем математические модели могут
быть:
- детерминированные,
- стохастические.
1. Математическое моделирование. Форма и принципы представления математических
моделейСлайд 29Для построения математической модели необходимо:
тщательно проанализировать реальный объект или процесс;
выделить
его наиболее существенные черты и свойства;
определить переменные, т.е. параметры, значения
которых влияют на основные черты и свойства объекта;описать зависимость основных свойств объекта, процесса или системы от значения переменных с помощью логико-математических соотношений (уравнения, равенства, неравенства, логико-математические конструкций);
выделить внутренние связи объекта, процесса или системы с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций;
определить внешние связи и описать их с помощью ограничений, уравнений, равенств, неравенств, логико-математических конструкций.
1. Процесс построения математической модели. Алгоритм процесса.
Слайд 30Математическое моделирование, кроме исследования объекта, процесса или системы и составления
их математического описания, также включает:
построение алгоритма, моделирующего поведение
объекта, процесса или системы;проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента;
корректировка модели;
использование модели.
Математическое описание исследуемых процессов и систем зависит от:
природы реального процесса или системы и составляется на основе законов физики, электротехники, механики, термодинамики, гидродинамики, теории пластичности, теории упругости и т.д.
требуемой достоверности и точности изучения и исследования реальных процессов и систем.
1. Процесс построения математической модели. Алгоритм процесса.
Слайд 31На этапе выбора математической модели устанавливаются:
линейность и нелинейность объекта,
процесса или системы,
динамичность или статичность,
стационарность или нестационарность,
степень детерминированности
исследуемого объекта или процесса. Математическая модель никогда не бывает полностью тождественна рассматриваемому объекту, процессу или системе.
Она является приближенным описанием. Поэтому результаты, полученные при анализе модели, носят приближенный характер.
Их точность определяется степенью адекватности (соответствия) модели и объекта.
1. Процесс построения математической модели. Алгоритм процесса.
Слайд 32Построение математической модели обычно начинается с построения и анализа простейшей,
наиболее грубой математической модели рассматриваемого объекта, процесса или системы. В
дальнейшем, в случае необходимости, модель уточняется, делается ее соответствие объекту более полным.Пример. Нужно определить площадь поверхности письменного стола.
Реальный объект (поверхность стола) заменяется абстрактной математической моделью – прямоугольником.
Прямоугольнику приписываются размеры, полученные в результате измерения длины и ширины поверхности стола, и площадь такого прямоугольника приближенно принимается за искомую площадь стола.
1. Процесс построения математической модели. Алгоритм процесса.
Слайд 33 Наиболее простой случай - хорошо известны законы, определяющие поведение и
свойства объекта, процесса или системы + имеется большой практический опыт
их применения.Более сложная ситуация - наши знания об изучаемом объекте, процессе или системе недостаточны.
В этом случае при построении математической модели приходится делать дополнительные предположения, (гипотезы), - модель называется гипотетической.
В результате исследования гипотетической модели выводы носят условный характер.
Для проверки выводов необходимо сопоставить результаты исследования модели на ЭВМ с результатами натурного эксперимента.
1. Процесс построения математической модели. Алгоритм процесса.
Слайд 34 Основным критерием истинности (применимости некоторой математической модели к изучению рассматриваемого
объекта, процесса или системы) является эксперимент, практика.
Построение математической модели в
прикладных задачах – один из наиболее сложных этапов работы. Во многих случаях правильно выбрать модель –решить проблему более, чем наполовину.
Трудность данного этапа - требуется соединения математических и специальных знаний.
Поэтому для успешного решения прикладных задач важно, чтобы математики обладали бы специальными знаниями об объекте, а специалисты – знаниями математики, знанием ЭВМ и программирования.
1. Процесс построения математической модели. Алгоритм процесса.
Слайд 36Компьютерное моделирование основывается на:
построении математических моделей для описания изучаемых процессов;
использовании новейших
вычислительных машин, обладающих высоким быстродействием и способных вести диалог с
человеком.Суть компьютерного моделирования: на основе математической модели с помощью ЭВМ проводится серия вычислительных экспериментов, т.е. исследуются свойства объектов или процессов, находятся их оптимальные параметры и режимы работы, уточняется модель.
Вычислительный эксперимент позволяет заменить дорогостоящий натурный эксперимент расчетами на ЭВМ.
1. Компьютерное моделирование. Методы решения математических задач.
Слайд 37
Для проверки адекватности математической модели и реального объекта, процесса или
системы результаты исследований на ЭВМ сравниваются с результатами эксперимента на
опытном натурном образце.Компьютерное моделирование и вычислительный эксперимент позволяют свести исследование "нематематического" объекта к решению математической задачи.
1. Компьютерное моделирование. Методы решения математических задач.
Слайд 38В задачах проектирования или исследования поведения реальных объектов, процессов или
систем чаще всего используются математические модели типа ДНА:
Д – модель
детерминированная, отсутствует (не учитывается) влияние случайных процессов.Н – модель непрерывная, информация и параметры непрерывны.
А – модель аналитическая, функционирование модели описывается в виде уравнений (линейных, нелинейных, систем уравнений, дифференциальных и интегральных уравнений).
1. Компьютерное моделирование. Методы решения математических задач.
Слайд 39Второй этап решения прикладной задачи – поиск или разработка метода решения сформулированной
математической задачи.
Все методы решения математических задач можно разделить на 2
группы:точные методы решения задач, когда решения математических задач ответ удается получить в виде формул
численные методы решения задач, в которых решение сложных математических задач сводится к последовательному выполнению большого числа простых арифметических операций. Непосредственная разработка численных методов относится к вычислительной математике.
1. Компьютерное моделирование. Методы решения математических задач.