Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Маслов Евгений Анатольевич доц., к.ф.-м.н. Кафедра
Содержание
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Маслов Евгений Анатольевич доц., к.ф.-м.н. Кафедра
- 2. Слайд 2
- 3. СОДЕРЖАНИЕОБЩИЕ СВЕДЕНИЯ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ 3. ЛИНЕЙНАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ4. АЛГОРИТМ РЕШЕНИЯСПИСОК ЛИТЕРАТУРЫ2
- 4. 1. ОБЩИЕ СВЕДЕНИЯ3 ВВЕДЕНИЕ Теплопередача, или теплообмен –
- 5. 2. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ Нестационарный перенос тепла теплопроводностью описывается
- 6. 3. ЛИНЕЙНАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ ОДНОМЕРНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ В качестве
- 7. ПРОДОЛЖЕНИЕ 6(2)(3)(4)(5)
- 8. ПРОДОЛЖЕНИЕ Эту задачу в полной математической постановке
- 9. ПРОДОЛЖЕНИЕ Тогда с учетом приведенных обозначений значение
- 10. ПРОДОЛЖЕНИЕ 9 Выбранную схему аппроксимации ● и
- 11. ПРОДОЛЖЕНИЕ10 Рис. 3 наглядно демонстрирует, что используется
- 12. ПЕРЕРЫВ
- 13. ПРОДОЛЖЕНИЕ11 Составим СЛАУ для первого временного слоя
- 14. ПРОДОЛЖЕНИЕ12 На левой границе × (i=0) используя
- 15. ПРОДОЛЖЕНИЕ13 Результат решения СЛАУ (15) – (17) с
- 16. ПРОДОЛЖЕНИЕ14 Составим СЛАУ для второго временного слоя
- 17. ПРОДОЛЖЕНИЕ15 На левой границе × (i=0) используя
- 18. ПРОДОЛЖЕНИЕ16 Сравнивая значения коэффициентов ai, bi, ci,
- 19. 4. АЛГОРИТМ РЕШЕНИЯ17 1. Задание входных данных
- 20. ПРОДОЛЖЕНИЕ18 5. Начать основную программу с оператора:
- 21. ПРОДОЛЖЕНИЕ19 10. Произвести вычисление температуры в каждый
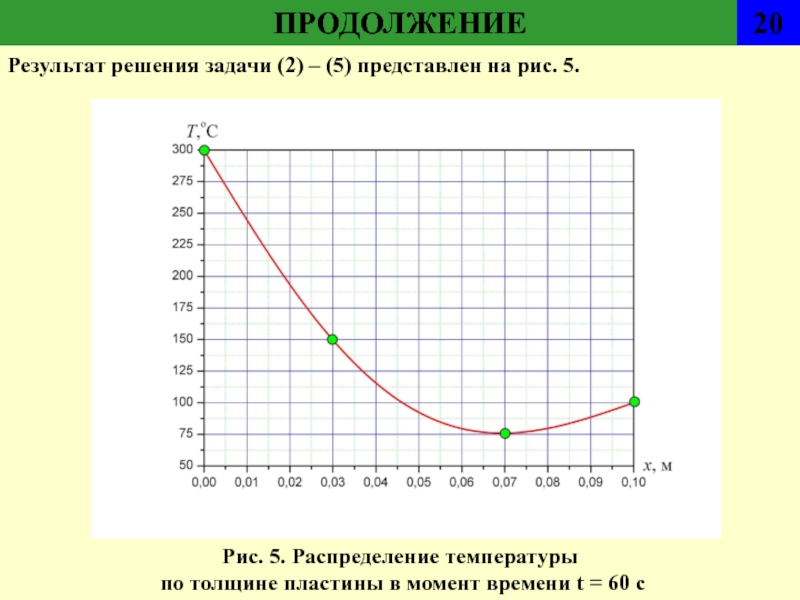
- 22. ПРОДОЛЖЕНИЕ20 Рис. 5. Распределение температуры по
- 23. ЛИТЕРАТУРА Кузнецов Г.В., Шеремет М.А. разностные методы
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Маслов Евгений Анатольевич
доц., к.ф.-м.н.
Кафедра атомных и тепловых электростанций
Корпус 4,
ауд 234
Слайд 3СОДЕРЖАНИЕ
ОБЩИЕ СВЕДЕНИЯ
УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
3. ЛИНЕЙНАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ
4. АЛГОРИТМ РЕШЕНИЯ
СПИСОК ЛИТЕРАТУРЫ
2
Слайд 41. ОБЩИЕ СВЕДЕНИЯ
3
ВВЕДЕНИЕ
Теплопередача, или теплообмен – это учение о
самопроизвольных необратимых процессах распределения (переноса) теплоты в пространстве с неоднородным
полем температуры.Сложный процесс переноса теплоты разбивают на ряд более простых: теплопроводность, конвекция и теплообмен излучением. Различают молекулярный и конвективный механизмы переноса теплоты.
Молекулярный перенос теплоты (диффузия) осуществляется посредством теплового движения микрочастиц в среде с неоднородным распределением температуры.
Конвективный перенос теплоты осуществляется в среде с неоднородным распределением скорости и температуры макроскопическими элементами среды при их перемещении.
Теплопроводностью (кондуктивный) называют молекулярный перенос теплоты в сплошной среде, обусловленный наличием градиента температуры (закон Фурье).
Слайд 52. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
Нестационарный перенос тепла теплопроводностью описывается следующим уравнением, записанным
в декартовой системе координат:
Это уравнение устанавливает связь между временным и
пространственным изменением температуры в любой точке тела. Здесь ρ – плотность (кг/м3), с – удельная теплоемкость (Дж/(кг·ºС)), λ – коэффициент теплопроводности (Вт/(м·ºС)), T – температура (ºС), x, y – декартовы координаты (м), t – время (с), Qw(x, y, t, T) – мощность внутренних источников тепловыделения (Вт/м3).Уравнение (1) описывает множество вариантов развития процесса кондуктивного теплопереноса (теплопроводности). Чтобы из большого количества этих вариантов выбрать один и дать его полное математическое описание, к соотношению (1) необходимо добавить условия однозначности, которые содержат геометрические, физические, начальные и граничные условия (см. лекцию 2).
4
(1)
Слайд 63. ЛИНЕЙНАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ
ОДНОМЕРНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
В качестве примера применения метода
конечных разностей (МКР) рассмотрим краевую задачу на основе одномерного уравнения
теплопроводности. Анализируется теплопередача через плоскую бесконечную пластину или изолированный стержень (рис. 1). На одной границе пластины поддерживается постоянная температура TL=300°C, на другой границе - температура TR=100°C. Начальная температура равна T0=20°C, источники тепловыделения внутри пластины отсутствуют.Рис. 1. Геометрия рассматриваемой задачи
5
Слайд 8ПРОДОЛЖЕНИЕ
Эту задачу в полной математической постановке будем решать МКР
на равномерной сетке. Для этого разобьем пластину по толщине на
Nx равных промежутков, т.е. построим конечно-разностную сетку (рис. 2):Рис. 2. Конечно-разностная сетка:
○ – координаты внутренних узлов;
× – координаты граничных узлов
Для аппроксимации дифференциального уравнения (2) разностным методом введем пространственно–временную сетку с координатами xi = i·hx, tk = k∙τ, где hx – шаг по пространству, τ – шаг по времени. При этом i=0…Nx, k=0…Nt.
где Lx – длина области решения [м] и Time – время протекающего процесса [c] (задаются пользователем). Nx и Nt – количество шагов по пространству и времени (задаваемые пользователем целые числа).
7
Слайд 9ПРОДОЛЖЕНИЕ
Тогда с учетом приведенных обозначений значение температуры в узлах
запишется следующим образом T(xi, tk) = Tik.
Далее заменим дифференциальные операторы
в (2) на их конечно-разностные аналоги. Будем использовать неявную схему, которая является абсолютно устойчивой.В результате аппроксимации частных производных соответствующими конечными разностями (6) получаем следующую систему линейных алгебраических уравнений (СЛАУ):
Полученная СЛАУ замыкается аппроксимируемыми начальным (8) и граничными условиями (9) и (10):
8
(6)
(7)
(8)
(9)
(10)
Слайд 10ПРОДОЛЖЕНИЕ
9
Выбранную схему аппроксимации ● и ● частных производных
можно представить графически следующим образом:
Рис. 3. Шаблон неявной четырехточечной разностной
схемы:
○ – координаты внутренних узлов;
● – координаты узлов в начальный момент времени;
×, × – координаты граничных узлов левой и правой границ соответственноСлайд 11ПРОДОЛЖЕНИЕ
10
Рис. 3 наглядно демонстрирует, что используется четырехточечная разностная схема
- три точки берутся на новом временном слое ● и
одна со старого временного слоя ●.Сформулированный выше способ аппроксимации производных называется неявным потому, что поле температуры на новом временном слое представлено неявно, т.е. для его определения необходимо решать систему уравнений (7) – (10) полинейно вдоль горизонтальных линий используя метод прогонки.
Приведем аппроксимированное уравнение теплопроводности (7) к виду (11) путем элементарных алгебраических преобразований
Тогда, получим следующие коэффициенты
(11)
(12)
(13)
Слайд 13ПРОДОЛЖЕНИЕ
11
Составим СЛАУ для первого временного слоя k=1 для всех
узлов i=0…Nx используя выражение (11).
Выпишем значения коэффициентов ai, bi, ci,
di (i=0…Nx) входящих в СЛАУ (14) с учетом выражений (8), (9), (10) и (13)(14)
Слайд 14ПРОДОЛЖЕНИЕ
12
На левой границе × (i=0) используя аппроксимированное граничное условие
(9):
Внутри области решения ○ (i=1…Nx – 1 ) используя коэффициенты
аппроксимированного уравнения теплопроводности (13): где значения температуры в начальный момент времени (k=0) в узлах ● известны из начального условия (8):
На правой границе × (i=0) используя аппроксимированное граничное условие (10):
(15)
(16)
(17)
Слайд 15ПРОДОЛЖЕНИЕ
13
Результат решения СЛАУ (15) – (17) с учетом (8) является
найденное поле температуры (18) на временном слое k=1:
Рис. 4. Схема
узлов области решения в момент времени τ (k=1):
○ – координаты внутренних узлов; ● – координаты узлов в начальный момент времени; ● – координаты узлов в момент времени τ (k=1);
×, × – координаты граничных узлов левой и правой границ соответственно(18)
Слайд 16ПРОДОЛЖЕНИЕ
14
Составим СЛАУ для второго временного слоя 2τ (k=2) для
всех узлов i=0…Nx аналогичное выражению (14).
Выпишем значения коэффициентов ai, bi,
ci, di (i=0…Nx) входящих в СЛАУ (19) и сравним полученные коэффициенты с выражениями (15) – (17) для первого временного слоя k=1.(19)
Слайд 17ПРОДОЛЖЕНИЕ
15
На левой границе × (i=0) используя аппроксимированное граничное условие
(9):
Внутри области решения ○ (i=1…Nx – 1 ) используя коэффициенты
аппроксимированного уравнения теплопроводности (13) на втором временном слое 2τ (k=2): где значения температуры в момент времени τ (k=1) в узлах ● известны из решения СЛАУ (14), выражение (18):
На правой границе × (i=0) используя аппроксимированное граничное условие (10):
(20)
Слайд 18ПРОДОЛЖЕНИЕ
16
Сравнивая значения коэффициентов ai, bi, ci, di (i=0…Nx) входящих
в СЛАУ (14), формулы (15) – (17), со значениями коэффициентов
ai, bi, ci, di входящих в СЛАУ (19), обнаружим несоответствие только лишь в одном коэффициенте di (см. формулы (16) и (20)).Таким образом, следует при расчете температурного поля на новом временном Tik+1 , i=1…Nx–1 слое всякий раз обновлять значения коэффициента di i=1…Nx–1 используя известное поле температуры с предыдущего временного слоя Tik , i=1…Nx–1.
Отметим так же, что если теплофизические коэффициенты не зависят от температуры и граничные условия не зависят от времени, т.е. являются постоянными во все время процесса, то не имеет смысла вычислять повторно, например в цикле по времени.
(16)
(20)
Слайд 194. АЛГОРИТМ РЕШЕНИЯ
17
1. Задание входных данных (const): lamda, ro,
сp, Lx , Nx, Time, Nt, T0, TL,TR.
2. Определить
тип массива данных: type vec=array[0..Nx] of real.3. Описать используемые переменные в разделе var:
var ai, bi, ci, di, Ti : vec;
i, k : integer; txt : text;
hx, tau, t : real;
4. Задать процедуру решения СЛАУ
procedure TDMA(N:integer; a, b, c, d : vec; var x : vec);
var i : integer; z : real;
P, Q : vec;
Begin
P[0]:= – c[0]/b[0]; Q[0]:=d[0]/b[0];
for i:=1 to N do begin
z:=a[i]*P[i – 1]+b[i];
P[i]:= – c[i]/z;Q[i]:=(d[i] – a[i]*Q[i – 1])/z;
end;
x[N]:=Q[N];
for i:=N – 1 downto 0 do
x[i]:=P[i]*x[i+1]+Q[i];
End;
Слайд 20ПРОДОЛЖЕНИЕ
18
5. Начать основную программу с оператора: BEGIN clrscr;
6. Вычислить
шаги по пространству (hx) и времени (τ):
hx:=Nx; tau:=Nt;
hx:=Lx/hx; tau:=Time/tau;
7. Задать полю температуры
начальное условие:for i := 0 to Nx do
Ti[i] := T0;
8. Задать матрицу коэффициентов ai, bi, ci (i=0…Nx), d0 и dNx
{vi4esleie koefficientov SLAU}
ai[0]:=0.0; bi[0]:=1.0; ci[0]:=0.0; di[0]:=TL;
ai[Nx]:=0.0; bi[Nx]:=1.0; ci[Nx]:=0.0; di[Nx]:=TR;
z:=hx*hx;
for i:=1 to Nx-1 do begin
ai[i]:=-lamda/z;
bi[i]:=2.0*lamda/z+ro*cp/tau;
ci[i]:=-lamda/z;
end;
Слайд 21ПРОДОЛЖЕНИЕ
19
10. Произвести вычисление температуры в каждый момент времени до
тех пор пока значение времени t не станет равным Time:
z:=ro*cp/tau;t:=0;
WHILE (t
for i:=1 to Nx-1 do
di[i]:=z*Ti[i];
TDMA(Nx,ai,bi,ci,di,Ti);
End;
11. Вывести полученное поле температуры в файл:
Assign(txt,'T(x).txt');
Rewrite(txt);
for i:=0 to Nx do
writeln(txt,' ',hx*i:16:5,' ',Ti[i]:16:5);
close(txt);
12. Закончить основную программу оператором:
END.
Слайд 22ПРОДОЛЖЕНИЕ
20
Рис. 5. Распределение температуры
по толщине пластины в момент
времени t = 60 c
Результат решения задачи (2) – (5)
представлен на рис. 5.Слайд 23ЛИТЕРАТУРА
Кузнецов Г.В., Шеремет М.А. разностные методы решения задач теплопроводности:
учебное пособие. / Г.В. Кузнецов, М.А. Шеремет. — М.:Томск: Изд-во
ТПУ, 2007. — 172 с.Численные методы. Сборник задач: учеб. Пособие для вузов / В.Ю. Гидаспов, И.Э. Иванов, Д.Л. Ревизников и др.; под ред. У.Г. Пирумова. — М.: Дрофа, 2007. — 144 с.: ил. ISBN 978-5-358-01310-0
21