Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Маслов Евгений Анатольевич доц., к.ф.-м.н. Кафедра
Содержание
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Маслов Евгений Анатольевич доц., к.ф.-м.н. Кафедра
- 2. Слайд 2
- 3. СОДЕРЖАНИЕМЕТОД РАСЩЕПЛЕНИЯ МЕТОД ДРОБНЫХ ШАГОВПРИМЕР4. АЛГОРИТМ РЕШЕНИЯСПИСОК ЛИТЕРАТУРЫ2
- 4. 1. МЕТОД РАСЩЕПЛЕНИЯ ОБЩИЕ СВЕДЕНИЯ3 При численном
- 5. ПРОДОЛЖЕНИЕ Рассмотрим эти методы на примере задачи
- 6. ПРОДОЛЖЕНИЕ Введем пространственно-временную сетку с шагами hx,
- 7. 2. МЕТОД ДРОБНЫХ ШАГОВ (МДШ) 6(8)(9)С помощью чисто
- 8. ПРОДОЛЖЕНИЕ Схема МДШ имеет порядок сходимости O(τ+h2),
- 9. 3. ПРИМЕР Схема взаимодействия высокотемпературной струи с
- 10. ПРОДОЛЖЕНИЕ 9 При постановке задачи были приняты
- 11. ПРОДОЛЖЕНИЕ10 Граничные условия:– условие (II род) симметрии
- 12. ПЕРЕРЫВ
- 13. 4. АЛГОРИТМ РЕШЕНИЯ11 Для численного решения задачи
- 14. ПРОДОЛЖЕНИЕ12 Разностные уравнения типа (8), (9) сводятся
- 15. ПРОДОЛЖЕНИЕ13ai bi ci di i=0 0
- 16. ПРОДОЛЖЕНИЕ14 aj bj cjdj j=0 0
- 17. ПРОДОЛЖЕНИЕ15 Результаты вычисления при следующих значениях геометрических
- 18. ПРОДОЛЖЕНИЕ16 1. Задание входных данных (const): Nx=100;
- 19. 4. АЛГОРИТМ РЕШЕНИЯ17 4. Задать процедуру решения
- 20. ПРОДОЛЖЕНИЕ18 5. Начать основную программу с оператора:
- 21. ПРОДОЛЖЕНИЕ19 9. Произвести вычисление температуры МДШ в
- 22. ПРОДОЛЖЕНИЕ20 9b. Осуществить прогонку в направлении оси
- 23. ПРОДОЛЖЕНИЕ2110. Произвести экстраполяцию решения на угловые точки
- 24. ЛИТЕРАТУРА Кузнецов Г.В., Шеремет М.А. разностные методы
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Маслов Евгений Анатольевич
доц., к.ф.-м.н.
Кафедра атомных и тепловых электростанций
Корпус 4,
ауд 234
Слайд 41. МЕТОД РАСЩЕПЛЕНИЯ ОБЩИЕ СВЕДЕНИЯ
3
При численном решении многомерных задач
математической физики исключительно важным является вопрос об экономичности используемых методов.
Конечно-разностную
аппроксимацию называют экономичной, если число выполняемых операций (операций типа умножения) пропорционально числу узлов сетки.В настоящее время известно значительное количество экономичных разностных схем численного решения многомерных задач математической физики, основанных на расщеплении пространственных дифференциальных операторов по координатным направлениям и использовании метода скалярной прогонки (TDMA) вдоль этих направлений.
Из экономичных конечно-разностных схем, получивших наибольшее распространение, в данном разделе рассматриваются схемы методов переменных направлений и дробных шагов. Будем называть их общим термином – методы расщепления.
Слайд 5ПРОДОЛЖЕНИЕ
Рассмотрим эти методы на примере задачи для нестационарного двумерного
уравнения параболического типа (1) с постоянными коэффициентами в прямоугольнике со
сторонами Lx, Ly с соответствующими начальным (2) и граничными условиями первого рода (3) – (6).Для пространственно-временной области , , , рассмотрим следующую задачу:
4
(1)
(2)
(3)
(4)
(5)
(6)
Слайд 6ПРОДОЛЖЕНИЕ
Введем пространственно-временную сетку с шагами hx, hy, τ соответственно
по переменным x, y, t (см. рис. 1.):
и на этой
сетке будем аппроксимировать дифференциальную задачу (1) – (6) методом конечных разностей.Рис. 1. Схема пространственно-временной сетки
5
(7)
Слайд 72. МЕТОД ДРОБНЫХ ШАГОВ (МДШ)
6
(8)
(9)
С помощью чисто неявной подсхемы (8)
осуществляются скалярные прогонки в направлении оси x в количестве, равном
(Ny–1), в результате чего получается сеточная функция ui,jk+1/2. На втором дробном шаге по времени с помощью подсхемы (9) осуществляются скалярные прогонки в направлении оси y в количестве равном (Nx–1), в результате чего получается сеточная функция ui,jk+1. Шаблон схемы приведен на рис. 2.Рис. 2.
Слайд 8ПРОДОЛЖЕНИЕ
Схема МДШ имеет порядок сходимости O(τ+h2), т.е. первый порядок
по времени и второй – по переменным x и y.
В
литературе МДШ называют также методом покоординатного расщепления и локально-одномерным методом.К достоинствам схемы МДШ можно отнести простоту в алгоритмизации и программировании и абсолютную устойчивость с большим запасом устойчивости даже для задач, содержащих смешанные производные. В то же время недостатки МДШ следующие: на каждом дробном шаге достигается частичная аппроксимация (полная аппроксимация достигается на последнем дробном шаге, т.е. имеет место суммарная аппроксимация), схема имеет первый порядок точности по времени.
В качестве примера применения метода конечных разностей рассмотрим задачу на основе двумерного нестационарного уравнения теплопроводности. Анализируется задача теплообмена между высокотемпературной струей и пластиной из конструкционного материала (КМ), внешняя поверхность которого подвергается воздействию высокотемпературной высокоскоростной одно- или двухфазной струи с заданными параметрами.
7
Слайд 93. ПРИМЕР
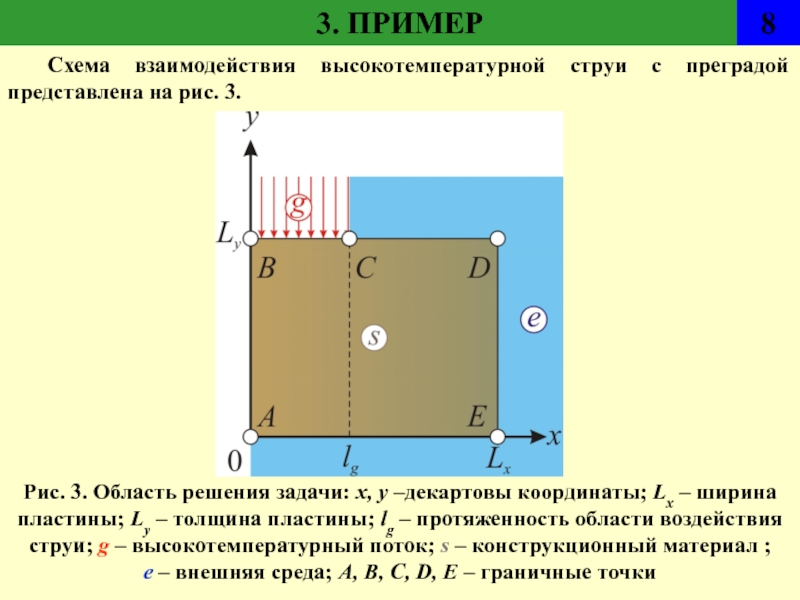
Схема взаимодействия высокотемпературной струи с преградой представлена на
рис. 3.
Рис. 3. Область решения задачи: x, y –декартовы координаты;
Lx – ширина пластины; Ly – толщина пластины; lg – протяженность области воздействия струи; g – высокотемпературный поток; s – конструкционный материал ; e – внешняя среда; A, B, C, D, E – граничные точки8
Слайд 10ПРОДОЛЖЕНИЕ
9
При постановке задачи были приняты следующие допущения:
1. Вклад
радиационной составляющей в теплообмен на внешней поверхности не учитывается.
2.
Возможные процессы плавления и окисления материала преграды активными компонентами газового потока не рассматриваются.3. Влияние конденсированной фазы в струе на теплообмен учитывается через коэффициент теплообмена αg на разрушающейся поверхности.
4. Теплофизические характеристики (λ, ρ, с) КМ постоянны.
Математическая модель, описывающая в рамках сформулированной задачи процесс прогрева КМ, включает нестационарное двумерное уравнение теплопроводности (10) с соответствующими начальным (11) и граничными условиями (12) – (16):
Начальное условие:
Ts(x, y) = T0 ≡ const.
(10)
(11)
Слайд 11ПРОДОЛЖЕНИЕ
10
Граничные условия:
– условие (II род) симметрии на оси 0y
(AB):
– условие (III род) кондуктивно-конвективного теплообмена газового потока с поверхностью
КМ (BC): – условие (III род) кондуктивно-конвективного теплообмена с воздухом на нагреваемой поверхности (CD):
– условие (III род) кондуктивно-конвективного теплообмена с воздухом на боковой поверхности (DE):
– условие (III род) кондуктивно-конвективного теплообмена с воздухом на тыльной стороне пластины (AE):
где T – температура; t – время; ρ – плотность; с – коэффициент удельной теплоемкости; λ – коэффициент теплопроводности; α – коэффициент теплообмена. Индексы "g", "e" и "s" относятся к характеристикам струи, окружающей среды и материала пластины соответственно.
(12)
(13)
(14)
(15)
(16)
Слайд 134. АЛГОРИТМ РЕШЕНИЯ
11
Для численного решения задачи (10) – (16)
воспользуемся МДШ. Для аппроксимации дифференциального уравнения (10) разностным методом введем
пространственно–временную сетку (7). Таким образом, вся расчетная область покрывается сеткой (рис. 1, 2). Введем следующее обозначение: T(xi,yj,tk)=Ti,jk. Дискретизацию уравнения (10) будем проводить в разностном виде, используя неявную схему на каждом полушаге по времени см. (8), (9). Аппроксимируем начальное (11) и граничные условия (12) – (16):(17)
(18)
(19)
(20)
(21)
(22)
Слайд 14ПРОДОЛЖЕНИЕ
12
Разностные уравнения типа (8), (9) сводятся к стандартному трехдиагональному
виду (23) и (24) соответственно и решаются последовательно методом прогонки
(TDMA):Выпишем коэффициенты СЛАУ вида (23) в направлении оси х с учетом (8), (18) и (21) и СЛАУ вида (24) в направлении оси y с учетом (9), (19), (20), (22).
(23)
(24)
Слайд 15ПРОДОЛЖЕНИЕ
13
ai
bi
ci
di
i=0
0
1
–λs/hx2
–λs/hx2
ρ∙cp/τ+2∙λs/hx2
Ti,jk∙ρ∙cp/τ
Te∙αe∙hx/λs
1+Te∙αe∙hx/λs
–1
0
Слайд 16ПРОДОЛЖЕНИЕ
14
aj
bj
cj
dj
j=0
0
–λs/hy2
–λs/hy2
ρ∙cp/τ+2∙λs/hy2
Ti,jk+1/2∙ρ∙cp/τ
Te∙αe∙hy/λs
1+Te∙αe∙hy/λs
–1
0
0
1+Te∙αe∙hy/λs
Te∙αe∙hy/λs
1+Tg∙αg∙hy/λs
–1
0
Tg∙αg∙hy/λs
Слайд 17ПРОДОЛЖЕНИЕ
15
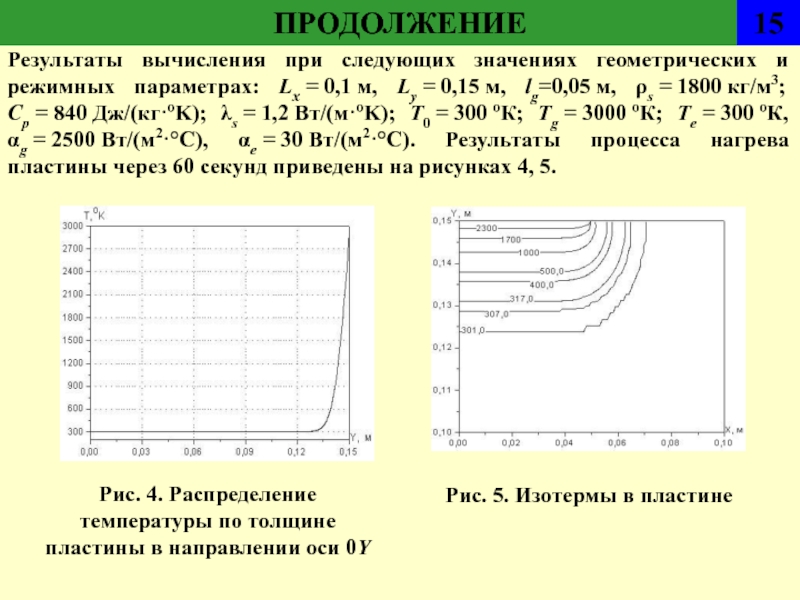
Результаты вычисления при следующих значениях геометрических и режимных параметрах:
Lx = 0,1 м, Ly = 0,15 м, lg=0,05 м, ρs = 1800 кг/м3; Ср = 840 Дж/(кг·ºK); λs = 1,2 Вт/(м·ºK); T0 = 300 ºК; Tg = 3000 ºК; Te = 300 ºК, αg = 2500 Вт/(м2·°С),
αe = 30 Вт/(м2·°С). Результаты процесса нагрева пластины через 60 секунд приведены на рисунках 4, 5.Рис. 5. Изотермы в пластине
Слайд 18ПРОДОЛЖЕНИЕ
16
1. Задание входных данных (const):
Nx=100; Ny=50; Nt=60; {размерность сетки}
Lx=0.1;
Ly=0.15; Time_end=60.; lg=0.05;{геометрически харк-ки}
Lamda=1.2; Ro=1800.; сp=840.; {теплофизические хар-ки}
T0=300.; Te=300.; alfae=30.;
alfag=2500.;{физические хар-ки}2. Определить тип динамического массива данных:
type arr=array of real;
3. Описать используемые переменные в разделе var:
var a, b, c, d, T : arr; {динамические массивы}
i, j, k,Nxlg : integer;
txt : text;
z, hx, hy, ht : real;
Tij : array [0..Nx, 0..Ny] of real;
Слайд 194. АЛГОРИТМ РЕШЕНИЯ
17
4. Задать процедуру решения СЛАУ с использованием
динамических массивов
procedure TDMA(N : integer; var a, b, c, d,
x : arr);var i : integer; z : real;
P, Q : arr;
Begin
Setlength (P, N+1); Setlength (Q, N+1);
P[0]:= – c[0]/b[0]; Q[0]:=d[0]/b[0];
for i:=1 to N do begin
z:=a[i]*P[i – 1]+b[i];
P[i]:= – c[i]/z;Q[i]:=(d[i] – a[i]*Q[i – 1])/z;
end;
x[N]:=Q[N];
for i:=N – 1 downto 0 do
x[i]:=P[i]*x[i+1]+Q[i];
End;
Слайд 20ПРОДОЛЖЕНИЕ
18
5. Начать основную программу с оператора: BEGIN clrscr;
6. Вычислить
шаги по пространству (hx, hy) и времени (τ):
hx:=Nx; hy :=Ny ; ht:=Nt;
hx:=Lx/hx; hy :=Ly/hy; ht:=Time_end/ht;
7. Определить колическтво
узлов воздействия струи:Nxlg:=trunk(lg/hx);
8. Задать начальное поле
температуры (начальное условие):
for i := 0 to Nx do
for j := 0 to Ny do
Tij[i, j] := T0;
Слайд 21ПРОДОЛЖЕНИЕ
19
9. Произвести вычисление температуры МДШ в каждый момент времени
до тех пор пока значение времени Time не станет равным
Time_end:Time:=0;
WHILE Time
9a. Осуществить прогонку в направлении оси х
Setlength(a, Nx+1); Setlength(b, Nx+1); Setlength(c, Nx+1);
Setlength(d, Nx+1); Setlength(T, Nx+1);
a[0] := 0.; a[Nx] := –1.;
b[0] := –1.; b[Nx] := 1.+Te*Alfae*hx/Lamda;
c[0] := 1.; c[Nx] := 0.;
d[0] := 0.; d[Nx] := Te*Alfae*hx/Lamda;
For j := 1 to Ny–1 do Begin
for i:=1 to Nx–1 do begin
a[i] := –Lamda/hx/hx; c[i]:=a[i];
b[i] : = Ro*cp/ht+2.*Lamda/hx/hx; d[i] := Tij[i,j]*Ro*cp/ht;
end;
TDMA(Nx, a, b, c, d, T);
for i := 0 to Nx do Tij[i,j] := T[i];
End;
Слайд 22ПРОДОЛЖЕНИЕ
20
9b. Осуществить прогонку в направлении оси y
Setlength(a, Ny+1); Setlength(b, Ny+1); Setlength(c, Ny+1);
Setlength(d, Ny+1); Setlength(T, Ny+1); a[0] := 0.; a[Ny] := –1..;
b[0] := –1.; b[Ny] := 1.+Tg*Alfag*hy/Lamda;
c[0] := 1.; c[Ny] := 0.;
d[0] := 0.; d[Ny] := Tg*Alfag*hy/Lamda;
For i := 1 to Nx–1 do Begin
if i = Nxlg+1 then begin
a[Ny] := –1..; b[Ny] := 1.+Te*Alfae*hy/Lamda;
c[Ny] := 0.; d[Ny] := Te*Alfae*hy/Lamda;
end;
for j: = 1 to Nx–1 do begin
a[j] := –Lamda/hy/hy; c[j]:=a[j];
b[j] : = Ro*cp/ht+2.*Lamda/hy/hy; d[j] := Tij[i,j]*Ro*cp/ht;
end;
TDMA(Ny, a, b, c, d, T);
for j := 0 to Ny do Tij[i,j] := T[j];
End;
END;
Слайд 23ПРОДОЛЖЕНИЕ
21
10. Произвести экстраполяцию решения на угловые точки
Tij[0,Ny] :=
Tij[1,Ny]; Tij[Nx,Ny] := Tij[Nx–1,Ny];
Tij[0,0] := Tij[1,0]; Tij[Nx,0] :=
Tij[Nx–1,0];11. Вывести полученное поле температуры в файл:
Assign(txt,'T(x,y).txt');
Rewrite(txt);
for i:=0 to Nx do
for j:=0 to Ny do
writeln(txt,' ',hx*i:16:5,' ',hy*j:16:5,
' ',Tij[i,j]:16:5);
close(txt);
12. Закончить основную
программу оператором:
END.
Слайд 24ЛИТЕРАТУРА
Кузнецов Г.В., Шеремет М.А. разностные методы решения задач теплопроводности:
учебное пособие. / Г.В. Кузнецов, М.А. Шеремет. — М.:Томск: Изд-во
ТПУ, 2007. — 172 с.Численные методы. Сборник задач: учеб. Пособие для вузов / В.Ю. Гидаспов, И.Э. Иванов, Д.Л. Ревизников и др.; под ред. У.Г. Пирумова. — М.: Дрофа, 2007. — 144 с.: ил. ISBN 978-5-358-01310-0
22




















![МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Маслов Евгений Анатольевич
доц., к.ф.-м.н.
Кафедра ПРОДОЛЖЕНИЕ2110. Произвести экстраполяцию решения на угловые точки Tij[0,Ny] := Tij[1,Ny]; Tij[Nx,Ny] ПРОДОЛЖЕНИЕ2110. Произвести экстраполяцию решения на угловые точки Tij[0,Ny] := Tij[1,Ny]; Tij[Nx,Ny] := Tij[Nx–1,Ny]; Tij[0,0] :=](/img/thumbs/ba44a865e03d060fad38f2e133865a0c-800x.jpg)