Математическое описание случайных явлений 1 22.01.2019

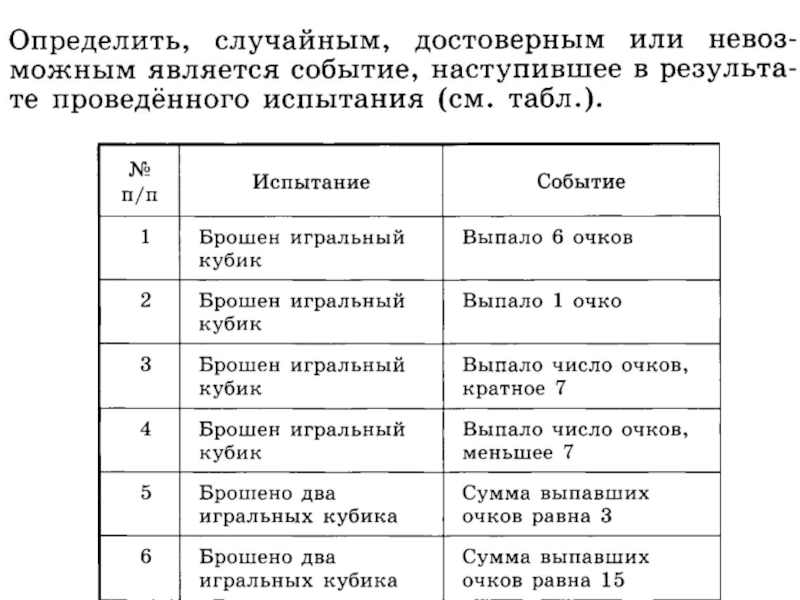
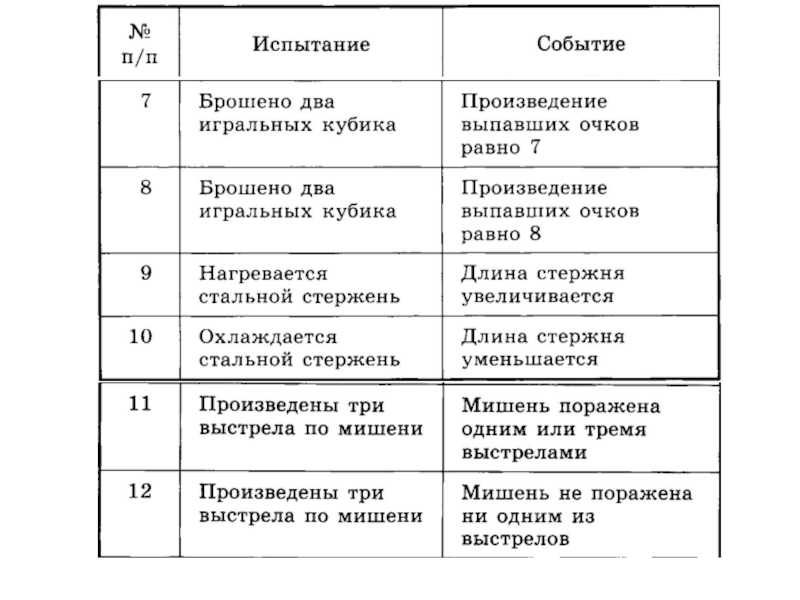
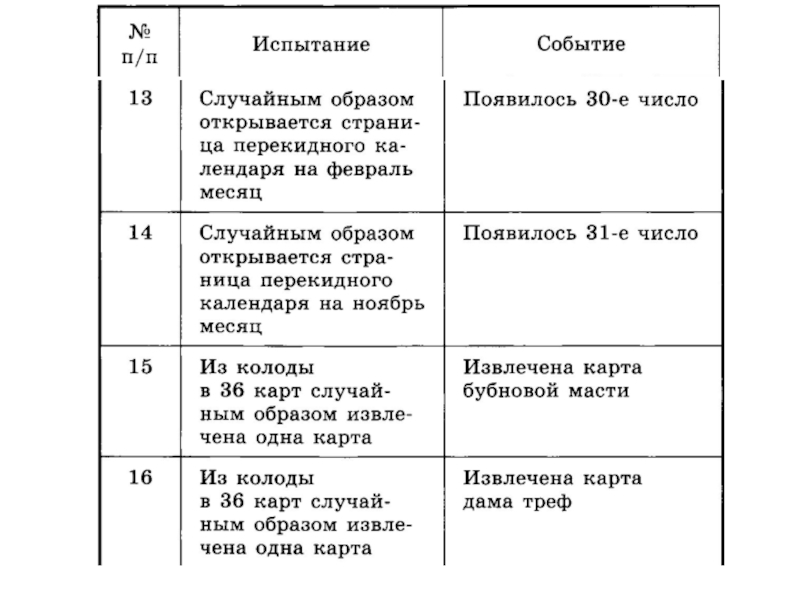
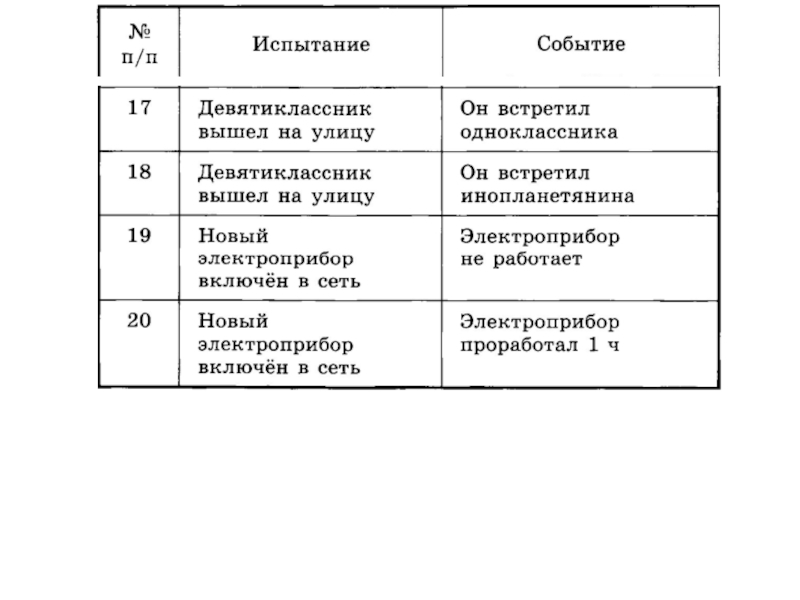
данных обстоятельствах непременно произойдет.
А={в следующем году первый снег в Питере

В={свалившийся со стола бутерброд упадет на пол маслом вниз};

С={ при бросании кубика выпадет шестерка};

D= {npu бросании кубика выпадет нечетное число очков}.

2

могут.
F={ npu бросании кубика выпадет девять}.
Достоверное событие - это событие,

Н={при бросании кубика выпадет число очков, меньшее 10}

3

одновременно.
Несовместные события НЕ могут происходить в данных условиях одновременно.
8

«наступил вечер».
6

которых может осуществиться случайное событие, принято называть случайным опытом, или

4

элементарными событиями.

5

два очка», «выпало три очка», «выпало четыре очка», «выпало пять

6

Элементарным событием при двух бросаниях игральной кости является пара чисел.

6

которых одинаковы.

8

При бросании двух игральных костей равновозможных элементарных
событий 36.




Вопросы:
1.Равновозможны ли

9

шестерку из перетасованной колоды карт}?
Шестерок на кубике - 1
Всего граней

1 шанс из 6

Шестерок в колоде - 4

Всего карт в колоде - 36

4 шанса из 36

10

называть ВЕРОЯТНОСТЬЮ этого события и обозначать буквой P (от латинского

10

Ученые наблюдали за игрой в кости и делали математические выводы…

равновозможных элементарных событий случайного опыта.



11

события, если их общее число равно 17.
Решение:
b – элементарное событие

12

случайный эксперимент, в котором три элементарных события: a, b, c.

13

случайный эксперимент, в котором бросают шестигранный кубик.
Определить элементарные события. Найти

13

элементарными событиями, благоприятствующими событию А.


14

события:
«выпало 2 очка»,
«выпало 4 очка»,
«выпало шесть очков».
15

очередь. Все возможные события в этом случае складываются из элементарных

Ему благоприятствуют элементарные события:
«ЮАН»,
«ЮНА».

Рассмотрим событие : «Ю стоит первой».

16

очередь. Все возможные события в этом случае складываются из элементарных

Ему благоприятствуют элементарные события:
«НЮА», «НАЮ», «ЮНА».

Рассмотрим событие : «Н стоит впереди А».

17

: «сумма очков при двух бросках равна 11».
Ему благоприятствуют элементарные

18

: «произведение очков при двух бросках равна 12».
Ему благоприятствуют элементарные

19

события называются достоверными;
с) для случайных событий: 0 < Р(А) < 1.
20

о каких мы можем сказать, что оно «маловероятно» или «очень

21

событию.


P(A)=P(a)+P(b)+P(с)+P(d),
где А-событие,
а, b, c, d – элементарные события, благоприятствующие

22

города Васюки, вероятность выигрыша Остапа равна 0,001, вероятность ничьей равна

Решение:
Благоприятствующие события:
«Остап выиграл»,
«партия окончилась вничью».

P(A) = 0,001 + 0,01 = 0,011

23

равна 0,5, вероятность элементарного события «автомобиль свернет влево» равна 0,3,

Решение:
Благоприятствующие события:
«автомобиль свернет вправо»,
«автомобиль свернет влево»,
«автомобиль поедет прямо».

P(A) = 0,5 + 0,3 + 0,18 = 0,98

24

попадания в зоны мишени представлены в таблице:

Найдите вероятность события:
а) «стрелок

26

событие,
N- число равновозможных элементарных событий случайного опыта.
27

событию, к общему числу элементарных событий.

Р(А)=N(A)/ N