Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механические свойства твердых тел. Механические колебания. Звук и
Содержание
- 1. Механические свойства твердых тел. Механические колебания. Звук и
- 2. Основная литература для подготовки:А.Н. Ремизов. Медицинская и
- 3. План лекции: Основные понятия, описывающие
- 4. Области применения биоматериалов Стоматологические восстановительные материалы,
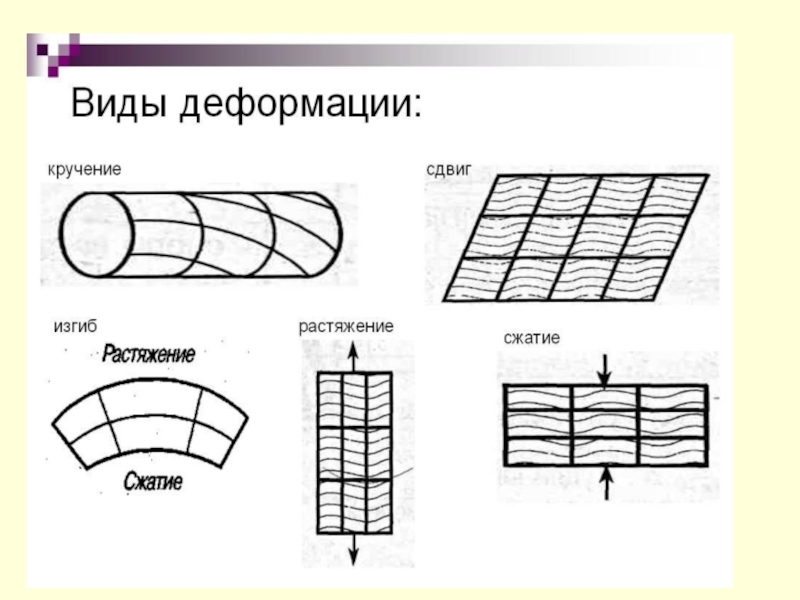
- 5. Механические свойства твердых тел.1.Определение : Твердым телом
- 6. Слайд 6
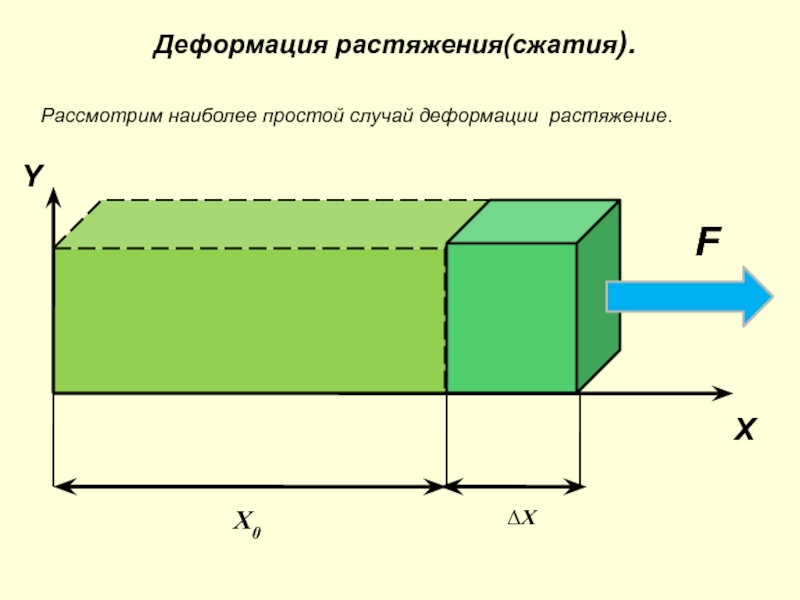
- 7. Деформация растяжения(сжатия).Рассмотрим наиболее простой случай деформации растяжение.XYX0∆XF
- 8. - относительное удлинение - механическое напряжение(1.1)(1.2)Рассмотрим
- 9. Преобразуем данное выражение , умножим и разделим
- 10. Деформация сдвига.Предположим, что на тело действует сила
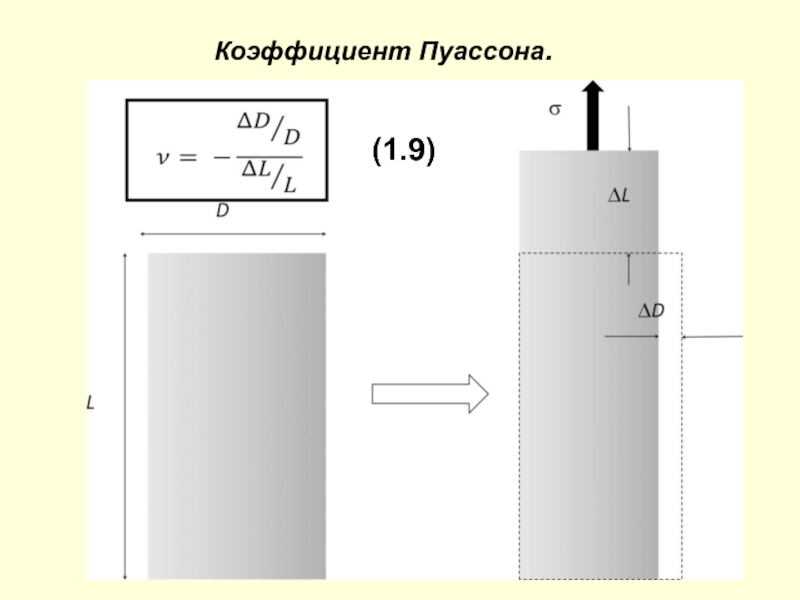
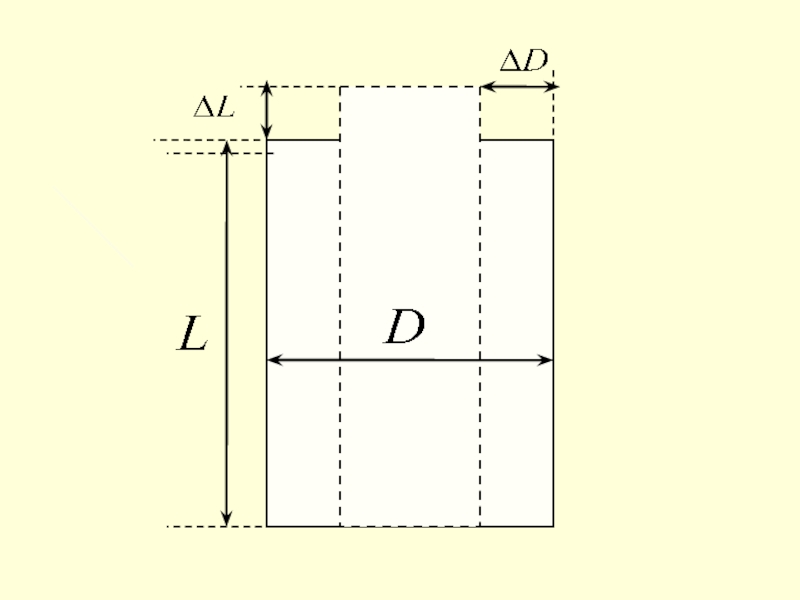
- 11. Коэффициент Пуассона.(1.9)
- 12. Слайд 12
- 13. Связь коэффициента Пуассонас другими коэффициентами. Коэффициент Пуассона
- 14. Зависимость напряжения в материале от удлинения (сжатия).
- 15. Если расстояние между молекулами невелико, то данную
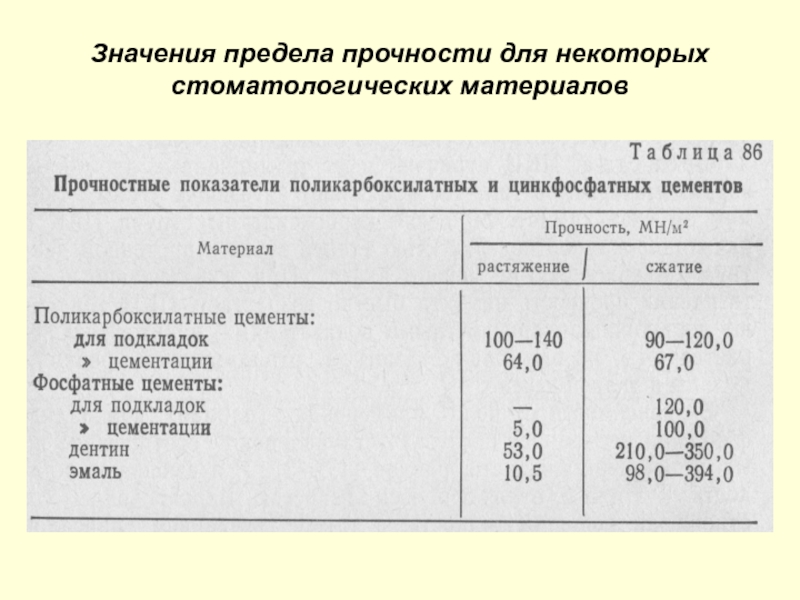
- 16. Значения предела прочности для некоторых стоматологических материалов
- 17. Моделирование механических свойств вязкоупругих материалов.Кость является композитным
- 18. (1.13)η – вязкость материалаσ - механическое напряжениеε - деформацияМодель Максвелла. (1.14)(1.15)
- 19. Скорость вязкой деформации выразим из (1.13)(1.16)Суммируя скорость
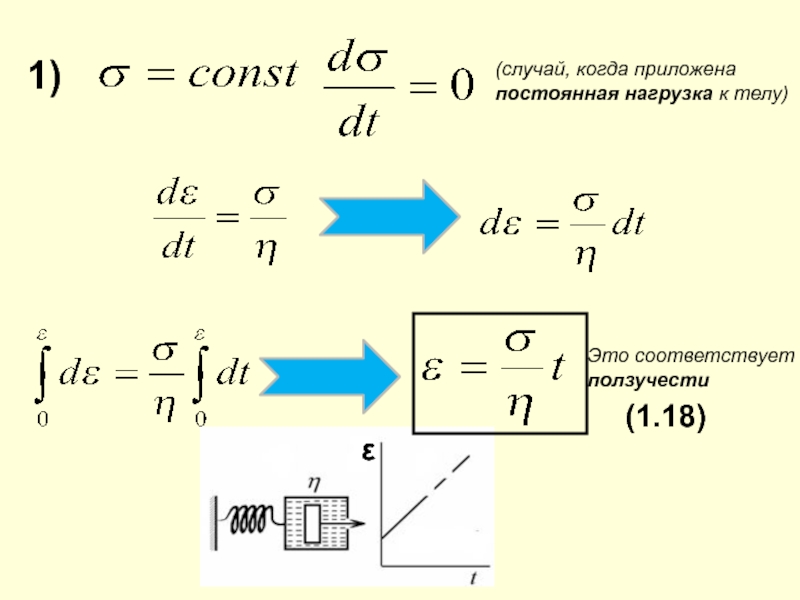
- 20. 1) Это соответствуетползучести ε(1.18)(случай, когда приложена постоянная нагрузка к телу)
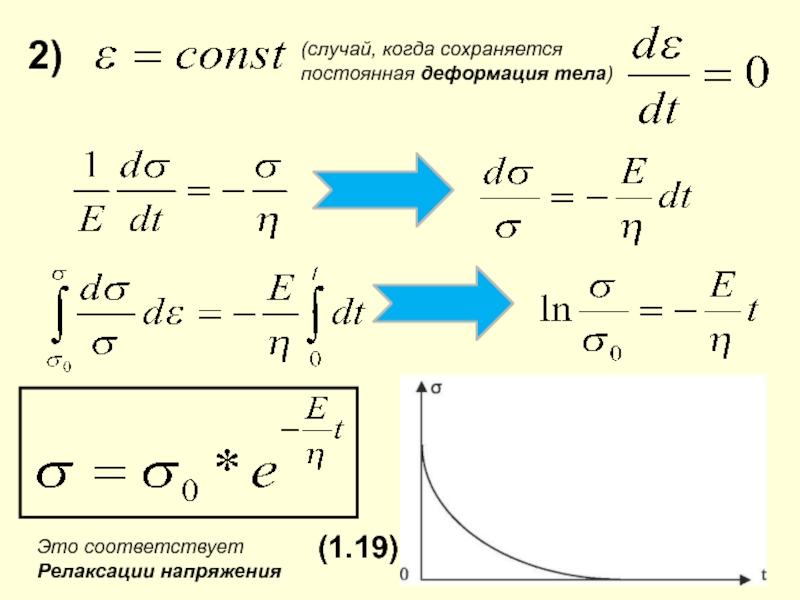
- 21. 2) Это соответствуетРелаксации напряжения (1.19)(случай, когда сохраняется постоянная деформация тела)
- 22. Модель Кельвина - Фойхта. Если мгновенно создать
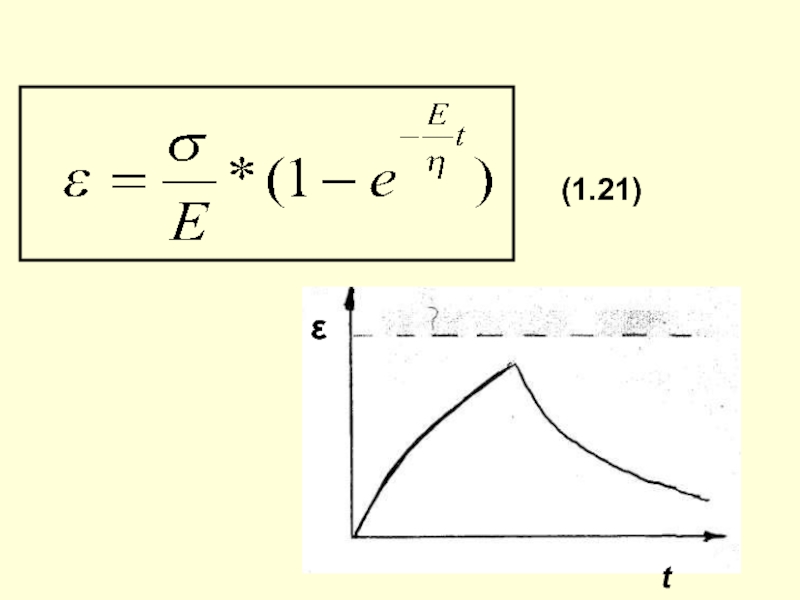
- 23. (1.21)εt
- 24. Механические свойства биологических тканейКостная тканьКость - основной
- 25. Строение трубчатойкости:1 – накостница2 – компактное вещ-во
- 26. Механические свойства кости и некоторых материалов.
- 27. Звуковые волны. Физические характеристики звука. 4.
- 28. Механические колебания. Свободные колебанияОпределение: Свободными колебаниями
- 29. Механические
- 30. ОХ1. Зададим колебание точки с координатой х
- 31. Аргумент при косинусе - фаза волныМножество
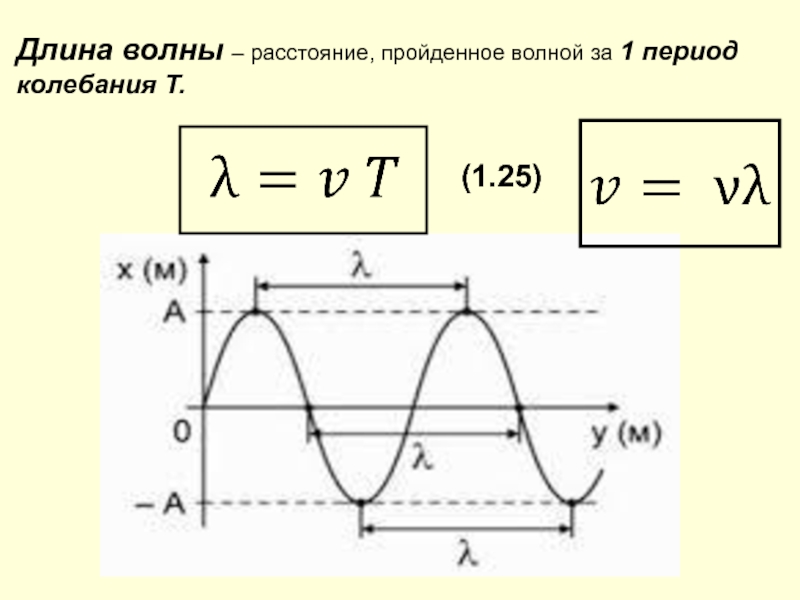
- 32. Длина волны – расстояние, пройденное волной за 1 период колебания T.(1.25)
- 33. Звуковые волны. Скорость звука. Звуковые колебания и
- 34. Слайд 34
- 35. Физические характеристики звука. Скорость звукаДлина волны звука Частота звукаИнтенсивность звуковой волны
- 36. Поток
- 37. Поток энергии волн, отнесенный к площади поверхности,
- 38. Удельный акустический импеданс. с – скорость
- 39. Таблица плотностей, скоростей звука и импеданса для
- 40. Пусть звуковая волна нормально падает к
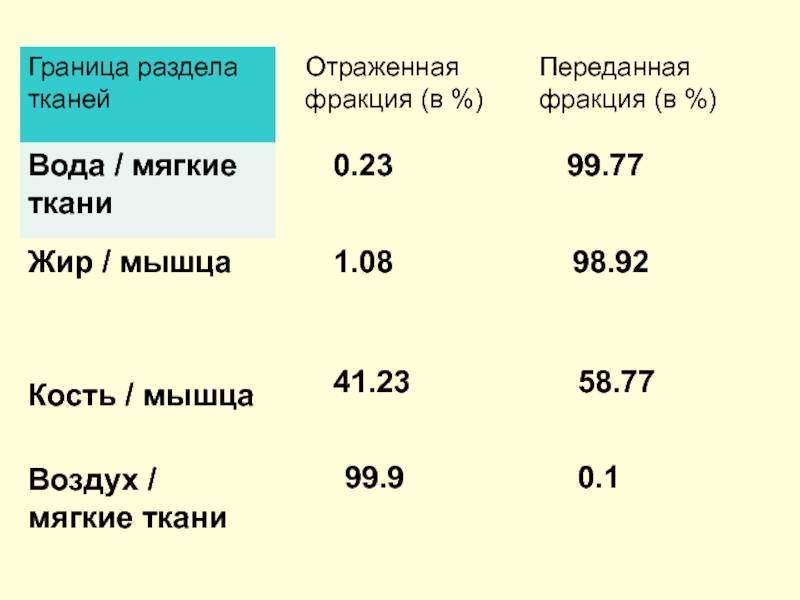
- 41. Максимальное значение, которое может принимать β равноИз
- 42. Слайд 42
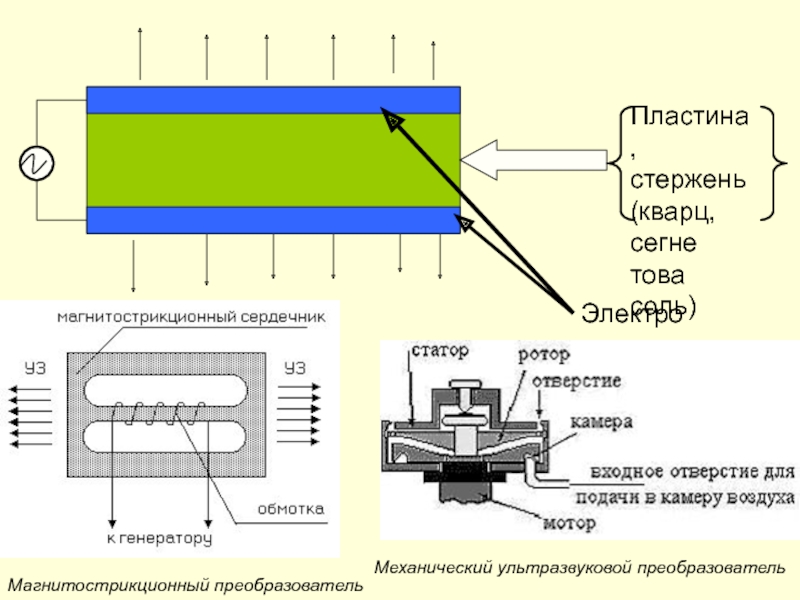
- 43. Определение: Ультразвуком называют механические колебания и волны,
- 44. Пластина,стержень(кварц, сегнетова соль)ЭлектродыМеханический ультразвуковой преобразовательМагнитострикционный преобразователь
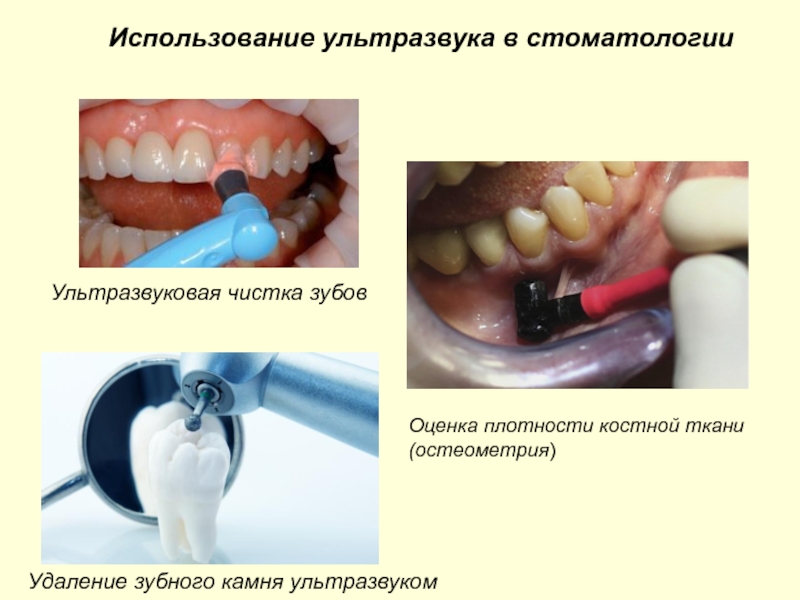
- 45. Ультразвуковая чистка зубовУдаление зубного камня ультразвукомИспользование ультразвука в стоматологииОценка плотности костной ткани (остеометрия)
- 46. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Основная литература для подготовки:
А.Н. Ремизов. Медицинская и биологическая физика: Учеб.
для вузов / А.Н. Ремизов. А.Г. Максина. А.Я.Потапенко. М.: Дрофа
2003-2014.Ремизов А.Н., Максина А.Г. Сборник задач по медицинской и биологической физике. 3-е изд., перераб. и дополн. –М.:Дрофа, 2008. –192 с.
Антонов В.Ф., Коржуев А.В. Физика и биофизика. Курс лекций для студентов мед. вузов. – М.: ГОЭТАР-Медиа, 2004.
Антонов В.Ф., Черныш А.М., Козлова Е.К., Коржуев А.В. Физика и биофизика. Учебник для студентов мед. вузов. – М.: ГОЭТАР-Медиа, 2008.
Антонов В.Ф., Черныш А.М., Пасечник В.И., Вознесенский С.А., Козлова Е.К. Биофизика. Учебник для студентов мед. вузов. – М.: Владос, 2003-288 с.
Дополнительная литература для подготовки:
Антонов В.Ф. Физика и биофизика. Практикум: учебное пособие для студентов мед. и фарм. вузов / Антонов В.Ф., Черныш А.М., Козлова Е.К., Коржуев А.В. – М.: ГЭОТАР-Медиа, 2008.
Лещенко В. Г. Медицинская и биологическая физика: учеб. пособие / В.Г.Лещенко,
Г.К. Ильич.- Минск : Новое знание ; М.: ИНФРА - М, 2014.-552 с.
Слайд 3План лекции:
Основные понятия, описывающие
механические свойства
и
характеристики твердых тел.
2. Моделирование механических свойств
вязкоупругих материалов.3. Механические свойства костной ткани.
4. Звуковые волны. Физические
характеристики звука.
Слайд 4Области применения биоматериалов
Стоматологические восстановительные материалы,
к которым
относятся металлические и композитные
пломбировочные материалы, а
также керамика для несъемного протезирования и материалы для съемных
зубных протезов.
Имплантаты, например внутричелюстные, имплантаты
челюстно – лицевых суставов.
Сердечно – сосудистые имплантаты, такие как протезы
клапанов сердца и сосудов.
Слайд 5Механические свойства твердых тел.
1.
Определение :
Твердым телом в механике называют
неизменяемую систему
материальных точек, при любых движениях которой взаимные расстояния
между
точками системы остаются неизменными. Определение :
Деформацией твердого тела называют изменение формы или
объема тела.
Определение :
Деформацию, исчезающую после прекращения действия приложенных сил называют Упругой. Пластическими или остаточными деформациями называют такие деформации, которые сохраняются в теле по крайней мере частично, после прекращения действия внешних приложенных сил.
Слайд 7Деформация растяжения(сжатия).
Рассмотрим наиболее простой случай деформации растяжение.
X
Y
X0
∆X
F
Слайд 8 - относительное
удлинение
- механическое
напряжение
(1.1)
(1.2)
Рассмотрим случай, когда деформация
является малой, т. е. мало :
∆X
- закон Гука
k – коэффициент жесткости
∆ - удлинение тела
(1.3)
F – сила, приложенная к телу
S – площадь поперечного сечения тела
Слайд 9Преобразуем данное выражение , умножим и разделим на x0
:
E
ε
- закон Гука
E – модуль Юнга
є – относительное
удлинение (сжатие)
(1.4)
Слайд 10Деформация сдвига.
Предположим, что на тело действует сила по касательной:
G – модуль сдвига, θ – угол сдвига
(1.5)
Для
малых деформаций θ ≈ 0, тогда: (1.6)
(1.7)
(1.8)
Слайд 13Связь коэффициента Пуассона
с другими коэффициентами.
Коэффициент Пуассона зависит только от
свойств
материала, из которого изготовлен образец, и
связан с относительным изменением объема V образца при
деформации :
2. Коэффициент Пуассона связан с модулем сдвига G
деформации сдвига:
(1.10)
(1.11)
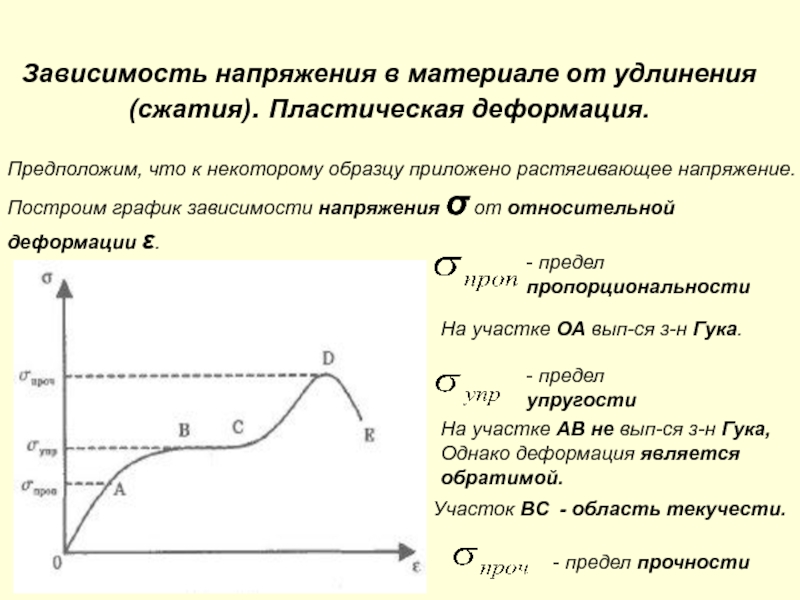
Слайд 14Зависимость напряжения в материале от удлинения (сжатия). Пластическая деформация.
Предположим, что
к некоторому образцу приложено растягивающее напряжение.
Построим график зависимости напряжения σ
от относительной деформации ε.
На участке ОА вып-ся з-н Гука.
- предел
пропорциональности
- предел
упругости
На участке АB не вып-ся з-н Гука,
Однако деформация является
обратимой.
Участок BС - область текучести.
- предел прочности
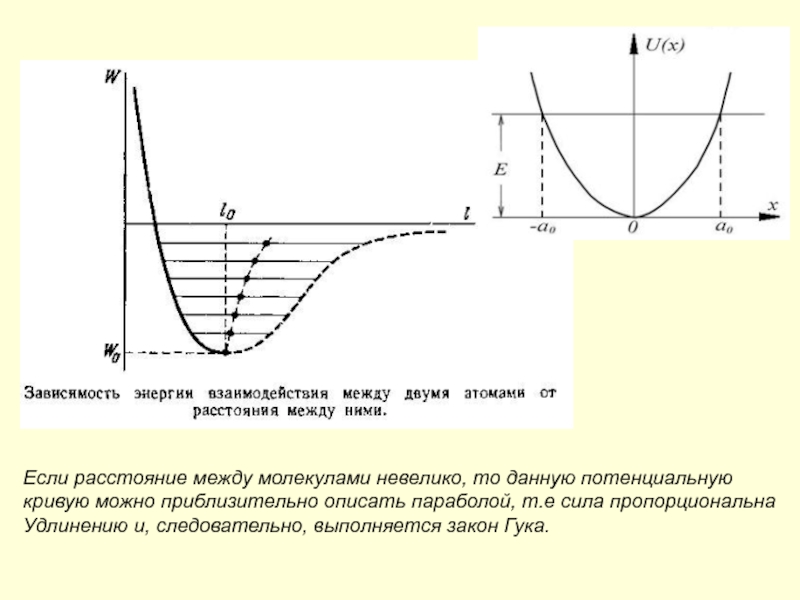
Слайд 15Если расстояние между молекулами невелико, то данную потенциальную
кривую можно
приблизительно описать параболой, т.е сила пропорциональна
Удлинению и, следовательно, выполняется закон
Гука. Слайд 17Моделирование механических свойств вязкоупругих материалов.
Кость является композитным материалом, состоящим из
неорганического материала и коллагена. Деформацию таких материалов часто называют вязкоупругой.
Модель упругих свойств – пружина
Модель вязких свойств - движение поршня
Будем считать, что деформацию упругой части материала можно описать
законом Гука.
Движение поршня можно описать следующим уравнением :
(1.12)
2.
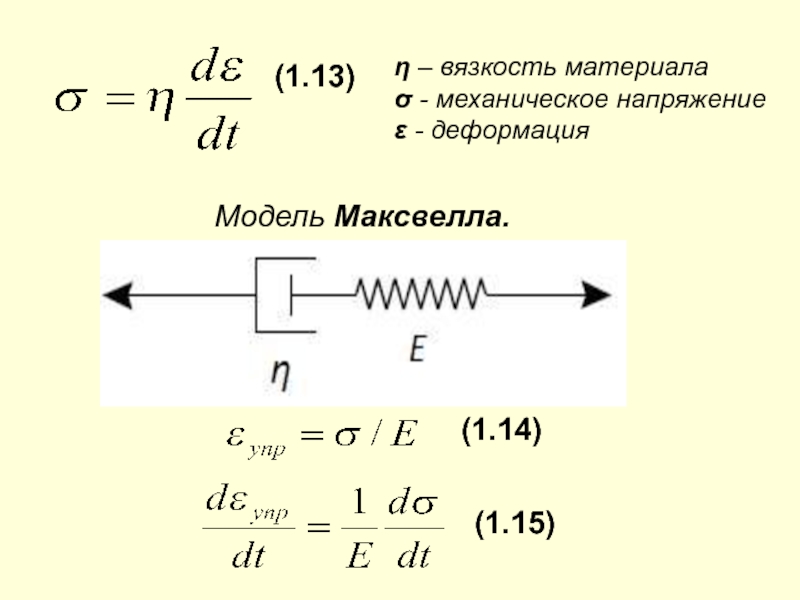
Слайд 18(1.13)
η – вязкость материала
σ - механическое напряжение
ε - деформация
Модель Максвелла.
(1.14)
(1.15)
Слайд 19Скорость вязкой деформации выразим из (1.13)
(1.16)
Суммируя скорость при упругой и
вязкой деформаций (1.15) и (1.16 ) найдем :
(1.17)
Возможны следующие два
предельных случая : Слайд 212)
Это соответствует
Релаксации напряжения
(1.19)
(случай, когда сохраняется
постоянная деформация тела)
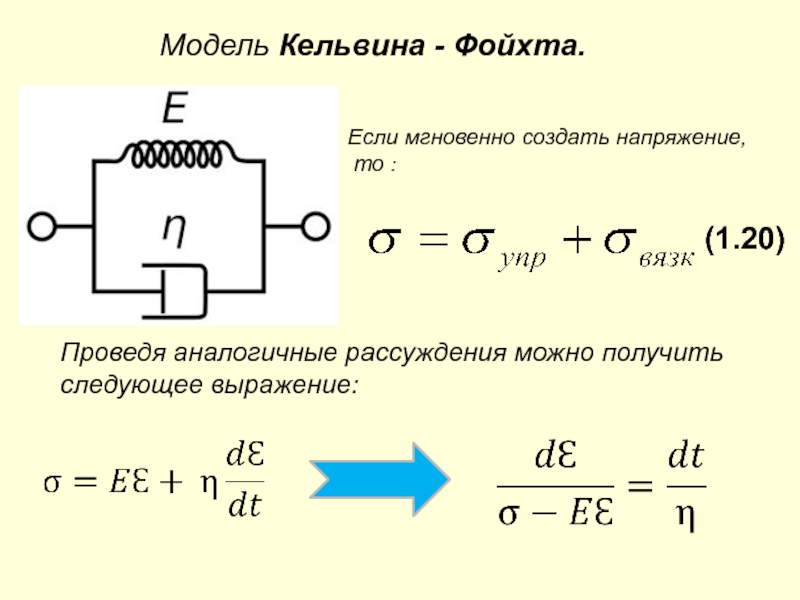
Слайд 22Модель Кельвина - Фойхта.
Если мгновенно создать напряжение,
то :
Проведя аналогичные рассуждения можно получить
следующее выражение:
(1.20)
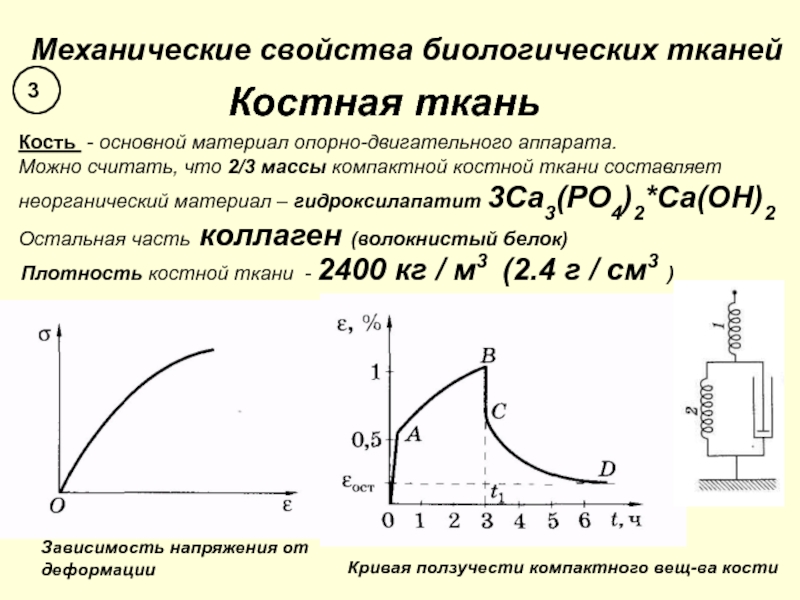
Слайд 24Механические свойства биологических тканей
Костная ткань
Кость - основной материал опорно-двигательного аппарата.
Можно
считать, что 2/3 массы компактной костной ткани составляет
неорганический материал –
гидроксилапатит 3Ca3(PO4)2*Ca(OH)2 Остальная часть коллаген (волокнистый белок)
Плотность костной ткани - 2400 кг / м3 (2.4 г / см3 )
Зависимость напряжения от
деформации
Кривая ползучести компактного вещ-ва кости
3
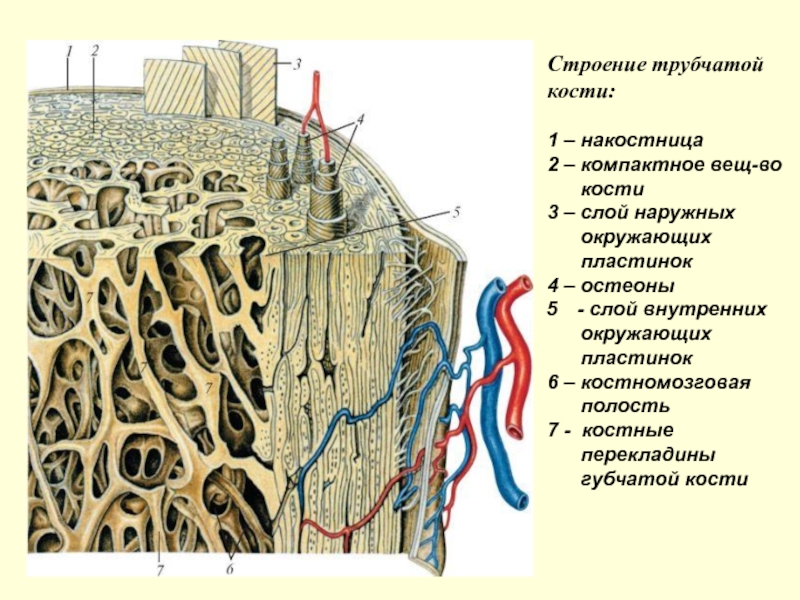
Слайд 25Строение трубчатой
кости:
1 – накостница
2 – компактное вещ-во
кости
3
– слой наружных
окружающих
пластинок4 – остеоны
- слой внутренних
окружающих
пластинок
6 – костномозговая
полость
7 - костные
перекладины
губчатой кости
Слайд 28Механические колебания.
Свободные колебания
Определение: Свободными колебаниями называют колебания,
которые
совершаются без внешних воздействий за счет
первоначально полученной телом энергии.
Примеры: пружинный маятник, математический маятник.
Звуковые волны
Ультразвуковые волны в
стоматологии
Ультразвуковые
волны в
косметологии
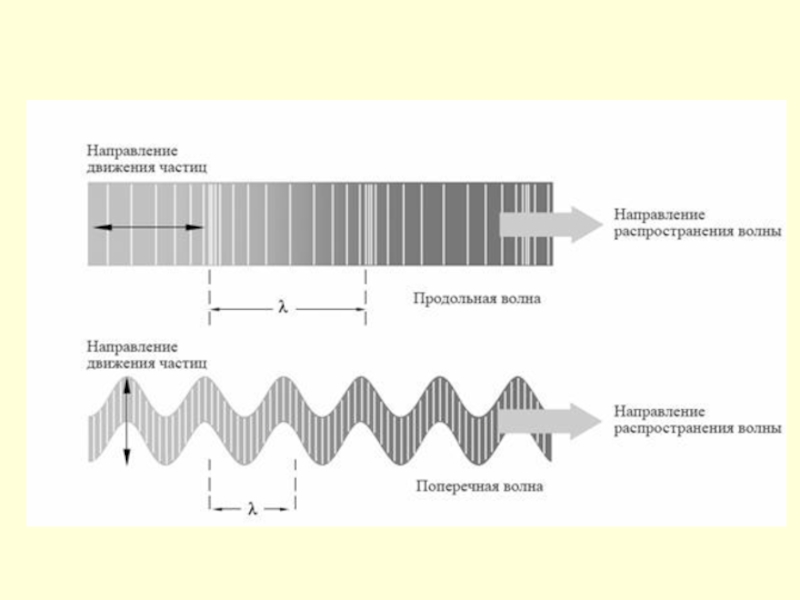
Слайд 29 Механические волны.
Уравнение механической волны.
Механической
волной называют механические возмущения, распространяющиеся в пространстве и несущие энергию.
Рассмотрим
механическую волну, распространяющуюся вдоль оси ОХ,зависимость записывается в общем виде:
S = f (x, t) (1.22)
S – зависимость смещения колеблющейся точки
x - расстояние
t - время
Возможны два случая :
1 – S и x – направлены по одной прямой ( продольные волны )
2 - S x ( поперечные волны )
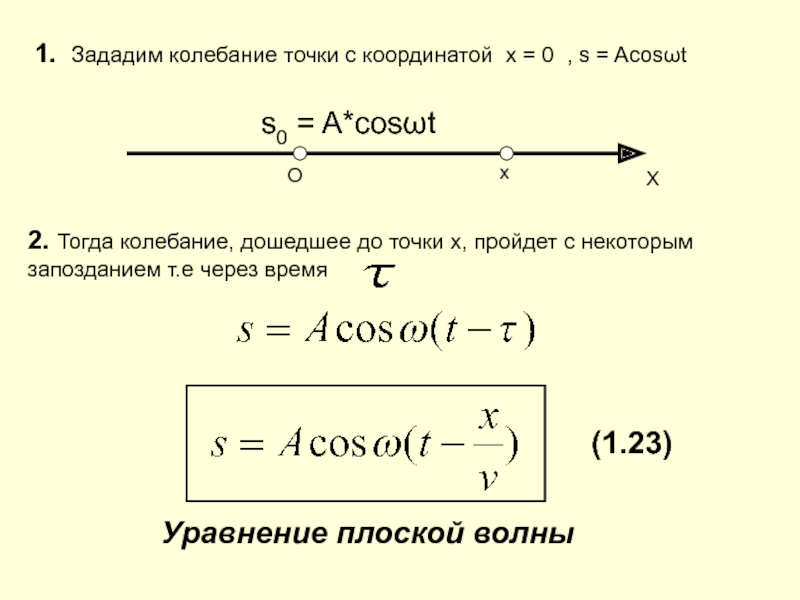
Слайд 30О
Х
1. Зададим колебание точки с координатой х = 0 ,
s = Acosωt
s0 = A*cosωt
2. Тогда колебание, дошедшее до
точки x, пройдет с некоторым запозданием т.е через время
х
(1.23)
Уравнение плоской волны
Слайд 31Аргумент при косинусе
- фаза волны
Множество точек, имеющих одинаковую
фазу – называют фронтом волны
х
x = const
Cкорость распространения фазы
называют фазовой скоростью (1.24)
Слайд 33Звуковые волны. Скорость звука.
Звуковые колебания и волны – это
частный случай
механических колебаний и волн.
Звук – продольные механические
волны.E – Модуль Юнга
ρ - плотность среды
В твердых телах скорость звука определяется так :
(1.26)
Слайд 35 Физические характеристики звука.
Скорость звука
Длина волны звука
Частота звука
Интенсивность
звуковой волны
Слайд 36 Поток энергии.
Интенсивность волны.
S
∆v
Выделим объем среды, в котором распространяется волна
Количественной
характеристикой
переносимой энергии
волной является
поток
энергии Ф- средняя объемная плотность энергии
[Ф] = 1 Вт
(1.27)
(1.28)
Слайд 37Поток энергии волн, отнесенный к площади поверхности, ориентированной
перпендикулярно направлению распространения
волн называют плотностью
потока энергии волн или интенсивностью
[ I ] =
Вт/м2Энергия, переносимая упругой волной складывается из потенциальной
энергии деформации и кинетической энергии колеблющихся частиц
среды.
- вектор Умова
Если имеется источник звука, то интенсивность волны на некотором расстоянии от него определяется так :
(1.29)
(1.30)
(1.31)
Pист – мощность источника
R – расстояние до точки
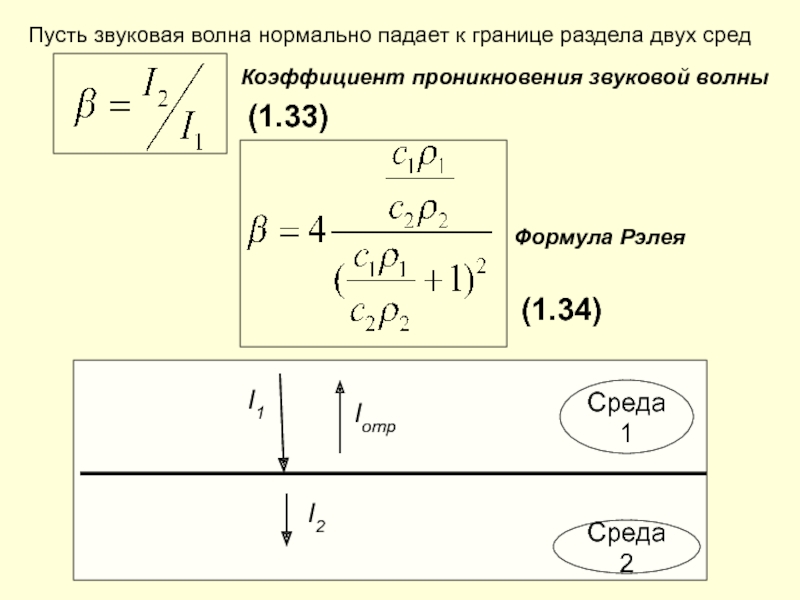
Слайд 38Удельный акустический импеданс.
с – скорость звуковой волны
ρ
– плотность среды
волновое сопротивление (для плоской волны)
[ Z
] = Кг* м -2 * с -1(1.32)
Волновое сопротивление – это характеристика среды,
определяющая условия отражения и преломления
звуковых волн на границе раздела двух сред.
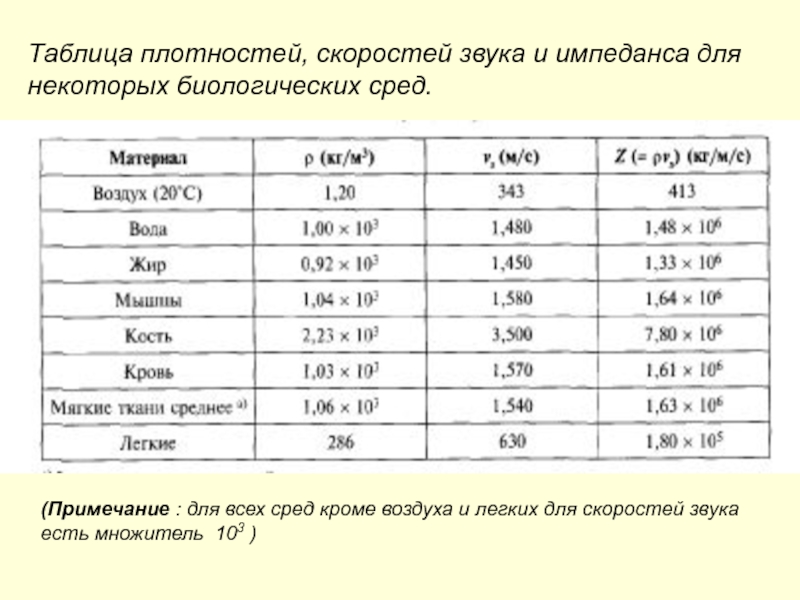
Слайд 39Таблица плотностей, скоростей звука и импеданса для
некоторых биологических сред.
(Примечание
: для всех сред кроме воздуха и легких для скоростей
звукаесть множитель 103 )