Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механика жидкости
Содержание
- 1. Механика жидкости
- 2. Чем отличаются газообразные тела от жидких?
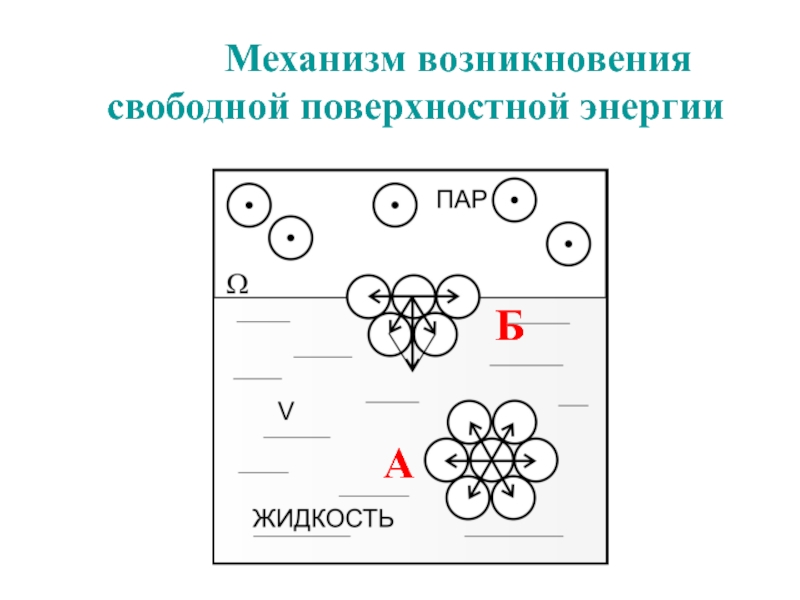
- 3. Механизм возникновения свободной поверхностной энергииАБ
- 4. Поверхностное натяжение Молекулы жидкости располагаются близко друг к
- 5. Каждая молекула испытывает притяжение со стороны всех
- 6. Если же молекула находится на расстоянии от
- 7. Для перехода молекулы из глубины жидкости в
- 8. Итак, молекулы в поверхностном слое обладают дополнительной
- 9. Положение равновесия отвечает минимуму потенциальной энергии, поэтому
- 10. Поверхностная энергия, отнесенная к единице площади поверхности, называется поверхностным натяжением.
- 11. Большие капли жидкости сплющиваются под действием сил
- 12. Рассмотрим часть поверхности жидкости, ограниченную замкнутым контуром.
- 13. Под действием сил
- 14. Значит, коэффициент поверхностного натяжения равен силе
- 15. Чтобы вытащить некоторое количество молекул
- 16. Слайд 16
- 17. Слайд 17
- 18. Поверхностное натяжение зависит:1. Природы жидкости;2. Температуры; ↓
- 19. Слайд 19
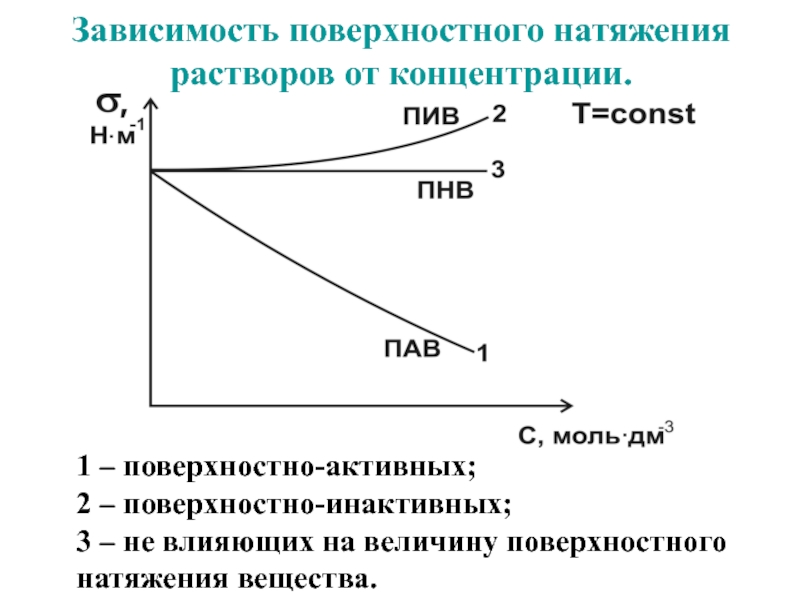
- 20. Зависимость поверхностного натяжения растворов от концентрации.1 –
- 21. Слайд 21
- 22. Механизм удаления грязи с помощью мыльной водыПрямыми
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
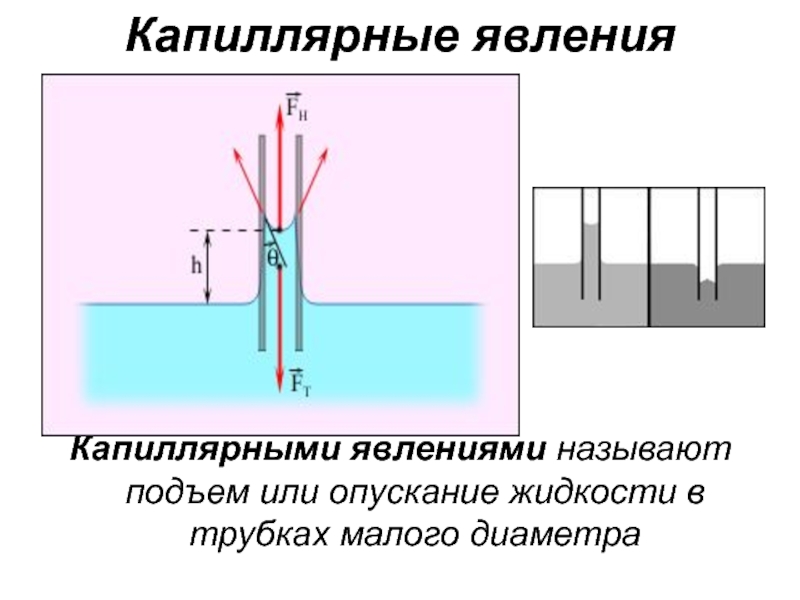
- 26. Капиллярные явленияКапиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра
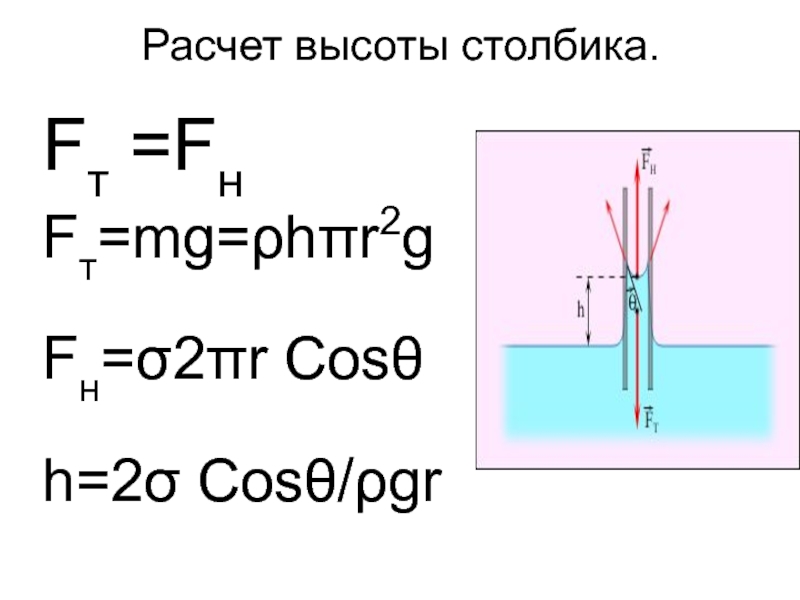
- 27. Расчет высоты столбика.Fт =FнFт=mg=ρhπr2gFн=σ2πr Cosθh=2σ Cosθ/ρgr
- 28. Гидростатическое давлениеСила давления снизу должна уравновешивать вес
- 29. Линии тока Это воображаемые линии, которые проводятся
- 30. Т.к. вектор υ касателен к линиям тока,
- 31. Уравнение БернуллиТак как жидкость несжимаема, т.е. ρ=Const,
- 32. следствия, вытекающие из уравнения Бернулли Для горизонтально
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4 Поверхностное натяжение
Молекулы жидкости располагаются близко друг к другу, поэтому силы
притяжения между ними
имеют значительную величину.
Взаимодействие между молекулами быстро убывает
с расстоянием, начиная с некоторого расстояния r (радиус молекулярного действия) силами притяжения между молекулами можно пренебречь. Радиус r имеет величину порядка 10-9 м, то есть нескольких эффективных диаметров молекулы.
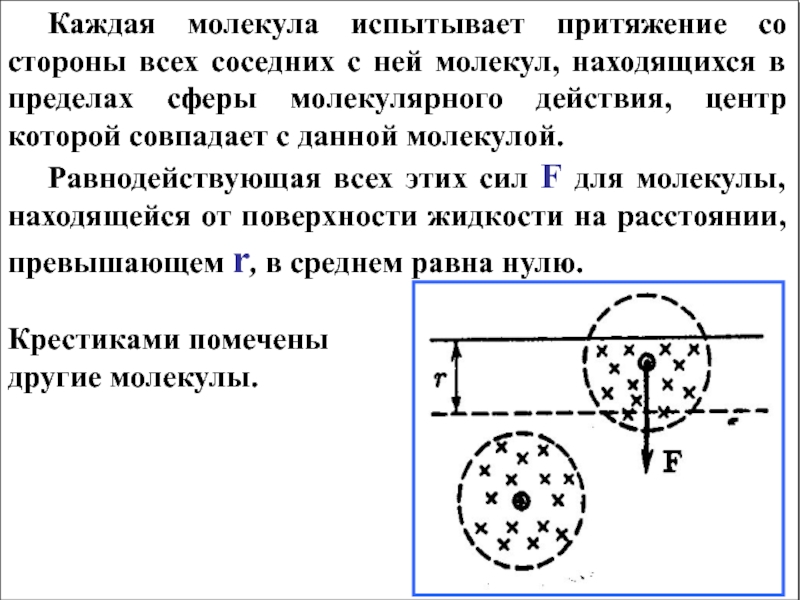
Слайд 5 Каждая молекула испытывает притяжение со стороны всех соседних с ней
молекул, находящихся в пределах сферы молекулярного действия, центр которой совпадает
с данной молекулой.Равнодействующая всех этих сил F для молекулы, находящейся от поверхности жидкости на расстоянии, превышающем r, в среднем равна нулю.
Крестиками помечены
другие молекулы.
Слайд 6 Если же молекула находится на расстоянии от поверхности, меньшем r,
то вследствие того, что плотность пара (или газа, с которым
граничит жидкость) во много раз меньше плотности жидкости, выступающая за пределы жидкости часть сферы молекулярного действия будет менее заполнена молекулами, чем остальная часть сферы.В результате на каждую молекулу, находящуюся в поверхностном слое толщиной r, будет действовать сила F, направленная внутрь жидкости. Величина этой силы растет в направлении от внутренней к наружной границе слоя.
Слайд 7 Для перехода молекулы из глубины жидкости в поверхностный слой она
должна совершить работу против действующих в поверхностном слое сил. Эта
работа совершается молекулой за счет запаса ее кинетической энергии теплового движения и идет на увеличение потенциальной энергии молекулы.При обратном переходе молекулы в глубь жидкости потенциальная энергия, которой обладала молекула в поверхностном слое, переходит в кинетическую энергию молекулы.
Слайд 8 Итак, молекулы в поверхностном слое обладают дополнительной потенциальной энергией. Ее
называют поверхностной энергией, она пропорциональна площади слоя S
Е = S (1) где - коэффициент поверхностного натяжения.
Поверхностная энергия, отнесенная к единице площади поверхности, называется поверхностным натяжением.
Слайд 9 Положение равновесия отвечает минимуму потенциальной энергии, поэтому жидкость, предоставленная самой
себе, принимает форму с минимальной поверхностью, т. е. форму шара.
В поле сил земного тяготения жидкость принимает форму, соответствующую минимуму полной энергии - энергии в поле сил тяготения и поверхностной энергии.
При увеличении размеров тела объем растет как куб линейных размеров, а поверхность - только как квадрат. Поэтому пропорциональная объему тела энергия в поле тяготения изменяется с размерами тела быстрее, чем поверхностная энергия. У малых капель жидкости преобладающую роль играет поверхностная энергия, вследствие чего такие капли имеют форму, близкую к сферической.
Слайд 10Поверхностная энергия, отнесенная к единице площади поверхности, называется поверхностным натяжением.
Слайд 11 Большие капли жидкости сплющиваются под действием сил тяготения, несмотря на
то, что их поверхностная энергия возрастает.
Большие маcсы жидкости принимают
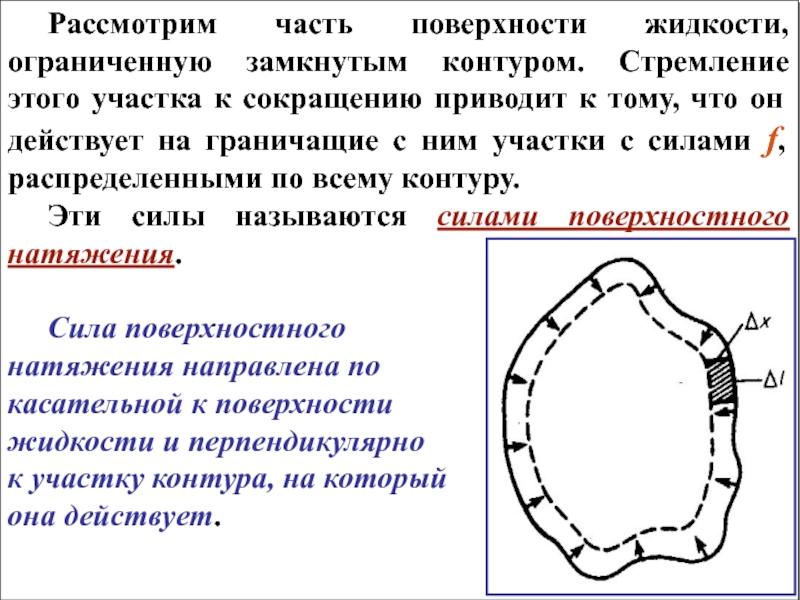
форму сосуда, в который они налиты, с горизонтальной свободной поверхностью. Из-за наличия поверхностной энергии жидкость стремится к сокращению своей поверхности.Слайд 12 Рассмотрим часть поверхности жидкости, ограниченную замкнутым контуром. Стремление этого участка
к сокращению приводит к тому, что он действует на граничащие
с ним участки с силами f, распределенными по всему контуру.Эти силы называются силами поверхностного натяжения.
Сила поверхностного
натяжения направлена по
касательной к поверхности
жидкости и перпендикулярно
к участку контура, на который
она действует.
Слайд 13 Под действием сил поверхностного натяжения
f поверхность жидкости сокращается, а контур уменьшается, смещаясь в
каждой точке контура на величину х.Силы поверхностного натяжения f при перемещении малого участка контура l совершают работу
А = f l х = f S
где S - площадь поверхности, которую пересек участок контура l при своем перемещении.
Данная работа совершается за счет уменьшения поверхностной энергии
А = Е
Сравнивая с (18.4.1) , находим
f =
Слайд 14 Значит, коэффициент поверхностного натяжения равен силе поверхностного натяжения, приходящейся
на единицу длины контура, его размерность
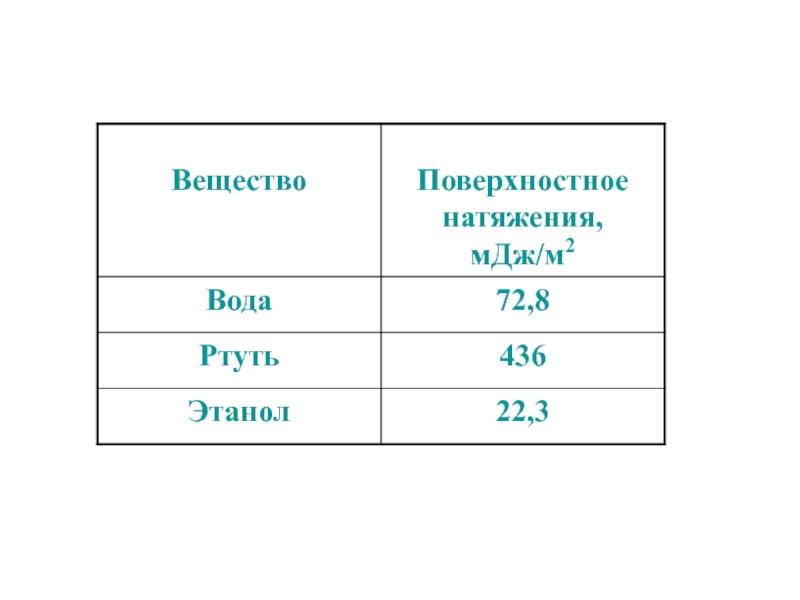
[] = Н/м У большинства жидкостей при Т = 300 К
= 10-2 – 10-1 Н/м
Величина коэффициента поверхностного натяжения зависит от природы жидкости, примесей и от условий, в которых она находится, в том числе от температуры.
Вещества, ослабляющие поверхностное натяжение жидкости, называются поверхностно-активными.
Для воды таким веществом является мыло. Оно уменьшает поверхностное натяжение воды с 7.5*10-2 – 4.5*10-2 Н/м.
Слайд 15 Чтобы вытащить некоторое количество молекул из глубины жидкости на
поверхность, надо затратить положительную работу внешних сил пропорциональную изменению площади поверхности.
∆Авнеш=σ∆S
σ-коэффициент поверхностного натяжения
[1 Н/м = 1 Дж/м2 ]
Поверхностное натяжение
Слайд 18Поверхностное натяжение зависит:
1. Природы жидкости;
2. Температуры; ↓ , Т↑
3. Давления;
↓ , р↑
4. Природы и концентрации растворенных веществ (могут ↓
, ↑ и не влиять).Слайд 20Зависимость поверхностного натяжения растворов от концентрации.
1 – поверхностно-активных;
2 – поверхностно-инактивных;
3
– не влияющих на величину поверхностного натяжения вещества.
Слайд 22Механизм удаления грязи с помощью мыльной воды
Прямыми измерениями установлено, что
поверхностное натяжение воды понижается в два с половиной раза при
добавлении мыла: от 7*10-2 до 3*10-2 Дж/м2Слайд 26Капиллярные явления
Капиллярными явлениями называют подъем или опускание жидкости в трубках
малого диаметра
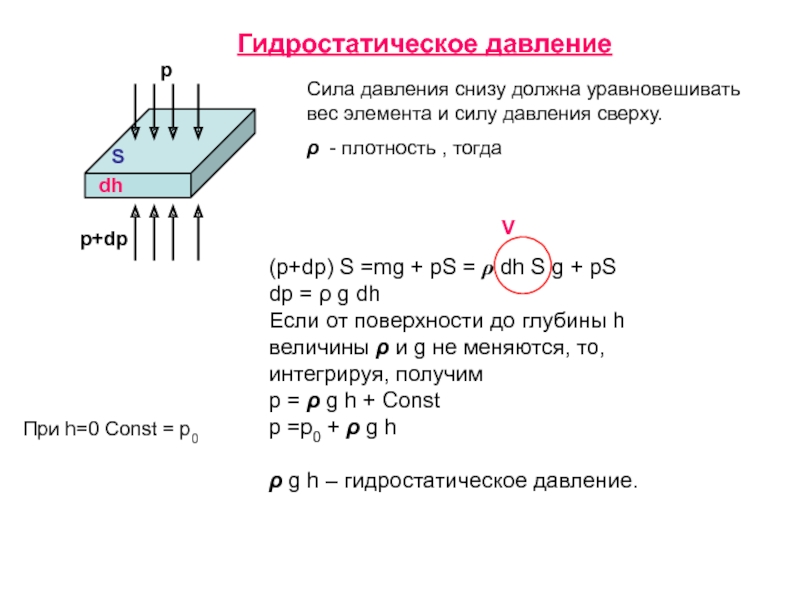
Слайд 28Гидростатическое давление
Сила давления снизу должна уравновешивать вес элемента и силу
давления сверху.
ρ - плотность , тогда
(p+dp) S =mg
+ pS = ρ dh S g + pSdp = ρ g dh
Если от поверхности до глубины h величины ρ и g не меняются, то, интегрируя, получим
p = ρ g h + Const
p =p0 + ρ g h
ρ g h – гидростатическое давление.
V
При h=0 Const = p0
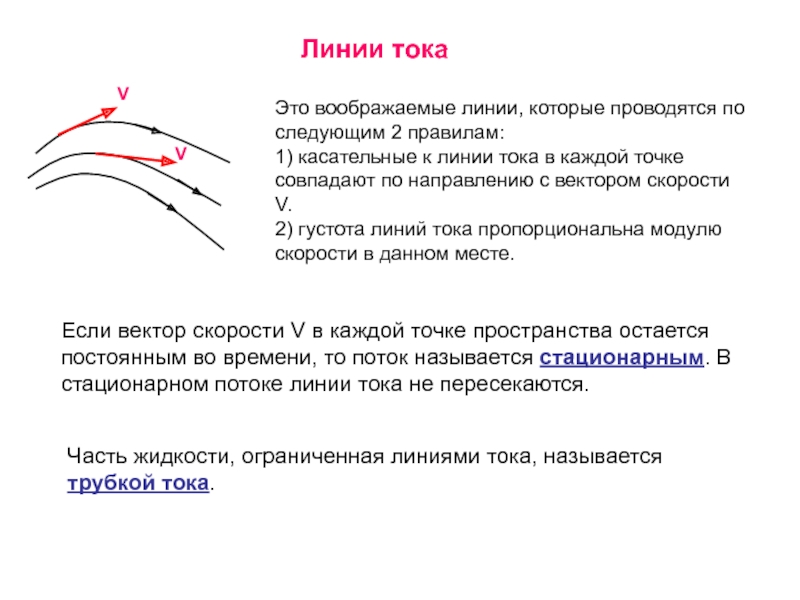
Слайд 29Линии тока
Это воображаемые линии, которые проводятся по следующим 2
правилам:
1) касательные к линии тока в каждой точке совпадают по
направлению с вектором скорости V.2) густота линий тока пропорциональна модулю скорости в данном месте.
Если вектор скорости V в каждой точке пространства остается постоянным во времени, то поток называется стационарным. В стационарном потоке линии тока не пересекаются.
Часть жидкости, ограниченная линиями тока, называется трубкой тока.
Слайд 30Т.к. вектор υ касателен к линиям тока, он будет касателен
и к поверхности трубки тока. При этом частицы жидкости при
своем движении не пересекают стенок трубки тока.За время Δt через сечение S пройдет объем жидкости ΔV = S υ Δt.
ΔV1= S1υ1 Δt.
ΔV2= S2υ2 Δt
Так как жидкость несжимаема и через стенки трубки тока не проходит
ΔV1= ΔV2
S1υ1 = S2υ2
уравнение неразрывности струи
Для несжимаемой жидкости величина произведения S· υ в любом сечении одной и той же трубки тока должна быть одинакова
Слайд 31Уравнение Бернулли
Так как жидкость несжимаема, т.е. ρ=Const, а через стенки
трубки тока жидкость уйти не может
ΔV1= ΔV2 = ΔV. A = p1S1 Δl1 – p2S2 Δl2 = (p1 - p2) ΔV
работа сил, приложенных к сечениям S1 и S2.
Уравнение Бернулли
в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие:
Слайд 32следствия, вытекающие из уравнения Бернулли
Для горизонтально расположенной линии тока
h2 = h1 справедливо:
S1υ1 = S2υ2
т.е давление меньше в тех
точках, где скорость большеЕсли S2>S1, то υ2< υ1, следовательно р2>p1