Метод Гаусса — Жордана

Содержание

1. Метод Гаусса — Жордана
2. Метод Гаусса — ЖорданаМетод Гаусса — Жордана
3. Алгоритм 1.Выбирают первый слева столбец
4. Алгоритм
5. Слайд 5
6. Пример
7. Слайд 7
8. Слайд 8
9. Слайд 9
10. Слайд 10
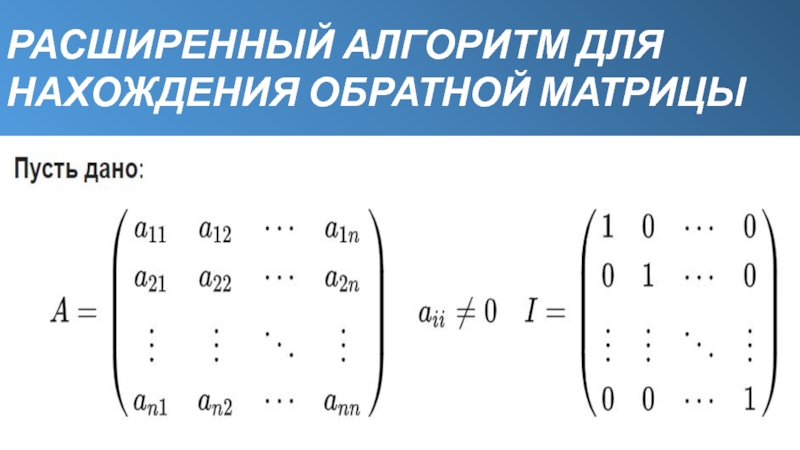
11. Расширенный алгоритм для нахождения обратной матрицы
12. Прямой ход (алгоритм образования нулей под главной диагональю)
13. Прямой ход (алгоритм образования нулей под главной диагональю)
14. Слайд 14
15. Обратный ход (алгоритм образования нулей над главной диагональю)
16. Спасибо за внимание!
17. Скачать презентанцию

Метод Гаусса — ЖорданаМетод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или

Главная
Разное
Метод Гаусса — Жордана

Слайды и текст этой презентации

Слайд 1 Метод Гаусса — Жордана

Слайд 2Метод Гаусса — Жордана
Метод Гаусса — Жордана (метод полного исключения

неизвестных) — метод, который используется для решения систем линейных алгебраических

уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана

Метод Гаусса — ЖорданаМетод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения

Слайд 3 Алгоритм
1.Выбирают первый слева столбец матрицы, в котором есть

хоть одно отличное от нуля значение. (разрешающий-главный столбец)
2.Если самое верхнее

число в этом столбце ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.
3.Все элементы первой (разрешающей-главной) строки делят на верхний (разрешающий-главный) элемент выбранного столбца.

Алгоритм 1.Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.

Слайд 4 Алгоритм
4.Из оставшихся строк вычитают первую

(разрешающую-главную) строку, умноженную на первый элемент соответствующей строки, с целью

получить первым элементом каждой строки (кроме первой) ноль.
5.Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.
6.После повторения этой процедуры (n-1) раз , получают верхнюю треугольную матрицу

Алгоритм 4.Из оставшихся строк вычитают первую (разрешающую-главную) строку, умноженную на первый

Слайд 5 Алгоритм
7.Вычитают из предпоследней строки

последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в

предпоследней строке осталась только 1 на главной диагонали.
8.Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).