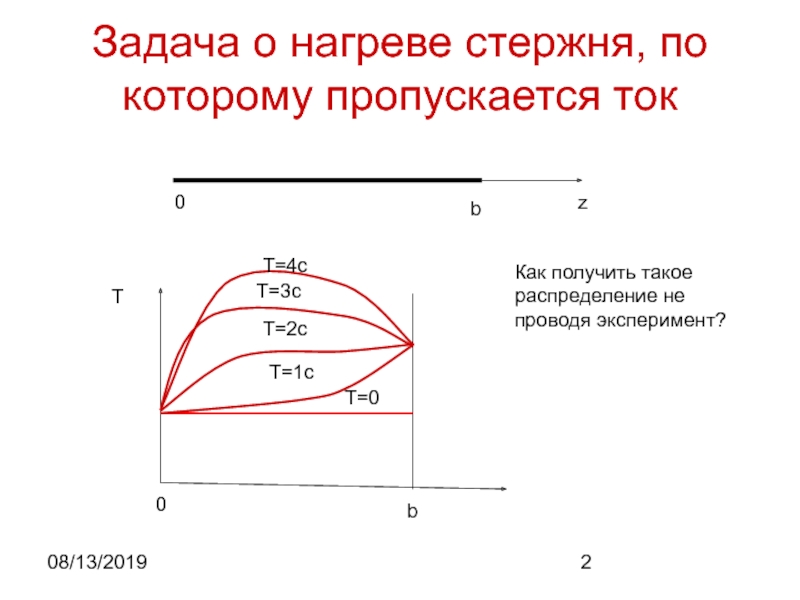
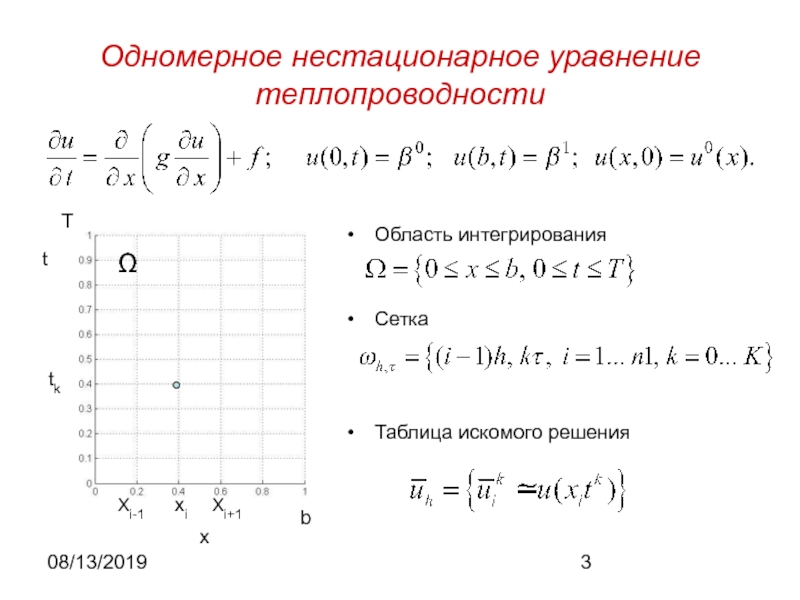
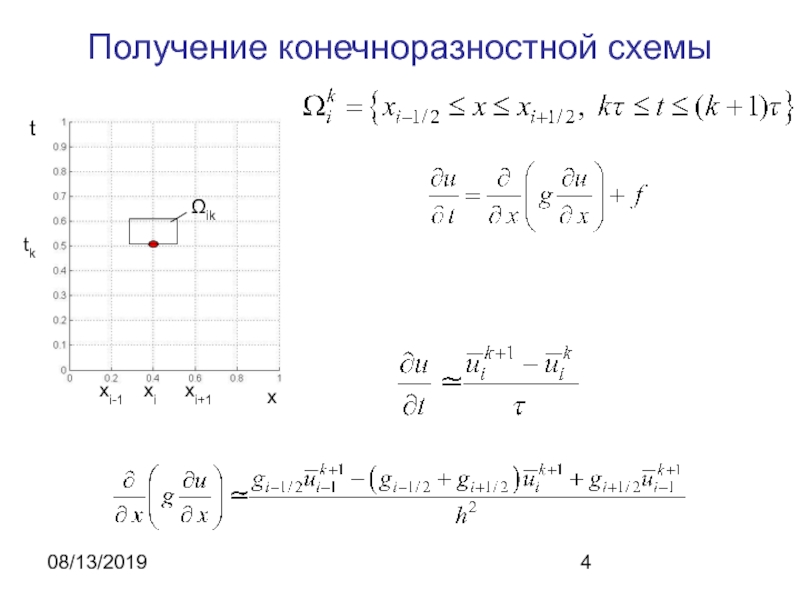
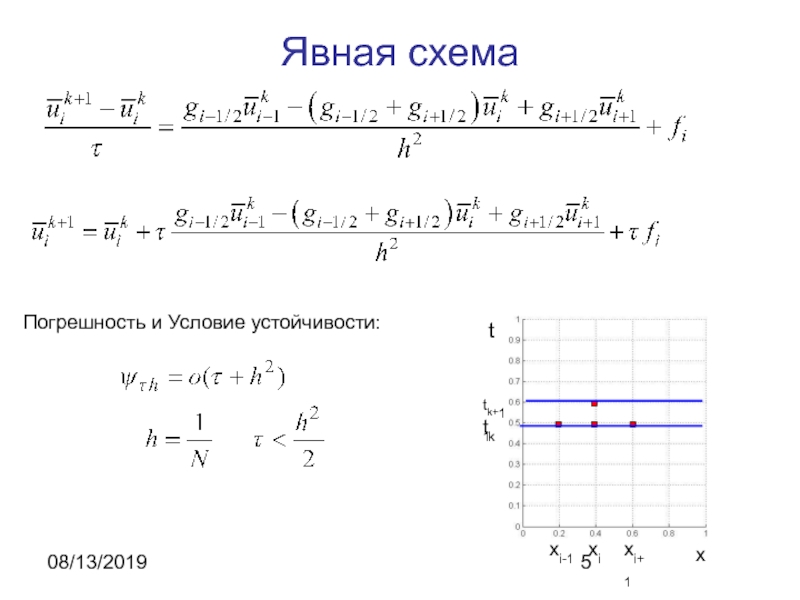
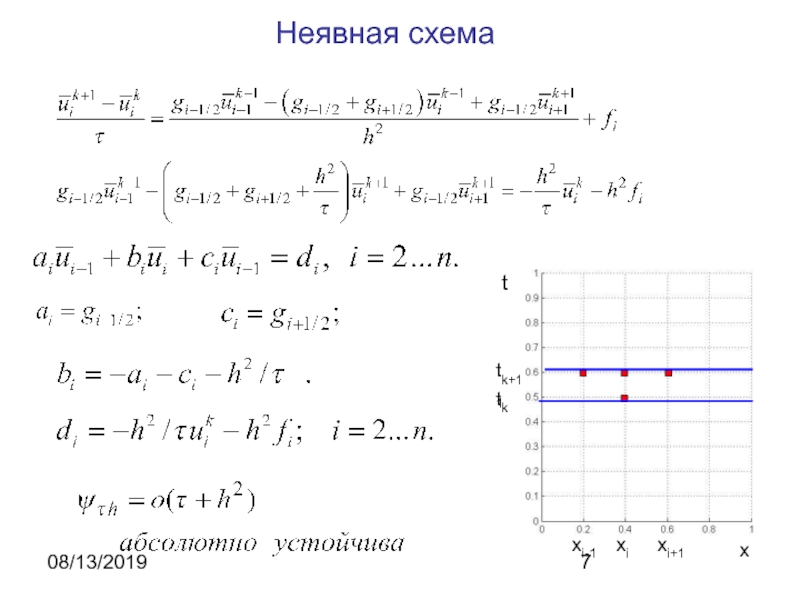
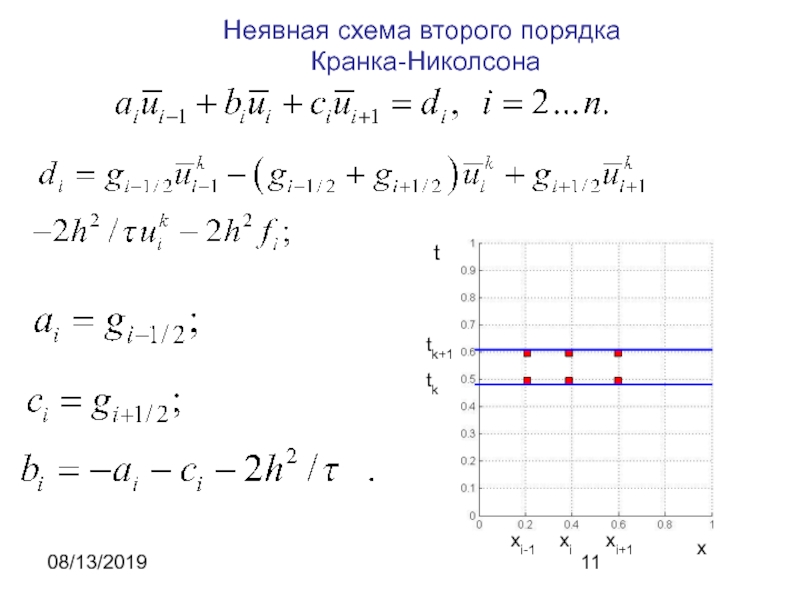
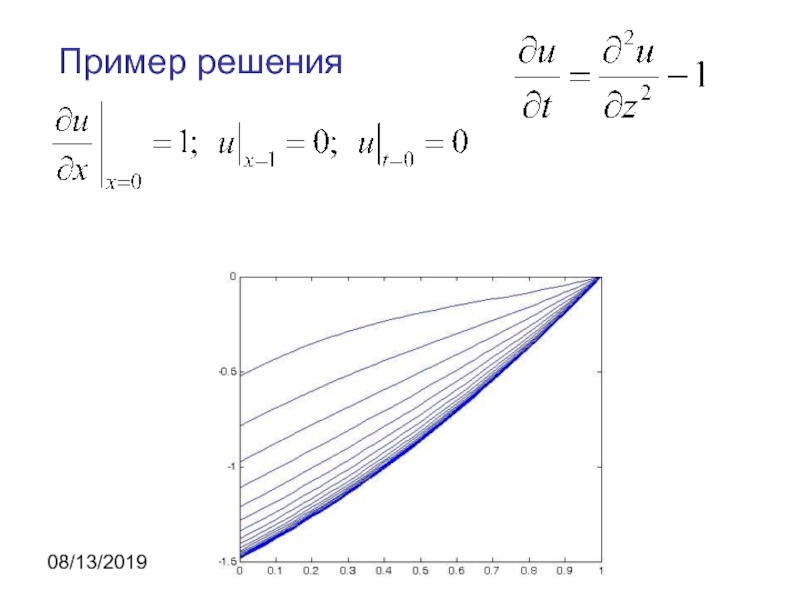
нестационарное уравнение теплопроводности:
Явная и неявная схемы
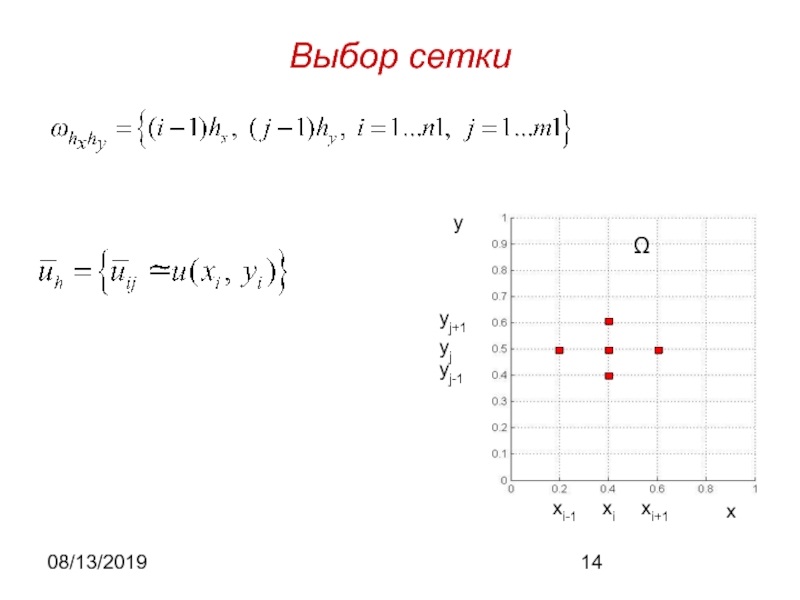
Задача Дирихле для двумерного уравнения
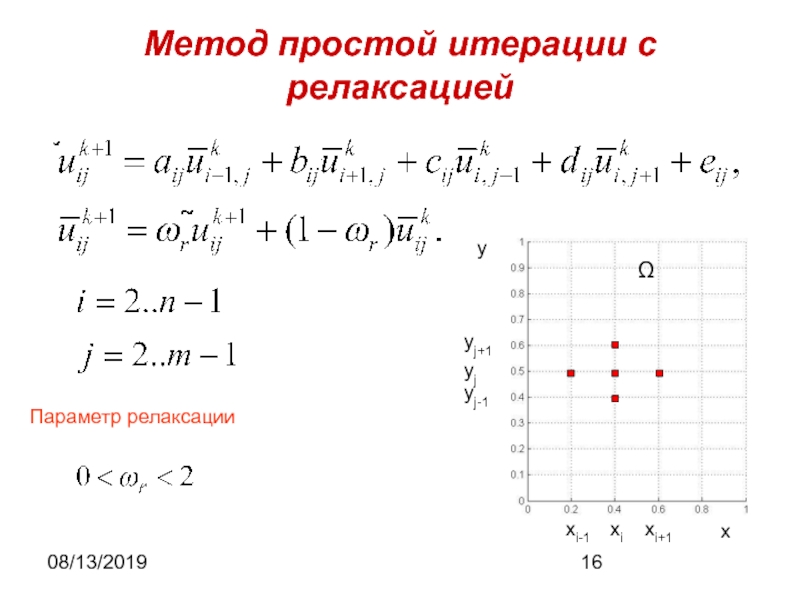
Пуассона Метод простой итерации с релаксацией
Метод Зейделя
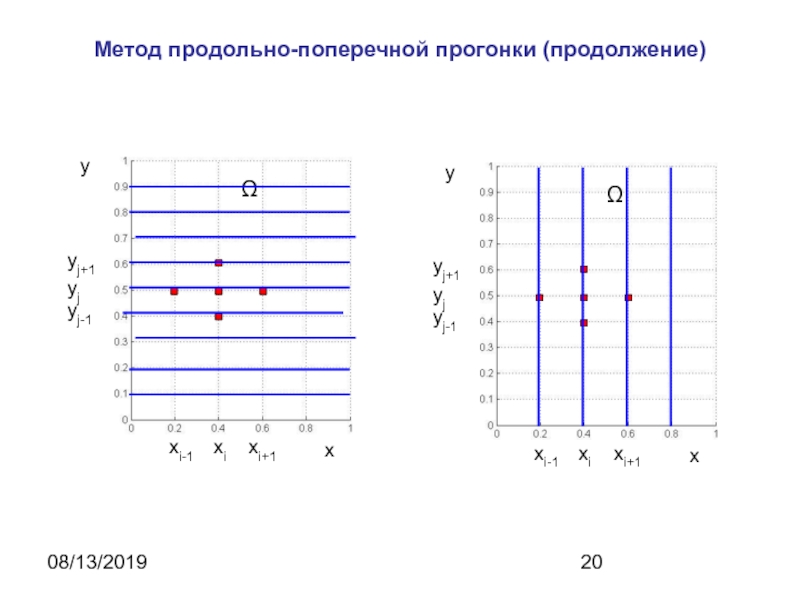
Метод продольно-поперечной прогонки