Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы кластеризации
Содержание
- 1. Методы кластеризации
- 2. План лекцииВведениеФормальная постановка задачиМетод k-среднихМетод ISODATAАгломеративный методДивизимный метод
- 3. ВведениеЗадача кластеризации состоит в разделении исследуемого множества
- 4. ВведениеКластеризация отличается от классификации тем, что этап
- 5. ВведениеЭта задача решается на начальных этапах исследования,
- 6. ВведениеКластерный анализ позволяет рассматривать достаточно большой объем
- 7. Формальная постановка задачиДано множество данных, состоящее из
- 8. Формальная постановка задачиТаким образом, i-й объект можно
- 9. Формальная постановка задачиТребуется:найти способ сравнения d(Sp, Sq)
- 10. Формальная постановка задачиВ качестве меры сходства используются:евклидово расстояниеквадрат евклидова расстояниярасстояние Хэммингарасстояние Чебышева
- 11. Формальная постановка задачиМетоды кластерного анализа можно разделить на две группы:неиерархическиеиерархические
- 12. Метод k-среднихНеиерархическим методом кластеризации является метод k-средних (k-means)Предварительно необходимо выбрать вероятное число кластеров k
- 13. Метод k-средних1. Выбирается k произвольных исходных центров
- 14. Метод k-среднихВыбор числа кластеров является сложным вопросомЕсли
- 15. Метод k-среднихНачальный выбор центров кластеров осуществляется следующим
- 16. Метод k-среднихЦентры кластеров вычисляются по формулам: …где NC – количество объектов, входящих в кластер С
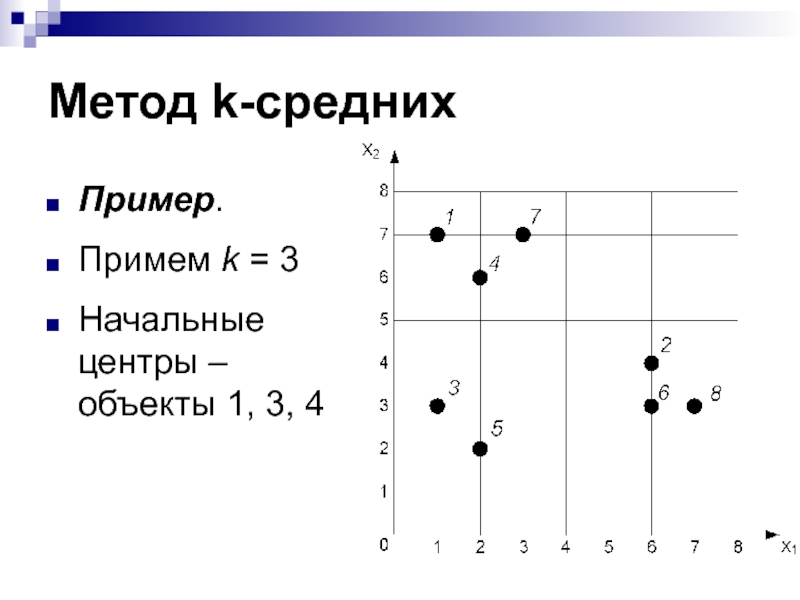
- 17. Метод k-среднихПример. Примем k = 3Начальные центры – объекты 1, 3, 4
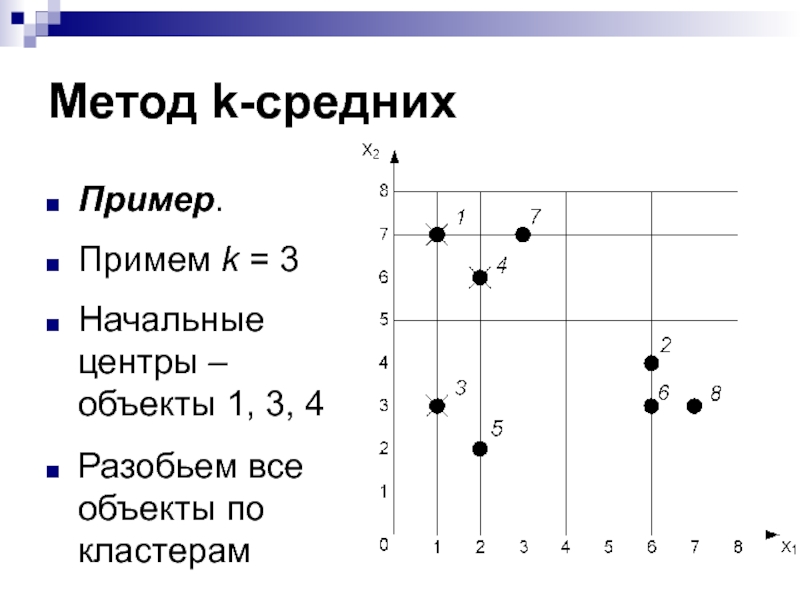
- 18. Метод k-среднихПример. Примем k = 3Начальные центры – объекты 1, 3, 4Разобьем все объекты по кластерам
- 19. Метод k-среднихНайдем новые центры кластеров
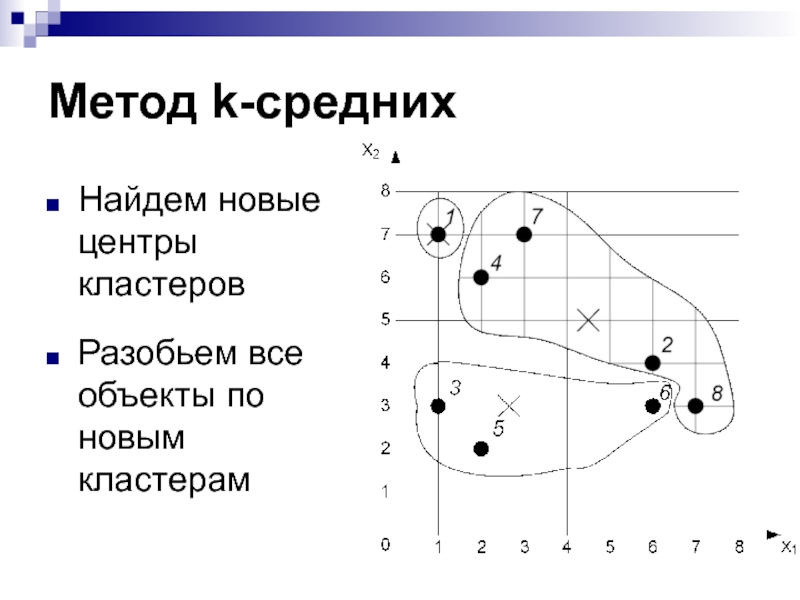
- 20. Метод k-среднихНайдем новые центры кластеровРазобьем все объекты по новым кластерам
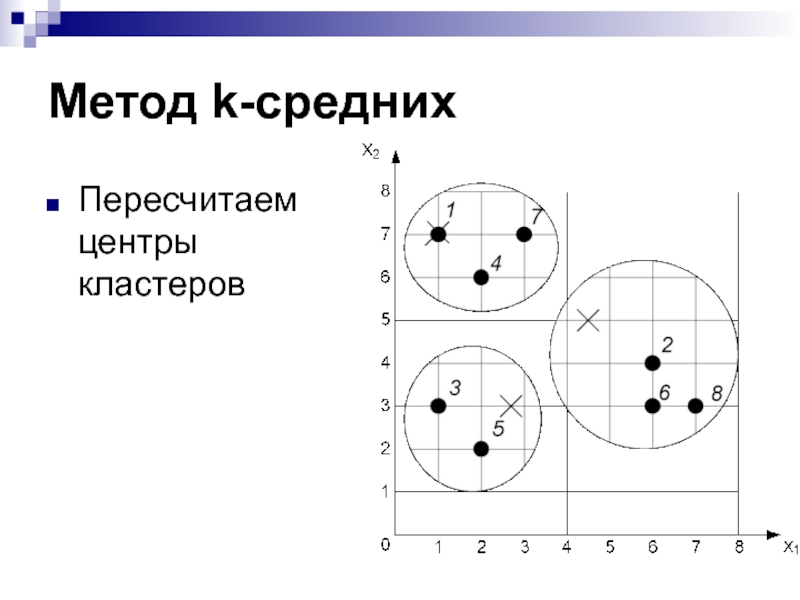
- 21. Метод k-среднихПересчитаем центры кластеров
- 22. Метод k-среднихРазбивка объектов по новым кластерам не меняет расположение центров
- 23. Метод ISODATAISODATA – Iterative Self-Organizing Data Analysis
- 24. Метод ISODATAЕсли в кластер входит менее заданного
- 25. Метод ISODATAЕсли расстояние между центрами двух кластеров
- 26. Иерархические методыК иерархическим методам кластеризации относятся:агломеративный алгоритм (Agglomerative Nesting, AGNES)дивизимный алгоритм (Divisive ANAlysis, DIANA)
- 27. Агломеративный методВ начале работы алгоритма все объекты
- 28. Агломеративный методРасстояние между кластерами можно определить различными
- 29. Агломеративный методПример. Каждый объект формирует свой кластер
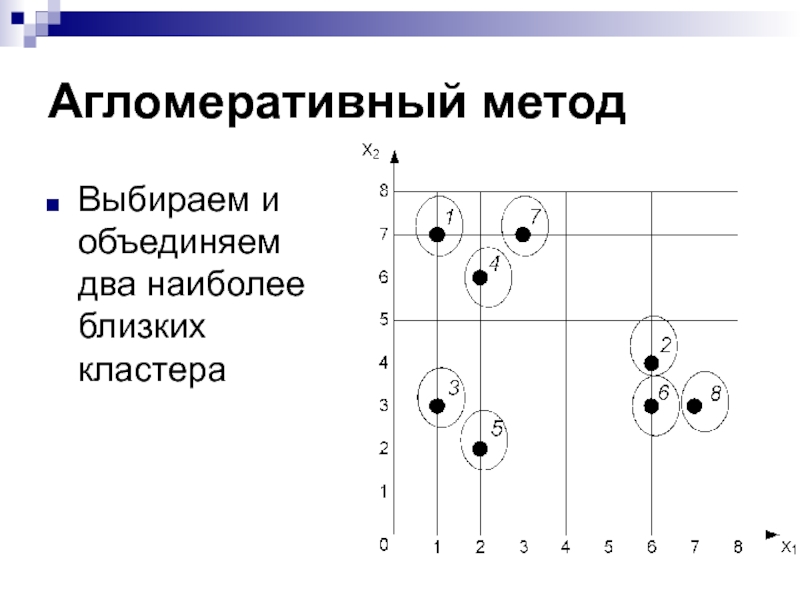
- 30. Агломеративный методВыбираем и объединяем два наиболее близких кластера
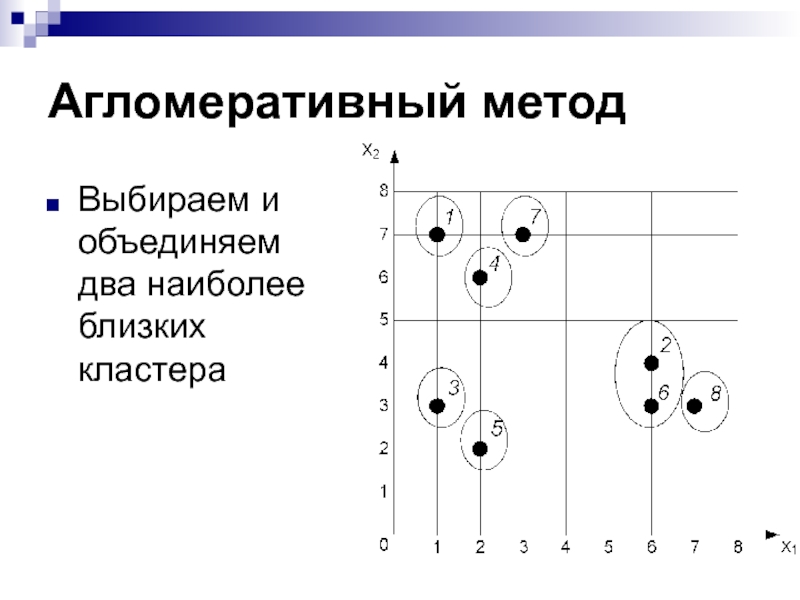
- 31. Агломеративный методВыбираем и объединяем два наиболее близких кластера
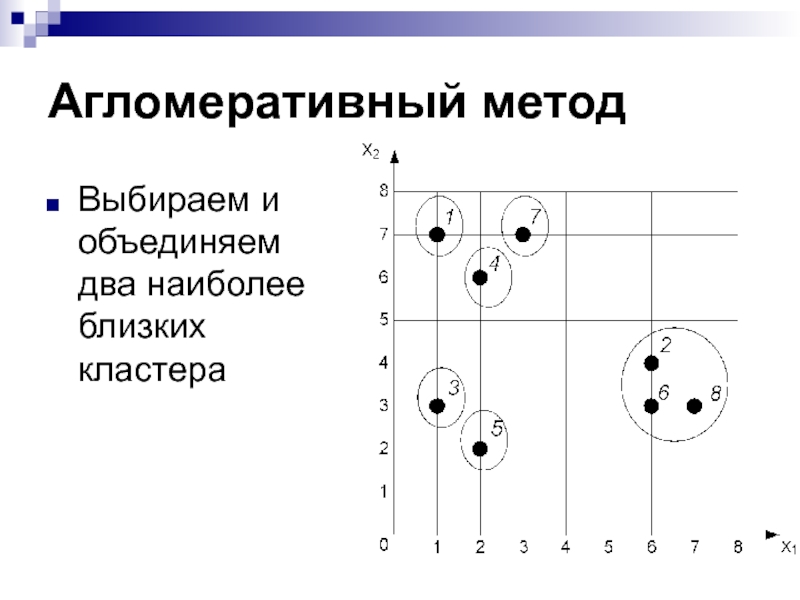
- 32. Агломеративный методВыбираем и объединяем два наиболее близких кластера
- 33. Дивизимный методНа первом шаге все объекты помещаются
- 34. Дивизимный методВыбранный объект удаляется из кластера С1
- 35. Дивизимный методПереносы элементов из С1 в С2
- 36. Дивизимный методВ результате один кластер делится на
- 37. Дивизимный методКластер для расщепления выбирается, например, по
- 38. Иерархические методы
- 39. Иерархические методыПроблема определения оптимального числа кластеров:иногда можно
- 40. Иерархические методыВ иерархических методах существует способ, позволяющий
- 41. Иерархические методыСкачкообразное увеличение критерия Е говорит о
- 42. Скачать презентанцию
План лекцииВведениеФормальная постановка задачиМетод k-среднихМетод ISODATAАгломеративный методДивизимный метод
Слайды и текст этой презентации
Слайд 2План лекции
Введение
Формальная постановка задачи
Метод k-средних
Метод ISODATA
Агломеративный метод
Дивизимный метод
Слайд 3Введение
Задача кластеризации состоит
в разделении исследуемого множества объектов на группы «похожих»
объектов, называемых кластерами
Слайд 4Введение
Кластеризация отличается
от классификации тем, что этап обучения на примерах отсутствует
В
задачах классификации множество классов заранее известно, в кластеризации классы определяются в процессе
анализаПоэтому кластеризация относится к задачам обучения без учителя (unsupervised learning)
Слайд 5Введение
Эта задача решается на начальных этапах исследования, когда о данных
мало что известно
Ее решение помогает лучше понять данные
После определения кластеров
применяются другие методы Data Mining, чтобы попытаться установить,
что означает такое разбиение
Слайд 6Введение
Кластерный анализ позволяет рассматривать достаточно большой объем информации и сжимать
большие массивы информации,
делать их компактными и наглядными
Слайд 7Формальная постановка задачи
Дано множество данных, состоящее из N объектов (векторов):
S1,
S2, …, SN
Каждый объект описывается набором признаков:
x1, x2, …, xm,
где
m – размерность пространства признаков
Слайд 8Формальная постановка задачи
Таким образом, i-й объект можно записать в виде:
Si
= (xi1, xi2, …, xim)
Класс для каждого объекта неизвестен
Слайд 9Формальная постановка задачи
Требуется:
найти способ сравнения d(Sp, Sq)
объектов между собой (меру
сходства, функцию расстояния)
определить множество кластеров
С1, C2, …, Cr
причем количество кластеров
r – неизвестноразбить данные по кластерам
Слайд 10Формальная постановка задачи
В качестве меры сходства используются:
евклидово расстояние
квадрат евклидова расстояния
расстояние
Хэмминга
расстояние Чебышева
Слайд 11Формальная постановка задачи
Методы кластерного анализа можно разделить на две группы:
неиерархические
иерархические
Слайд 12Метод k-средних
Неиерархическим методом кластеризации является метод k-средних (k-means)
Предварительно необходимо выбрать
вероятное число кластеров k
Слайд 13Метод k-средних
1. Выбирается k произвольных исходных центров кластеров – обычно
выбираются k объектов
2. Все объекты разбиваются на k групп, наиболее
близких к одному из центров3. Вычисляются новые центры кластеров
4. Проводится новое разбиение всех объектов на основании близости к новым центрам
Шаги 3 и 4 повторяются до тех пор, пока центры кластеров не перестанут меняться или пока не достигнуто максимальное число итераций
Слайд 14Метод k-средних
Выбор числа кластеров является сложным вопросом
Если нет предположений относительно
этого числа, рекомендуют создать 2 кластера, затем 3, 4, 5
и т. д., сравнивая полученные результаты
Слайд 15Метод k-средних
Начальный выбор центров кластеров осуществляется следующим образом:
выбор k объектов
для максимизации начального расстояния
случайный выбор k объектов
выбор первых k объектов
Слайд 16Метод k-средних
Центры кластеров вычисляются
по формулам:
…
где NC – количество объектов,
входящих в кластер С
Слайд 18Метод k-средних
Пример.
Примем k = 3
Начальные центры – объекты 1,
3, 4
Разобьем все объекты по кластерам
Слайд 23Метод ISODATA
ISODATA – Iterative Self-Organizing Data Analysis Techniques – итеративный
самоорганизующийся метод анализа данных
Более сложный алгоритм, чем k-means, дополненный несколькими
эвристикамиПолное описание см. Ту Дж., Гонсалес Р. «Принципы распознавания образов», М.: Мир, 1978
Слайд 24Метод ISODATA
Если в кластер входит менее заданного минимального числа объектов,
кластер удаляется
Если среднее расстояние между объектами кластера больше заданного максимального
порога, кластер расщепляется на два новых кластера
Слайд 25Метод ISODATA
Если расстояние между центрами двух кластеров меньше заданного минимального
порога, кластеры сливаются
В алгоритме ISODATA множество параметров, настройка которых представляет
определенные трудности
Слайд 26Иерархические методы
К иерархическим методам кластеризации относятся:
агломеративный алгоритм (Agglomerative Nesting, AGNES)
дивизимный
алгоритм
(Divisive ANAlysis, DIANA)
Слайд 27Агломеративный метод
В начале работы алгоритма все объекты являются отдельными кластерами
На
первом шаге наиболее похожие (близкие) два кластера объединяются в дин
кластерНа последующих шагах объединение продолжается до тех пор, пока все объекты не будут составлять один кластер
На любом этапе объединение можно прервать, получив нужное число кластеров
Слайд 28Агломеративный метод
Расстояние между кластерами можно определить различными способами:
расстояние между центрами
кластеров
расстояние между двумя наиболее близкими объектами в кластерах
расстояние между двумя
наиболее дальними объектами в кластерахсреднее расстояние между всеми парами объектов в них
Слайд 33Дивизимный метод
На первом шаге все объекты помещаются в один кластер
С1
Выбирается объект, у которого среднее значение расстояния до других объектов
в этом кластере наибольшее:
Слайд 34Дивизимный метод
Выбранный объект удаляется из кластера С1 и формирует первый
элемент второго кластера С2
На каждом последующем шаге объект
в кластере С1,
для которого разность между средним расстоянием до объектов, находящихся в С2 и средним расстоянием до объектов, остающихся в С1, наибольшая, переносится в С2
Слайд 35Дивизимный метод
Переносы элементов из С1 в С2 продолжаются до тех
пор, пока соответствующие разности средних не станут отрицательными, то есть пока существуют
элементы, расположенные к элементам кластера С2 ближе, чем к элементам кластера С1
Слайд 36Дивизимный метод
В результате один кластер делится на два дочерних, один
из которых расщепляется на следующем уровне иерархии
Каждый последующий уровень применяет
процедуру разделения к одному из кластеров, полученных на предыдущем уровне
Слайд 37Дивизимный метод
Кластер для расщепления выбирается, например, по наибольшему диаметру
Диаметр кластера
– расстояние между двумя наиболее дальними объектами кластера
Рекурсивное разделение кластеров
продолжается, пока хотя бы один кластер содержит более одного объекта
Слайд 39Иерархические методы
Проблема определения оптимального числа кластеров:
иногда можно априорно определить число
кластеров
однако в большинстве случаев число кластеров определяется в процессе кластеризации
Слайд 40Иерархические методы
В иерархических методах существует способ, позволяющий определить оптимальное число
кластеров
Процессу группировки объектов в иерархическом кластерном анализе соответствует постепенное возрастание
коэффициента, называемого критерием ЕКритерий Е на каждом шаге определяется как расстояние между ближайшими кластерами
Слайд 41Иерархические методы
Скачкообразное увеличение критерия Е говорит о переходе от сильно
связанного к слабо связанному состоянию объектов
Таким образом, нужно останавливать процесс
разбиения, когда значение критерия Е резко изменится
