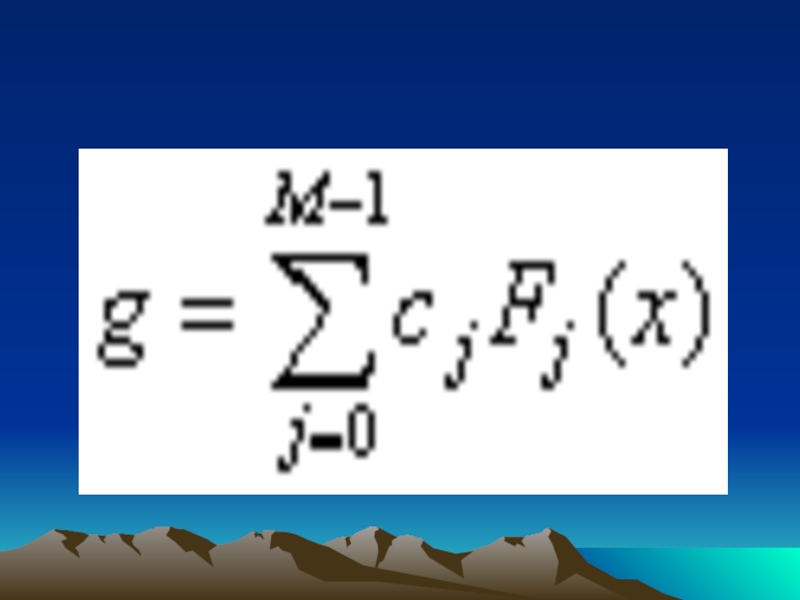Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы линейной алгебры в экономическом анализе Модель Леонтьева многоотраслевой экономики
Содержание
- 1. Методы линейной алгебры в экономическом анализе Модель Леонтьева многоотраслевой экономики
- 2. Балансовые таблицыДля наглядного выражения взаимной связи между
- 3. Условия анализаНародное хозяйство разбито на некоторое число
- 4. Условия моделированияИмеется n различных отраслей О1,,..., Оn,
- 5. Исходные данные моделиXi,- общий объем продукции i
- 6. Балансовая таблица
- 7. Баланс отраслейБалансовый характер этой таблицы выражается в
- 8. Формализация балансовой моделиЕдиницы измерения всех указанных величин
- 9. Формализация балансовой моделиВеличины аij=xij/Xj остаются постоянными в
- 10. Формализация балансовой моделиСогласно гипотезе линейности имеемxij =
- 11. Формализация балансовой моделиВ предположении линейности соотношения модели
- 12. Матричная форма моделиX= Ах+у,
- 13. Модель ЛеонтьеваВектор X называется вектором валового выпуска,
- 14. Планирование с помощью балансовой моделиУравнения межотраслевого баланса
- 15. Нужно решить задачу: сколько следует произвести продукции
- 16. Ограничения моделиПри этом нужно иметь в виду
- 17. Продуктивные модели ЛеонтьеваОпределение. Матрица А>0 называется продуктивной,
- 18. Условия продуктивностиТеорема 1 (первый критерий продуктивности). Если
- 19. Условия продуктивностиТеорема 2 (второй критерий продуктивности). Матрица
- 20. Условия продуктивностиТеорема 3 (третий критерий продуктивности). Матрица
- 21. Правила проверки продуктивностиЕсли сумма элементов любого столбца
- 22. Запас продуктивностиПусть А >= 0 - продуктивная
- 23. Модель равновесных цен Рассмотрим теперь балансовую модель,
- 24. Обозначим через p=(p1,p2,рn) - вектор цен, i-я
- 25. Модель равновесных ценЧасть своего дохода эта отрасль
- 26. Модель равновесных ценТогда для выпуска продукции в
- 27. Модель равновесных ценПолучим равенство:X1P1 = X1(a11p1 +
- 28. Модель равновесных ценАналогично получим для остальных отраслейP2
- 29. Модель равновесных ценМодель равновесных цен позволяет, зная
- 30. Метод наименьших квадратовМетод наименьших квадратов (часто называемый
- 31. Общий линейный метод наименьших квадратов При
- 32. Слайд 32
- 33. При этом коэффициенты cj выбираются таким образом,
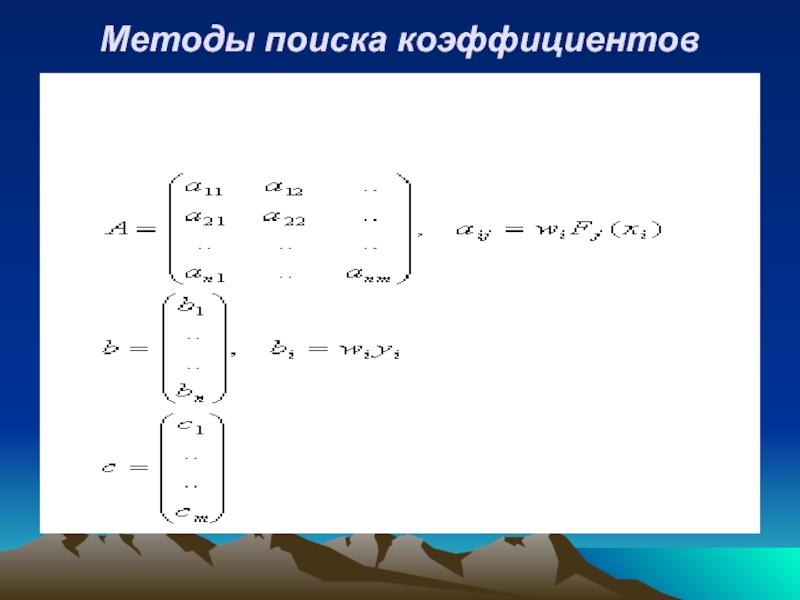
- 34. Методы поиска коэффициентов
- 35. Задачу минимизации функции E можно записать в матричной форме, как поиск
- 36. Скачать презентанцию
Балансовые таблицыДля наглядного выражения взаимной связи между отраслями используются таблицы, которые называются таблицами межотраслевого баланса. Идея таких таблиц была сформулирована в работах советских экономистов, а первая таблица опубликована ЦСУ в 1926
Слайды и текст этой презентации
Слайд 1Методы линейной алгебры в экономическом анализе
Модель Леонтьева многоотраслевой экономики
Балансовый характер
экономики.
Слайд 2Балансовые таблицы
Для наглядного выражения взаимной связи между отраслями используются таблицы,
которые называются таблицами межотраслевого баланса. Идея таких таблиц была сформулирована
в работах советских экономистов, а первая таблица опубликована ЦСУ в 1926 г. Формализованная модель межотраслевого баланса, обеспечивающая широкие возможности анализа, была разработана в 1936 г. Русско- американским экономистом В. Леонтьевым .
Слайд 3Условия анализа
Народное хозяйство разбито на некоторое число и отраслей, которые
производят свой однородный продукт, причем разные отрасли производят разные продукты.
Такое представление является абстракцией, так как в реальной экономике отрасль определяется не только названием выпускаемого продукта, но и ведомственной принадлежностью своих предприятий. Такое представление об отрасли целесообразно, так как позволяет изучить функционирование народного хозяйства «в первом приближении».
Слайд 4Условия моделирования
Имеется n различных отраслей О1,,..., Оn, каждая из которых
производит свой продукт. Отрасль Оi будем коротко называть «i-я отрасль».
В процессе производства своего продукта каждая отрасль нуждается в продукции других отраслей (производственное потребление). Рассмотрит определенный промежуток времени [Т0, Т1] (обычно таким промежутком служит плановый год) и введем следующие обозначения:
Слайд 5Исходные данные модели
Xi,- общий объем продукции i отрасли за данный
промежуток времени - валовой выпуск отрасли i;
xij - объем
продукции отрасли i, расходуемый отраслью j в процессе производства;Yi - объем продукции отрасли i, предназначенный к потреблению в непроизводственной сфере - объем конечного потребления.
Слайд 7Баланс отраслей
Балансовый характер этой таблицы выражается в том, что при
любом i = 1, ..., n должно выполняться соотношение
Xi=xi1+xi2+…….+xin +
Yi, означающее, что валовой выпуск Xi расходуется на производственное потребление, равное хi1 +xi2 + ... +xin, и непроизводственное потребление, равное Yi, называют соотношениями баланса. 
Слайд 8Формализация балансовой модели
Единицы измерения всех указанных величин могут быть или
натуральными (кубометры, тонны, штуки, киловатт-часы и т. п.), или стоимостными.
В зависимости от этого различают натуральный и стоимостной межотраслевой балансы. Будем рассматривать стоимостные балансы.
Слайд 9Формализация балансовой модели
Величины аij=xij/Xj остаются постоянными в течение ряда лет.
Это обусловливается примерным постоянством используемой технологии.
Т.О. для выпуска любого объема
Xj- продукции отрасли j необходимо затратить продукцию отрасли i в количестве aij*Xj.-, где аij - постоянный коэффициент. Материальные издержки пропорциональны объему производимой продукции. Это допущение предполагает линейность существующей технологии. 
Слайд 10Формализация балансовой модели
Согласно гипотезе линейности имеем
xij = aij*Xj (i,j= l,...,n).
Коэффициенты аij называют коэффициентами прямых затрат (коэффициентами материалоемкости).
Слайд 11Формализация балансовой модели
В предположении линейности соотношения модели принимают вид:
Х1 =
а11*x1 + а12*х2 + ... + а1n*хn +Y1
X2 = а12*x1
+ а22*х2 + ... + а2n*хn+Y2…………………………………….
Xn = a1n*x1 +a2n*x2 +… +ann*xn+Yn
Слайд 12Матричная форма модели
X= Ах+у,
a11 a12 a1n
X1 Y1А = а21 а22 ...a2n X = X2 Y = Y2
an1 an2 ann Xn Yn
Слайд 13Модель Леонтьева
Вектор X называется вектором валового выпуска,
вектор Y -
вектором конечного потребления, а матрица А - матрицей прямых затрат.
Соотношение называется уравнением линейного межотраслевого баланса.Данную математическую модель называют моделью Леонтьева.
Слайд 14Планирование с помощью балансовой модели
Уравнения межотраслевого баланса используют для целей
планирования. В этом случае задача ставится так: для планового периода
[Т0, T1] задается вектор у конечного потребления. Требуется определить вектор х валового выпуска.
Слайд 15Нужно решить задачу: сколько следует произвести продукции различных видов, чтобы
обеспечить заданный уровень конечного потребления? В этом случае необходимо решить
систему линейных уравнений с неизвестным вектором х при заданных матрице А и векторе у.
Слайд 16Ограничения модели
При этом нужно иметь в виду следующие особенности системы
1.
Все компоненты матрицы А и вектора у неотрицательны (определяется экономическим
смыслом А и у). Обычно говорят о неотрицательности самой матрицы А и вектора у : A>= 0, y>= 0.2. Все компоненты вектора х также должны быть неотрицательными: х >= 0.
Слайд 17Продуктивные модели Леонтьева
Определение. Матрица А>0 называется продуктивной, если для любого
вектора у>0 существует решение х > 0 уравнения X= Ах
+ у.В этом случае и модель Леонтьева, определяемая матрицей А, тоже называется продуктивной.
Т.О. модель Леонтьева продуктивна, если любой вектор у>=0 конечного потребления можно получить при подходящем валовом выпуске X >= 0.
Слайд 18Условия продуктивности
Теорема 1 (первый критерий продуктивности).
Если А >= 0
и для некоторого положительного вектора Y* уравнение имеет решение х>=0,
то матрица А продуктивна.
Слайд 19Условия продуктивности
Теорема 2 (второй критерий продуктивности).
Матрица A2>=0 продуктивна тогда
и только тогда, когда матрица (Е-А)-1 существует и неотрицательна.
Слайд 20Условия продуктивности
Теорема 3 (третий критерий продуктивности). Матрица А >= 0
продуктивна тогда и только тогда, когда сходится бесконечный ряд
Е +
А+А2 + А3... 
Слайд 21Правила проверки продуктивности
Если сумма элементов любого столбца неотрицательной матрицы А
меньше 1 , то А продуктивна.
Если в неотрицательной матрице
А сумма элементов любой строки меньше 1 , то матрица А продуктивна. 
Слайд 22Запас продуктивности
Пусть А >= 0 - продуктивная матрица. Запасом продуктивности
матрицы А назовем такое число α > 0, что все
матрицы λА, где 1 < λ < 1+α, продуктивны, а матрица (1+ α)А - не продуктивна.
Слайд 23Модель равновесных цен
Рассмотрим теперь балансовую модель, двойственную к модели
Леонтьева - равновесных цен. Пусть, А - матрица прямых затрат,
x = (x1 х2,..., хn) - вектор валового выпуска.
Слайд 24Обозначим через p=(p1,p2,рn) - вектор цен, i-я координата которого
равна цене единицы продукции i-й отрасли; тогда, первая отрасль
получит доход, равный р1х1, вторая – р2х2 и т.д.
Слайд 25Модель равновесных цен
Часть своего дохода эта отрасль потратит на закупку
продукции у других отраслей. Так, для выпуска единицы продукции ей
необходима продукция первой отрасли в объеме a11, второй отрасли в объеме а21, n-й отрасли в объеме аn, и т. д. На покупку этой продукции ею будет затрачена сумма, равная а11p1 +а21р2 + ••• + аn1pn.
Слайд 26Модель равновесных цен
Тогда для выпуска продукции в объеме x1 первой
отрасли необходимо потратить на закупку продукции других отраслей сумму, равную
x1*(а11p1 + а22р2 + ... + an1pn). Обозначим оставшуюся часть дохода, называемую добавленной стоимостью, через V1, (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).
Слайд 27Модель равновесных цен
Получим равенство:
X1P1 = X1(a11p1 + a21 P2 +
.. + an1 Рn) + V1. Разделив это равенство на
X1, получаемP1 = (a11P1 + a21 P2 + .. + an1 Рn) + V1
где V1 = P1/X1 норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).
Слайд 28Модель равновесных цен
Аналогично получим для остальных отраслей
P2 =(a12p1 + a22
P2 + .. + an2 Рn) + V2
…..
Pn =(a1np1 +
a2n P2 + .. + ann Рn) + VnНайденные равенства могут быть записаны в матричной форме : P=ATP+ V
где V = (V1, V2,..., Vn) - вектор норм добавленной стоимости.
Слайд 29Модель равновесных цен
Модель равновесных цен позволяет, зная величины норм добавленной
стоимости, прогнозировать цены на продукцию отраслей. Она также позволяет прогнозировать
изменение цен и инфляцию, являющиеся следствием изменения цены в одной из отраслей.
Слайд 30Метод наименьших квадратов
Метод наименьших квадратов (часто называемый МНК) обычно упоминается
в двух контекстах. Во-первых, использование в регрессионном анализе, как метода
построения моделей статистических данных. Во-вторых, МНК часто применяется просто как метод аппроксимации, без какой-либо привязки к статистике.
Слайд 31
Общий линейный метод наименьших квадратов
При аппроксимации методом наименьших квадратов аппроксимируемая
функция f задается набором N точек (xi , yi ). Аппроксимирующая функция
g строится, как линейная комбинация базисных функций Fj (количество функций M обычно меньше числа точек N)
Слайд 33При этом коэффициенты cj выбираются таким образом, чтобы минимизировать сумму
квадратов отклонений аппроксимирующей функции от заданных значений
