Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы математического анализа при исследовании СЭП
Содержание
- 1. Методы математического анализа при исследовании СЭП
- 2. 1.Элементарные функции Степенная Y=XnПоказательная Y=aXЛогарифмическая Y=logaXТригонометрические
- 3. 1.Предельные величины в экономике Теоретический анализ
- 4. Предельные величины в экономике Пусть q
- 5. Предельные величины в экономике Пример. Пусть C(q)
- 6. 2.Эластичность и ее свойстваДля исследования предельных величин
- 7. ЭластичностьОпределение. Эластичностью функции у = f(x) в
- 8. ЭластичностьЕсли ясно, в какой точке определяется эластичность
- 9. ЭластичностьТ.О. эластичность Еу - это коэффициент пропорциональности
- 10. Свойства эластичности1. Эластичность в точке х0 суммы
- 11. Свойства эластичности2. Эластичность произведения функций U =
- 12. Свойства эластичности3. Эластичность частного функций и =
- 13. Свойства эластичности4. Для функций у =f(x) и
- 14. Задания:Найти эластичность функции y=C – constНайти эластичность функции y=x+CНайти эластичность функции y=xa
- 15. Геометрический смысл эластичности.Геометрический смысл производной: f'(x0) -
- 16. Слайд 16
- 17. Если эластичность Y по X положительна, то
- 18. 3.Ценовая эластичность спроса. Пусть D = D(p)
- 19. Совершенно неэластичный спросТермин означает крайний случай, когда
- 20. Эластичность спросаЕсли имеется достаточный запас товара, то D
- 21. ВыводЕсли спрос эластичен, то изменение цены вызывает
- 22. Цена, предельные издержки и объем производстваПусть q
- 23. Цена, предельные издержки и объем производства1)Функции R(q),C(q)
- 24. Цена, предельные издержки и объем производстваПусть условия
- 25. Цена, предельные издержки и объем производстваВ экономической
- 26. 4. Задачи оптимального потребительского выбораПусть х -
- 27. Функцией полезности U(x,y) называется функция, задающая степень
- 28. Данная функция удовлетворяет следующим условиям: 1. Для
- 29. Теорема ДебреДля стандартных предпочтений потребителя всегда можно построить функцию полезности.
- 30. Основные виды функций полезности
- 31. Данное семейство функций полезности описывает предпочтения потребителя
- 32. Задание на самостоятельную подготовкуНайти и проанализировать другие
- 33. Общая постановка задачи состоит в поиске набора
- 34. Задача минимизации стоимости. Общая постановка задачи
- 35. Нахождение функций спроса.Определение. Пусть функция полезности U(x,y)
- 36. Функции спроса.Тогда x*, y* - функции от
- 37. Скачать презентанцию
1.Элементарные функции Степенная Y=XnПоказательная Y=aXЛогарифмическая Y=logaXТригонометрические Y=sinX;Обратные тригонометрические функции Y=arcsinX….Элементарными функциями называются такие, которые получаются из основных с помощью допустимых действий
Слайды и текст этой презентации
Слайд 1Методы математического анализа при исследовании СЭП
Понятие предельных величин в экономике.
Эластичность
и ее свойства
Слайд 2
1.Элементарные функции
Степенная Y=Xn
Показательная Y=aX
Логарифмическая Y=logaX
Тригонометрические Y=sinX;
Обратные тригонометрические функции Y=arcsinX….
Элементарными функциями
называются такие, которые получаются из основных с помощью допустимых действий
Слайд 3
1.Предельные величины в экономике
Теоретический анализ разнообразных явлений экономики использует ряд
предельных величин. Основными являются: предельные издержки, предельный доход, предельная производительность,
предельная полезность, предельная склонность к потреблению и т.д. Все эти величины самым тесным образом связаны с понятием производной. Рассмотрим предельные издержки.
Слайд 4
Предельные величины в экономике
Пусть q - количество произведенной продукции, C(q)
- издержки соответствующие данному выпуску. Обозначим предельные издержки МС, которые
определяются как дополнительные издержки, связанные с производством еще одной единицы продукции. Тогда MC= C(q+Δq)-C(q)Используя равенство ΔC ≈ dC, получим
МС =ΔС ≈ dC = C'(q) •Δ q = C'(q).
Поэтому МС ≈ C'(q).
Слайд 5Предельные величины в экономике
Пример.
Пусть C(q) = 1500q - 2q2
+ 0,002q3. Тогда дополнительные издержки, связанные с увеличением выпуска от
q до q + 1, составят ΔС = C(q + 1) - C(q), что приближенно равноC'(q) ≈ 1500 -4q + 0,006 q 2.
Слайд 62.Эластичность и ее свойства
Для исследования предельных величин используется понятие эластичности.
Понятие
эластичности было введено Аланом Маршаллом в связи с анализом функции
спроса. Это понятие является чисто математическим и может применяться при анализе любых дифференцируемых функций.
Слайд 7Эластичность
Определение.
Эластичностью функции у = f(x) в точке х0 называется
предел
Eyx(x0) = lim [(Δy/y] / [(Δx/x)]
ΔХ→0 Еyx (х0) - называют коэффициентом эластичности у по X.
![ЭластичностьОпределение. Эластичностью функции у = f(x) в точке х0 называется пределEyx(x0) = lim [(Δy/y] / [(Δx/x)]](/img/thumbs/1d8c4981f0a0633dc477138c572af988-800x.jpg "Методы математического анализа при исследовании СЭП ЭластичностьОпределение. Эластичностью функции у = f(x) в точке х0 называется пределEyx(x0)")
Слайд 8Эластичность
Если ясно, в какой точке определяется эластичность и какая переменная
является независимой, то могут опускаться отдельные символы. Часто используются сокращенные
обозначения Еy и Еyx .Из определения эластичности вытекает, что при достаточно малых Δх выполняется приближенное равенство
Δy/y : Δx/x ≈ Ey или
Δy/y ≈ Ey * Δx/x
Слайд 9Эластичность
Т.О. эластичность Еу - это коэффициент пропорциональности между относительными изменениями
величин у и х. Если, например, х увеличится на один
процент, то у увеличивается ≈ на Еy процентов.Ey ≈(x/y)*y ′
Слайд 10Свойства эластичности
1. Эластичность в точке х0 суммы y=y1+...+yn положительных функций
Yi=fi(X) (i= 1, 2, ..., n) удовлетворяет соотношению Emin
Emin(Emax) - это минимальная (максимальная) эластичность в точке x0 функций yt.
Слайд 11Свойства эластичности
2. Эластичность произведения функций U = U(х) и V
= V(x) в точке X0 равна сумме эластичностей функций и
и v в той же точке:Euv=Eu+Ev
Слайд 12Свойства эластичности
3. Эластичность частного функций и = и(х) и v
= v(x) в точке х0 (v(x0 ) ≠ 0) равна
разности эластичностей функций и и v в той же точке:Eu/v=Eu-Ev
Слайд 13Свойства эластичности
4. Для функций у =f(x) и х = g(t)
эластичность у по t в точке t0 удовлетворяет следующему равенству:
Yet(t0)=Eyx(g(t0))*Ext(t0)
Слайд 14Задания:
Найти эластичность функции y=C – const
Найти эластичность функции y=x+C
Найти эластичность
функции y=xa
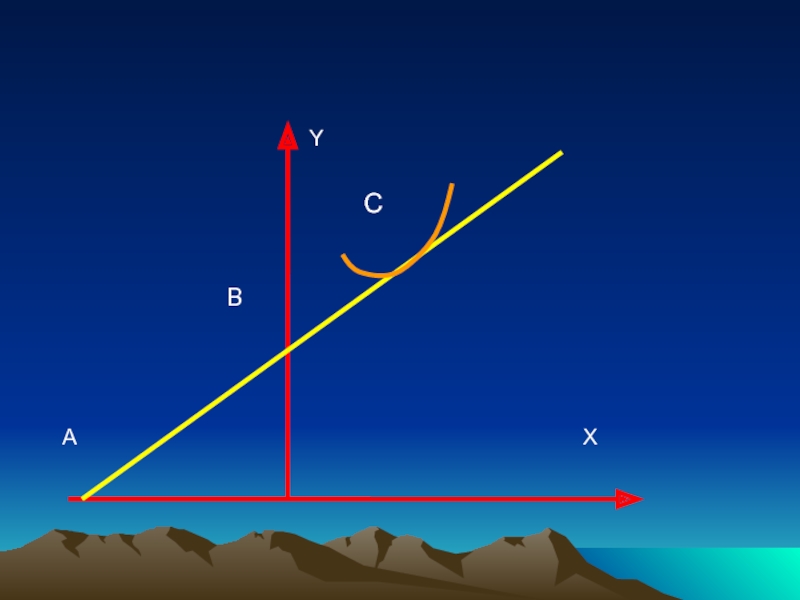
Слайд 15Геометрический смысл эластичности.
Геометрический смысл производной: f'(x0) - это тангенс угла
наклона касательной к графику функции у =f(x) в точке С(х0,
у0), у0 =f(x0). Геометрический смысл эластичности функции f(x) в точке x0 связан с разбиением данной касательной на отрезки точками А, В и С, где А(X0, 0) - точка пересечения касательной с осью Ох, B(0, уb) - точка пересечения касательной с осью Оу
Слайд 17Если эластичность Y по X положительна, то она совпадает с
отношением длин отрезков BC и АС
Eyx(x0)=BC/AC
Если эластичность Y по
X отрицательна , то выполняется следующее соотношениеEyx(x0)=- BC/AC
Слайд 183.Ценовая эластичность спроса.
Пусть D = D(p) - спрос (в
натуральных единицах) на некоторый товар при цене P. Так как
при увеличении цены спрос уменьшается, то эластичность спроса ED < 0. Спрос называется эластичным, если │ЕD│ > 1, и неэластичным, если │ED │< 1.
Слайд 19Совершенно неэластичный спрос
Термин означает крайний случай, когда изменение цены не
приводит ни к какому изменению спроса. В этом случае ED
= 0. В другом крайнем случае, когда самое малое снижение цены побуждает покупателя увеличивать покупки от нуля до предела своих возможностей, говорят, что спрос является совершенно эластичным. Можно считать, что для совершенно эластичного спроса │ED │= ∞.
Слайд 20Эластичность спроса
Если имеется достаточный запас товара, то D = D(p) –
то он характеризует количество проданного товара. В этом случае общая
выручка всех продавцовR =P*D.
Находим эластичность выручки по цене
ER=R'/R *P= ((D + PD')/PD)*P=
1+ (D'/D)*P=1+ED
Т.О., при эластичном спросе ER < 0, а при неэластичном спросе ER > 0.
Слайд 21Вывод
Если спрос эластичен, то изменение цены вызывает изменение общей выручки
в противоположном направлении. Если же спрос неэластичен, то изменение общей
выручки происходит в том же направлении, что и изменение цены.
Слайд 22Цена, предельные издержки и объем производства
Пусть q - выпуск продукции
(в натуральных единицах); R(q) -выручка от продаж; C(q) - издержки
производства, связанные с выпуском q единиц продукции. Тогда прибыльП(q)=R(q)-C(q)
Слайд 23Цена, предельные издержки и объем производства
1)Функции R(q),C(q) определены на полуинтервале
[0, +∞) и дифференцируемы при q> 0.
2) Тогда максимум прибыли
достигается в некоторой точке q* ≠ 0.
Слайд 24Цена, предельные издержки и объем производства
Пусть условия 1), 2) выполнены.
Тогда функция П(q) = R(q) -C(q) дифференцируема и имеет на
интервале (0, + ∞) максимум в точке q*≠ 0. По теореме Ферма П'(q*) = 0. Так какП'(q) = R' (q) -C'(q) то в точке q = q* имеем равенство
R' (q*) = C'(q*)
Слайд 25Цена, предельные издержки и объем производства
В экономической теории равенство объясняется
как правило, согласно которому фирма, максимизирующая свою прибыль, устанавливает объем
производства таким образом, чтобы предельная выручка была равна предельным издержкам.В случае, когда объем производства q не влияет на цену продукции р, имеем R(q) =pq, R' (q) =p.
Тогда p = C'(q*)
Слайд 264. Задачи оптимального потребительского выбора
Пусть х - количество единиц первого
продукта в наборе, у - количество единиц второго продукта в
наборе, p1 -цена единицы первого продукта, р2 -цена единицы второго продукта, U(x,y) - полезность набора (x,y)) выраженная числом, х*р1 + у*р2 -стоимость набора (х, у);I - количество средств, которое можно суммарно потратить на первый и второй продукты
Слайд 27Функцией полезности U(x,y) называется функция, задающая степень полезности набора товаров,
состоящего из х единиц товара Х и у единиц товара
У.
Слайд 28Данная функция удовлетворяет следующим условиям:
1. Для любых двух наборов
товаров X и Y , таких, что
выполняется2. Для любых двух наборов товаров X и Y , таких , что выполняется .
Слайд 29Теорема Дебре
Для стандартных предпочтений потребителя всегда можно построить функцию полезности.
Слайд 31Данное семейство функций полезности описывает предпочтения потребителя соответствующие полностью взаимозаменяемым
товарам, т. е. ситуации, когда уменьшение потребление, какого либо вида
товара может быть компенсировано потреблением дополнительных единиц любого другого товара.
Слайд 32Задание на самостоятельную подготовку
Найти и проанализировать другие виды функций полезности.
Функцию
полезности с полным дополнением благ (функция полезности Леонтьева)
Неоклассическую функцию
полезности (функция полезности Кобба-Дугласа)Функции безразличия.
Слайд 33Общая постановка задачи состоит в поиске набора (х,y) максимизирующего функцию
полезности и не превосходящего при этом по стоимости величины I.
U
(x,у) —>max P1 *Х+ P2У*≤I, х≥0, у ≥0
Слайд 34
Задача минимизации стоимости.
Общая постановка задачи состоит в поиске набора (X,Y)
минимальной стоимости, обеспечивающего заданную полезность Uзад.
I=P1x+P2y ? min, U(x,y)>=
Uзад,x>=0, y>=0.
Слайд 35Нахождение функций спроса.
Определение. Пусть функция полезности U(x,y) при любых положительных
Р1, Р2 и I имеет на множестве (Р1*Х+ Р2*Y)≤I, х≥0,
у ≥0) единственную точку глобального максимума (x*, y*).
Слайд 36Функции спроса.
Тогда x*, y* - функции от P1,P2,I.
X* = XD*
(P1,P2,I)
Y* = YD* (P1,P2,I)
Эти функции называются функциями спроса.
Доказано, что
U′ x(x,y) / U′y(x,y)=P1/P2P1*X+P2*Y=I
