«скалярную» меру качества – целевую функцию
Определяют набор независимых переменных и
формулируют условия,которые характеризуют их приемлемые значения (размерность задачи и ее
ограничения).
Решение оптимизационной задачи – это приемлемый набор значений
переменных, которому отвечает оптимальное значение целевой функции.
Под оптимальностью обычно понимают минимальность целевой функции.












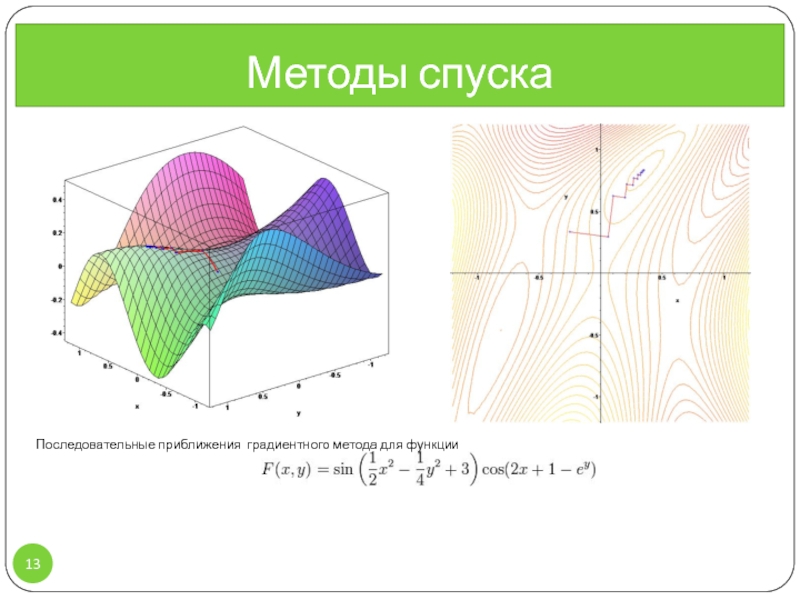
,[x,y]); > plot3d(z(x,y),x=-1.2..1.2,y=-1.2..1.2,axes=normal,numpoints=1000);p3d:=%: > contourplot(z(x,y),x=-1.2..1.2,y=-1.2..1.2, axes=normal, contours=30, numpoints=3000);cont:=%: restart:with(VectorCalculus):with(plots):with(plottools): z:=(x,y)->sin(1/2*x^2-1/4*y^2+3)*cos(2*x+1-exp(y)): > grad:=VectorCalculus[Gradient](z(x,y),[x,y]); > plot3d(z(x,y),x=-1.2..1.2,y=-1.2..1.2,axes=normal,numpoints=1000);p3d:=%: > contourplot(z(x,y),x=-1.2..1.2,y=-1.2..1.2, axes=normal, contours=30, numpoints=3000);cont:=%: > start:=[-1/4,1/3];ptf[0]:=Vector(start): > steps:=15; > for](/img/thumbs/1d01e7fd2ae0c14e06628260f2fc3280-800x.jpg)