Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Многогранники
Содержание
- 1. Многогранники
- 2. A1A2A3βB1B2B3BnBn-1Элементы призмы:1.Грань
- 3. Призма называется прямой, если……..Призма называется правильной, если……..Диагоналями призмы называются отрезки, соединяющие..A1A2A3An-1B1B2B3BnBn-1Диагональными сечениями призмы называются сечения, проходящие…An
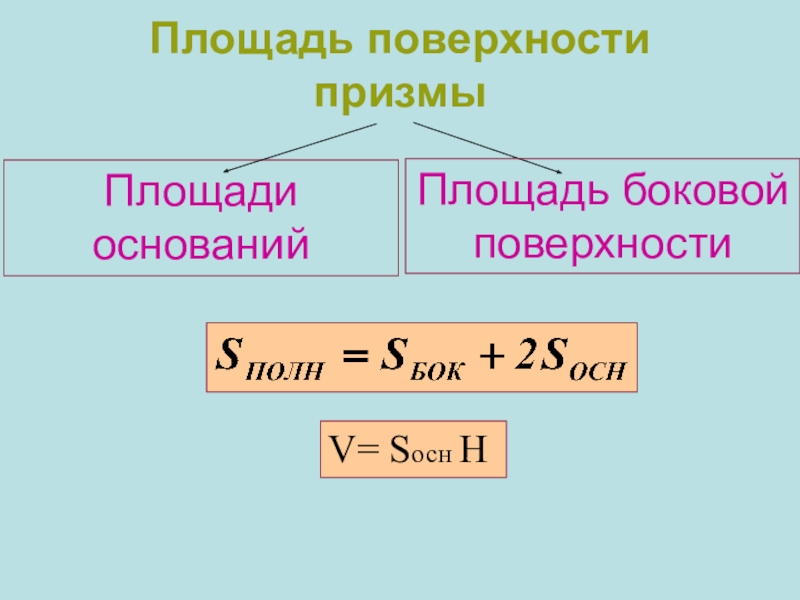
- 4. Площадь поверхности призмыПлощади основанийПлощадь боковой поверхностиV= Sосн H
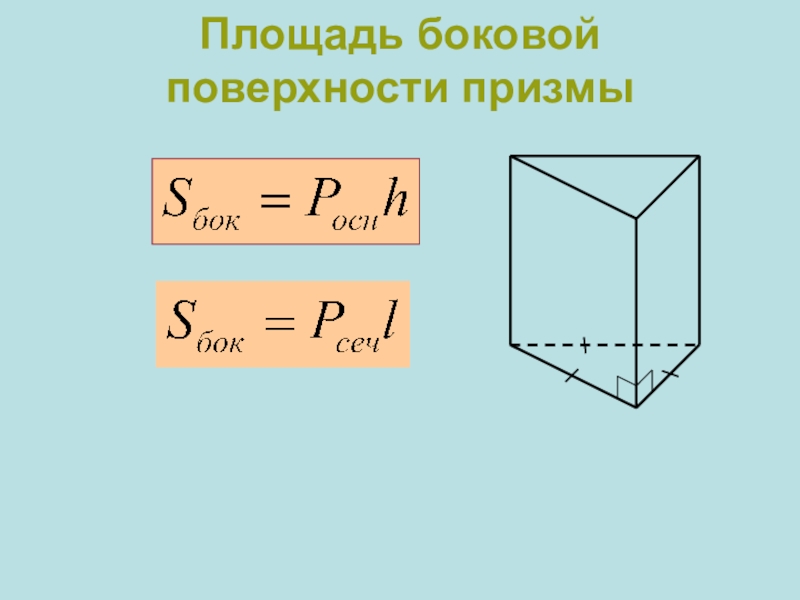
- 5. Площадь боковой поверхности призмы
- 6. Параллелепипед - это призма, основание которой является ПАРАЛЛЕЛОГРАМОМ.Параллелепипед называется прямым, если…Параллелепипед называется прямоугольным, если…
- 7. ПИРАМИДА (n-угольная) - это многогранник,
- 8. ПРАВИЛЬНАЯ
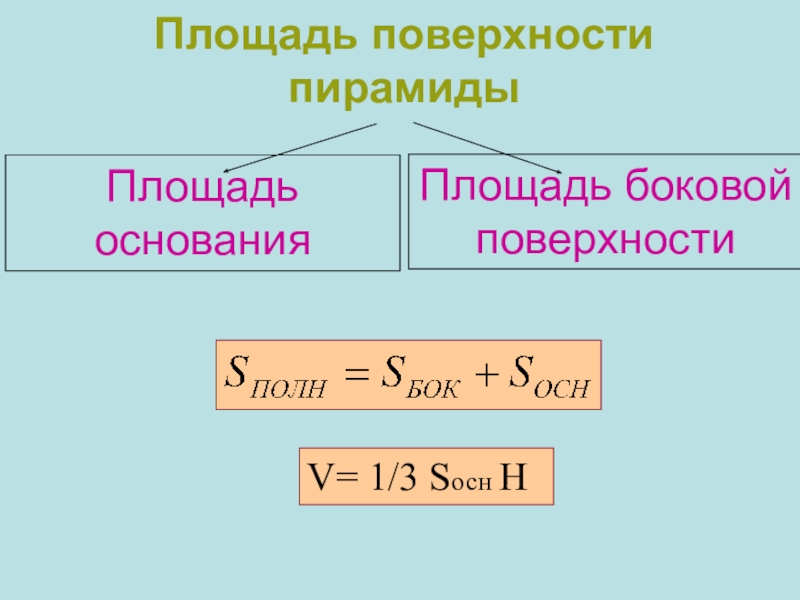
- 9. Площадь поверхности пирамидыПлощадь основанияПлощадь боковой поверхностиV= 1/3 Sосн H
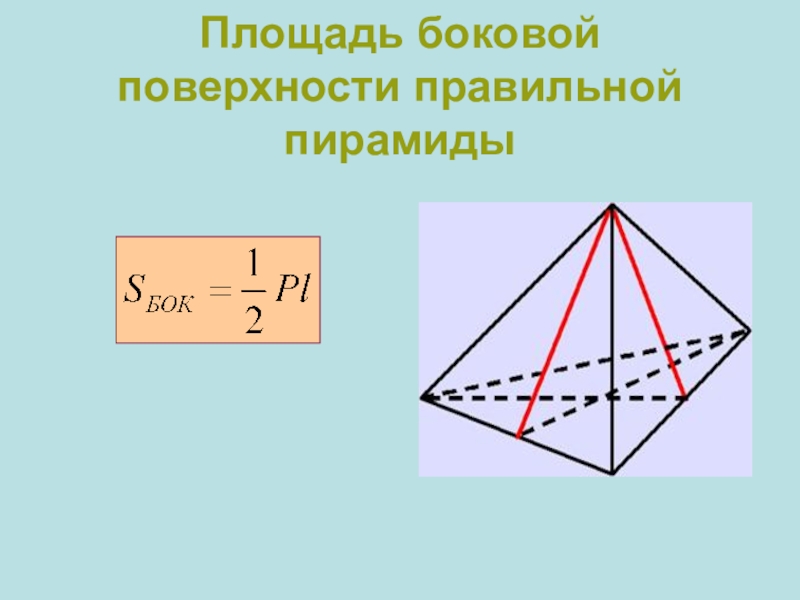
- 10. Площадь боковой поверхности правильной пирамиды
- 11. Усеченная пирамида – многогранник, основаниями которого являются
- 12. Площадь поверхности усеченной пирамидыПлощадь полной поверхности(Сумма площадей
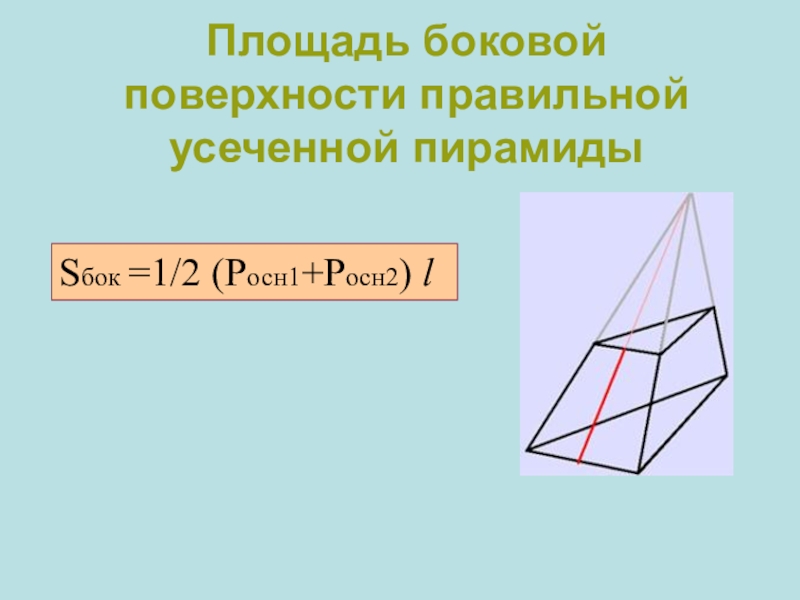
- 13. Площадь боковой поверхности правильной усеченной пирамиды Sбок =1/2 (Росн1+Росн2) l
- 14. Тела вращения
- 15. Слайд 15
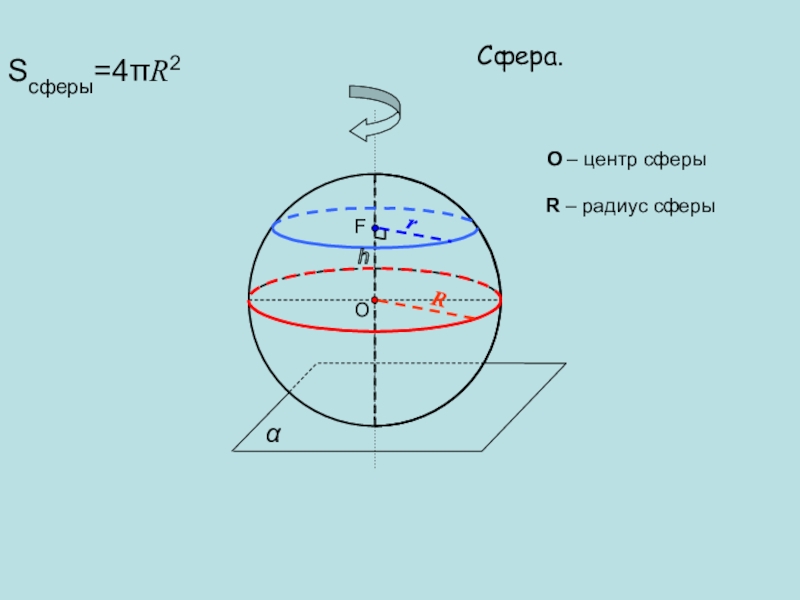
- 16. Сфера.OO – центр сферыRR – радиус сферыFhrSсферы=4R2
- 17. Слайд 17
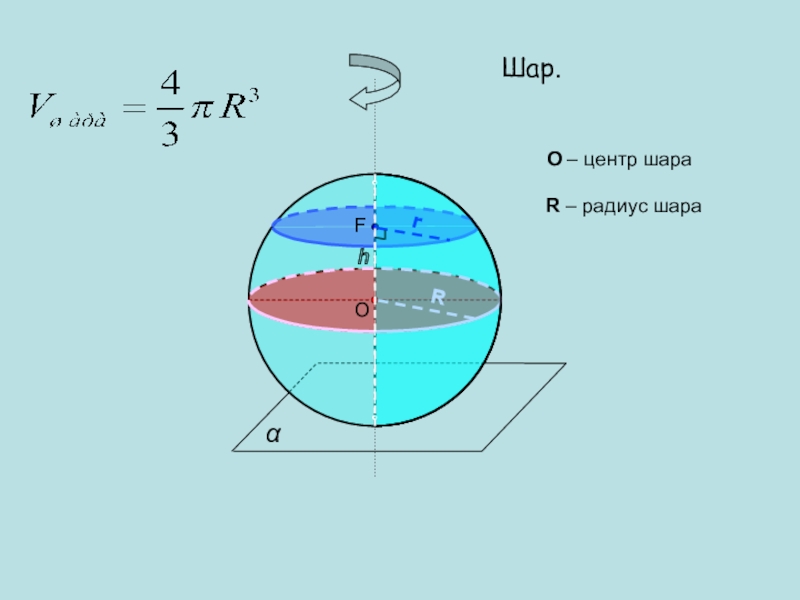
- 18. Шар.OO – центр шараRR – радиус шараFhr
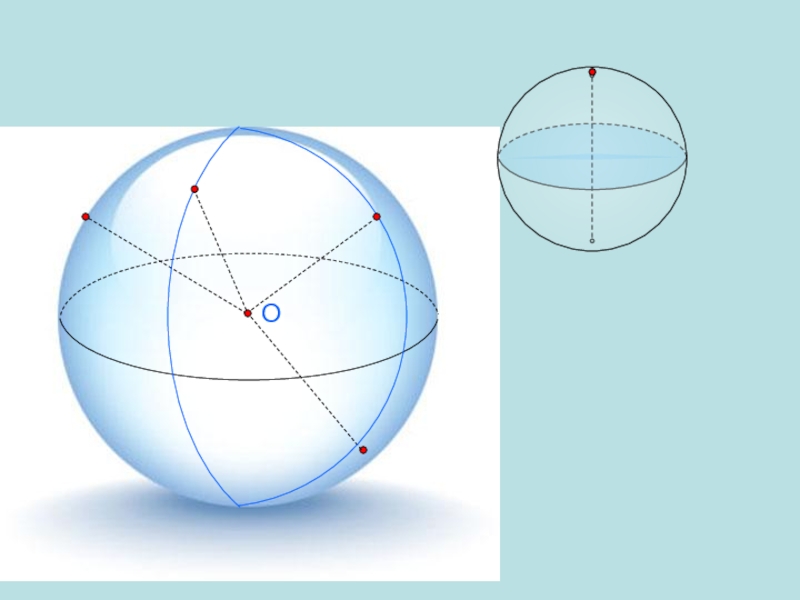
- 19. O
- 20. Слайд 20
- 21. Цилиндр.H – высота цилиндраR – радиус основанияL
- 22. Формулы для вычисления площади поверхности и объема цилиндра:RHxx[0;H]H0xSбок.=2RHSосн.=R2Sполн.=2Sосн.+Sбок.=2R2+2RHxH0xVцил.=R2H
- 23. Конус.H – высота конусаR – радиус основанияL
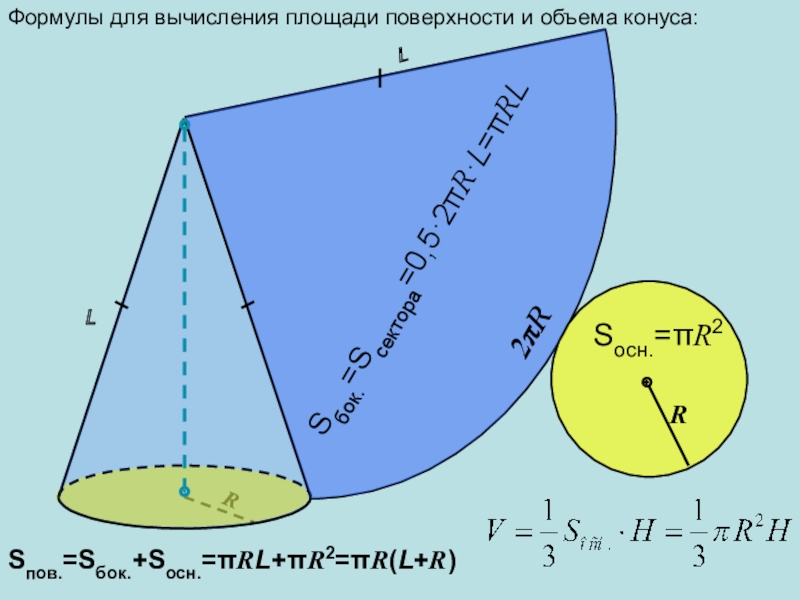
- 24. Формулы для вычисления площади поверхности и объема конуса:RRL2RLSбок.=Sсектора=0,5·2R·L=RLSосн.=R2Sпов.=Sбок.+Sосн.=RL+R2=R(L+R)
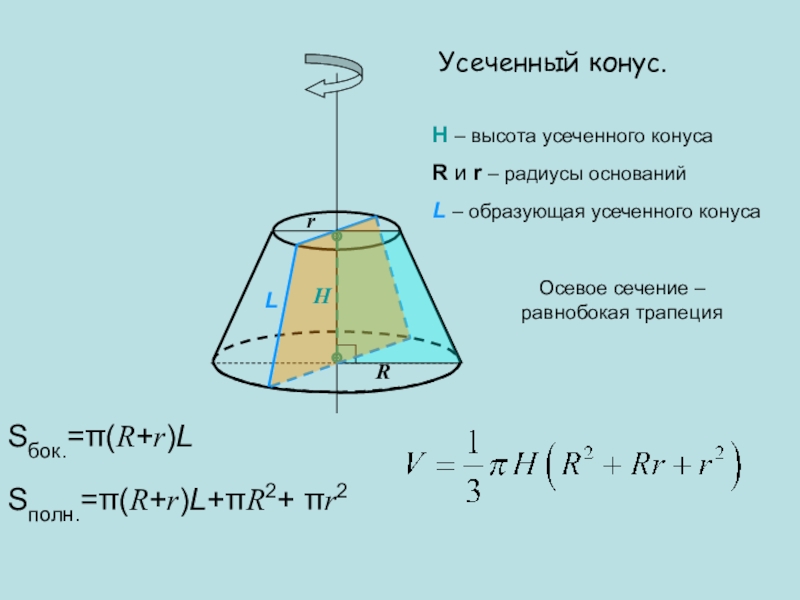
- 25. Усеченный конус.H – высота усеченного конусаR и
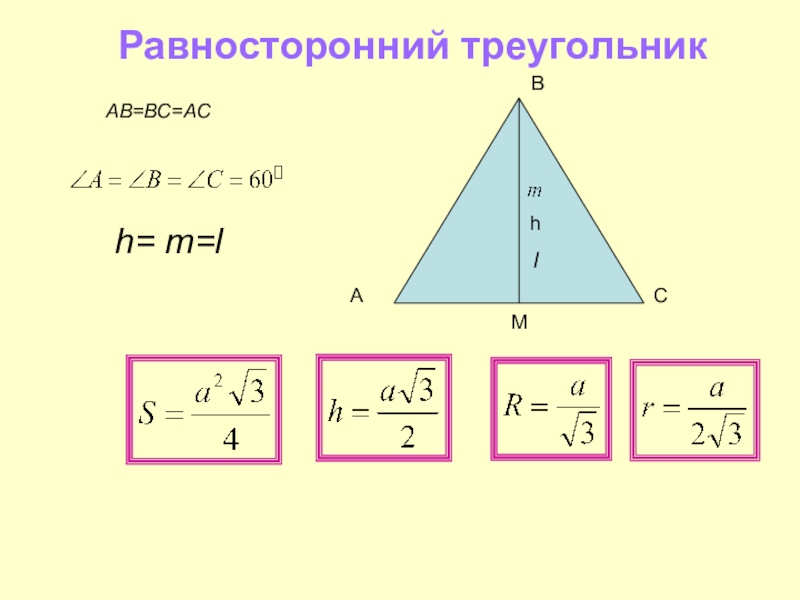
- 26. Равносторонний треугольникСhВMh= m=llАВ=ВС=AС А
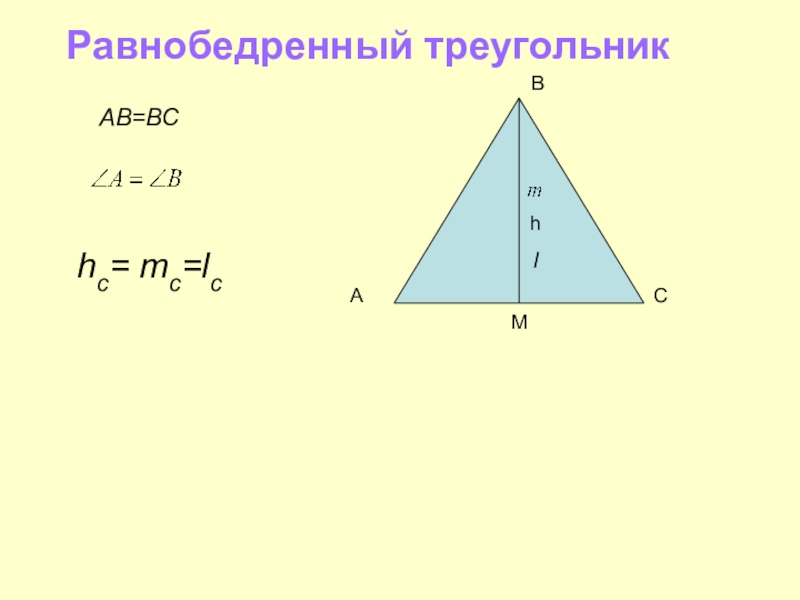
- 27. Равнобедренный треугольникСhВMhс= mс=lсlАВ=ВС А
- 28. Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
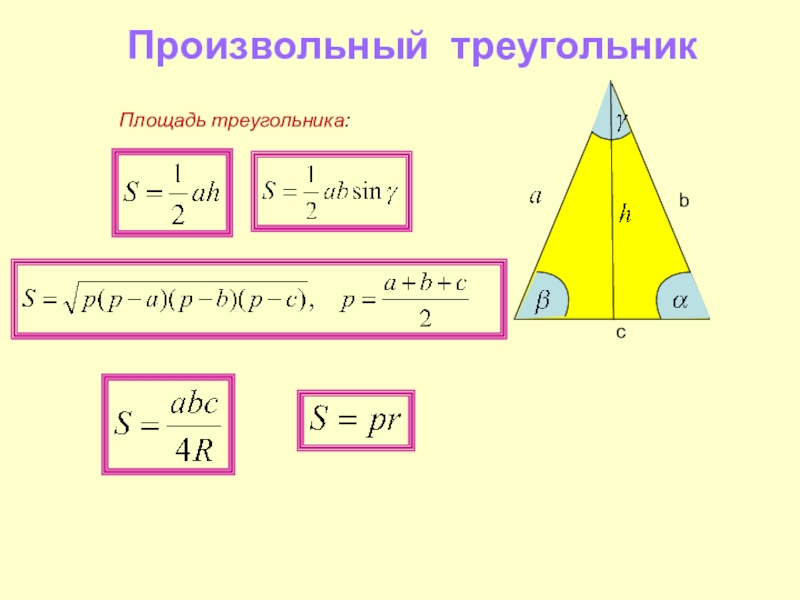
- 29. Произвольный треугольникcbПлощадь треугольника:
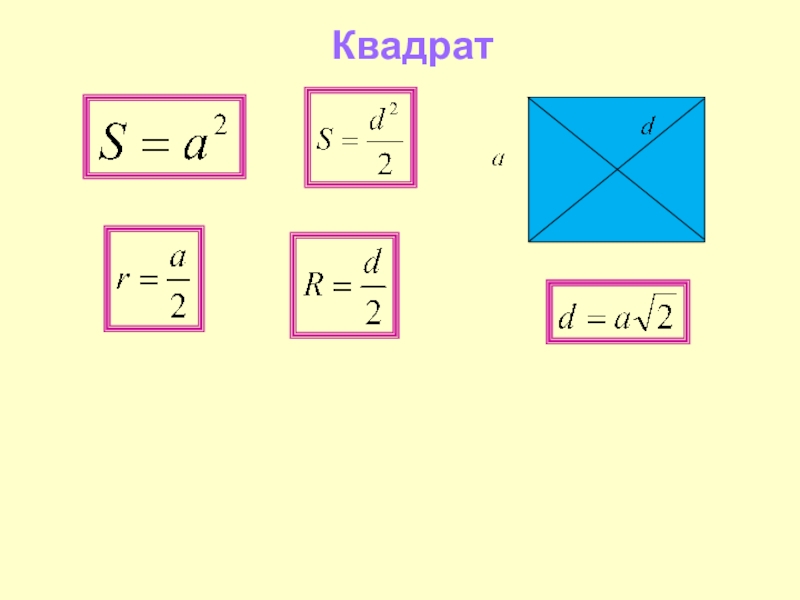
- 30. Квадрат
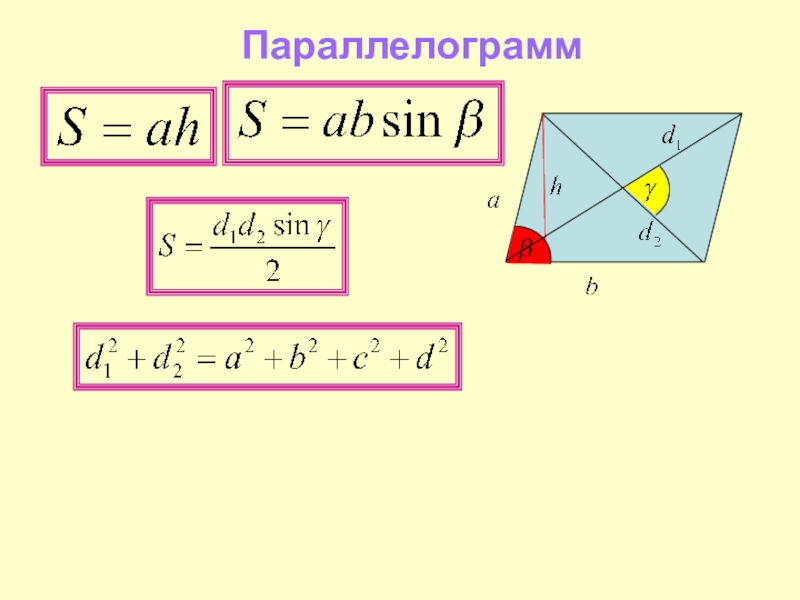
- 31. Параллелограмм
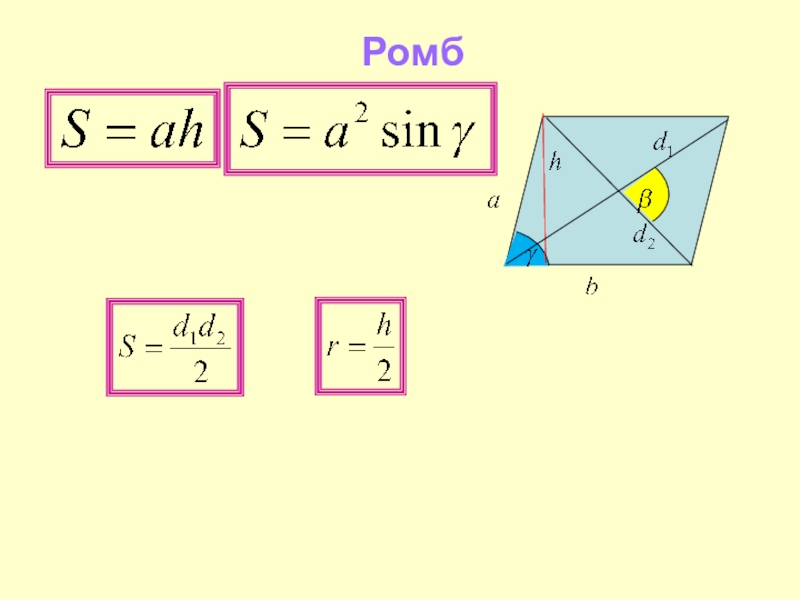
- 32. Ромб
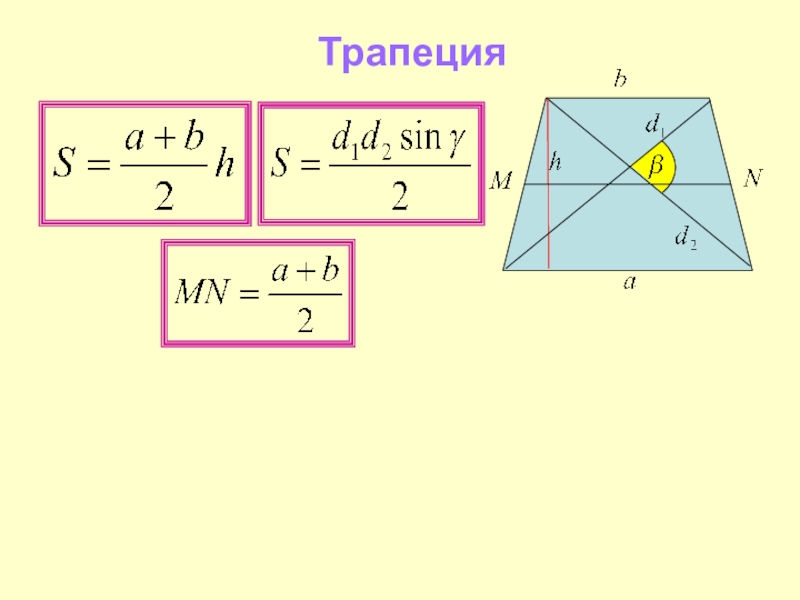
- 33. Трапеция
- 34. Скачать презентанцию
A1A2A3βB1B2B3BnBn-1Элементы призмы:1.Грань
Слайды и текст этой презентации
Слайд 2A1
A2
A3
β
B1
B2
B3
Bn
Bn-1
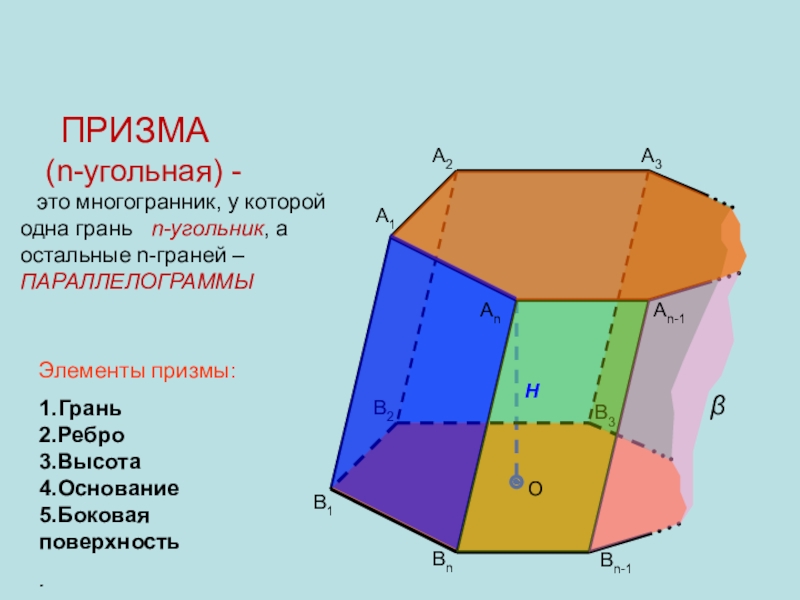
Элементы призмы:
1.Грань
2.Ребро 3.Высота
4.Основание
5.Боковая поверхность
.
An
An-1
H
O
ПРИЗМА
(n-угольная) -
это многогранник, у которой одна грань n-угольник, а остальные n-граней –ПАРАЛЛЕЛОГРАММЫ
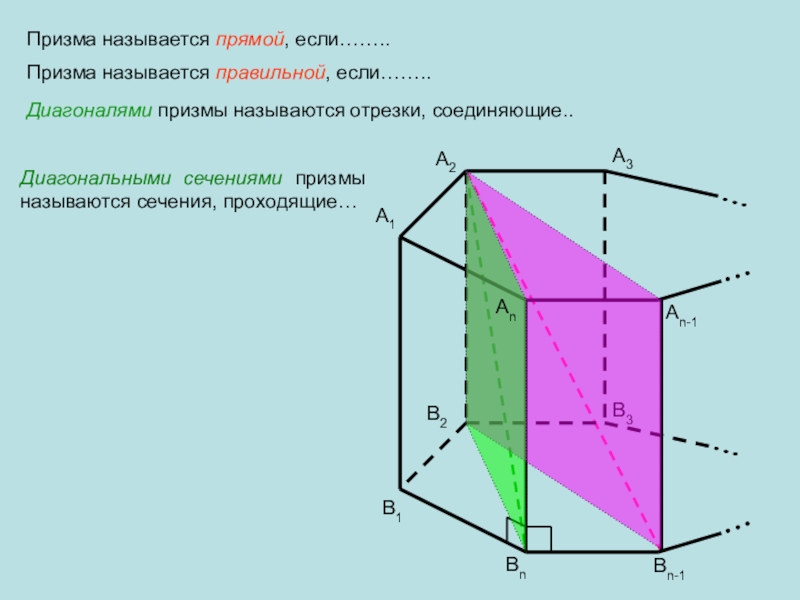
Слайд 3Призма называется прямой, если……..
Призма называется правильной, если……..
Диагоналями призмы называются отрезки,
соединяющие..
A1
A2
A3
An-1
B1
B2
B3
Bn
Bn-1
Диагональными сечениями призмы называются сечения, проходящие…
An
Слайд 6Параллелепипед - это призма, основание которой является ПАРАЛЛЕЛОГРАМОМ.
Параллелепипед называется прямым,
если…
Параллелепипед называется прямоугольным, если…
Слайд 7ПИРАМИДА
(n-угольная) -
это многогранник, у которой одна
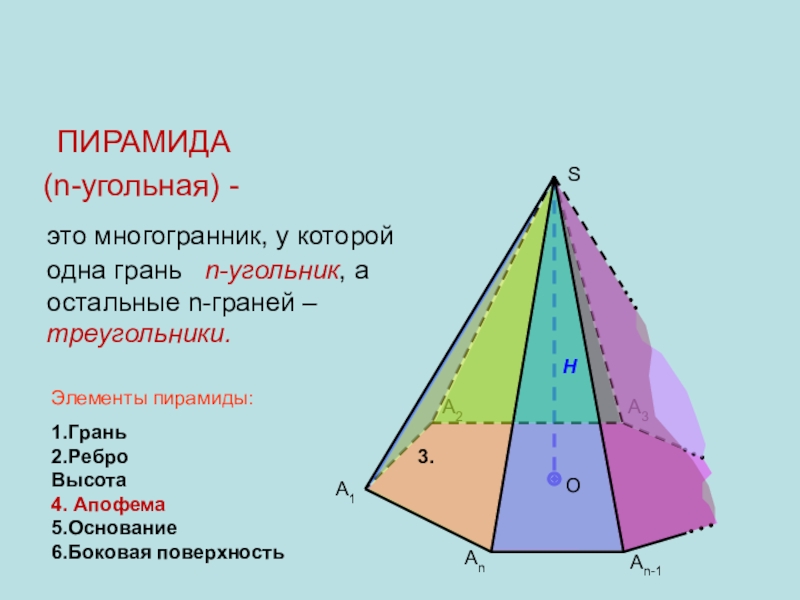
грань n-угольник, а остальные n-граней –треугольники.
A1
A2
A3
An
An-1
S
H
O
Элементы пирамиды:
1.Грань
2.Ребро 3.Высота 4. Апофема5.Основание
6.Боковая поверхность
Слайд 8ПРАВИЛЬНАЯ
ПИРАМИДА (n-угольная)
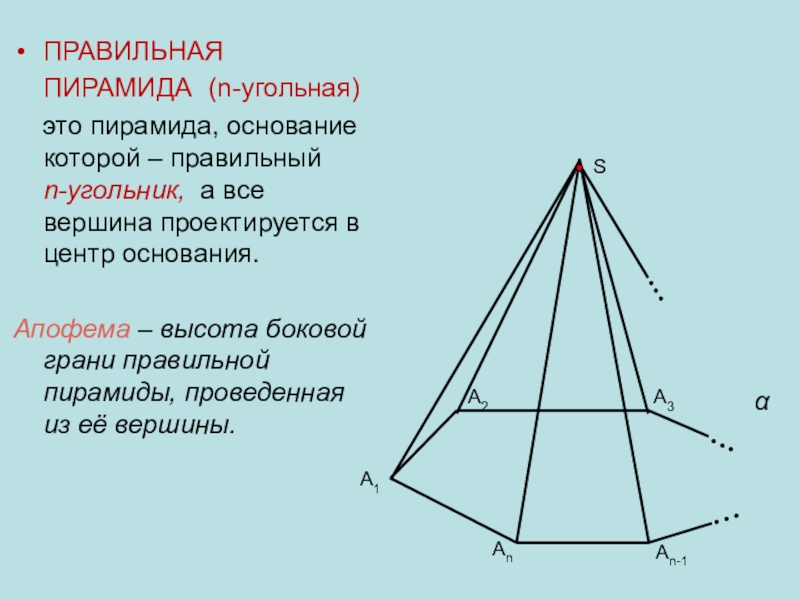
это пирамида, основание которой – правильный
n-угольник, а все вершина проектируется в центр основания.Апофема – высота боковой грани правильной пирамиды, проведенная из её вершины.
A1
A2
A3
An
An-1
S
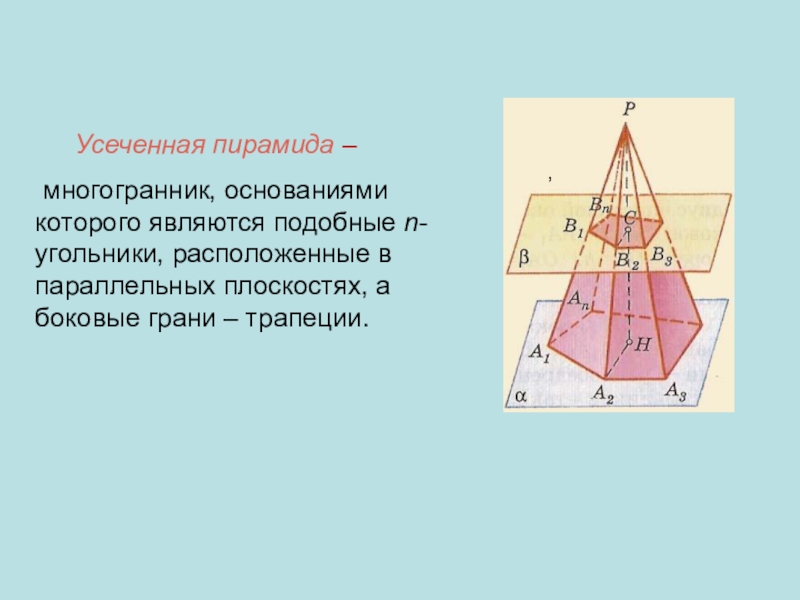
Слайд 11 Усеченная пирамида –
многогранник, основаниями которого являются подобные n-угольники, расположенные
в параллельных плоскостях, а боковые грани – трапеции.
,
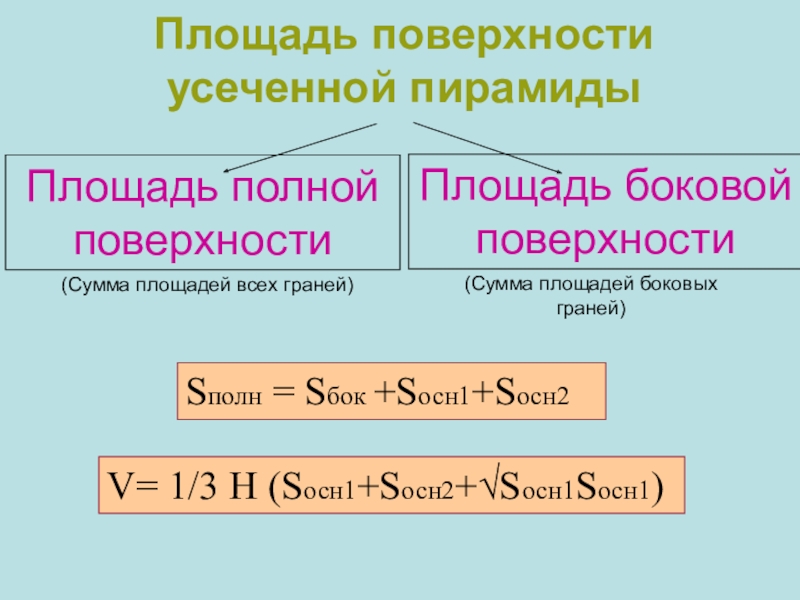
Слайд 12Площадь поверхности усеченной пирамиды
Площадь полной поверхности
(Сумма площадей всех граней)
(Сумма площадей
боковых граней)
Площадь боковой поверхности
Sполн = Sбок +Sосн1+Sосн2
V= 1/3 H (Sосн1+Sосн2+√Sосн1Sосн1)
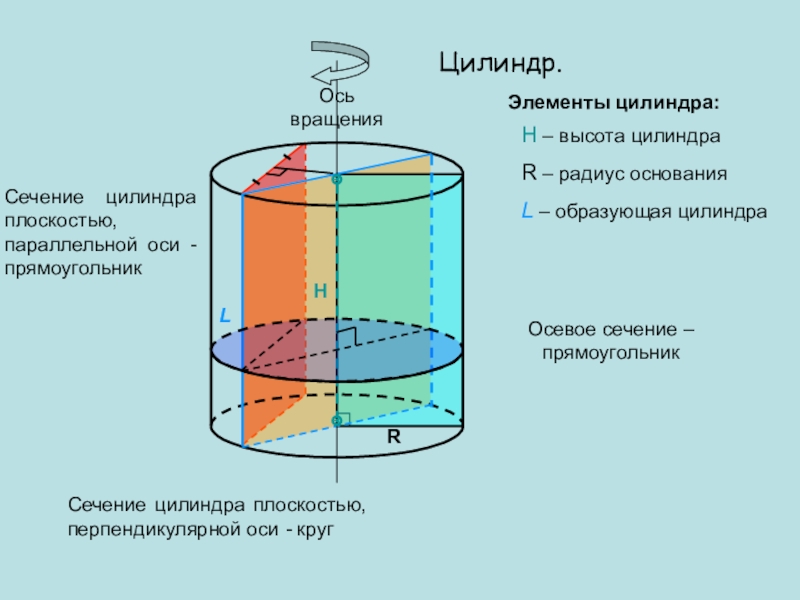
Слайд 21Цилиндр.
H – высота цилиндра
R – радиус основания
L – образующая цилиндра
H
R
L
Осевое
сечение – прямоугольник
Элементы цилиндра:
Сечение цилиндра плоскостью, параллельной оси - прямоугольник
Ось
вращенияСечение цилиндра плоскостью, перпендикулярной оси - круг
Слайд 22Формулы для вычисления площади поверхности и объема цилиндра:
R
H
x
x[0;H]
H
0
x
Sбок.=2RH
Sосн.=R2
Sполн.=2Sосн.+Sбок.=2R2+2RH
x
H
0
x
Vцил.=R2H
![Формулы для вычисления площади поверхности и объема цилиндра:RHxx[0;H]H0xSбок.=2RHSосн.=R2Sполн.=2Sосн.+Sбок.=2R2+2RHxH0xVцил.=R2H](/img/tmb/7/643979/90ba93d05fcef3eb7b5a55a4e94dfe11-800x.jpg "Многогранники Формулы для вычисления площади поверхности и объема цилиндра:RHxx[0;H]H0xSбок.=2RHSосн.=R2Sполн.=2Sосн.+Sбок.=2R2+2RHxH0xVцил.=R2H")
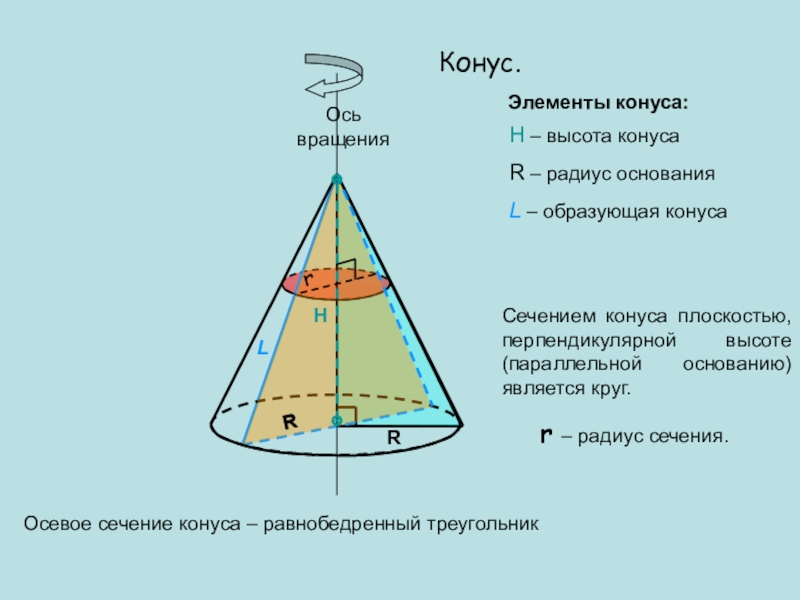
Слайд 23Конус.
H – высота конуса
R – радиус основания
L – образующая конуса
H
R
L
Осевое
сечение конуса – равнобедренный треугольник
r
Сечением конуса плоскостью, перпендикулярной высоте (параллельной
основанию) является круг.r – радиус сечения.
Элементы конуса:
Ось вращения
R
Слайд 24Формулы для вычисления площади поверхности и объема конуса:
R
R
L
2R
L
Sбок.=Sсектора=0,5·2R·L=RL
Sосн.=R2
Sпов.=Sбок.+Sосн.=RL+R2=R(L+R)
Слайд 25Усеченный конус.
H – высота усеченного конуса
R и r – радиусы
оснований
L – образующая усеченного конуса
R
L
Осевое сечение – равнобокая трапеция
H
r
Sбок.=(R+r)L
Sполн.=(R+r)L+R2+ r2
Слайд 28Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов:
