Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества. Операции над множествами
Содержание
- 1. Множества. Операции над множествами
- 2. «Множество есть многое, мыслимое нами как единое»основатель
- 3. Примеры множеств из окружающего мираНапример, множество дней
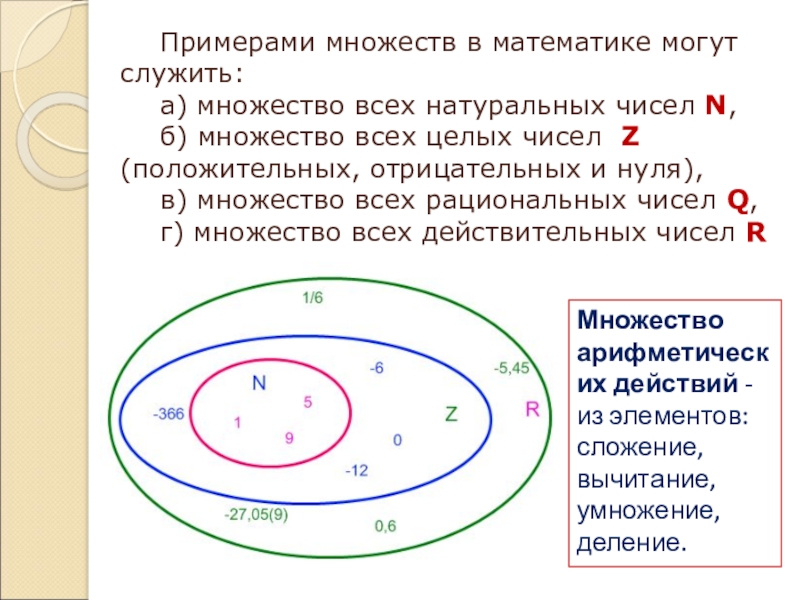
- 4. Примерами множеств в математике могут служить:а) множество
- 5. Примерами множеств в геометрии могут служить: а) множество видов треугольников,б) множество многоугольников
- 6. Пересечением двух множеств А и В называется
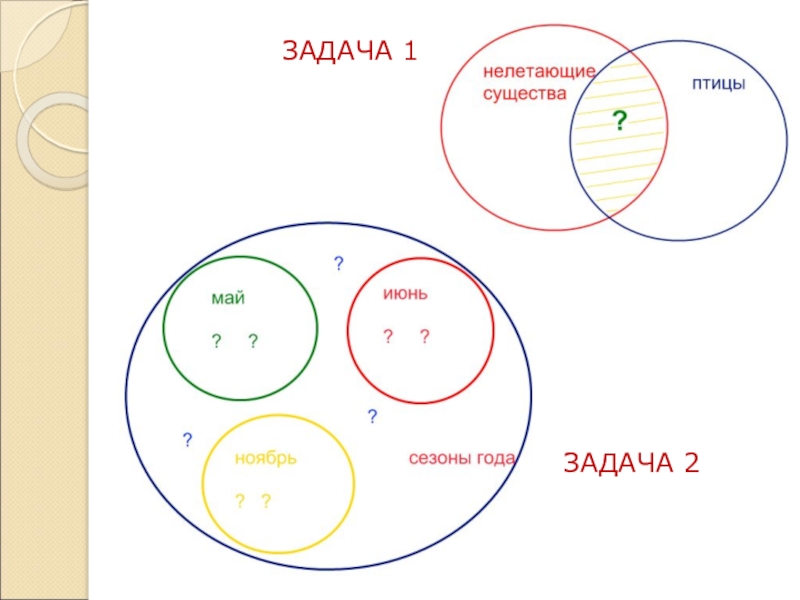
- 7. АЗАДАЧА 1ЗАДАЧА 2
- 8. Объединением двух множеств А и В называется
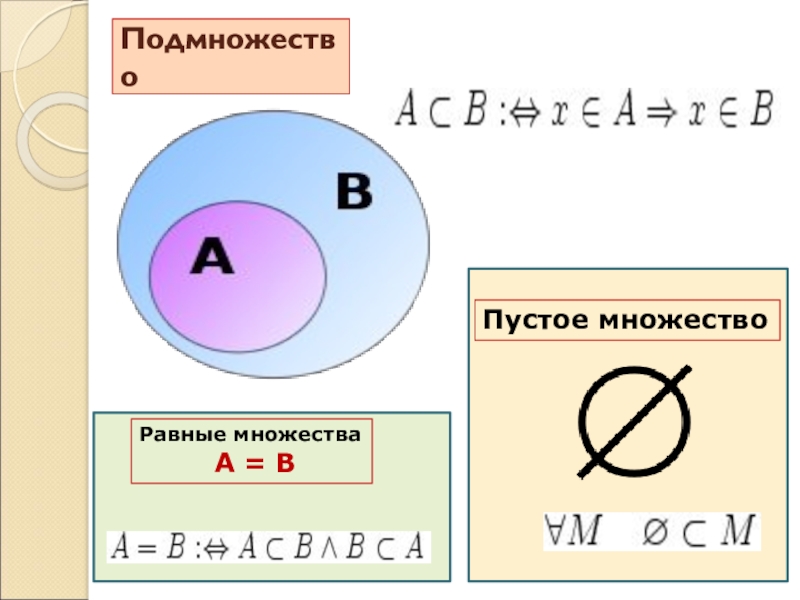
- 9. Подмножество
- 10. А={0,1,2,3,4,5,6,7,8,9} № 1Какое множество задано путем перечисления
- 11. РешениеВ четвёртом пенале должны лежать предметы, которые уже
- 12. № 5Изобразите с помощью кругов Эйлера пересечение
- 13. Решение: Обозначим через x число людей, являющихся
- 14. Домашнее задание:В киоске около школы продается мороженое
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2«Множество есть многое, мыслимое нами как единое»
основатель теории множеств –
Георг Кантор
множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв.Слайд 3Примеры множеств из окружающего мира
Например, множество дней недели состоит из
элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев –
из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.Слайд 4Примерами множеств в математике могут служить:
а) множество всех натуральных чисел
N,
б) множество всех целых чисел Z (положительных, отрицательных и нуля),
в)
множество всех рациональных чисел Q,г) множество всех действительных чисел R
Множество арифметических действий - из элементов: сложение, вычитание, умножение, деление.
Слайд 5Примерами множеств в геометрии могут служить:
а) множество видов треугольников,
б) множество
многоугольников
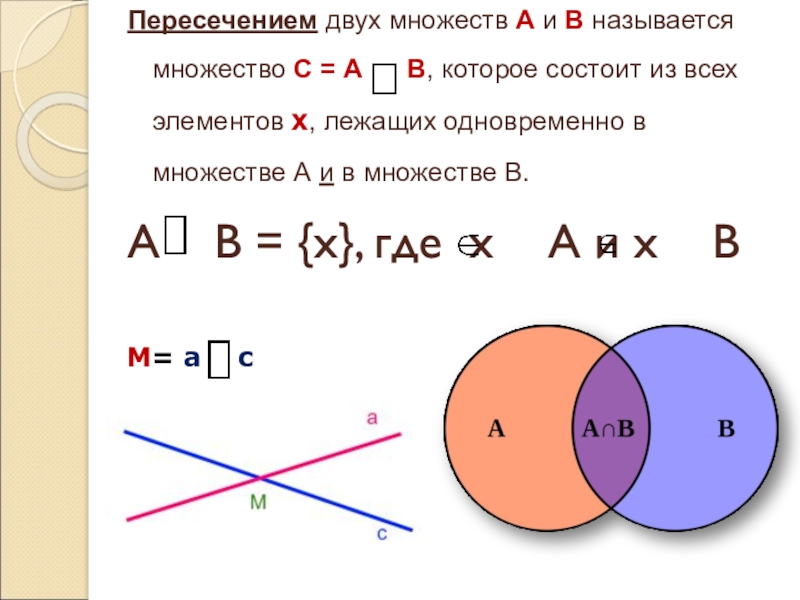
Слайд 6Пересечением двух множеств А и В называется множество С =
А В, которое состоит из всех элементов х,
лежащих одновременно в множестве А и в множестве В.А В = {х}, где х А и х В
М= а с
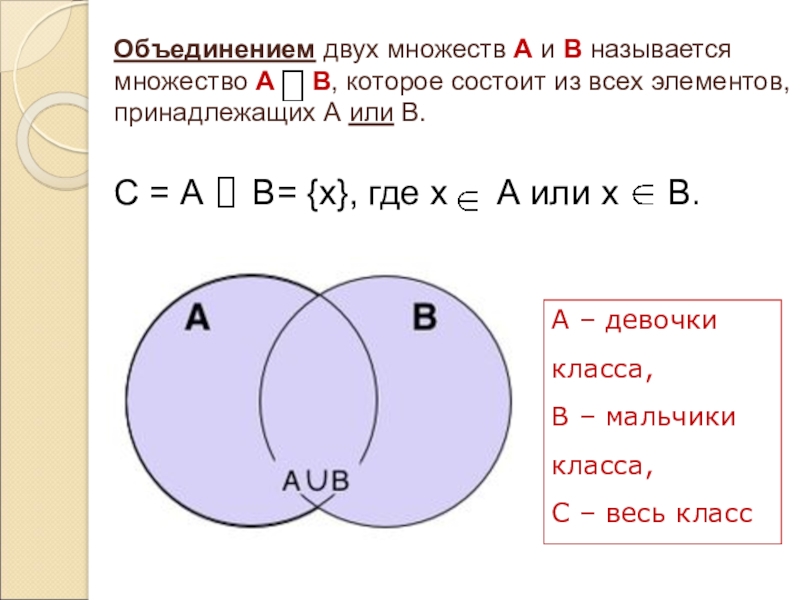
Слайд 8Объединением двух множеств А и В называется множество А
В, которое состоит из всех элементов, принадлежащих А или
В.С = А В= {х}, где х А или х В.
А – девочки класса,
В – мальчики класса,
С – весь класс
Слайд 10А={0,1,2,3,4,5,6,7,8,9}
№ 1
Какое множество задано путем перечисления данных элементов?
№ 2
Задайте
множество крокодилов, летящих в небе.
Даны множества
А = {3,
5, 0, 11, 12, 19},В = {2, 4, 8, 12, 18,0}. Найдите множества AUВ,
А В
№ 3
В={А,Е,И,О,У,Э,Ю,Я}
Слайд 11Решение
В четвёртом пенале должны лежать предметы, которые уже встречаются в первых трех
пеналах, но только по одному разу. Это синяя ручка, оранжевый карандаш и красный
ластик.Ответ
Синяя ручка, оранжевый карандаш, красный ластик.
Задача
В первом пенале лежат лиловая ручка, зелёный карандаш и красный ластик; во втором — синяя ручка, зелёный карандаш и жёлтый ластик; в третьем — лиловая ручка, оранжевый карандаш и жёлтый ластик. Содержимое этих пеналов характеризуется такой закономерностью: в каждых двух из них ровно одна пара предметов совпадает и по цвету, и по назначению. Что должно лежать в четвёртом пенале, чтобы эта закономерность сохранилась?
Подсказка
Подумайте, может ли в четвёртом пенале лежать лиловая ручка.
Слайд 12№ 5
Изобразите с помощью кругов Эйлера пересечение множеств
K и
L, если:
а) K L
б) L
Kв) K = L
г) K L =
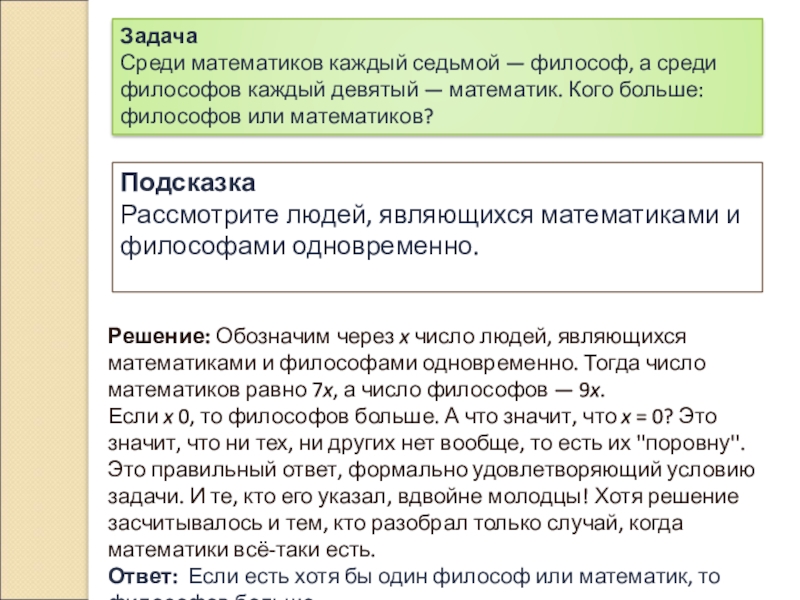
Слайд 13Решение: Обозначим через x число людей, являющихся математиками и философами
одновременно. Тогда число математиков равно 7x, а число философов — 9x.
Если
x 0, то философов больше. А что значит, что x = 0? Это значит, что ни тех, ни других нет вообще, то есть их ''поровну''. Это правильный ответ, формально удовлетворяющий условию задачи. И те, кто его указал, вдвойне молодцы! Хотя решение засчитывалось и тем, кто разобрал только случай, когда математики всё-таки есть. Ответ: Если есть хотя бы один философ или математик, то философов больше.
Задача
Среди математиков каждый седьмой — философ, а среди философов каждый девятый — математик. Кого больше: философов или математиков?
Подсказка
Рассмотрите людей, являющихся математиками и философами одновременно.
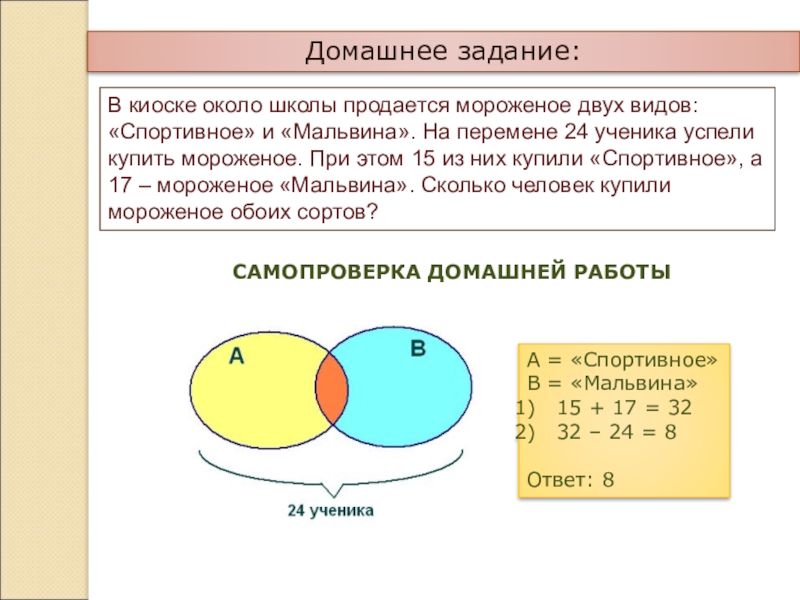
Слайд 14Домашнее задание:
В киоске около школы продается мороженое двух видов: «Спортивное»
и «Мальвина». На перемене 24 ученика успели купить мороженое. При
этом 15 из них купили «Спортивное», а 17 – мороженое «Мальвина». Сколько человек купили мороженое обоих сортов?САМОПРОВЕРКА ДОМАШНЕЙ РАБОТЫ