Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модель – это материальный или мысленно представленный объект, который в
Содержание
- 1. Модель – это материальный или мысленно представленный объект, который в
- 2. Модель – это материальный или мысленно представленный
- 3. Модель – это материальный или мысленно представленный
- 4. Модель – это материальный или мысленно представленный
- 5. Модель – это материальный или мысленно представленный
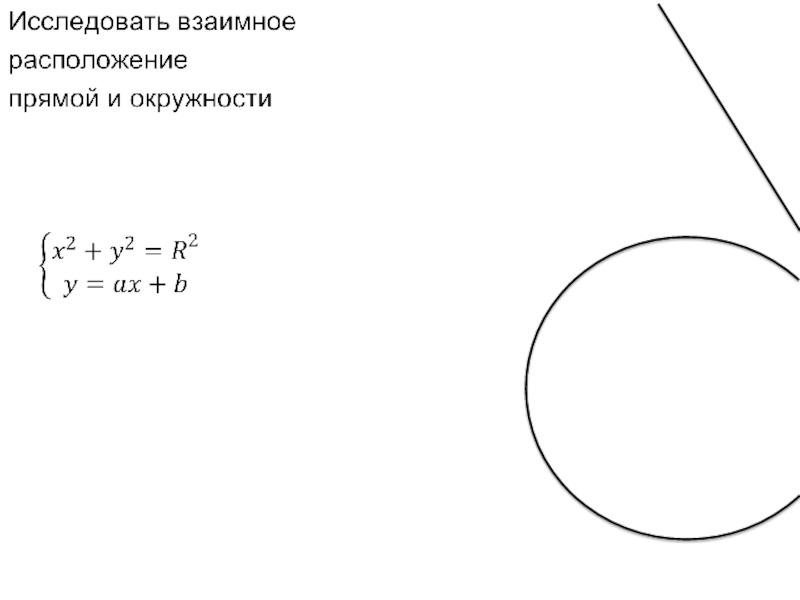
- 6. Исследовать взаимноерасположение прямой и окружности
- 7. Слайд 7
- 8. Сама постановка вопроса о математическом моделировании какого-либо
- 9. Определить начальную скорость револьверной пули
- 10. Определить начальную скорость револьверной пули Для этого
- 11. Эти трансформации описываются цепочкой равенств Здесь mv2/2
- 12. Эти трансформации описываются цепочкой равенств Здесь mv2/2
- 13. Это, на первый взгляд, разумное рассуждение на
- 14. Скачать презентанцию
Модель – это материальный или мысленно представленный объект, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства.Моделирование - это исследование какого либо объекта или системы объектов путем построения
Слайды и текст этой презентации
Слайд 2Модель – это материальный или мысленно представленный объект, который в
процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного
исследования типичные свойства.Моделирование - это исследование какого либо объекта или системы объектов путем построения и изучения их моделей.
Слайд 3Модель – это материальный или мысленно представленный объект, который в
процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного
исследования типичные свойства.Моделирование - это исследование какого либо объекта или системы объектов путем построения и изучения их моделей.
Особую роль в науке играют математические модели. При построении математической модели, изучаемого объекта или явления выделяют те его особенности, черты и детали, которые с одной стороны содержат более или менее полную информацию об объекте, а с другой допускают математическую формализацию.
Слайд 4Модель – это материальный или мысленно представленный объект, который в
процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного
исследования типичные свойства.Моделирование - это исследование какого либо объекта или системы объектов путем построения и изучения их моделей.
Особую роль в науке играют математические модели. При построении математической модели, изучаемого объекта или явления выделяют те его особенности, черты и детали, которые с одной стороны содержат более или менее полную информацию об объекте, а с другой допускают математическую формализацию.
Математическая формализация означает, что особенностям и деталям объекта можно поставить в соответствие подходящие адекватные математические понятия: числа, функции, матрицы и так далее. Тогда связи и отношения, обнаруженные и предполагаемые в изучаемом объекте между отдельными его деталями и составными частями можно записать с помощью математических отношений: равенств, неравенств, уравнений.
Слайд 5Модель – это материальный или мысленно представленный объект, который в
процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного
исследования типичные свойства.Моделирование - это исследование какого либо объекта или системы объектов путем построения и изучения их моделей.
Особую роль в науке играют математические модели. При построении математической модели, изучаемого объекта или явления выделяют те его особенности, черты и детали, которые с одной стороны содержат более или менее полную информацию об объекте, а с другой допускают математическую формализацию.
Математическая формализация означает, что особенностям и деталям объекта можно поставить в соответствие подходящие адекватные математические понятия: числа, функции, матрицы и так далее. Тогда связи и отношения, обнаруженные и предполагаемые в изучаемом объекте между отдельными его деталями и составными частями можно записать с помощью математических отношений: равенств, неравенств, уравнений.
В результате получается математическое описание изучаемого процесса или явление, то есть его математическая модель.
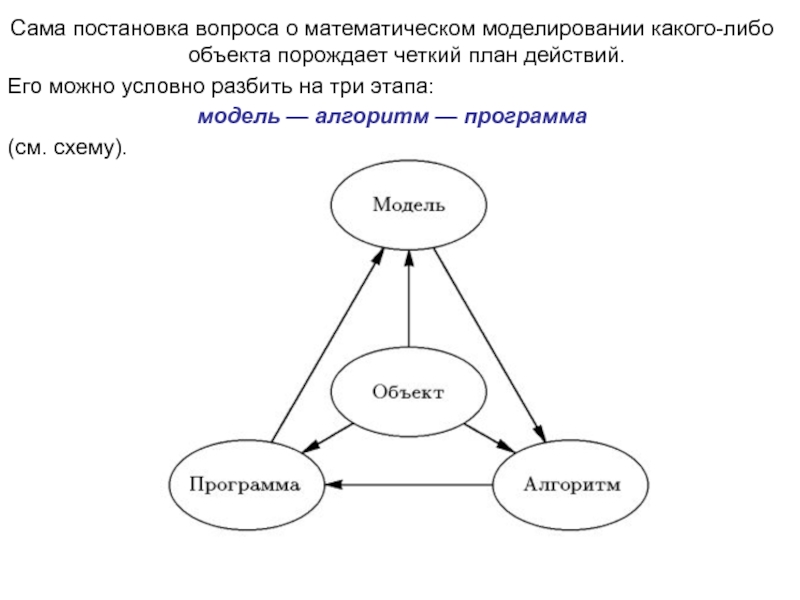
Слайд 8Сама постановка вопроса о математическом моделировании какого-либо объекта порождает четкий
план действий.
Его можно условно разбить на три этапа:
модель —
алгоритм — программа (см. схему).
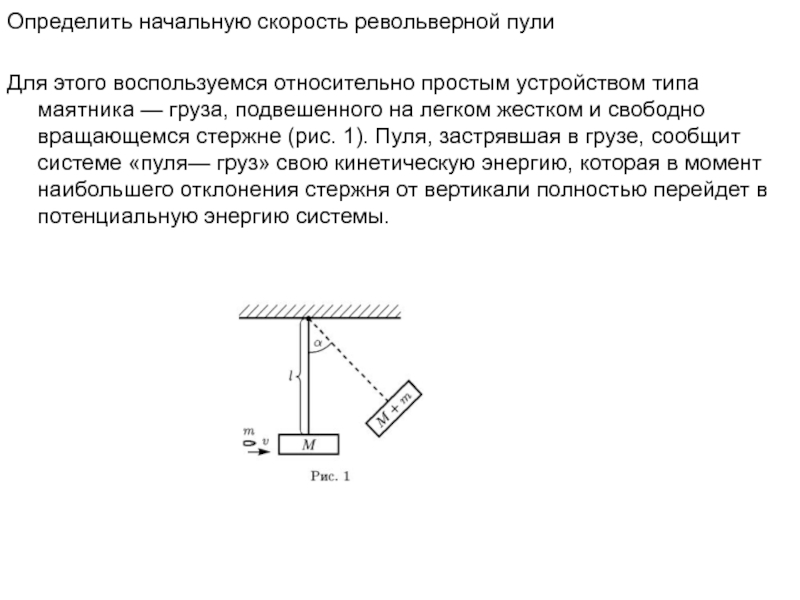
Слайд 10Определить начальную скорость револьверной пули
Для этого воспользуемся относительно простым
устройством типа маятника — груза, подвешенного на легком жестком и
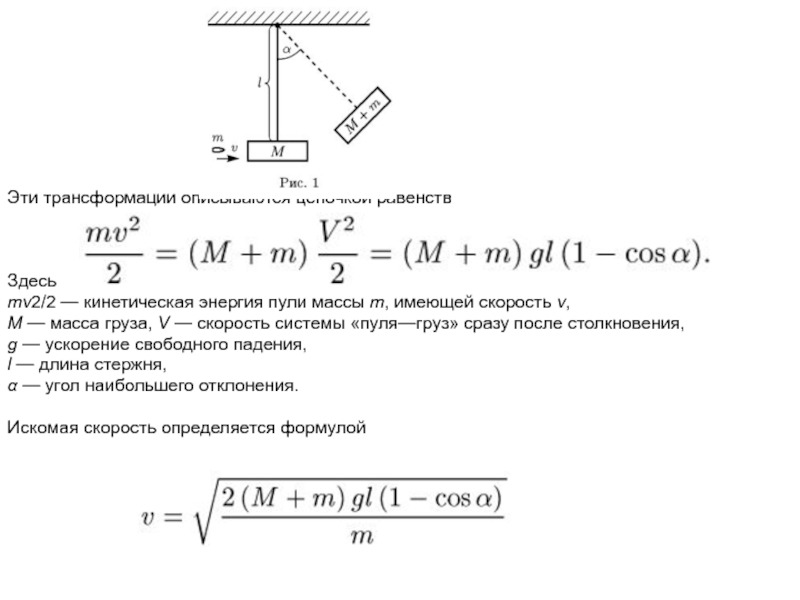
свободно вращающемся стержне (рис. 1). Пуля, застрявшая в грузе, сообщит системе «пуля— груз» свою кинетическую энергию, которая в момент наибольшего отклонения стержня от вертикали полностью перейдет в потенциальную энергию системы.Слайд 11
Эти трансформации описываются цепочкой равенств
Здесь
mv2/2 — кинетическая энергия
пули массы m, имеющей скорость v,
М — масса груза,
V — скорость системы «пуля—груз» сразу после столкновения, g — ускорение свободного падения,
l — длина стержня,
α — угол наибольшего отклонения.
Слайд 12
Эти трансформации описываются цепочкой равенств
Здесь
mv2/2 — кинетическая энергия
пули массы m, имеющей скорость v,
М — масса груза,
V — скорость системы «пуля—груз» сразу после столкновения, g — ускорение свободного падения,
l — длина стержня,
α — угол наибольшего отклонения.
Искомая скорость определяется формулой
Слайд 13Это, на первый взгляд, разумное рассуждение на самом деле неверно.
Процессы, происходящие при «слипании» пули и маятника, уже не являются
чисто механическими. Поэтому примененный для вычисления величины V закон сохранения механической энергии несправедлив: сохраняется полная, а не механическая энергия системы. Он дает лишь нижнюю границу для оценки скорости пули (для правильного решения этой простой задачи надо воспользоваться также законом сохранения импульса).