Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели представления знаний
Содержание
- 1. Модели представления знаний
- 2. Классификация по степени использования различных видов знаний
- 3. 1. Если в программной системе используются только
- 4. 2. Если в программной системе используются главным
- 5. 3. Если в программной системе в той
- 6. Классификация по виду ответа при решении задач
- 7. 2.Процедурный ответ; решая задачу, система может создать
- 8. Приведем примеры ответов разных уровней, используя модельный
- 9. На уровне 0 мы предъявляем последовательность, а
- 10. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙВ логических моделях знания
- 11. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙР — множество синтаксических
- 12. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙПростейшей логической моделью является
- 13. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙЛогика высказываний оперирует логическими
- 14. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ^ конъюнкция (логическое умножение);v дизъюнкция (логическое сложение);→ импликация (если - то);↔ эквивалентность.
- 15. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
- 16. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙИсчисление высказываний позволяет формализовать
- 17. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ В логике высказываний
- 18. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙРассмотрим ставший классическим пример
- 19. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙОднако эта формула не
- 20. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙЧтобы осуществить этот примитивный
- 21. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙОчевидно, что свойство конкретного
- 22. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ«Под предикатом будем понимать
- 23. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙНапример, если P и
- 24. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙВ логике предикатов факты
- 25. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙАргументы могут быть атомами
- 26. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙВыше приведенные примеры высказываний
- 27. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙПредикат с арностью n
- 28. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙПредикат "компьютер(память, клавиатура, процессор,
- 29. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙПредикат с арностью n
- 30. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
- 31. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙПеременные, находящиеся в сфере
- 32. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙК недостаткам логики предикатов
- 33. ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙневозможность применения в качестве
- 34. Лекция 4Фреймовая модель представления знаний
- 35. Фреймовая модельФреймовая модель представления знаний основана на
- 36. Фреймовая модельВ психологии и философии известно понятие
- 37. Фреймовая модельПРИМЕР Объект "мяч" представляет собой кожаный
- 38. Фреймовая модельФрейм имеет имя, служащее для идентификации
- 39. Фреймовая модельНапример, слот с именем возраст может
- 40. Фреймовая модельВ слоте может содержаться не одно,
- 41. Фреймовая модельСовокупность данных предметной области может быть
- 42. Фреймовая модельФреймы обладают способностью наследовать значения характеристик
- 43. Фреймовая модельСуществуют 2 типа фреймов – прототипы
- 44. Фреймовая модельНад фреймами можно совершать некоторые теоретико-множественные
- 45. Фреймовая модельПри пересечении фреймов в результирующем фрейме
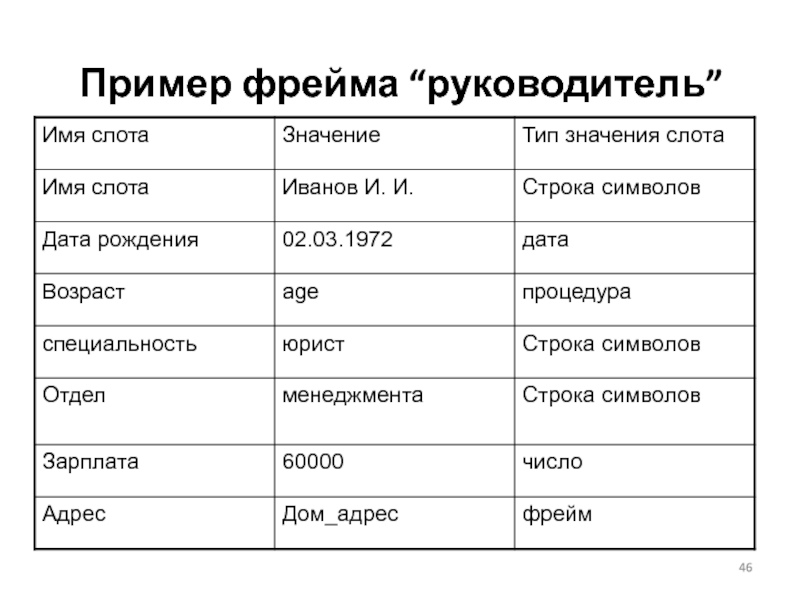
- 46. Пример фрейма “руководитель”
- 47. Структура данных фрейма Имя фрейма. Оно служит
- 48. Структура данных фреймаИмя слота. Оно должно быть
- 49. Структура данных фреймаУказатели наследования. Они показывают, какую
- 50. Структура данных фреймаU (Unique) — значение слота
- 51. Структура данных фреймаУказатель типа данных. Он показывает
- 52. Структура данных фреймаДемоны. Демоном называется процедура, автоматически
- 53. Структура данных фреймаДемон с условием IF-NEEDED запускается,
- 54. Структура данных фреймаПрисоединенная процедура запускается по сообщению,
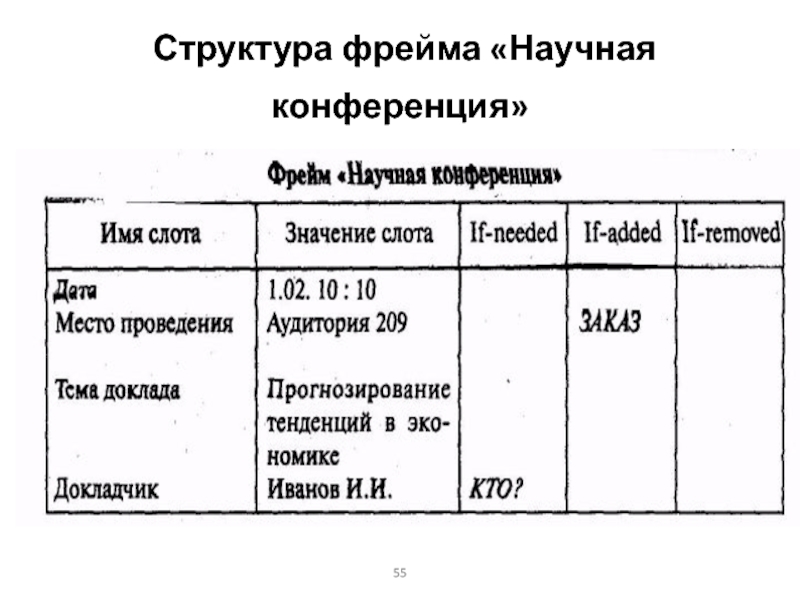
- 55. Структура фрейма «Научная конференция»
- 56. Структура фрейма «Научная конференция»Демон ЗАКАЗ — это
- 57. Структура фрейма «Научная конференция»Демон КТО? автоматически запускается
- 58. Слайд 58
- 59. Слайд 59
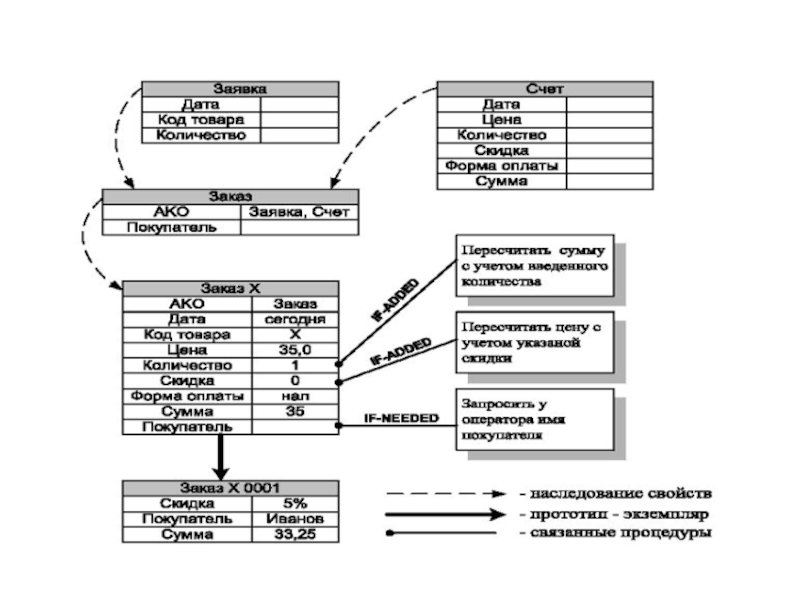
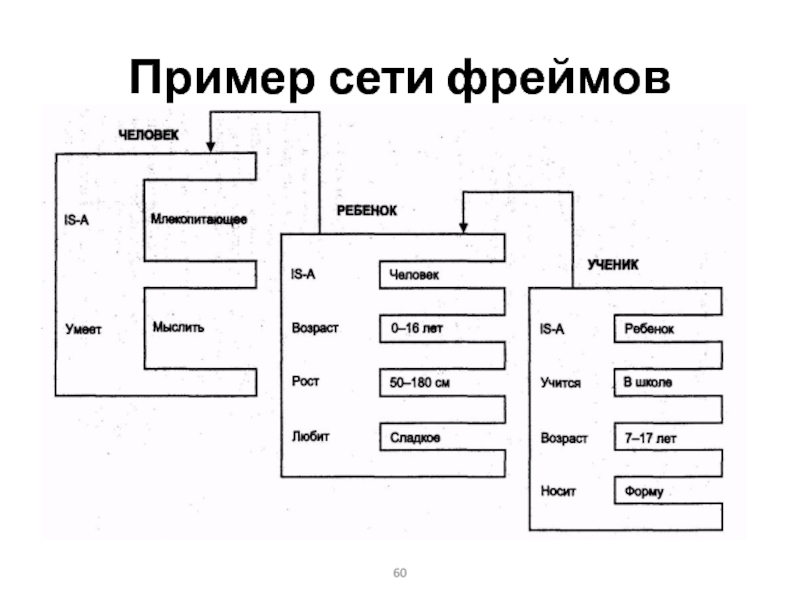
- 60. Пример сети фреймов
- 61. Пример сети фреймов Понятие УЧЕНИК наследует свойства
- 62. Пример сети фреймов Понятие УЧЕНИК наследует свойства
- 63. Фреймовая модель Модель фрейма является достаточно универсальной,
- 64. Фреймовая модель Пример. Фрейм-структурами являются понятия "заем",
- 65. Реализация фреймовой модели представления знаний на примере
- 66. Цель решения: определить, кому принадлежитрыба? При этом
- 67. 9.Норвежец живет в первом доме.10.Тот, кто держит
- 68. Если трактовать условие (4) как «зеленый домстоит
- 69. Попробуем представить предметную областьзадачи с помощью набора
- 70. На рис. 1 представлены фреймовые диаграммы классов
- 71. Слайд 71
- 72. Слайд 72
- 73. Другая часть информации может быть заложена вмодель
- 74. Сложнее обстоит дело с условиями типа «тот,
- 75. Фреймовая модель очень удобна с точки зрения
- 76. На рис. 2 представлена диаграмма классов, реализующих
- 77. Слайд 77
- 78. Вся предметная область разбита на пять уровней:1)
- 79. Программа действует методом проб и ошибок. На
- 80. Если позиция белого дома уже определена, и
- 81. На следующем уровне генерируется перестановка людей. После
- 82. зицию желтого дома и, обнаружив, что дом
- 83. На рис. 3 показана работа программы в
- 84. Слайд 84
- 85. Слайд 85
- 86. Фреймовая модель Основные преимущества фреймов как модели
- 87. Фреймовая модель Теория фреймов послужила толчком к
- 88. Фреймовая модель Теория фреймов послужила толчком к
- 89. Представление знаний с использованием семантических сетей Термин
- 90. Представление знаний с использованием семантических сетей Семантические
- 91. Представление знаний с использованием семантических сетей
- 92. Скачать презентанцию
Классификация по степени использования различных видов знаний В зависимости от того, какие виды знаний используются, и каким образом это происходит, системы искусственного интеллекта можно классифицировать несколькими способами.
Слайды и текст этой презентации
Слайд 31. Если в программной системе используются только фактографические знания, то
такую программную систему называют базой данных (БД) и в современных
условиях обычно не считают содержащей искусственный интеллект.
Слайд 42. Если в программной системе используются главным образом алгоритмические знания,
то такую программную систему принято называть пакетом прикладных программ. Отнесение
такого пакета программ к системе ИИ обычно явно указывается. Если пакет прикладных программ используется просто как библиотека процедур, то его не относят к искусственно-интеллектуальным системам. Если же в нем используются методы ИИ, например, если программу решения конкретной задачи строит не пользователь, а автоматический планировщик, то такой пакет прикладных программ может считаться системой с искусственным интеллектом.
Слайд 53. Если в программной системе в той или иной форме
используются концептуальные знания, то такую систему считают искусственно-интеллектуальной.
Слайд 6Классификация по виду ответа при решении задач
Решая конкретную задачу,
прикладная система ИИ получает на входе знания в той или
иной форме, а на выходе выдает ответ, который также имеет некоторую форму и представляет собой некоторое (новое) знание. В соответствии с введенной классификацией видов знаний искусственно-интеллектуальные системы можно классифицировать по уровню выдаваемого ответа.0. Логический ответ (да или нет); не очень удобны в использовании, сейчас применяются редко.
1. Фактографический ответ (ответ-факт); если выдается конкретный ответ на один вопрос, то такие системы часто называют информационными системами. В настоящее время наиболее распространенный класс систем.
Слайд 72.Процедурный ответ; решая задачу, система может создать и запустить процедуру
(система синтеза программ, автоматическое программирование). Очень интересное и перспективное направление,
привлекающее внимание большого числа исследователей.3. Понятийный ответ; ответ-закон, строится не решение, а схема решения класса задач, может быть даже на компьютере не выполнимая. В настоящее время полномасштабные реализации пока неизвестны.
Слайд 8Приведем примеры ответов разных уровней, используя модельный пример с сортировкой
чисел из параграфа 0 (напомним, задача состоит в следующем: мы
хотим, чтобы компьютер отсортировал набор из трех чисел в порядке их возрастания).(0) 2 5 7 → да
5 2 7 → нет
(1) 5 2 7 → 2 5 7
(2) {x, y, z}?{x < y < z} → Sort3
(3) {xi} отсортировать γ i, j ( i < j → xi < xj )
Слайд 9На уровне 0 мы предъявляем последовательность, а система только проверяет,
отсортирована она или нет. На уровне 1 мы предъявляем последовательность,
и система ее послушно сортирует. На уровне 2 система строит процедуру сортировки, примерно так, как это показано в параграфе 0. Наконец, на уровне 3 гипотетическая система объясняет нам, что это значит — отсортировать массив чисел
Слайд 10ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
В логических моделях знания представляются в виде
совокупности правильно построенных формул какой-либо формальной системы (ФС), которая задается
четверкой:ФС= {T,P,A,R},
где Т— множество базовых (терминальных) элементов, из которых формируются все выражения ФС;
Слайд 11ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Р — множество синтаксических правил, определяющих синтаксически
правильные выражения из терминальных элементов ФС;
А — множество аксиом
ФС, соответствующих синтаксически правильным выражениям, которые в рамках данной ФС априорно считаются истинными; R — конечное множество правил вывода, позволяющих получать из одних синтаксически правильных выражений другие.
Слайд 12ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Простейшей логической моделью является исчисление высказываний.
Высказыванием
называется предложение, смысл которого можно выразить значениями: истина (Т) или
ложь (F). Например, предложения «лебедь белый» и «лебедь чёрный» будут высказываниями.Из простых высказываний можно составить более сложные:
«лебедь белый или лебедь черный»,
«лебеду белый и лебедь черный»,
«если лебедь небелый, то лебедь черный».
Слайд 13ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Логика высказываний оперирует логическими связями между высказываниями,
т. е. она решает вопросы типа: «Можно ли на основе
высказывания А получить высказывание В»; «Истинно ли В при истинности А?» и т.п.Элементарные высказывания рассматриваются как переменные логического типа, над которыми разрешены следующие логические операции:
¬ отрицание (унарная операция);
Слайд 14ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
^ конъюнкция (логическое умножение);
v дизъюнкция (логическое сложение);
→
импликация (если - то);
↔ эквивалентность.
Слайд 16ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Исчисление высказываний позволяет формализовать лишь малую часть
множества рассуждений, поскольку этот аппарат не позволяет учитывать внутреннюю структуру
высказывания, которая существует в естественных языках.
Слайд 17ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
В логике высказываний для обозначения фактов
используются буквы(имена или идентификаторы или фразы), не имеющие структуры (используемые
как атомарные объекты), и принимающие значения "1" или "0" ("да" или "нет"). То, что фразы имеют атомарный характер, не позволяет обнаружить похожесть их смысла. Например, высказывания "расстояние от Земли до Солнца – 150 млрд. км" и "расстояние от Земли до Марса – 60 млн. км" имеют похожий смысл, но абсолютно разные в логике высказываний.
Слайд 18ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Рассмотрим ставший классическим пример рассуждения о Сократе:
Р:
«Все люди смертны»
Q: «Сократ — человек»
R : «Сократ
- смертен»Используя для обозначения высказываний логические переменные Р, Q, R можно составить формулу: (P ^ Q) →R , которая может быть интерпретирована как «Если все люди смертны и Сократ является человеком, то Сократ является смертным».
Слайд 19ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Однако эта формула не является общезначимой, поскольку
относится только к одному объекту (Сократу). Кроме того, высказывание R
не выводится из Р и Q, т.е., если бы мы не сформулировали R заранее, мы не смогли бы записать приведенную выше формулу.
Слайд 20ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Чтобы осуществить этот примитивный логический вывод, высказывание
Q следует разделить на две части: «Сократ» (субъект) и «человек»
(свойство субъекта) и представить в виде отношения «субъект — свойство», которое можно записать с помощью функции человек (Сократ).
Слайд 21ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Очевидно, что свойство конкретного субъекта с именем
«Сократ» быть «человеком» может быть присуще и ряду других субъектов,
что позволяет заменить константу «Сократ» на некоторую переменную, например X. Тогда получим запись человек (X), которая обладает внутренней структурой, т.е. значение такого высказывания будет зависеть от его компонент. Записанная функция уже не является элементарным высказыванием, она называется предикатом.
Слайд 22ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
«Под предикатом будем понимать некоторую связь, которая
задана на наборе из констант или переменных.
Пример предиката: «Р больше
Q».Если семантика P и Q не задана, то о предикате сказать особенно нечего. Но при задании семантики ( т.е. областей определения переменных Р и Q) о предикате можно будет сказать существенно больше.
Слайд 23ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Например, если P и Q - площади
городов в России и Японии, то при задании списков городов
и подстановке значений из этих списков в переменные мы получим отношение между двумя сущностями и сможем судить о его истинности, например:«Площадь Волгограда больше площади Хиросимы» = Т.
«Площадь Вологды больше площади Токио»=F.
Слайд 24ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
В логике предикатов факты обозначаются n-арными логическими
функциями – предикатами F(x1,x2,...,xm), где F – имя предиката (функтор)
и xi – аргументы предиката. Имена предикатов неделимы, т.е. являются так называемыми атомами.
Слайд 25ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Аргументы могут быть атомами или функциями f(x1,x2,...,xm),
где f – имя функции, а x1,...,xm, так же как
и аргументы предикатов являются переменными или константами предметной области. В результате интерпретации предиката функторы и аргументы принимают значения констант из предметной области (строк, чисел, структур и т.д.).
Слайд 26ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Выше приведенные примеры высказываний в виде предикатов
будут выглядеть как "расстояние(Земля, Солнце, 150000000000)" и "расстояние(Земля, Марс, 60000000)".
Так как они имеют определенную структуру, их можно сравнивать по частям, моделируя работу с содержащимся в них смыслом.
Слайд 27ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Предикат с арностью n > 1 может
используется в инженерии знаний для представления n-арного отношения, связывающего между
собой n сущностей (объектов) – аргументов предиката. Например, предикат отец("Иван", "Петр Иванович") может означать, что сущности "Иван" и "Петр Иванович" связаны родственным отношением, а именно, последний является отцом Ивана или наоборот.
Слайд 28ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Предикат "компьютер(память, клавиатура, процессор, монитор)" может обозначать
понятие "компьютер" как отношение, связывающее между собой составные части компьютера,
предикат "внутри(процессор_Pentium, компьютер)" – то, что внутри компьютера находится процессор Pentium.
Слайд 29ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Предикат с арностью n = 1 может
представлять свойство сущности (объекта), обозначенного аргументом или характеристику объекта, обозначенного
именем предиката. Например, кирпичный(дом), оценка(5), улица("Красный проспект"), дата_рождения("1 апреля 1965 г."), быстродействие("1 Мфлопс").Предикат с арностью n = 0 (без аргументов) может обозначать событие, признак или свойство, относящееся ко всей предметной области. Например, "конец работы".
Слайд 31ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
Переменные, находящиеся в сфере действия кванторов, называют
связанными, остальные переменные в логических формулах называются свободными. Для того
чтобы можно было говорить об истинности какого-либо утверждения без подстановки значений в переменные, все входящие в него переменные должны быть связаны кванторами.
Слайд 32ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
К недостаткам логики предикатов как метода представления
знаний можно отнести следующее:
монотонность логического вывода, т.е. невозможность пересмотра полученных
промежуточных результатов (они считаются фактами, а не гипотезами);
Слайд 33ЛОГИЧЕСКАЯ МОДЕЛЬ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ
невозможность применения в качестве параметров предикатов других
предикатов, т.е. невозможность формулирования знаний о знаниях;
детерминированность логического вывода, т.е.
отсутствие возможности оперирования с нечеткими знаниями.Но логику предикатов можно использовать как основу для конструирования более сложных и удобных логических методов представления знаний.
Слайд 35Фреймовая модель
Фреймовая модель представления знаний основана на теории фреймов М.
Минского, которая представляет собой систематизированную психологическую модель памяти человека и
его сознания. Эта теория имеет весьма абстрактный характер, поэтому только на ее основе невозможно создание конкретных языков представления знаний.
Слайд 36Фреймовая модель
В психологии и философии известно понятие абстрактного образа. Например,
слово “ комната” вызывает у слушающих образ комнаты - жилое
помещение с четырьмя стенами, полом, потолком, окнами и дверью. Из этого описания ничего нельзя убрать (например, убрав окна, мы получим уже чулан, а не комнату). Но в нем есть «дырки», или «слоты», - это незаполненные значения некоторых атрибутов - количество окон, цвет стен, высота потолка, покрытие пола и др. Такой образ и называется фреймом . Фреймом называется также и формализованная модель для отображения образа.
Слайд 37Фреймовая модель
ПРИМЕР
Объект "мяч" представляет собой кожаный или резиновый чехол,
наполненный воздухом. Во фрейме "мяч" можно обозначить слоты "радиус" (радиус
оболочки мяча), "спорт" (вид спорта, для которого предназначен мяч), "накачан" (да/нет). Ситуация "лекция" может быть определена как "чтение лектором учебного материала слушателям". Фрейм "лекция" может содержать слоты "предмет" (предмет, по которому проводится лекция), "лектор" (ФИО лектора), "аудитория" (место проведения лекции), "слушатели" (количество слушателей).
Слайд 38Фреймовая модель
Фрейм имеет имя, служащее для идентификации описываемого им понятия,
и содержит ряд описаний — слотов, с помощью которых определяются
основные структурные элементы этого понятия. За слотами следуют шпации, в которые помещают данные, представляющие текущие значения слотов. Слот может содержать не только конкретное значение, но также имя процедуры, позволяющей вычислить это значение по заданному алгоритму.
Слайд 39Фреймовая модель
Например, слот с именем возраст может содержать имя процедуры,
которая вычисляет возраст человека по дате рождения, записанной в другом
слоте, и текущей дате. Процедуры, располагающиеся в слотах, называются связанными или присоединенными процедурами. Вызов связанной процедуры осуществляется при обращении к слоту, в котором она помещена.
Слайд 40Фреймовая модель
В слоте может содержаться не одно, а несколько значений,
т. е. в качестве структурных составляющих фреймов могут использоваться данные
сложных типов, а именно: массивы, списки, множества, фреймы и т. д. Например, в слоте с именем брат может содержаться список имен, если объект, описываемый данным фреймом, имеет нескольких братьев. Значение слота может представлять собой некоторый диапазон или перечень возможных значений, арифметическое выражение, фрагмент текста и т.д.
Слайд 41Фреймовая модель
Совокупность данных предметной области может быть представлена множеством взаимосвязанных
фреймов, образующих единую фреймовую систему, в которой объединяются декларативные и
процедурные знания. Такая система имеет, как правило, иерархическую структуру, в которой фреймы соединены друг с другом с помощью родо-видовых связей. На верхнем уровне иерархий находится фрейм, содержащий наиболее общую информацию, истинную для всех остальных фреймов.
Слайд 42Фреймовая модель
Фреймы обладают способностью наследовать значения характеристик своих родителей. Например,
фрейм АФРИКАНСКИЙ_СЛОН наследует от фрейма СЛОН значение характеристики цвет—«серый». Значение
характеристики в дочернем фрейме может отличаться от родительского, например, значением данного слота для фрейма АЗИАТСКИЙ_СЛОН является цвет=«коричневый».
Слайд 43Фреймовая модель
Существуют 2 типа фреймов – прототипы и экземпляры. Фреймы-прототипы
— это готовые структуры для описания законов. В них отсутствуют
конкретные значения слотов. При заполнении слотов конкретными значениями, они превращаются в конкретные фреймы. Часто в системах фреймы используются для стереотипны последовательностей действий и тогда они называются сушариями. При заполнении фреймов-прототипов, часть слотов может оставаться пустой. Фреймы-экземпляры создаются для отображения реальных ситуацийна основе поступающих данных.
Слайд 44Фреймовая модель
Над фреймами можно совершать некоторые теоретико-множественные операции, например объединение
и пересечение. При объединении фреймов в результирующем фрейме будут присутствовать
все слоты», которые встречались в исходных фреймах. В слотах, не являющихся общими, будут сохранены исходные значения. Если в объединяемых фреймах были одноименные слоты, в результирующем фрейме останется один слот с таким именем, значение его определится в результате объединения значений одноименных слотов.
Слайд 45Фреймовая модель
При пересечении фреймов в результирующем фрейме будут присутствовать только
те слоты, которые имелись во всех исходных фреймах. Вычислить результирующие
значения можно двумя способами. Первый способ состоит в том, что в результирующем фрейме присутствуют только те значения, которые совпадали в исходных фреймах. Во втором способе результирующие значения находят путем пересечения значений из исходных фреймов.
Слайд 47Структура данных фрейма
Имя фрейма. Оно служит для идентификации фрейма
в системе и должно быть уникальным. Фрейм представляет собой совокупность
слотов, число которых может быть произвольным. Число слотов в каждом фрейме устанавливается проектировщиком системы, при этом часть слотов определяется самой системой для выполнения специфических функций (системные слоты), примерами которых являются: слот-указатель родителя данного фрейма, слот-указатель дочерних фреймов, слот для ввода имени пользователя, слот для ввода даты определения фрейма, слот для ввода даты изменения фрейма и т.д.
Слайд 48Структура данных фрейма
Имя слота. Оно должно быть уникальным в пределах
фрейма. Обычно имя слота представляет собой идентификатор, который наделен определенной
семантикой. В качестве имени слота может выступать произвольный текст.Например, <Имя слота>= Главный герой романа Ф. М. Достоевского «Идиот», <Значение слота>= Князь Мышкин. Имена системных слотов обычно зарезервированы, в различных системах они могут иметь различные значения. Системные слоты служат для редактирования базы знаний и управления выводом во фреймовой системе.
Слайд 49Структура данных фрейма
Указатели наследования.
Они показывают, какую информацию об атрибутах
слотов из фрейма верхнего уровня наследуют слоты с аналогичными именами
в данном фрейме. Указатели наследования характерны для фреймовых систем иерархического типа, основанных на отношениях типа «абстрактное — конкретное».В конкретных системах указатели наследования могут быть организованы различными способами и иметь разные обозначения:
Слайд 50Структура данных фрейма
U (Unique) — значение слота не наследуется;
S (Same)
- значение слота наследуется;
R (Range) - значения слота должны находиться
в пределах интервала значений, указанных в одноименном слоте родительского фрейма;О (Override) — при отсутствии значения в текущем слоте оно наследуется из фрейма верхнего уровня, однако в случае определения значения текущего слота оно может быть уникальным. Этот тип указателя выполняет одновременно функции указателей U и S.
Слайд 51Структура данных фрейма
Указатель типа данных. Он показывает тип значения слота.
Наиболее употребляемые типы: frame — указатель на фрейм; real —
вещественное число; integer — целое число; boolean — логический тип; text — фрагмент текста; list — список; table — таблица; expression — выражение; lisp - связанная процедура и т.д.
Слайд 52Структура данных фрейма
Демоны.
Демоном называется процедура, автоматически запускаемая при выполнении
некоторого условия. Демоны автоматически запускаются при обращении к соответствующему слоту.
Типы демонов связаны с условием запуска процедуры.
Слайд 53Структура данных фрейма
Демон с условием IF-NEEDED запускается, если в момент
обращения к слоту его значение не было установлено. Демон типа
IF-ADDED запускается при попытке изменения значения слота. Демон IP-REMOVED запускается при попытке удаления значения слота. Возможны также другие типы демонов. Демон является разновидностью связанной процедуры.
Слайд 54Структура данных фрейма
Присоединенная процедура запускается по сообщению, переданному из другого
фрейма. Демоны и присоединенные процедуры являются процедурными знаниями, объединенными вместе
с декларативными в единую систему. Эти процедурные знания являются средствами управления выводом во фреймовых системах, причем с их помощью можно реализовать любой механизм вывода.
Слайд 56Структура фрейма «Научная конференция»
Демон ЗАКАЗ — это процедура, которая автоматически
запускается при попытке подстановки значения в слот с именем Место
проведения. Ее главное назначение состоит в проверке возможности заказа аудитории на нужное время.
Слайд 57Структура фрейма «Научная конференция»
Демон КТО? автоматически запускается при обращении к
слоту Докладчик, если значение этого слота не определено. Основное содержание
данной процедуры — генерация запроса к пользователю типа «Кто выступает?», получение ответа и его запись в качестве значения слота.
Слайд 61Пример сети фреймов
Понятие УЧЕНИК наследует свойства фреймов РЕБЕНОК и
ЧЕЛОВЕК, которые находятся на более высоких уровнях иерархии. Если будет
задан вопрос «Любят ли ученики сладкое?», то следует ответ “да», так как этим свойством обладают все дети, что указано во фрейме РЕБЕНОК. Наследование свойств может быть частичным, например «возраст» для учеников не наследуется из фрейма «ребенок», так как явно указан в собственном фрейме.
Слайд 62Пример сети фреймов
Понятие УЧЕНИК наследует свойства фреймов РЕБЕНОК и
ЧЕЛОВЕК, которые находятся на более высоких уровнях иерархии. Если будет
задан вопрос «Любят ли ученики сладкое?», то следует ответ “да», так как этим свойством обладают все дети, что указано во фрейме РЕБЕНОК. Наследование свойств может быть частичным, например «возраст» для учеников не наследуется из фрейма «ребенок», так как явно указан в собственном фрейме.
Слайд 63Фреймовая модель
Модель фрейма является достаточно универсальной, поскольку
позволяет отобразить все
многообразие знаний о мире через:
фреймы - структуры для обозначений объектов
и понятий;фреймы - роли;
фреймы – сценарии;
фреймы – ситуации.
Слайд 64Фреймовая модель
Пример.
Фрейм-структурами являются понятия "заем", "вексель","кредит".
Фрейм-роли -
"кассир", "клиент", "сервер". Фрейм-сценарии -"страхование", "банкинг", "банкротство".
Фрейм-ситуации - "эволюция",
"функционирование", "безработица".
Слайд 65Реализация фреймовой модели представления знаний на примере решения задачи Эйнштейна
Условия
задачи следующие:
1. Есть пять домов, каждый разного цвета.
2. В каждом
доме живет один человек, отличающий;ся от соседнего по национальности: немец, англи;
чанин, швед, датчанин, норвежец.
3. Каждый пьет только один напиток, выращивает
определенное растение и держит определенное
животное.
4. Никто из 5 человек не пьет одинаковые с другими
напитки, не выращивает одинаковое растение и
не держит одинаковое животное.
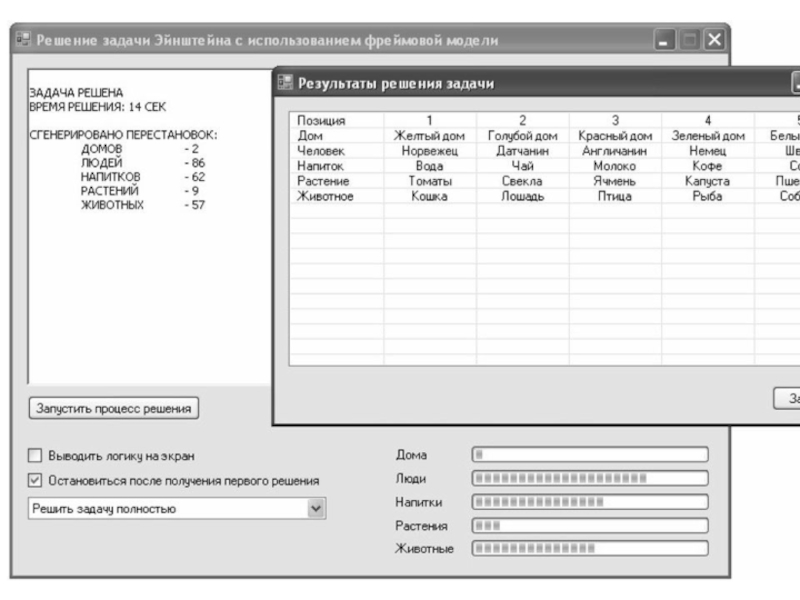
Слайд 66Цель решения: определить, кому принадлежит
рыба?
При этом дополнительные условия включают
следующее:
1.
Англичанин живет в красном доме.
2. Швед держит собаку.
3. Датчанин пьет
чай.4. Зеленый дом стоит слева от белого.
5. Жилец зеленого дома пьет кофе.
6. Человек, который выращивает ячмень, держит
птицу.
7. Жилец из среднего дома пьет молоко.
8. Жилец из желтого дома выращивает томаты.
Слайд 679.Норвежец живет в первом доме.
10.Тот, кто держит кошку, живет около
того, кто вы;
ращивает свеклу.
11.Человек, который содержит лошадь, живет около
того, кто
выращивает томаты.12.Тот, кто выращивает пшеницу, пьет сок.
13.Норвежец живет около голубого дома.
14.Немец выращивает капусту.
15.Тот, кто выращивает свеклу, живет по соседству с человеком, который пьет воду.
Слайд 68Если трактовать условие (4) как «зеленый дом
стоит непосредственно слева от
белого», то задача имеет единственное решение. Причем под решением в
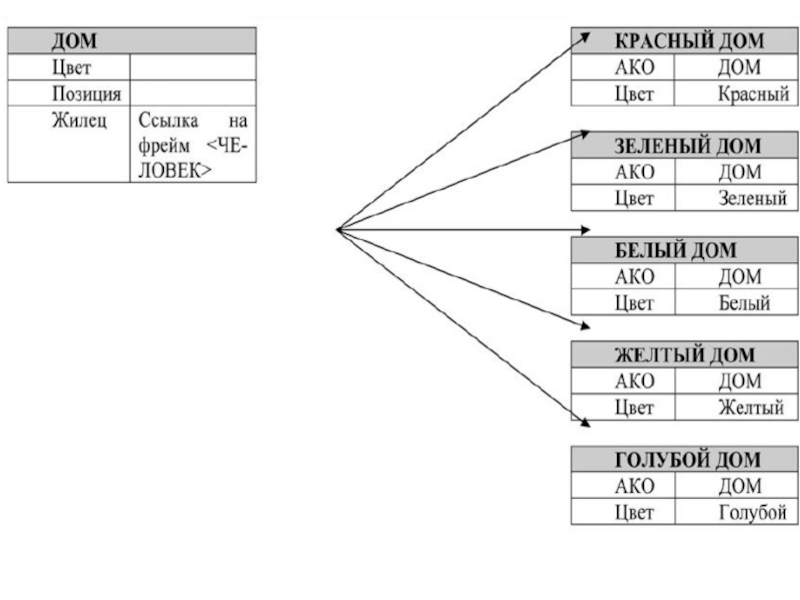
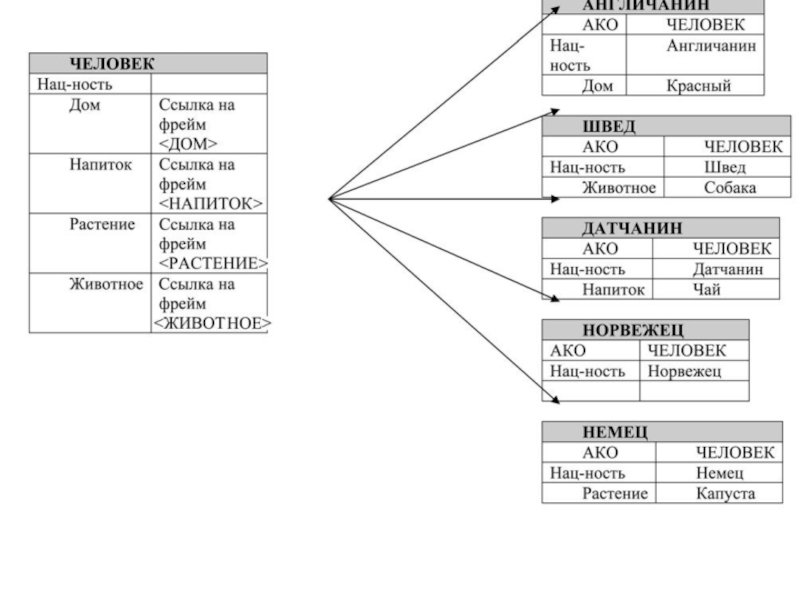
данном случае понимается не только определение того, кому принадлежит рыба, но и полное распределение: дом – человек – напиток – растение – животное, охватывающее все объекты, описанные в условии.
Слайд 69Попробуем представить предметную область
задачи с помощью набора фреймов. В условии
фигурируют объекты 5 классов: «дом», «человек», «напиток», «растение» и «животное».
Каждому классу принадлежит 5 объектов. Таким образом, наиболее логичным решением в данном случае будет создание для каждого класса абстрактного фрейма, описывающего этот класс, а для каждого объекта, принадлежащего классу, создание конкретного фрейма, наследуемого от абстрактного и описывающего этот объект.
Слайд 70На рис. 1 представлены фреймовые диаграммы классов «Дом» и «Человек».
Диаграммы классов «Напиток», «Растение» и «Животное» не показаны, поскольк представляющие
их фреймы достаточно тривиальны (не содержат ни одного слота).Диаграмма показывает, что фреймы, представляющие конкретные объекты, наследуют слоты абстрактных фреймов, определяя значения для некоторых из них. Таким образом, часть информации, содержащейся в условии задачи, задается с помощью значений слотов. Данная информация носит декларативный характер, поскольку задается на этапе построения модели и не требует дополнительных проверок.
Слайд 73Другая часть информации может быть заложена в
модель с помощью процедур,
задаваемых для фрейма и вызываемых при изменении значения его слотов.
Эта
информация носит характер проверяемых условий. Например, условие «жилец желтого дома выращивает томаты» может быть проверено процедурой, вызываемой при изменении значения слота «РАСТЕНИЕ» фрейма «ЖЕЛТЫЙ ДОМ».
Слайд 74Сложнее обстоит дело с условиями типа «тот, кто держит кошку,
живет около того, кто выращивает свеклу». Для проверки таких условий
каждый дом должен располагать информацией о соседних домах и их обитателях.В программе, которая будет рассмотрена ниже, связь домов друг с другом реализована путем введения списка домов, учитывающего их расстановку, причем каждый «дом» имеет доступ к этому списку.
Слайд 75Фреймовая модель очень удобна с точки зрения программной реализации, поскольку
она напрямую соответствует парадигме объектно- ориентированного программирования (ООП). С точки
зрения ООП, фреймы представляют собой ничто иное, как классы.Слоты являются аналогом полей классов. Иерархия
фреймов соответствует иерархии классов, которая
строится с помощью механизма наследования. Про
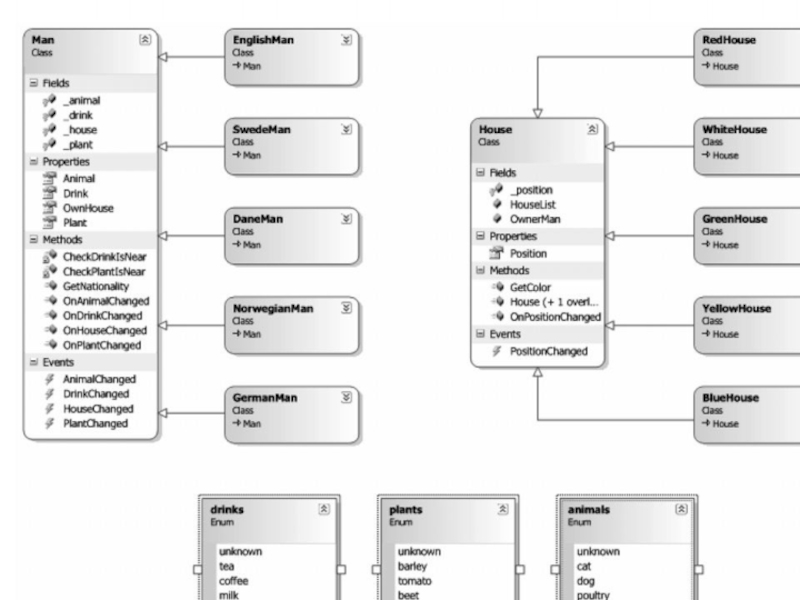
Слайд 76На рис. 2 представлена диаграмма классов, реализующих фреймовую модель предметной
области (далее просто «Модель»). Ключевыми являются классы «House» и «Man»,
от которыхнаследуются классы, описывающие уже конкретные
дома и конкретных людей. Программный модуль состоит из двух основных
частей: набора классов, реализующих фреймовую
модель, и внешнего модуля, который осуществляет
генерацию наборов данных, наблюдение за «реакци;
ей» модели и принятие необходимых решений.
Слайд 78Вся предметная область разбита на пять уровней:
1) уровень домов →
2) уровень людей → 3) уровень напитков → 4) уровень
растений → 5) уровень животных.Такой порядок следования уровней означает, что сначала определяется позиция дома, затем для данного дома определяется его жилец, после чего для жильца определяются его напиток, растение и животное. В общем случае порядок уровней не играет решающей роли, но для конкретной реализации он должен быть фиксирован.
Слайд 79Программа действует методом проб и ошибок. На самом верхнем уровне
генерируется перестановка домов. Каждому дому присваивается позиция, соответствующая его номеру
в перестановке. При этом программа наблюдает за «реакцией» модели. Допустим, что в перестановке зеленый дом оказался справа от белого (по условию, зеленый дом стоит слева от белого). При присвоении зеленому дому его позиции он проверит, где в дан ный момент находится белый дом.
Слайд 80Если позиция белого дома уже определена, и он не стоит
слева от зеленого, объект, представляющий зеленый дом, выбросит исключение, сигнализирующее
о том, что произошел конфликт с условием задачи. Внешняя программа перехватит исключение, произведет откат перестановки на текущем уровне (обнулит позиции всех домов) и перейдет к генерации следующей перестановки. Если же текущая перестановка не вызвала конфликт условий, программа спустится на уровень ниже.
Слайд 81На следующем уровне генерируется перестановка людей. После генерации каждому человеку
присваивается
дом из текущей перестановки домов,
номер которого соответствует номеру данного чело;
века
в перестановке людей. При этом модель автоматически присваивает значения определенным атрибутам объектов в соответствии с условиями задачи.Допустим, внешняя программа пытается «поселить»
датчанина в желтый дом, стоящий на позиции «3».
Объект, представляющий датчанина, проверяет по;
Слайд 82зицию желтого дома и, обнаружив, что дом стоит посередине, присваивает
атрибуту «напиток» значение «молоко», т.к. по условию жилец из среднего
дома пьет молоко. При этом этот же объект проверяет, не связано ли молоко с каким-либо другим человеком.Если оказывается, что молоко уже используется для кого-то в качестве напитка, генерируется исключение. Таким образом, модель самостоятельно проверяет соблюдение всех условий задачи. Внешней программе остается лишь генерировать перестановки и следить за реакцией модели.
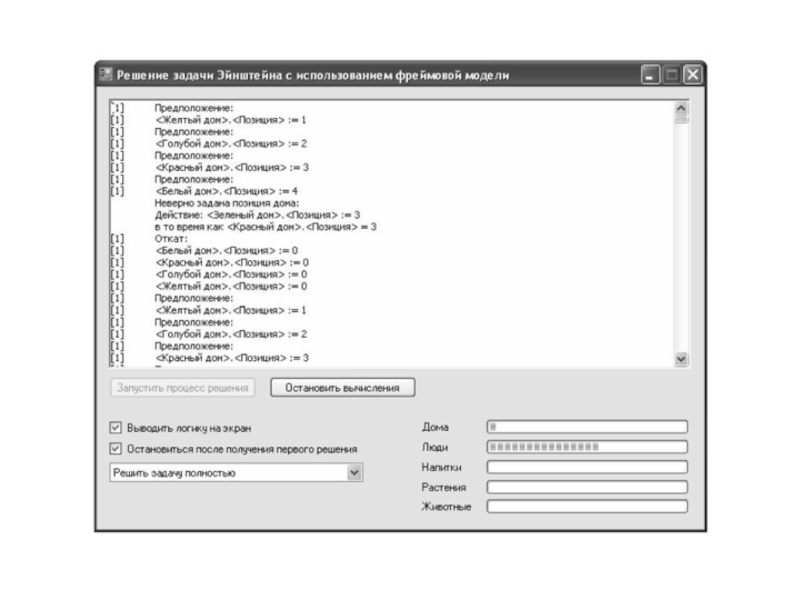
Слайд 83На рис. 3 показана работа программы в процессе решения задачи.
Имеется возможность вывести на консоль ход «рассуждений» программы. При этом,
как уже было сказано, предположения относительно расположения и принадлежности объектов делаются внешней программой, а проверка условий и генерация исключений (включая формирование текста ошибки) осуществляются моделью.
Слайд 86Фреймовая модель
Основные преимущества фреймов как модели представления знаний является
способность отражать концептуальную основу организации памяти человека, а также естественность,
наглядность представления, модульность, поддержку возможности использования правил умолчания, приписываемых слотам. Однако фрейм - представление является не конкретным языком представления знаний, а некоторой идеологической концепцией, реализуемой по-разному в различных языках.
Слайд 87Фреймовая модель
Теория фреймов послужила толчком к разработке нескольких языков
представления знаний, которые благодаря своим широким возможностям и гибкости стали
в последние годы довольно распространенными языками. К ним относятся FRL (Frame RepresentationLanguage), KRL, FMS и др., представляющие собой среду для разработок и исследований в области ИИ и широко используемые специалистами в данной области.
Слайд 88Фреймовая модель
Теория фреймов послужила толчком к разработке нескольких языков
представления знаний, которые благодаря своим широким возможностям и гибкости стали
в последние годы довольно распространенными языками. К ним относятся FRL (Frame RepresentationLanguage), KRL, FMS и др., представляющие собой среду для разработок и исследований в области ИИ и широко используемые специалистами в данной области.
Слайд 89Представление знаний с использованием семантических сетей
Термин семантическая сеть применяется для
описания метода представления знаний, основанного на сетевой структуре. Семантические сети
были первоначально разработаны для использования их в качестве психологических моделей человеческой памяти, но теперь это стандартный метод представления знаний в ИИ и в экспертных системах.
Слайд 90Представление знаний с использованием семантических сетей
Семантические сети состоят из точек,
называемых узлами, и связывающих их дуг, описывающих отношения между узлами.
Узлы в семантической сети соответствуют объектам, концепциям или событиям. Дуги могут быть определены разными методами, зависящими от вида представляемых знаний. Обычно дуги, используемые для представления иерархии, включают дуги типа isa (является) и has-part (имеет часть).
