Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделі та моделювання
Содержание
- 1. Моделі та моделювання
- 2. Моделі та моделюванняМодель – деякий об'єкт, процес,
- 3. Види подоб:1. Точна подоба – подоба між
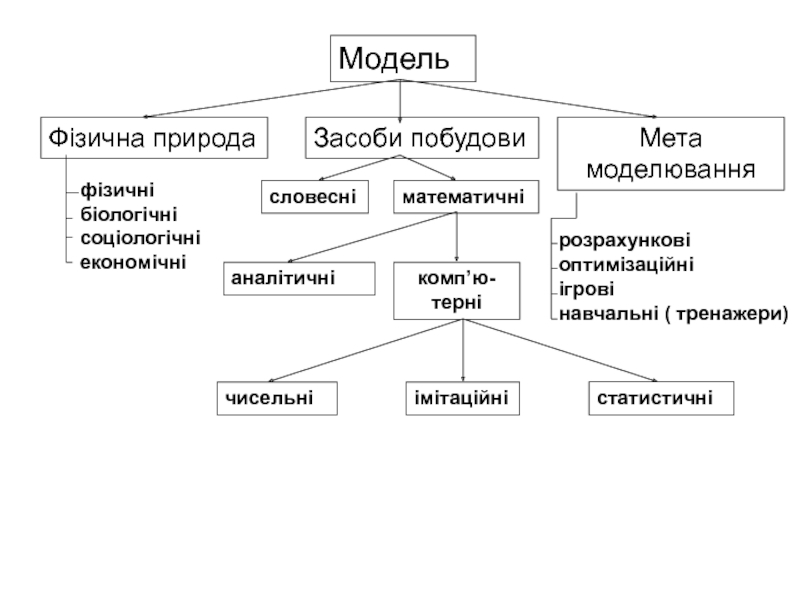
- 4. МодельФізична природаЗасоби побудовиМета моделюванняфізичні біологічні соціологічні економічні розрахункові оптимізаційні ігрові навчальні ( тренажери)словесніматематичніаналітичнікомп’ю-тернічисельніімітаційністатистичні
- 5. 3. Етапи моделювання та принципи побудови математичних
- 6. Основні етапи ІМ 1. Постановка завдання. 2.
- 7. 4. Оцінка адекватності моделей.
- 8. Скачать презентанцию
Моделі та моделюванняМодель – деякий об'єкт, процес, система, знакове утворення, що перебуває відносно подоби до досліджуваного об'єкта.Моделювання – дослідження на моделі, що подібна до об'єкта.Подоба - взаємооднозначна відповідність між двома об'єктами
Слайды и текст этой презентации
Слайд 1Тема: “Поняття про моделі та моделювання“
Моделі та моделювання.
Класифікація моделей.
Етапи моделювання
та принципи побудови математичних моделей.
Слайд 2Моделі та моделювання
Модель – деякий об'єкт, процес, система, знакове утворення,
що перебуває відносно подоби до досліджуваного об'єкта.
Моделювання – дослідження на
моделі, що подібна до об'єкта.Подоба - взаємооднозначна відповідність між двома об'єктами або системами, при якій функції, що характеризують перехід від одних параметрів до інших, відомі, а між математичними описами цих об'єктів установлені тотожні відносини.
Слайд 3Види подоб:
1. Точна подоба – подоба між всіма елементами досліджуваного
об'єкта й моделі. Така подоба називається подобою з точністю до
ізоморфізму.2. Наближена подоба - подоба, що допускає порушення взаємооднозначної відповідності між об'єктом і моделлю, порушення процесів, що протікають у моделі при порівнянні з досліджуваним об'єктом може бути оцінене аналітично або експериментально.
3. Фізична подоба - подоба між досліджуваним об'єктом і моделлю, які мають ту саму фізичну природу.
4. Структурна подоба - подоба структур досліджуваного об'єкта й моделі.
5. Функціональна подоба - подоба функцій, які виконуються досліджуваним об'єктом і моделлю при тих самих вхідних сигналах.
6. Математична подоба - подоба між величинами, які входять у математичний опис досліджуваного об'єкта й моделі при тих самих вхідних сигналах.
7. Динамічна подоба - подоба між послідовними станами досліджуваного об'єкта й моделі.
8. Імовірнісна подоба - подоба між імовірнісними характеристиками досліджуваного об'єкта й моделі.
9. Геометрична подоба - подоба між просторовими характеристиками досліджуваного об'єкта й моделі.
Моделювання як метод системного аналізу
Однією з проблем при проведенні системного аналізу, є проблема експерименту в системі або над системою. Це суцільно пов'язане з матеріальними витратами й (або) значними втратами інформації.
Досвід людської діяльності вчить — треба експериментувати не над об'єктом, предметом або системою, а над їхніми моделями, тобто копією об'єкта в зменшеному або збільшеному вигляді.
Слайд 4Модель
Фізична природа
Засоби побудови
Мета моделювання
фізичні
біологічні
соціологічні
економічні
розрахункові оптимізаційні
ігрові
навчальні ( тренажери)
словесні
математичні
аналітичні
комп’ю-терні
чисельні
імітаційні
статистичні
Слайд 53. Етапи моделювання та принципи побудови математичних моделей.
Процес дослідження включає
наступні основні етапи.
Постановка задачі.
Побудова математичної моделі.
Знаходження рішення за допомогою моделі.
Послямодельний
аналіз та коректування отриманого результату.Побудова математичної моделі вимагає:
виділення об’єкта, що розглядається; відкидання всього несуттєвого і уяснення всього суттєвого;
точного кількісного опису ситуації для того щоб цей опис можна було б перевести на математичний язик;
визначення набору параметрів, що характеризують як стан системи, так і можливе управління системою;
визначення залежності між параметрами стану і управління;
визначення цілі через параметри системи в термінах відповідної математичної моделі.
Математична модель установлює відповідність між значеннями управляємих і неуправляємих змінних і знаходить результати рішення.
В загальному вигляді математична модель може бути представлена :
, (1)
де – критерій ефективності,
– управляємі змінні,
– неуправляємі змінні або випадкові впливи,
– функції, що виражають обмеження.
Зазвичай мова іде про знаходження оптимуму критерію ефективності при дотримуванні даних обмежень.
Слайд 6
Основні етапи ІМ
1. Постановка завдання.
2. Формування й побудова
концептуальної моделі (КМ).
3. Побудова ІМ.
4. Оцінка адекватності ІМ.
5. Планування
експерименту.6. Модельний експеримент (накопичення й статистична обробка результатів моделювання).
7. Інтерпретація результатів модельного експерименту.
Слайд 7 4. Оцінка адекватності моделей.
Вибір
методу рішення залежить від виду моделі. Існує чотири типа методів
знаходження рішення: аналітичний, чисельний, статистичних досліджень і евристичний. Оскільки модель не може бути точним відображенням реальності, отримане рішення може виявитися неприйнятним для умов конкретної ситуації. Тому необхідний аналіз отриманого в результаті моделювання рішення, який полягає в перевірці адекватності моделі, а також в коректуванні рішення.Порушення адекватності відображення моделлю реальності може відбутися по наступним причинам.
1. Модель може неправильно відображати дійсну залежність, яка існує між результатом операції і змінними.
2. У моделі можуть не враховуватися змінні, які впливають на результат.
3. Значення змінних, що входять в модель, можуть бути оцінені неправильно.
Аналіз результатів моделювання здійснюється для установлення адекватності відображення моделлю реальності, а в випадку її порушення — виявлення причин порушення і відповідної зміни моделі.
Критерії ефективності як міра успішності рішення задач.
Вибір критерію ефективності є найбільш відповідальним етапом всієї постановки задачі. Основною вимогою до критерію ефективності є установлення строгої відповідності між ним и кінцевою ціллю.
Якщо розглядати застосування критеріїв ефективності для оптимізації, то в загальному вигляді оптимізація зводиться до знаходження рішень, що відповідають максимальному значенню чисельного вираження вибраного критерію ефективності.